Задача №1

Условие: вычислить значение функции при y[-1;1] с шагом ∆y = 0,1

Решение:

· в ячейку А1 введем y

· в ячейку В1 введем t

· в ячейку С1 введем x

· в ячейку А2 введем начальное значение аргумента у из нашего отрезка, равное -1.

· Выбираем команду ПравкаЗаполнитьПрогрессия и в появившемся диалоговом окне Прогрессия в группе Расположение устанавливаем по столбцам, а в группе Тип – в положение Арифметическая. В поле Шаг вводим значение нашего шага 0.1 , а поле Предельное значение 1 и жмем ОК, после чего будет выполнено построение прогрессии.

· Можно ввести значение у и другим способом: появившемся диалоговом окне Пппр в ячейки А2 и А3 вводим -1 и -0.9 , выделяем эти ячейки, наводим стрелку мыши на черный квадратик в правом нижнем углу до появления черного крестика (маркера заполнения) и протягиваем его вниз до значения у =1,то есть до ячейки А22)

· в ячейку В2 введем формулу: заходим ВставкаФункциякатегория Логические выбираем функцию ЕслиОК появляется окно Аргументы функции.

В поле Лог выражение вводим А2>=0

В поле Значение если истина (1+А2^2)^(1/2)

В поле Значение если ложь1ОК. Получили значение t(=1) при у = -1

· выделяем В2 до появления черного крестика, и протягиваем до В22. Получили значения аргумента t при соответствующих значениях у

· аналогично вычисляем и значение х. В ячейку С2 вводим формулу: ВставкаФункциякатегория Логические выбираем функцию Если ОК

В поле Лог выражение вводим А2>B2

В поле Значение если истина SIN(A2-B2)

В поле Значение если ложь EXP(-A2)+1/(B2^2)ОК. Получили значение x (=3.71828) при t =1

· выделяем C2 до появления черного крестика, и протягиваем до C22. Получили значения аргумента x при соответствующих значениях t

· таблица сделана.

Задача №2

матрица диаграмма уравнение функция

Условие: найти максимальное значение элементов каждого ряда матрицы А и минимальное значение элементов каждого столбца матрицы В

Решение:

· вводим в ячейки А2-D5 входные данные нашей матрицы А, а в G2-J5 матрицы В

· выделяем ячейку Е2, в которую будем помещать результат: заходим ВставкаФункциякатегория Статистические выбираем функцию МАКС ОК появляется окно Аргументы функции.

В поле Число1 устанавливаем курсор и выделяем мышкой диапазон А2-D2, то есть строку матрицы А ОК

Полученный результат протягиваем до Е5 .Мы нашли максимальное значение элементов каждого ряда матрицы А

· выделяем ячейку G7, в которую будем помещать результат: заходим ВставкаФункциякатегория Статистические выбираем функцию МИН ОК появляется окно Аргументы функции.

В поле Число1 устанавливаем курсор и выделяем мышкой диапазон G2-G5, то есть столбец матрицы ВОК

·полученный результат протягиваем до G7. Мы нашли минимальное значение элементов каждого столбца матрицы В

Задача №3

Условие: построить поверхность 25x + 4y – 6z = - 1, при X,Y [-1; 1]

Дано: X,Y

Найти: Z

Решение:

·из нашего уравнения вычислим Z, z =

·в диапазон ячеек B1-L1 вводим последовательные значения переменной х: -1;-0.8 ; …; 1 ( можно через Прогрессию или с помощью маркера заполнения )

·в диапазон ячеек А1-А12 вводим последовательные значения переменной у: -1;-0.8 ; …; 1

·в ячейку В2 введем формулу: =((25*$A2^2+4*B$1^2+1)/6)^(1/2)Enter (=2,236…)

·выделяем ячейку В2, устанавливаем курсор мыши на ее маркере заполнения и протягиваем так, чтобы заполнить диапазон B2 – L12

Знак $ , который стоит перед буквой в имени ячейки, дает абсолютное посылание на столбик с данным именем ;

Знак $ , который стоит перед цифрой - абсолютное посылание на ряд с обозначенным именем

Построим поверхность:

· выделяем диапазон ячеек А1-L12 , включаем Мастер диаграмм и выбираем – Поверхность вид-1 в строках добавить легенду Готово.

Задача №4

Условие: найти один из корней нелинейного уравнения sin ( ln x ) – cos( ln x ) +2 ln x =0

Найти: X

Решение:

для нахождения корней нелинейного уравнения мы изначально построим график функции на отрезке [0.2; 2] с шагом 0,2 , так как нам нужны положительные действительные (вещественные) числа, для которых вычисляется натуральный логарифм ( т.е. х>0, х0 )

· в ячейку А1 введем нахождение корней уравнения

· в А2 х

· в В2 у

· в А3 – А13 0.2 , 0.4 , 0.6 ,……2 ( можно через Прогрессию или с помощью маркера заполнения )

· в ячейку В3 введем формулу: = SIN (LN (A3)) – COS(LN(A3)) + 2*LN(A3) Enter

· заполним столбик значений функции

· выделяем диапазон ячеек А2 – В13 и строим график :

-вызываем Мастер диаграмм и в открывшемся окне выбираем График ( График с маркерами , помечающими точки данных ) Далее

- в Диапазоне данных устанавливаем в столбцах ;

- Ряд У ( Имя : выделить ячейку В2 ; Значения : В3-В13 ; Подписи оси Х : А2 – А13 ) Далее

- ставим галочку в Добавить легенду ( справа ) Далее Готово

· приблизительные значения корней уравнения находятся в точках пересечения графика с осью Х :

- для этого устанавливаем курсор мыши на точку пересечения ( у нас она одна )

- появились координаты ( Ряд "у" Точка " 1,38" Значение 0,01213265 )

· в ячейку С3 вводим наше приближенное значение корня 1,38

· копируем содержание ячейки В3 в ячейку D3 ( получаем то же значение 0,012133 )

· увеличим предельное число итераций и уменьшим относительную погрешность :

- выделяем ячейку D3

- заходим в Сервис Параметры вкладыш Вычисления

- в поле Предельное число вводим 1000

- в поле Относительная погрешность 0,00001 ОК

- снова заходим в Сервис Подбор параметра

в поле Установить в ячейке : будет ячейка D3

в поле Значение : введем 0

в поле Изменяя значение : введем С3 ( или просто выделим ячейку С3 )

ОК

· получили точное значение корня нелинейного уравнения sin ( ln x ) – cos( ln x ) +2 ln x =0

Задача №5

Условие: для каждой из теоретических зависимостей

y = c₁ + c₂ x , y = c₁ + c₂ x + c₃ x² , y = ae^bx

найти значения параметров и выбрать зависимость, которая наилучшим образом представляет функцию заданную таблицею

Решение:

· вводим в диапазон ячеек В1 – К2 табличные данные и выделяем их

· вызываем Мастер диаграмм и выбираем тип Точечная ( Вид первый ) Далее

- Диапазон данных в строках Далее

- во вкладыше Легенда убираем галочку из Добавить легенду Далее ОК

- выделяем курсором мыши область построения диаграммы и с основного меню выбираем команду Диаграмма Добавить линию тренда Тип Линейная , во вкладыше Параметры выбираем показывать уравнение на диаграмме ОК

· аналогично строим линии тренда Полиномиальную и Экспоненциальную. Можно иначе: копируем Линейную диаграмму 2 раза и выделяем первую копию, клацаем правой клавишей мыши Добавить линию тренда меняем на Полиномиальную; вторую копию меняем на Экспоненциальную; лишнее удаляем

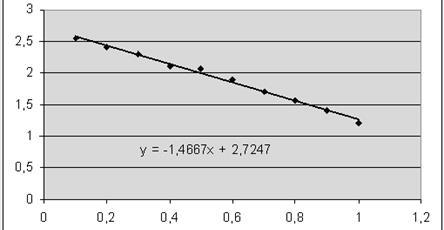
Линейная ( у₁ )

Полиномиальная ( у₂ )

Экспоненциальная (у₃ )

вычислим значения функций у_{1 ,} у_{2 ,} у₃ в заданных точках , где у_{1 ,} у_{2 ,} у₃ – уравнения Линейной, Полиномиальной и Экспоненциальной линий тренда соответственно:

- в ячейку В4 вводим формулу = - 1,4667*В1+ 2,7247 ( получаем 2,578 ) Enter и размножаем в ячейки В4 – К4 с помощью маркера заполнения

- в ячейку В5 вводим формулу = -0,3561*В1^2 – 1,075*В1+2,6463 Enter и размножаем в ячейки В5 – К5

- в ячейку В6 вводим формулу = 2,9003*ЕХР(-0,7994*В1) Enter и размножаем в ячейки В6 – К6

· найдем такую зависимость , при которой величина S_i = будет минимальною , где i , j - количество исследоваемых теоретических зависимостей . Для этого вычислим значения ( у - у):

- в ячейку В8 вводим формулу =( В4 – В2 )^2 ( получаем 0,0008 ) Enter и размножаем в ячейки В8 – К8

- в ячейку В9 вводим формулу =( В5 – В2 )^2 ( получаем 0,0002 ) Enter и размножаем в ячейки В9 – К9

- в ячейку В10 вводим формулу =( В6 – В2 )^2 ( получаем 0,0162 ) Enter и размножаем в ячейки В10 – К10

Можно иначе : введем в ячейку В8 формулу =( В4 – В$2 )^2 Enter и размножаем в ячейки В8 – К10 , так как знак $ , который стоит перед цифрой - дает абсолютное посылание на ряд с обозначенным именем

· в ячейке В12 вычисляем S₁ :

- заходим ВставкаФункциякатегория Математические выбираем

Функцию СУММ ОК появляется окно Аргументы функции.

- в поле Число1 устанавливаем курсор и выделяем мышкой диапазон В8-К8

ОК (0,0123)

· аналогично вычисляем S₂ (0,0056), S₃ (0,0559)

Можно иначе: после того, как вычислили S₁ (с помощью маркера заполнения) размножаем в ячейки В12 – В14

· выделяем ячейки В12 – В14 заходим Формат Ячейки … Число Процентный (число десятичных знаков) ОК. Получаем 1,23% , 0,56% , 5,59%

· самый наименьший процент у Полиномиальной функции , то есть она наиболее приближенна к нашим табличным данным