| Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет им. Ф. Скорины»
Математический факультет
Курсовая работа
О МИНИМАЛЬНЫХ  -ЗАМКНУТЫХ ТОТАЛЬНО НАСЫЩЕННЫХ НЕ -ЗАМКНУТЫХ ТОТАЛЬНО НАСЫЩЕННЫХ НЕ  -ФОРМАЦИЯХ КОНЕЧНЫХ ГРУПП -ФОРМАЦИЯХ КОНЕЧНЫХ ГРУПП
Исполнитель:
Студентка группы М-32 Макаренко Л.А.
Научный руководитель:
Канд. физ-мат. наук, доцент Сафонов В.Г.
Гомель 2006
Содержание
Введение
1. Определения и обозначения
2. Используемые результаты
3. Основные результаты
Заключение
Литература
Введение
Все рассматриваемые в работе группы предполагаются конечными. Используемую терминологию можно найти в [1, 2].
При изучении внутреннего строения, а также классификации насыщенных формаций важную роль играют так называемые минимальные насыщенные не  -формации [3] или -формации [3] или 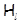 -критические формации [4]. Напомним, что насыщенная формация -критические формации [4]. Напомним, что насыщенная формация  , называется минимальной насыщенной не , называется минимальной насыщенной не  -формацией, если все собственные насыщенные подформации -формацией, если все собственные насыщенные подформации 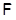 содержатся в классе групп содержатся в классе групп  . Задача изучения формаций такого рода впервые была поставлена Л.А. Шеметковым на VI симпозиуме по теории групп [3]. Ее решение, в классе насыщенных формаций, получено А.Н. Скибой [5]. . Задача изучения формаций такого рода впервые была поставлена Л.А. Шеметковым на VI симпозиуме по теории групп [3]. Ее решение, в классе насыщенных формаций, получено А.Н. Скибой [5].
В теории тотально насыщенных формаций изучение минимальных тотально насыщенных не  -формаций было начато А.Н.Скибой в книге [2], где было дано описание разрешимых минимальных тотально насыщенных не -формаций было начато А.Н.Скибой в книге [2], где было дано описание разрешимых минимальных тотально насыщенных не 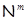 -формаций ( -формаций (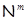 – формация всех разрешимых групп нильпотентной длины – формация всех разрешимых групп нильпотентной длины  ). В работах автора [6-10] теория минимальных ). В работах автора [6-10] теория минимальных  -замкнутых тотально насыщенных не -замкнутых тотально насыщенных не  -формаций получила свое дальнейшее развитие. Основными результатами в этом направлении являются следующие теоремы. -формаций получила свое дальнейшее развитие. Основными результатами в этом направлении являются следующие теоремы.
Теорема 1 [10].
Пусть 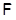 и и  – –  -замкнутые тотально насыщенные формации, -замкнутые тотально насыщенные формации,  . Тогда и только тогда . Тогда и только тогда 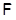 – минимальная
– минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -формация, когда -формация, когда
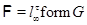 , где , где 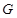 – такая монолитическая – такая монолитическая  -минимальная не -минимальная не  -группа с монолитом -группа с монолитом 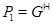 , что выполняется одно из следующих условий: , что выполняется одно из следующих условий:
1) 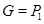 – группа простого порядка – группа простого порядка 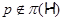 ; ;
2) 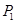 – неабелева группа и – неабелева группа и  , где , где 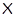 – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы 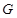 ; ;
3) 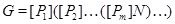 , ,
где 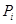 – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в 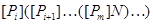 при всех при всех 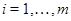 , а , а 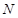 либо группа простого порядка либо группа простого порядка  , либо такая монолитическая , либо такая монолитическая  -минимальная не -минимальная не 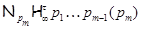 -группа с неабелевым монолитом -группа с неабелевым монолитом 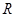 , что , что 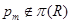 , , 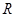 совпадает с совпадает с 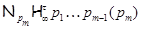 -корадикалом группы -корадикалом группы 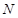 и и
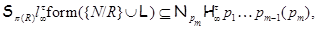
где 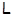 – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы 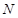 . .
Теорема 2 [10].
Пусть 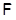 и и  – –  -замкнутые тотально насыщенные формации, -замкнутые тотально насыщенные формации,  . Тогда и только тогда . Тогда и только тогда 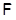 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -формация когда -формация когда 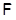 удовлетворяет одному из следующих условий: удовлетворяет одному из следующих условий:
1) 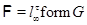 , где , где 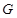 – такая монолитическая – такая монолитическая  -минимальная не -минимальная не  -группа с неабелевой минимальной нормальной подгруппой -группа с неабелевой минимальной нормальной подгруппой  , что справедливо включение , что справедливо включение
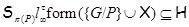 , где , где 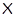 – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы 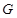 ; ;
2) 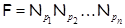 , ,
где 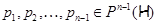 и и 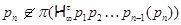 ; ;
3)  , ,
где 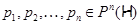 , а , а 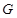 – такая монолитическая группа с неабелевой минимальной нормальной подгруппой – такая монолитическая группа с неабелевой минимальной нормальной подгруппой 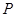 , что , что 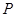 совпадает с совпадает с 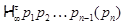 -корадикалом группы -корадикалом группы 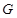 , , 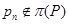 и и
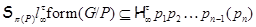 . .
В настоящей работе, основываясь на результатах работы [10], мы даем описание 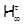 -критических формаций для некоторых наиболее известных формаций -критических формаций для некоторых наиболее известных формаций  . .
1. Определения и обозначения
Напомним, что всякую формацию групп называют 0-кратно насыщенной
. При 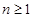 формацию формацию 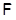 называют называют 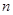 -кратно насыщенной
, если она имеет такой локальный экран, все непустые значения которого – -кратно насыщенной
, если она имеет такой локальный экран, все непустые значения которого – 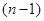 -кратно насыщенные формации. Формацию -кратно насыщенные формации. Формацию 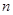 -кратно насыщенную для любого целого неотрицательного -кратно насыщенную для любого целого неотрицательного 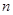 называют тотально насыщенной
. называют тотально насыщенной
.
Подгрупповым функтором
[2] называют отображение  сопоставляющее каждой группе сопоставляющее каждой группе 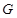 такую систему ее подгрупп такую систему ее подгрупп 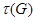 , что: 1) , что: 1)  ; 2) для любых групп ; 2) для любых групп 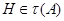 и и 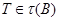 и любого эпиморфизма и любого эпиморфизма 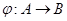 имеет место имеет место 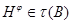 и и 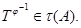
Тотально насыщенную формацию 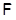 называют называют  -замкнутой
, если -замкнутой
, если 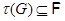 для любой группы для любой группы  . .  -Замкнутую тотально насыщенную формацию -Замкнутую тотально насыщенную формацию 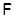 называют минимальной называют минимальной  -замкнутой тотально насыщенной не -замкнутой тотально насыщенной не  -формацией
(или, иначе, -формацией
(или, иначе, 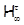 -критической
), если -критической
), если  , но все собственные , но все собственные  -замкнутые тотально насыщенные подформации из -замкнутые тотально насыщенные подформации из 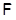 содержатся в классе групп содержатся в классе групп  . .
Пусть  – –  -замкнутая формация. Группа -замкнутая формация. Группа 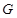 называется называется  -минимальной не -минимальной не 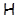 -группой
, если -группой
, если 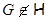 , но , но  для любой собственной подгруппы для любой собственной подгруппы 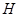 из из 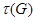 . .
Для всякой совокупности групп 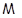 через через 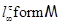 обозначают обозначают  -замкнутую тотально насыщенную формацию, порожденную классом групп -замкнутую тотально насыщенную формацию, порожденную классом групп 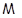 , т.е. пересечение всех
, т.е. пересечение всех  -замкнутых тотально насыщенных формаций, содержащих -замкнутых тотально насыщенных формаций, содержащих 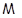 . Если . Если 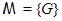 , то , то 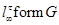 называют однопорожденной называют однопорожденной
 -замкнутой тотально насыщенной формацией. Для любых -замкнутой тотально насыщенной формацией. Для любых  -замкнутых тотально насыщенных формаций -замкнутых тотально насыщенных формаций 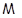 и и 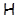 полагают полагают 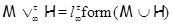 . Частично упорядоченное по включению . Частично упорядоченное по включению 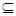 множество всех множество всех  -замкнутых тотально насыщенных формаций -замкнутых тотально насыщенных формаций 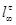 с операциями с операциями  и и 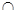 образует полную решетку. Формации из образует полную решетку. Формации из 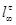 называют называют 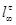 -формациями.
Экран, все непустые значения которого -формациями.
Экран, все непустые значения которого 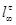 -формации, называют -формации, называют 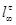 -значным
. Если -значным
. Если  – – 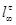 -формация, то через -формация, то через  обозначают её минимальный обозначают её минимальный 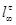 -значный локальный экран
. -значный локальный экран
.
Для произвольной последовательности простых чисел 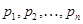 и всякой совокупности групп и всякой совокупности групп 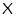 класс групп класс групп 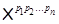 определяют следующим образом: определяют следующим образом:
1)  ; 2) ; 2) 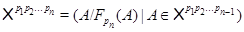 . .
Последовательность простых чисел 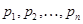 называют подходящей
для называют подходящей
для  , если , если 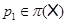 и для любого и для любого 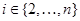 число число 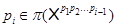 . Множество всех подходящих для . Множество всех подходящих для 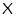 последовательностей обозначают через последовательностей обозначают через 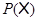 . Символом . Символом 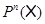 обозначают совокупность всех таких последовательностей обозначают совокупность всех таких последовательностей 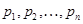 из из  , у которых , у которых 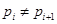 при всех при всех 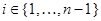 . .
Пусть 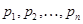 – некоторая подходящая для – некоторая подходящая для  последовательность. Тогда последовательность. Тогда 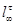 -значный локальный экран -значный локальный экран 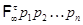 определяют следующим образом: определяют следующим образом:
1) 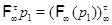 ; 2) ; 2) 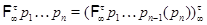 . .
В дальнейшем через 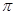 будем обозначать некоторое непустое множество простых чисел. будем обозначать некоторое непустое множество простых чисел.
2. Используемые результаты
Лемма 2.1 [9].
Пусть  – монолитическая группа, – монолитическая группа,
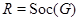 – неабелева группа. Тогда – неабелева группа. Тогда
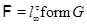 имеет единственную максимальную имеет единственную максимальную 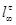 -подформацию -подформацию
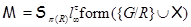 , где , где 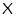 – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы 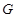 . В частности, . В частности,
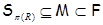 .
.
Лемма 2.2 [2,
c
. 33].
Пусть
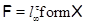 , где , где 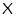 – непустой класс групп. Тогда если – непустой класс групп. Тогда если  – минимальный – минимальный 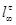 -значный экран формации -значный экран формации  , то справедливы следующие утверждения: , то справедливы следующие утверждения:
1) 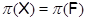 ; ;
2) 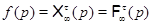
при всех простых числах  ; ;
3) если 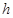 – произвольный – произвольный 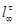 -значный экран формации -значный экран формации 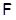 , то при любом , то при любом 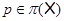 имеет место имеет место 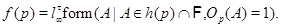
Следующая лемма является частным случаем теоремы 2.5.5 [2, c. 94].
Лемма 2.3.
Пусть  , , 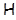 – – 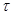 -замкнутые тотально насыщенные формации, -замкнутые тотально насыщенные формации, 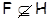 , , 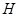 – канонический экран формации – канонический экран формации 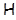 . Тогда . Тогда  является является 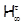 -критической формацией в том и только в том случае, когда -критической формацией в том и только в том случае, когда
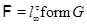 , где , где 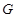 – такая монолитическая – такая монолитическая 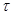 -минимальная не -минимальная не 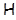 -группа с монолитом -группа с монолитом  , что для всех , что для всех 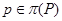 формация формация   -критична. -критична.
3. Основные результаты
Теоремы 1 и 2 могут быть использованы для нахождения описания минимальных 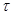 -замкнутых тотально насыщенных не -замкнутых тотально насыщенных не 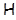 -формаций для большинства «классических», наиболее часто используемых в приложениях классов групп -формаций для большинства «классических», наиболее часто используемых в приложениях классов групп  , поскольку большинство из них являются наследственными тотально насыщенными формациями. Приведем описание , поскольку большинство из них являются наследственными тотально насыщенными формациями. Приведем описание  -критических формаций для некоторых конкретных классов групп -критических формаций для некоторых конкретных классов групп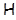 . .
Минимальные  -замкнутые тотально насыщенные не -замкнутые тотально насыщенные не 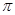 -разрешимые формации. -разрешимые формации.
Напомним, что группу  называют называют 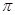 -разрешимой, если -разрешимой, если  для каждого ее главного для каждого ее главного 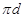 -фактора -фактора 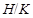 . Пусть . Пусть 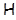 – формация всех – формация всех 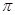 -разрешимых групп. Тогда, очевидно, -разрешимых групп. Тогда, очевидно,  . Класс всех . Класс всех 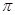 -разрешимых групп является наследственной тотально насыщенной формацией. -разрешимых групп является наследственной тотально насыщенной формацией.
Теорема 3.1.
Тогда и только тогда  – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 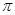 -разрешимая формация, когда -разрешимая формация, когда
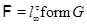 , где , где 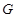 – монолитическая – монолитическая 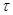 -минимальная не -минимальная не 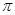 -разрешимая группа с таким неабелевым монолитом -разрешимая группа с таким неабелевым монолитом 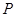 , что , что 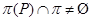 и группа и группа 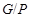 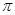 -разрешима
. -разрешима
.
Доказательство.
Необходимость.
Пусть  – минимальная – минимальная 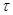 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 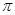 -разрешимая формация. По теореме 1 имеем -разрешимая формация. По теореме 1 имеем 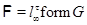 , где , где  – такая монолитическая – такая монолитическая 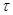 -минимальная не -минимальная не 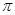 -разрешимая группа с монолитом -разрешимая группа с монолитом 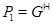 , что выполняется одно из следующих условий: , что выполняется одно из следующих условий:
1) 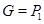 – группа простого порядка – группа простого порядка 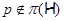 ; ;
2) 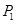 – неабелева группа и – неабелева группа и 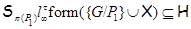 , где , где  – совокупность всех собственных – совокупность всех собственных 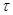 -подгрупп группы -подгрупп группы  ; ;
3) 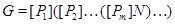 , ,
где 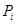 – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в 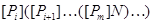 при всех при всех 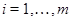 , а , а 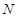 либо группа простого порядка либо группа простого порядка 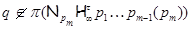 , либо такая монолитическая , либо такая монолитическая 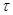 -минимальная не -минимальная не 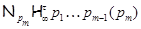 -группа с неабелевым монолитом -группа с неабелевым монолитом 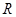 , что , что 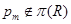 , , 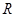 совпадает с совпадает с 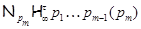 -корадикалом группы -корадикалом группы 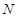 и и

где  – совокупность всех собственных – совокупность всех собственных 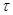 -подгрупп группы -подгрупп группы 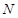 . .
Поскольку  , то , то  – неабелева группа и – неабелева группа и  . Таким образом, группа . Таким образом, группа 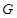 удовлетворяет условию теоремы. удовлетворяет условию теоремы.
Достаточность.
Пусть 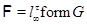 , где , где 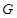 – группа из условия теоремы. Ввиду леммы 2.1 формация – группа из условия теоремы. Ввиду леммы 2.1 формация 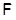 имеет единственную максимальную имеет единственную максимальную 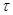 -замкнутая тотально насыщенную подформацию -замкнутая тотально насыщенную подформацию 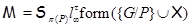 , где , где  – совокупность всех собственных – совокупность всех собственных 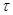 -подгрупп группы -подгрупп группы 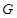 . Поскольку . Поскольку 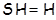 и и 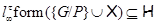 , то , то 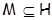 . Следовательно, . Следовательно, 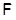 – минимальная – минимальная 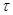 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 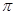 -разрешимая формация. Теорема доказана. -разрешимая формация. Теорема доказана.
Следствие 3.1.1.
Тогда и только тогда 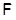 – минимальная – минимальная 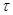 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -разрешимая формация, когда -разрешимая формация, когда
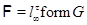 , где , где 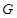 – монолитическая – монолитическая 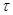 -минимальная не -минимальная не  -разрешимая группа с таким неабелевым монолитом -разрешимая группа с таким неабелевым монолитом  , что , что 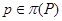 и группа и группа 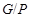  -разрешима. -разрешима.
Следствие 3.1.2 [9].
Тогда и только тогда 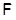 – минимальная – минимальная 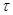 -замкнутая тотально насыщенная неразрешимая формация, когда -замкнутая тотально насыщенная неразрешимая формация, когда
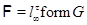 , где , где 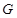 – монолитическая – монолитическая 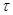 -минимальная неразрешимая группа с таким неабелевым монолитом -минимальная неразрешимая группа с таким неабелевым монолитом  , что группа , что группа 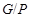 разрешима. разрешима.
Если 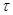 – тривиальный подгрупповой функтор, т.е.
– тривиальный подгрупповой функтор, т.е. 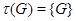 из теоремы 3.1 вытекает из теоремы 3.1 вытекает
Следствие 3.1.3.
Тогда и только тогда 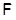 – минимальная тотально насыщенная не – минимальная тотально насыщенная не 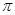 -разрешимая формация, когда -разрешимая формация, когда
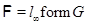 , где , где  – монолитическая группа с таким неабелевым монолитом – монолитическая группа с таким неабелевым монолитом  , что , что  и группа и группа 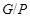 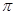 -разрешима
. -разрешима
.
Следствие 3.1.4 [7].
Тогда и только тогда 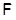 – минимальная тотально насыщенная неразрешимая формация, когда – минимальная тотально насыщенная неразрешимая формация, когда
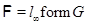 , где , где 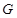 – монолитическая группа с таким неабелевым монолитом – монолитическая группа с таким неабелевым монолитом  , что группа , что группа 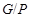 разрешима
. разрешима
.
В случае, когда 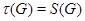 – совокупность всех подгрупп группы – совокупность всех подгрупп группы 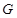 из теоремы 3.1 получаем из теоремы 3.1 получаем
Следствие 3.1.5.
Тогда и только тогда 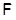 – минимальная наследственная тотально насыщенная не – минимальная наследственная тотально насыщенная не 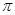 -разрешимая формация, когда -разрешимая формация, когда
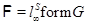 , где , где 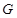 – простая неабелева минимальная не – простая неабелева минимальная не 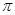 -разрешимая группа. -разрешимая группа.
Следствие 3.1.6.
Тогда и только тогда 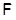 – минимальная наследственная тотально насыщенная не – минимальная наследственная тотально насыщенная не  -разрешимая формация, когда -разрешимая формация, когда
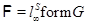 , где , где 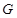 – простая неабелева минимальная не – простая неабелева минимальная не 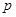 -разрешимая группа. -разрешимая группа.
Следствие 3.1.7.
Тогда и только тогда 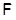 – минимальная наследственная тотально насыщенная неразрешимая формация, когда – минимальная наследственная тотально насыщенная неразрешимая формация, когда
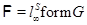 , где , где 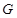 – простая неабелева минимальная неразрешимая группа. – простая неабелева минимальная неразрешимая группа.
Если 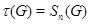 – совокупность всех нормальных подгрупп группы – совокупность всех нормальных подгрупп группы 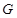 имеем имеем
Следствие 3.1.8.
Тогда и только тогда 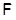 – минимальная нормально наследственная тотально насыщенная не – минимальная нормально наследственная тотально насыщенная не 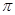 -разрешимая формация, когда -разрешимая формация, когда
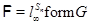 , где , где  – простая неабелева – простая неабелева 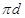 -группа. -группа.
Следствие 3.1.9.
Тогда и только тогда  – минимальная нормально наследственная тотально насыщенная не – минимальная нормально наследственная тотально насыщенная не  -разрешимая формация, когда -разрешимая формация, когда
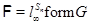 , где , где  – простая неабелева – простая неабелева 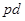 -группа. -группа.
Следствие 3.1.10.
Тогда и только тогда  – минимальная нормально наследственная тотально насыщенная неразрешимая формация, когда – минимальная нормально наследственная тотально насыщенная неразрешимая формация, когда
 , где , где  – простая неабелева группа. – простая неабелева группа.
Минимальные 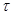 -замкнутые тотально насыщенные не -замкнутые тотально насыщенные не 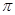 -нильпотентные формации. -нильпотентные формации.
Группа  называется называется  -нильпотентной, если она имеет нормальную -нильпотентной, если она имеет нормальную 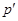 -холловскую подгруппу для каждого -холловскую подгруппу для каждого 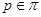 . Класс всех . Класс всех 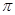 -нильпотентных групп совпадает с произведением -нильпотентных групп совпадает с произведением 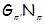 и является наследственной тотально насыщенной формацией. и является наследственной тотально насыщенной формацией.
Теорема 3.2.
Тогда и только тогда  – минимальная – минимальная 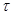 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -нильпотентная формация, когда -нильпотентная формация, когда
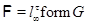 , где , где  – не – не 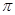 -нильпотентная группа Шмидта. -нильпотентная группа Шмидта.
Доказательство.
Пусть 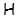 формацию всех формацию всех  -нильпотентных групп. -нильпотентных групп.
Необходимость.
Пусть  – минимальная – минимальная 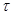 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -нильпотентная формация. В силу теоремы 1 имеет место -нильпотентная формация. В силу теоремы 1 имеет место 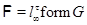 , где , где  – такая монолитическая – такая монолитическая 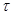 -минимальная не -минимальная не  -нильпотентная группа с монолитом -нильпотентная группа с монолитом 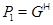 , что выполняется одно из следующих условий: , что выполняется одно из следующих условий:
1) 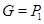 – группа простого порядка – группа простого порядка 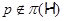 ; ;
2) 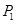 – неабелева группа и – неабелева группа и 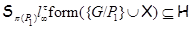 , где , где 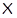 – совокупность всех собственных – совокупность всех собственных 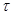 -подгрупп группы -подгрупп группы  ; ;
3) 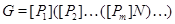 , ,
где  – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в  при всех при всех 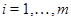 , а , а 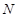 либо группа простого порядка либо группа простого порядка 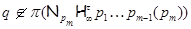 , либо такая монолитическая , либо такая монолитическая 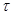 -минимальная не -минимальная не 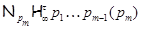 -группа с неабелевым монолитом -группа с неабелевым монолитом 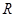 , что , что 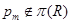 , , 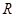 совпадает с совпадает с 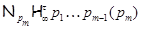 -корадикалом группы -корадикалом группы 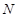 и и
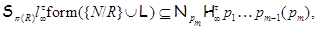
где 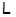 – совокупность всех собственных – совокупность всех собственных 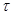 -подгрупп группы -подгрупп группы  . .
Поскольку 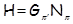 , то первые два случая невозможны. Поэтому , то первые два случая невозможны. Поэтому 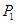 – абелева – абелева 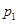 -группа, где -группа, где 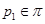 . По лемме 2.2 имеем . По лемме 2.2 имеем 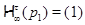 . Поэтому . Поэтому 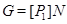 , где , где  – группа простого порядка. Таким образом, – группа простого порядка. Таким образом,  – не – не  -нильпотентная группа Шмидта. -нильпотентная группа Шмидта.
Достаточность.
Пусть 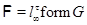 , где , где  – не – не 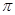 -нильпотентная группа Шмидта. Поскольку -нильпотентная группа Шмидта. Поскольку  насыщенная формация, то без ограничения общности можно считать, что насыщенная формация, то без ограничения общности можно считать, что 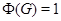 . Поэтому . Поэтому 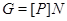 , где , где  – минимальная нормальная – минимальная нормальная  -подгруппа группы -подгруппа группы  , , 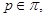 а а 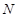 – группа простого порядка – группа простого порядка 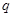 . Так как группа . Так как группа  и все собственные подгруппы из и все собственные подгруппы из  нильпотентны, а следовательно, и нильпотентны, а следовательно, и 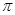 -нильпотентны, то -нильпотентны, то  – – 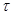 -минимальная не -минимальная не  -нильпотентная группа и -нильпотентная группа и 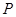 – –  -нильпотентный корадикал группы -нильпотентный корадикал группы  . Используя теперь теорему 1 заключаем, что . Используя теперь теорему 1 заключаем, что  – минимальная – минимальная 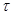 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -нильпотентная формация. Теорема доказана. -нильпотентная формация. Теорема доказана.
Используя теорему 2, получим
Следствие 3.2.1.
Тогда и только тогда  – минимальная – минимальная 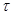 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -нильпотентная формация, когда -нильпотентная формация, когда
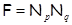 , где , где  и и 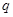 – различные простые числа, – различные простые числа, 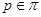 . .
В случае, когда 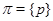 из теорем 3.2 и 2 вытекают из теорем 3.2 и 2 вытекают
Следствие 3.2.2.
Тогда и только тогда  – минимальная – минимальная 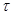 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -нильпотентная формация, когда -нильпотентная формация, когда
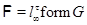 , где , где  – не – не  -нильпотентная группа Шмидта. -нильпотентная группа Шмидта.
Следствие 3.2.3.
Тогда и только тогда  – минимальная – минимальная 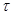 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -нильпотентная формация, когда -нильпотентная формация, когда
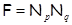 , где , где 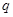 – отличное – отличное
 простое число. простое число.
Если теперь  – множество всех простых чисел из теоремы 3.2 получаем – множество всех простых чисел из теоремы 3.2 получаем
Следствие 3.2.4.
Тогда и только тогда  – минимальная – минимальная 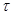 -замкнутая тотально насыщенная ненильпотентная формация, когда -замкнутая тотально насыщенная ненильпотентная формация, когда
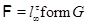 , где , где  – некоторая группа Шмидта. – некоторая группа Шмидта.
Следствие 3.2.5.
Тогда и только тогда  – минимальная – минимальная 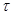 -замкнутая тотально насыщенная ненильпотентная формация, когда -замкнутая тотально насыщенная ненильпотентная формация, когда
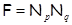 , где , где  и и 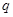 – различные простые числа. – различные простые числа.
Следствие 3.2.6 [7].
Тогда и только тогда  – минимальная тотально насыщенная ненильпотентная формация, когда – минимальная тотально насыщенная ненильпотентная формация, когда
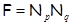 , где , где  и и 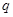 – различные простые числа. – различные простые числа.
Минимальные 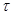 -замкнутые тотально насыщенные не -замкнутые тотально насыщенные не 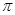 -замкнутые формации. -замкнутые формации.
Напомним, что группа называется  -замкнутой, если она имеет нормальную -замкнутой, если она имеет нормальную 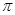 -холловскую подгруппу. Формация всех -холловскую подгруппу. Формация всех  -замкнутых групп, очевидно, совпадает с произведением -замкнутых групп, очевидно, совпадает с произведением 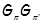 и является наследственной тотально насыщенной формацией. и является наследственной тотально насыщенной формацией.
Теорема 3.3.
Тогда и только тогда  – минимальная – минимальная 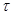 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -замкнутая формация, когда -замкнутая формация, когда
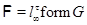 , где , где  – не – не 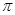 -замкнутая группа Шмидта. -замкнутая группа Шмидта.
Доказательство.
Обозначим через 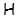 формацию всех формацию всех 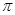 -замкнутых групп. -замкнутых групп.
Необходимость.
Пусть  – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -замкнутая формация. По теореме 1 имеем -замкнутая формация. По теореме 1 имеем 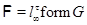 , где , где  – такая монолитическая – такая монолитическая  -минимальная не -минимальная не  -замкнутая группа с монолитом -замкнутая группа с монолитом 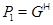 , что выполняется одно из следующих условий: , что выполняется одно из следующих условий:
1) 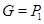 – группа простого порядка – группа простого порядка 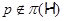 ; ;
2) 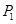 – неабелева группа и – неабелева группа и 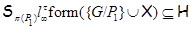 , где , где 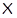 – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы  ; ;
3) 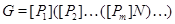 , ,
где 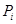 – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в  при всех при всех 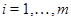 , а , а 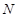 либо группа простого порядка либо группа простого порядка 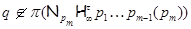 , либо такая монолитическая , либо такая монолитическая  -минимальная не -минимальная не 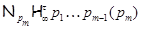 -группа с неабелевым монолитом -группа с неабелевым монолитом 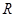 , что , что 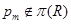 , , 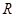 совпадает с совпадает с 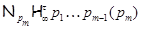 -корадикалом группы -корадикалом группы 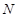 и и
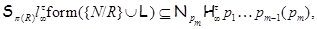
где 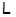 – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы  . .
Так как 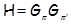 , то , то 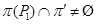 . Если . Если 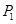 – неабелева группа, то по лемме 2.2 имеем – неабелева группа, то по лемме 2.2 имеем 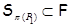 . Значит, . Значит, 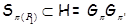 Противоречие. Поэтому Противоречие. Поэтому 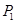 – абелева – абелева 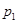 -группа, где -группа, где 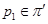 . Значит, . Значит, 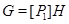 для некоторой максимальной подгруппы для некоторой максимальной подгруппы 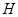 группы группы  . В силу леммы 2.3 получаем, что . В силу леммы 2.3 получаем, что 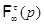 – – 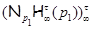 -критическая формация. Согласно лемме 2.2 имеем -критическая формация. Согласно лемме 2.2 имеем  . Так как . Так как  , то , то 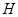 – группа простого порядка – группа простого порядка 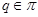 . Таким образом, . Таким образом,  – не – не 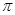 -замкнутая группа Шмидта. -замкнутая группа Шмидта.
Достаточность.
Пусть 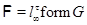 , где , где  – не – не  -замкнутая группа Шмидта. Так как -замкнутая группа Шмидта. Так как  – насыщенная формация, то не ограничивая общности можно считать, что – насыщенная формация, то не ограничивая общности можно считать, что 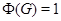 . Поэтому . Поэтому 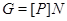 , где , где 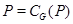 – минимальная нормальная – минимальная нормальная  -подгруппа -подгруппа  , ,  , , 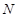 – группа простого порядка – группа простого порядка 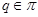 . Так как группа . Так как группа  и любая собственная подгруппа из и любая собственная подгруппа из  нильпотентны, а значит, и нильпотентны, а значит, и  -замкнуты, то -замкнуты, то  – – 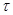 -минимальная не -минимальная не 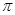 -замкнутая группа и -замкнутая группа и 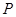 её её  -замкнутый корадикал. Теперь, в силу теоремы 1, мы можем заключить, что -замкнутый корадикал. Теперь, в силу теоремы 1, мы можем заключить, что  – минимальная – минимальная 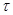 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 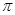 -замкнутая формация. Теорема доказана. -замкнутая формация. Теорема доказана.
Следствие 3.3.1.
Тогда и только тогда  – минимальная – минимальная 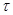 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -замкнутая формация, когда -замкнутая формация, когда
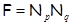 , где , где 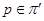 и и 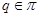 .
.
В случае, когда 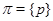 из теоремы 3.3 вытекает из теоремы 3.3 вытекает
Следствие 3.3.2.
Тогда и только тогда  – минимальная – минимальная 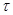 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -замкнутая формация, когда -замкнутая формация, когда
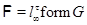 , где , где  – не – не  -замкнутая группа Шмидта. -замкнутая группа Шмидта.
Следствие 3.3.3.
Тогда и только тогда  – минимальная – минимальная 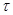 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -замкнутая формация, когда -замкнутая формация, когда
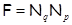 , где , где 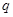 – отличное от – отличное от  простое число. простое число.
Минимальные  -замкнутые тотально насыщенные не -замкнутые тотально насыщенные не 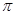 -специальные формации. -специальные формации.
Группа называется 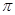 -специальной, если она обладает нильпотентной нормальной -специальной, если она обладает нильпотентной нормальной 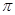 -холловской подгруппой. Понятно, что совокупность всех -холловской подгруппой. Понятно, что совокупность всех 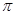 -специальных групп совпадает с классом -специальных групп совпадает с классом 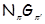 и является наследственной тотально насыщенной формацией. и является наследственной тотально насыщенной формацией.
Теорема 3.4.
Тогда и только тогда  – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 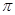 -специальная формация, когда -специальная формация, когда
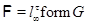 , где , где  – не – не 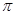 -специальная группа Шмидта. -специальная группа Шмидта.
Доказательство.
Пусть 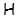 обозначает формацию всех обозначает формацию всех 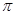 -специальных групп. -специальных групп.
Необходимость.
Если  – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 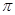 -специальная формация, то по теореме 1 имеет место -специальная формация, то по теореме 1 имеет место 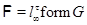 , где , где  – такая монолитическая – такая монолитическая  -минимальная не -минимальная не 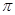 -специальная группа с монолитом -специальная группа с монолитом 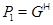 , что выполняется одно из следующих условий: , что выполняется одно из следующих условий:
1) 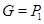 – группа простого порядка – группа простого порядка 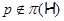 ; ;
2) 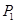 – неабелева группа и – неабелева группа и  , где , где 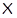 – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы  ; ;
3) 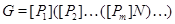 , ,
где 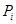 – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в 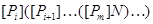 при всех при всех 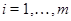 , а , а 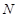 либо группа простого порядка либо группа простого порядка 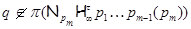 , либо такая монолитическая , либо такая монолитическая  -минимальная не -минимальная не 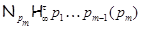 -группа с неабелевым монолитом -группа с неабелевым монолитом 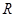 , что , что 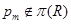 , , 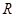 совпадает с совпадает с 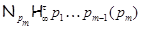 -корадикалом группы -корадикалом группы 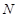 и и
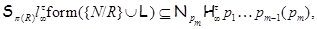
где 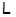 – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы 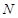 . .
Поскольку 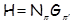 , то случай 1) не имеет место и , то случай 1) не имеет место и 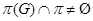 . Если . Если 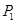 – неабелева группа, то в силу леммы 2.1 имеем – неабелева группа, то в силу леммы 2.1 имеем  . Поэтому . Поэтому  и и 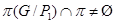 . Пусть . Пусть  и и 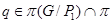 . Тогда в силу леммы 2.1 имеет место включение . Тогда в силу леммы 2.1 имеет место включение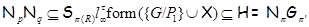 . Противоречие. Поэтому невозможен и случай 2). Следовательно, . Противоречие. Поэтому невозможен и случай 2). Следовательно, 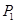 – абелева – абелева 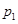 -группа. Так как имеют место равенства -группа. Так как имеют место равенства 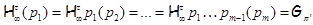 , то , то 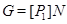 , где , где 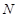 – группа порядка – группа порядка  . Таким образом, . Таким образом, 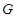 – не – не 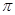 -специальная группа Шмидта. -специальная группа Шмидта.
Достаточность.
Пусть 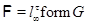 , где , где 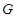 – не – не 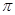 -специальная группа Шмидта. Тогда -специальная группа Шмидта. Тогда 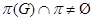 . Поскольку . Поскольку  – насыщенная формация, то без ограничения общности можно считать, что – насыщенная формация, то без ограничения общности можно считать, что 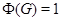 . Поэтому . Поэтому 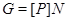 , где , где 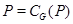 – минимальная нормальная – минимальная нормальная  -подгруппа -подгруппа 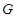 , а , а 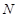 – группа простого порядка – группа простого порядка 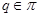 . Ввиду того, что группа . Ввиду того, что группа 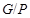 и любая собственная подгруппа из и любая собственная подгруппа из 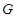 нильпотентны, а следовательно, и нильпотентны, а следовательно, и 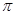 -специальны, то -специальны, то 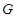 – –  -минимальная не -минимальная не 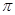 -специальная группа и -специальная группа и 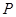 её её 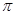 -специальный корадикал. Привлекая теперь теорему 1 заключаем, что -специальный корадикал. Привлекая теперь теорему 1 заключаем, что 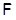 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 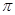 -специальная формация. Теорема доказана. -специальная формация. Теорема доказана.
Следствие 3.4.1.
Тогда и только тогда  – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 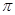 -специальная формация, когда -специальная формация, когда
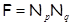 , где , где  и и 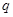 – различные простые числа, – различные простые числа,  . .
В случае, когда 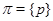 из теоремы 3.4 вытекает из теоремы 3.4 вытекает
Следствие 3.4.2.
Тогда и только тогда 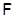 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -специальная формация, когда -специальная формация, когда
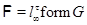 , где , где 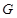 – не – не  -специальная группа Шмидта. -специальная группа Шмидта.
Следствие 3.4.3.
Тогда и только тогда 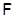 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -специальная формация, когда -специальная формация, когда
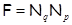 , где , где 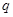 – отличное от – отличное от  простое число. простое число.
Минимальные  -замкнутые тотально насыщенные не -замкнутые тотально насыщенные не 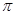 -разложимые формации. -разложимые формации.
Группа называется 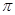 -разложимой, если она одновременно -разложимой, если она одновременно 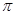 -специальна и -специальна и  -замкнута. -замкнута.
Класс всех 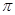 -разложимых групп совпадает с пересечением -разложимых групп совпадает с пересечением  и является наследственной тотально насыщенной формацией. и является наследственной тотально насыщенной формацией.
Теорема 3.5.
Тогда и только тогда 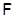 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 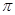 -разложимая формация, когда -разложимая формация, когда
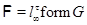 , где , где 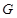 – не – не 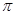 -разложимая группа Шмидта. -разложимая группа Шмидта.
Доказательство.
Обозначим через 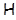 формацию всех формацию всех 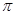 -разложимых групп. -разложимых групп.
Необходимость.
Пусть 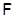 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 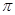 - разложимая формация. В силу теорем 3.3 и 3.4 имеем - разложимая формация. В силу теорем 3.3 и 3.4 имеем 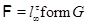 , где , где 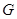 – такая группа Шмидта, что – такая группа Шмидта, что  . Таким образом, . Таким образом, 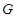 – не – не 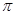 - разложимая группа Шмидта. - разложимая группа Шмидта.
Достаточность.
Пусть 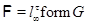 , где , где 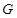 – не – не 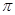 -разложимая группа Шмидта. Поэтому -разложимая группа Шмидта. Поэтому 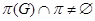 . Ввиду насыщенности формации . Ввиду насыщенности формации 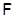 можно считать, что можно считать, что  . Значит, . Значит, 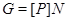 , где , где 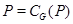 – минимальная нормальная – минимальная нормальная  -подгруппа -подгруппа  , а , а 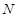 – группа простого порядка. Поскольку группа – группа простого порядка. Поскольку группа  и любая собственная подгруппа из и любая собственная подгруппа из 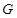 нильпотентны, а значит, и нильпотентны, а значит, и 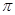 -разложимы, то -разложимы, то 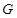 – –  -минимальная не -минимальная не 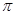 -разложимая группа и -разложимая группа и 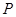 её её 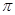 -разложимый корадикал. В силу теоремы 1 имеем -разложимый корадикал. В силу теоремы 1 имеем 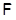 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 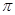 -разложимая формация. Теорема доказана. -разложимая формация. Теорема доказана.
Следствие 3.5.1.
Тогда и только тогда 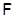 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 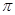 -разложимая формация, когда -разложимая формация, когда
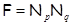 , где , где
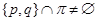 . .
В случае, когда 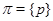 из теоремы 3.24 вытекает из теоремы 3.24 вытекает
Следствие 3.5.2.
Тогда и только тогда 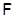 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -разложимая формация, когда -разложимая формация, когда
 , где , где  – не – не  -разложимая группа Шмидта. -разложимая группа Шмидта.
Следствие 3.5.3.
Тогда и только тогда 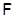 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не  -разложимая формация, когда -разложимая формация, когда
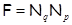 , где , где 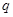 – отличное от – отличное от  простое число. простое число.
Минимальные  -замкнутые тотально насыщенные не -замкнутые тотально насыщенные не 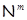 -формации. -формации.
Класс всех разрешимых групп с нильпотентной длиной не превосходящей 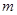 совпадает с произведением совпадает с произведением 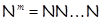 (число сомножителей равно (число сомножителей равно 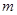 ) и является наследственной тотально насыщенной формацией. ) и является наследственной тотально насыщенной формацией.
Теорема 3.6.
Тогда и только тогда 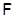 – минимальная тотально насыщенная не – минимальная тотально насыщенная не 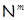 -формация, когда -формация, когда
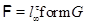 , где , где 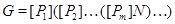 – минимальная не – минимальная не 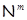 -группа, -группа, 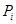 – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в 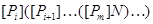 при всех при всех  и и  – группа простого порядка. – группа простого порядка.
Доказательство.
Обозначим через 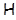 формацию формацию 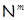 .
.
Необходимость.
Пусть 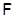 – минимальная – минимальная  -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 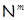 -формация. По теореме 1
-формация. По теореме 1 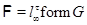 , где , где  – такая монолитическая – такая монолитическая  -минимальная не -минимальная не 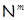 -
группа с монолитом -
группа с монолитом 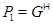 , что выполняется одно из следующих условий: , что выполняется одно из следующих условий:
1) 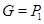 – группа простого порядка – группа простого порядка 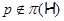 ; ;
2) 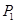 – неабелева группа и – неабелева группа и 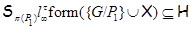 , где , где  – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы 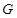 ; ;
3) 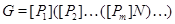 , ,
где 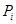 – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в 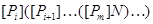 при всех при всех 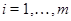 , а , а  либо группа простого порядка либо группа простого порядка  , либо такая монолитическая , либо такая монолитическая  -минимальная не -минимальная не 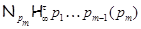 -группа с неабелевым монолитом -группа с неабелевым монолитом  , что , что 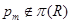 , , 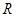 совпадает с совпадает с 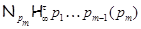 -корадикалом группы -корадикалом группы  и и
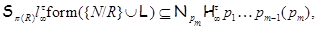
где  – совокупность всех собственных – совокупность всех собственных  -подгрупп группы -подгрупп группы 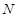 . .
Поскольку  , то случай 1) невозможен. Если группа
, то случай 1) невозможен. Если группа 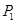 неабелева, то по лемме 2.1 неабелева, то по лемме 2.1 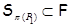 , что невозможно. Следовательно, имеет место случай 3). Поскольку группа , что невозможно. Следовательно, имеет место случай 3). Поскольку группа 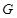 разрешима, то разрешима, то 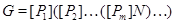 , где , где 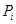 – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в  при всех при всех 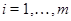 , а , а 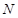 группа простого порядка группа простого порядка 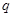 . Таким образом, группа . Таким образом, группа удовлетворяет условию теоремы. удовлетворяет условию теоремы.
Достаточность
вытекает из теоремы 1. Теорема доказана.
Следствие 3.6.1 [2, с. 94].
Пусть 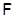 – разрешимая формация.
Тогда и только тогда – разрешимая формация.
Тогда и только тогда 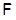 – минимальная тотально насыщенная не – минимальная тотально насыщенная не 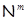 -формация, когда -формация, когда
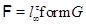 , где , где 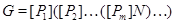 – минимальная не – минимальная не 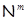 -группа, -группа, 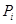 – самоцентрализуемая минимальная нормальная подгруппа в – самоцентрализуемая минимальная нормальная подгруппа в 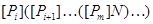 при всех при всех  и и 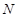 – группа простого порядка. – группа простого порядка.
Следствие 3.6.2.
Тогда и только тогда 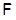 – минимальная тотально насыщенная не – минимальная тотально насыщенная не 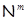 -формация, когда -формация, когда 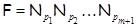 для некоторой последовательности для некоторой последовательности 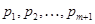 из из 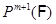 . .
Следствие 3.6.3 [2, с. 94].
Пусть 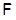 – разрешимая формация.
Тогда и только тогда – разрешимая формация.
Тогда и только тогда 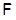 – минимальная тотально насыщенная не – минимальная тотально насыщенная не  -формация, когда -формация, когда 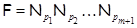 для некоторой последовательности для некоторой последовательности 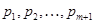 из из  . .
Отметим, что полученные результаты могут быть использованы для описания 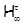 -критических формаций и в случаях, когда формация -критических формаций и в случаях, когда формация 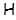 не является тотально насыщенной. не является тотально насыщенной.
Минимальные 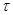 -замкнутые тотально насыщенные не -замкнутые тотально насыщенные не 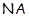 -формации. -формации.
Класс всех групп с нильпотентным коммутантом, очевидно, совпадает с произведением 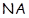 , где , где 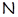 – класс всех нильпотентных, а – класс всех нильпотентных, а 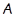 – класс всех абелевых групп. Формация – класс всех абелевых групп. Формация 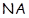 не является тотально насыщенной, но содержит единственную максимальную наследственную тотально насыщенную подформацию не является тотально насыщенной, но содержит единственную максимальную наследственную тотально насыщенную подформацию 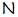 . Следовательно, любая минимальная . Следовательно, любая минимальная 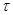 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 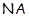 -формация является минимальной -формация является минимальной 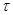 -замкнутой тотально насыщенной не -замкнутой тотально насыщенной не 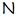 -формацией. Таким образом, привлекая следствия 3.2.4 и 3.2.5, получим -формацией. Таким образом, привлекая следствия 3.2.4 и 3.2.5, получим
Теорема 3.7.
Тогда и только тогда 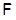 – минимальная – минимальная 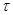 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 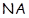 -формация, когда -формация, когда
 , где , где 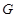 – некоторая группа Шмидта. – некоторая группа Шмидта.
Следствие 3.7.1.
Тогда и только тогда 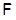 – минимальная – минимальная 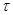 -замкнутая тотально насыщенная не -замкнутая тотально насыщенная не 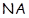 -формация, когда -формация, когда
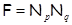 , где , где 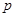 и и 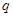 – различные простые числа. – различные простые числа.
Минимальные 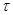 -замкнутые тотально насыщенные несверхразрешимые формации. -замкнутые тотально насыщенные несверхразрешимые формации.
Пусть 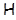 формация всех сверхразрешимых групп. Как известно (см., например, [2, с. 28]), формация формация всех сверхразрешимых групп. Как известно (см., например, [2, с. 28]), формация 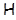 не является тотально насыщенной. Однако не является тотально насыщенной. Однако 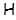 содержит единственную максимальную наследственную тотально насыщенную подформацию содержит единственную максимальную наследственную тотально насыщенную подформацию 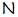 . Поэтому любая минимальная . Поэтому любая минимальная 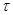 -замкнутая тотально насыщенная несверхразрешимая формация является минимальной -замкнутая тотально насыщенная несверхразрешимая формация является минимальной 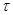 -замкнутой тотально насыщенной ненильпотентной формацией. Значит, в силу следствий 3.2.4 и 3.2.5, имеют место -замкнутой тотально насыщенной ненильпотентной формацией. Значит, в силу следствий 3.2.4 и 3.2.5, имеют место
Теорема 3.8.
Тогда и только тогда 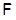 – минимальная – минимальная 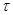 -замкнутая тотально насыщенная несверхразрешимая формация, когда -замкнутая тотально насыщенная несверхразрешимая формация, когда
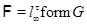 , где , где 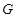 – некоторая группа Шмидта. – некоторая группа Шмидта.
Следствие 3.8.1.
Тогда и только тогда 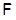 – минимальная – минимальная 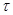 -замкнутая тотально насыщенная несверхразрешимая формация, когда -замкнутая тотально насыщенная несверхразрешимая формация, когда
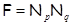 , где , где 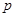 и и 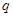 – различные простые числа. – различные простые числа.
Заключение
В работе изучаются минимальные 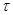 -замкнутые тотально насыщенные не -замкнутые тотально насыщенные не 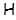 -формации конечных групп. При этом -формации конечных групп. При этом 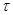 -замкнутую тотально насыщенную формацию -замкнутую тотально насыщенную формацию 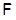 называют минимальной называют минимальной 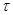 -замкнутой тотально насыщенной не -замкнутой тотально насыщенной не 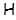 -формацией или -формацией или  -критической, если -критической, если 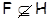 , но все собственные , но все собственные 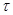 -замкнутые тотально насыщенные подформации из -замкнутые тотально насыщенные подформации из 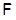 содержатся в классе групп содержатся в классе групп 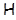 . Получено описание . Получено описание 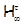 -критических формаций для таких классов групп -критических формаций для таких классов групп 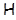 , как классы всех , как классы всех 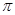 -разрешимых, -разрешимых, 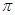 -нильпотентных, -нильпотентных,  -замкнутых, -замкнутых, 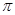 -специальных, -специальных, 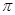 -разложимых групп ( -разложимых групп (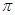 – некоторое непустое подмножество множества всех простых чисел), класс разрешимых групп нильпотентной длины не превосходящей – некоторое непустое подмножество множества всех простых чисел), класс разрешимых групп нильпотентной длины не превосходящей 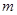 ( ( – некоторое натуральное число), класс всех групп с нильпотентным коммутантом, класс всех сверхразрешимых групп. – некоторое натуральное число), класс всех групп с нильпотентным коммутантом, класс всех сверхразрешимых групп.
Литература
1. Шеметков, Л.А. Формации алгебраических систем / Л. А. Шеметков, А. Н. Скиба // М.: Наука, 1989.
2. Скиба, А.Н. Алгебра формаций / А. Н. Скиба // Мн.: Беларуская навука, 1997.
3. Шеметков, Л.А. Экраны ступенчатых формаций / Л. А. Шеметков // Тр. VI Всесоюзн. симпозиум по теории групп. – Киев: Наукова думка, 1980. – С. 37-50.
4. Скиба, А.Н. О критических формациях / А. Н. Скиба // Изв. АН БССР. Сер. физ.-мат. наук. 1980. – № 4. – С. 27-33.
5. Скиба, А.Н. О критических формациях / А. Н. Скиба // В кн.: Бесконечные группы и примыкающие алгебраические структуры. Киев: Ин-т математики АН Украины, 1993. – С. 258-268.
6. Сафонов, В.Г. О тотально насыщенных формациях конечной длины / В. Г. Сафонов // Известия Гомельского госуниверситета, 2004. – № 6. – С. 150-155.
7. Сафонов, В.Г. О двух задачах теории тотально насыщенных формаций / В. Г. Сафонов // Докл. НАН Беларуси, 2005. – Т. 49, № 5, – C. 16-20.
8. Сафонов, В.Г. О приводимых тотально насыщенных формациях нильпотентного дефекта 3 / В. Г. Сафонов // Известия Гомельского госуниверситета, 2005. № 4 (31). – С. 157-162.
9. Сафонов, В.Г. Характеризация разрешимых однопорожденных тотально насыщенных формаций конечных групп / В.Г. Сафонов // Сибирский матем. журнал, 2007 – Т. 48, № 1. – С. 185-191.
10. Сафонов, В.Г.  -критические формации / В. Г. Сафонов // Известия Гомельского госуниверситета, 2008. № 2 (47). – С. 169-176. -критические формации / В. Г. Сафонов // Известия Гомельского госуниверситета, 2008. № 2 (47). – С. 169-176.
|