Московский государственный институт электронной техники (Технический университет)
Реферат по математическому моделированию на тему:
«Модель высотного лифта»
Выполнил: ст. гр. МП-30 Савченко В. Ю.
Проверил: к. ф.-м. н. Лисовец Ю. П.
Москва, 2007 г.
Объект исследования
Имеется высотное здание из  этажей, в котором действуют этажей, в котором действуют  лифтов. На каждом этаже имеются две кнопки для вызова лифта. Пассажиры желающие попасть на этажи выше, нажимают кнопку «вверх», ниже – «вниз». Заранее не известно, какой лифт обслужит запрос, и на какой именно этаж выше (или ниже), относительно этажа, с которого поступил запрос, намерены попасть пассажиры. лифтов. На каждом этаже имеются две кнопки для вызова лифта. Пассажиры желающие попасть на этажи выше, нажимают кнопку «вверх», ниже – «вниз». Заранее не известно, какой лифт обслужит запрос, и на какой именно этаж выше (или ниже), относительно этажа, с которого поступил запрос, намерены попасть пассажиры.
Упрощающие предположения
лифтовый система программа
· лифты движутся с одинаковой скоростью
· высадка и посадка пассажиров производиться мгновенно
· механический износ системы не учитывается
· каждый лифт может перевозить неограниченное число пассажиров
Теоретический расчёт
Необходимо разработать модель лифтовой системы из  независимых лифтов, удовлетворяющую интересу владельцев здания в минимальности затрат на обслуживание лифтов, и пассажиров – минимальности времени ожидания. независимых лифтов, удовлетворяющую интересу владельцев здания в минимальности затрат на обслуживание лифтов, и пассажиров – минимальности времени ожидания.
Для количественной характеристики данных интересов в модель вводиться две величины. Для отдельно взятого лифта – расстояние, пройденное данным лифтом с момента начала обслуживания потребностей пассажиров. Для здания в целом – суммарное время ожидания выполнения запроса с этажа.
Оговоримся сразу, требования пассажиров и владельцев противоречат друг другу. Так если требования пассажиров имеют высший приоритет то, как только поступил запрос с этажа, система должна мгновенно отправлять лифт по направлению к запросу. В силу того, что на практике, запросов больше чем лифтов, требование о минимальности времени ожидания, будет выполняться только тогда, когда число свободных лифтов больше или равно числу запросов с этажей.
Высшая приоритетность минимальности затрат будет означать следующее, ни один лифт не сдвинется с места пока все пассажиры желающие куда-либо ехать не нажмут на кнопки вызова. И только после этого, при условии, что больше не будет запросов с этажей, лифты начнут движение.
Таким образом, необходимо найти компромиссное решение, которое будет удовлетворять интересам, как пассажиров, так и владельцев здания.
Модель системы управления
Для осуществления управления движением лифтов система хранит следующие данные:
· запросы с этажей (номер этажа и направление)
· число лифтов
· суммарное время ожидания лифтов пассажирами
На систему управления возлагаются следующие функции:
· сбор запросов пассажиров с этажей
· определение для отдельно взятого лифта ближайшего запроса, который может быть обслужен этим лифтом
· вычисление суммарного времени ожидания
Дадим некоторый комментарий по поводу функции определения ближайшего запроса. Каждый лифт может находиться в трёх состояниях это: движение вверх, движение вниз и простой. Причём если лифт выгружает или загружает пассажиров, и у него есть этажи назначения или ближайший запрос, то считается, что он к ним движется. Будем говорить, что лифт находиться в состоянии простоя тогда, когда у лифта нет ни этажей назначения, ни запросов.
Если лифт движется в некотором направлении, то для него ближайшим запросом считается любой запрос в направлении по его движению в той части здания, в которой лифт находится в данный момент. Например, лифт находится на 34-ом этаже и движется вверх к этажам назначения или запросам, неожиданно поступил запрос с 38-ого этажа на движение вверх и запрос с 37-ого на движение вниз. В данном случае, так как лифт движется вверх, система управления определит ему запрос с 38-ого этажа, как ближайший.
Если лифт стоит, то ближайшим к нему считается запрос, который находиться от него на наименьшем расстоянии в не зависимости от того, в какую сторону направлен данный запрос и из какой части издания он поступил.
Модель лифта
Лифт будет характеризоваться следующими величинами:
· номер
· текущий этаж
· текущее направление движения
· ближайший запрос
· ближайший этаж назначения
· этажи назначения
· пройденное расстояние
И выполнять следующие действия:
· принятие решения о дальнейшем направлении движения
· сбор этажей назначения
· движение к этажам назначения или запросу
· вычисление пройденного расстояния
Далее рассмотрим две модели лифта с разными правилами относительного того, куда далее следует двигаться. С целью выявления набора правил, который будет удовлетворять компромиссному решению, сформулированному выше.
Набор правил №1
· если текущий этаж, ближайший этаж назначения, начать высадку пассажиров
· если текущий этаж, ближайший запрос, начать посадку пассажиров
· если есть этажи назначения, определить ближайший
· спросить у системы управления ближайший запрос, проверить если лифты без ближайшего запроса, но находящиеся ближе к этому запросу, и если нет, то принять ближайший запрос
· если определён ближайший этаж назначения, определить направление движения к нему, решение принято
· если определён ближайший запрос, определить направление движения к нему, решение принято
· если лифт не производит загрузку или выгрузку пассажиров, то остановиться, решение принято
Данные правила указаны в порядке их приоритетности. При этом, для лифта всегда будет определяться ближайший запрос и ближайшие этаж назначения, если таковые имеются.
Набор правил №2
· если текущий этаж, ближайший этаж назначения, начать высадку пассажиров, решение принято
· если есть этажи назначения, определить ближайший, двигаться к нему, решение принято
· если текущий этаж, ближайший запрос, начать посадку пассажиров, решение принято
· спросить у системы управления ближайший запрос, проверить если лифты без ближайшего запроса, но находящиеся ближе к этому запросу, и если нет, то принять ближайший запрос
· остановиться
Правила указаны в порядке их приоритетности. Существенное отличие данного набора правил кроется в том, что по этому набору, если у лифта есть этажи назначения, то он не реагирует на новые запросы, реакция происходит только в том случае, если лифт развёз всех пассажиров.
Предполагаемые отличия
В условиях данных правил предполагаем, что модель с набором правил №1 будет обслуживать запросы пассажиров быстрее, чем №2 и при этом лифты будут проходить меньшее расстояние. Данный выигрыш будет обеспечиваться существенным отличием набора правил №2 от набора правил №1, о котором говорилось выше. И будет тем больше, чем больше число запросов по движению лифта при доставке пассажиров к этажам назначения. При наборе правил №2 запросы с этажей будут обслуживаться в порядке поступления, при наборе №1 нет.
Теперь исследуем поведение данных моделей на практике, с целью выявления оптимального набора правил.
Моделирование
Для моделирования лифтовой системы были написаны две программы на языке C++.
Будем исследовать модель 50-ти этажного здания с 4-ю лифтами. Прежде всего, приведём описание окна работающей программы:
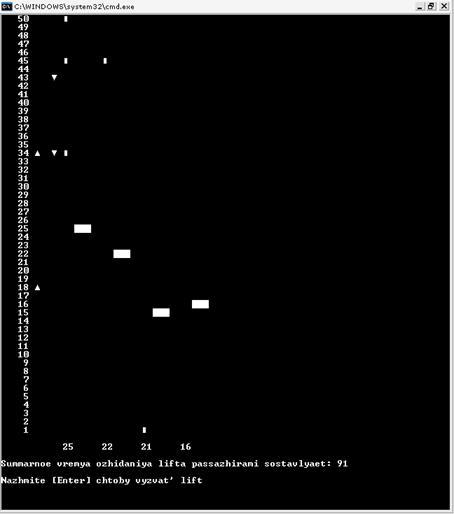
Первый столбец, состоящий из цифр – это номера этажей. Следующие два столбца отображают запросы с этажей вверх и вниз в виде треугольников. Далее большими прямоугольниками обозначаются лифты, маленькими (вдоль шахты каждого из лифтов) этажи назначения. Под шахтой каждого из лифтов находится число, характеризующее пройденное лифтом расстояние. Далее следует надпись: «Суммарное время ожидания лифтов пассажирами равно: …». И приглашение для ввода запроса. При нажатии на [Enter] система запрашивает номер этажа, на котором находиться пассажир, и направление в котором он желает двигаться. Если лифт достиг запроса, у пассажира спрашиваются этажи назначения.
Для выявления более подходящего набора правил, разработаем ряд экспериментов, и будем фиксировать реакцию системы на них. Результатом эксперимента будет суммарное расстояние, пройденное всеми лифтами, и суммарное время ожидания лифтов пассажирами.
Эксперименты
Результаты экспериментов сведём в таблицу:
| Номер эксперимента
|
Пройденные пути для №1
|
Время ожидания лифта для №1
|
Пройденные пути для №2
|
Время ожидания лифта для №2
|
| 1
|
36, 58, 78, 79
|
136
|
79, 78, 58, 36
|
140
|
| 2
|
49, 70, 84, 0
|
92
|
94, 48, 70, 0
|
115
|
| 3
|
34, 48, 49, 49
|
124
|
48, 49, 49, 38
|
128
|
| 4
|
49, 88, 0, 0
|
65
|
49, 88, 49, 68
|
105
|
| 5
|
49, 89, 0, 0
|
92
|
49, 89, 49, 49
|
99
|
Эксперимент №1
Тест направлен на моделирование ситуации, когда одновременно поступает множество запросов с верхних этажей на движение вниз, а именно:
· 50 вниз (40, 30, 20)
· 40 вниз (38, 36, 1)
· 30 вниз (20, 2, 1)
· 20 вниз (3, 5)
Как и следовало ожидать суммарные пути, пройденные лифтами равны. Время ожидания не существенно разниться. Полученные результаты объясняются тем, что не было запросов, которые можно было подхватить по движению, по этому преимущество набора правил №1 и не имеют места.
Эксперимент №2
Тест содержит один запрос, который может быть выполнен параллельно с развозом пассажиров, запросы поступили одновременно:
· 1 вверх (20, 30, 40, 50)
· 10 вверх (38, 44, 45, 49)
· 45 вниз (30, 20, 10, 5)
· 36 вниз (30, 1)
Здесь уже начинают наблюдаться преимущества модели использующей набор правил №1. Суммарный пройденный путь меньше, время ожидания так же меньше. При этом обе модели задействовали по 3 лифта для выполнения задачи.
Эксперимент №3
Одновременно поступают запросы:
· 35 вверх (45, 48, 49)
· 36 вверх (40, 50)
· 37 вверх (50 ,43 ,44)
· 20 вниз (1)
В силу одновременности, хотя и имелись запросы, расположенные по движению, существенных преимуществ модели использующей набор правил №1 не выявлено, в силу того, что лифт определяет для себя только один ближайший запрос.
Эксперимент №4
В начальный момент времени поступают запросы:
· 10 вверх (15, 27, 36, 45, 50)
· 45 вниз (1, 8, 15, 40)
Когда лифт, среагировавший на запрос с 10-ого этажа, погрузил пассажиров и получил этажи назначения, производится запрос:
· 15 вверх (34, 50)
Когда лифт, среагировавший на запрос с 45-ого этажа, погрузил пассажиров и получил этажи назначения, производится запрос:
· 35 вниз(1)
Чего и следовало ожидать, на лицо существенный выигрыш, как во времени ожидания лифтов, так и в пройденном расстоянии.
Эксперимент №5
Усугубим ситуацию, в начальный момент времени поступают запросы:
· 5 вверх (7, 29, 46, 49, 50)
· 50 вниз (10, 28, 35, 45)
Когда лифт, среагировавший на запрос с 5-ого этажа, погрузил пассажиров и получил этажи назначения, производится запрос:
· 10 вверх (35, 45)
Когда лифт, среагировавший на запрос с 50-ого этажа, погрузил пассажиров и получил этажи назначения, производится запрос:
· 30 вниз (10)
Когда лифт, среагировавший на запрос с 10-ого этажа, погрузил пассажиров и получил этажи назначения, производится запрос:
· 47 вверх (50)
Хоть и превышение в скорости реакции на запрос, модели использующей набор правил №1 не существенно, пройденное лифтами расстояние примерно на 70% меньше.
Выводы из экспериментов
Модель, действующая по набору правил №1, даёт результаты, как минимум не хуже, чем результаты, получаемые от модели с набором правил №2. В ряде случаев даёт преимущество в пройденном расстоянии ~70% и времени ожидания ~60%. В последствии следует развивать модель с набором правил №1, введя в неё возможность сохранения запросов в порядке времени достижимости. Причём прилагаемый код программ может быть использован повторно.
Замечания по моделированию
Прилагаемая к данной работе реализация моделей использует STL языка С++ и корректно будет работать только если скомпилирована компилятором Microsoft Visual C++. Данные ограничения обусловлены, различиями в реализации STL различными разработчиками компиляторов. В свою очередь компилятор от Microsoft рекомендован разработчиками STL как корректно поддерживающий её.
|