Курсова робота
з дисциплини: Теорема ймовірності
на тему: Незалежні випробування
Введення
При практичному застосуванні теорії ймовірностей часто доводиться зустрічатися із задачами, у яких те саме випробування повторюється неодноразово. У результаті кожного випробування може з'явитися або не з'явитися деяка подія А, причому нас не цікавить результат кожного окремого випробування, а загальне число появ події А в результаті серії досвідів. Наприклад, якщо виробляється група пострілів по однієї й тій же меті, нас, як правило, не цікавить результат кожного пострілу, а загальне число влучень. У подібних задачах потрібно вміти визначати ймовірність будь-якого заданого числа появ події в результаті серії досвідів. Такі задачі й будуть розглянуті. Вони вирішуються досить просто у випадку, коли випробування є незалежними.
Визначення. Випробування називаються незалежними, якщо ймовірність того або іншого результату кожного з випробувань не залежить від того, які результати мали інші випробування.
Наприклад, кілька кидань монети являють собою незалежні випробування.
1
. Формула Бернуллі
Нехай зроблено два випробування(n=2). У результаті можливе настання одного з наступних подій: 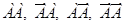
Відповідні ймовірності даних подій такі: 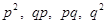 . .
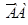 або або  - настання події тільки в одному випробуванні. - настання події тільки в одному випробуванні.
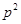 - імовірність настання події два рази. - імовірність настання події два рази.
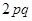 - імовірність настання події тільки один раз. - імовірність настання події тільки один раз.
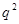 - імовірність настання події нуль раз. - імовірність настання події нуль раз.
Нехай тепер n=3. Тоді можливе настання одного з наступних варіантів подій:
 . .
Відповідні ймовірності рівні 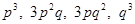 . .
Очевидно, що отримані результати при n=2 і n=3 є елементами
 и. и.
Тепер допустимо, зроблено n випробувань. Подія А може наступити n раз, 0 разів, n-1 раз і т.д. Напишемо подію, що складається в настанні події А m раз
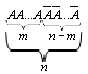
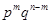
Необхідно знайти число випробувань, у яких подія А наступить m раз. Для цього треба знайти число комбінацій з n елементів, у яких А повторюється m раз, а 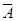 n-m раз. n-m раз.
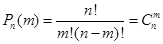
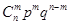 - імовірність настання події А. - імовірність настання події А.
 (1) (1)
Остання формула називається формулою Бернуллі і являє собою загальний член розкладання  : :
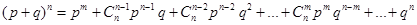 . .
З формули (1) видно, що її зручно використовувати, коли число випробувань не занадто велике.
Приклади
№1. Кидається монета 7 разів. Знайти ймовірність настання орла три рази.
Рішення.
n=7, m=3
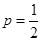
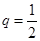
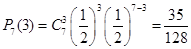 . .
№2. Щодня акції корпорації АВС піднімаються в ціні або падають у ціні на один пункт із ймовірностями відповідно 0,75 і 0,25. Знайти ймовірність того, що акції після шести днів повернуться до своєї первісної ціни. Прийняти умову, що зміни ціни акції нагору й долілиць - незалежні події.
Рішення. Для того, щоб акції повернулися за 6 днів до своєї первісної ціни, потрібно, щоб за цей час вони 3 рази піднялися в ціні й три рази опустилися в ціні. Шукана ймовірність розраховується по формулі Бернуллі
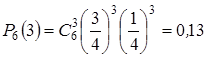
№3. Мотори багатомоторного літака виходять із ладу під час польоту незалежно один від іншого з імовірністю р. Багатомоторний літак продовжує летіти, якщо працює не менш половини його моторів. При яких значеннях р двомоторний літак надійніше чотиримоторного літака?
Рішення. Двомоторний літак терпить аварію, якщо відмовляють обоє його мотора. Це відбувається з імовірністю р2. Чотиримоторний літак терпить аварію, якщо виходять із ладу всі 4 мотори а це відбувається з імовірністю р4, або виходять із ладу три мотори з 4-х. Імовірність останньої події обчислюється по формулі Бернуллі: 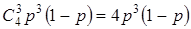 . Щоб двомоторний літак був надійніше, ніж чотиримоторний, потрібно, щоб виконувалася нерівність . Щоб двомоторний літак був надійніше, ніж чотиримоторний, потрібно, щоб виконувалася нерівність
р2<р4+4p3(1–p)
Ця нерівність зводиться до нерівності (3 р-р-1)( р-р-1)<0. Другий співмножник у лівій частині цієї нерівності завжди негативний (за умовою задачі). Отже, величина 3 р-р-1 повинна бути позитивної, звідки треба, що повинне виконуватися умову р>1/3. Слід зазначити, що якби ймовірність виходу з ладу мотора літака перевищувала одну третину, сама ідея використання авіації для пасажирських перевезень була б дуже сумнівною.
№4. Бригада з десяти чоловік іде обідати. Є дві однакові їдальні, і кожний член бригади незалежно один від іншого йде обідати в кожну із цих їдалень. Якщо в одну з їдалень випадково прийде більше відвідувачів, чим у ній є місць, то виникає черга. Яке найменше число місць повинне бути в кожній з їдалень, щоб імовірність виникнення черги була менше 0,15?
Рішення. Рішення задачі прийде шукати перебором можливих варіантів. Спочатку помітимо, що якщо в кожній їдальні по 10 місць, то виникнення черги неможливо. Якщо в кожній їдальні по 9 місць, то черга виникне тільки у випадку, якщо всі 10 відвідувачів потраплять в одну їдальню. З умови задачі треба, що кожний член бригади вибирає дану їдальню з імовірністю 1/2. Виходить, усі зберуться в одній їдальні з імовірністю 2(1/2)10=1/512. Це число багато менше, ніж 0,15, і варто провести розрахунок для їдалень. Якщо в кожній їдальні по 8 місць, то черга виникне, якщо всі члени бригади прийдуть в одну їдальню, імовірність цієї події вже обчислена, або 9 чоловік підуть в одну їдальню, а 1 чоловік вибере іншу їдальню. Імовірність цієї події розраховується за допомогою формули Бернуллі  . Таким чином, якщо в їдальнях по 8 місць, то черга виникає з імовірністю 11/512, що поки ще менше, ніж 0,15. Нехай тепер у кожній з їдалень по 7 місць. Крім двох розглянутих варіантів, у цьому випадку черга виникне, якщо в одну з їдалень прийде 8 чоловік, а в іншу 2 чоловік. Це може відбутися з імовірністю . Таким чином, якщо в їдальнях по 8 місць, то черга виникає з імовірністю 11/512, що поки ще менше, ніж 0,15. Нехай тепер у кожній з їдалень по 7 місць. Крім двох розглянутих варіантів, у цьому випадку черга виникне, якщо в одну з їдалень прийде 8 чоловік, а в іншу 2 чоловік. Це може відбутися з імовірністю 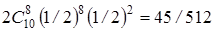 . .
Виходить, у цьому випадку черга виникає з імовірністю 56/512=0,109375<0,15. Діючи аналогічним образом, обчислюємо, що якщо в кожній їдальні 6 місць, то черга виникає з імовірністю 56/512+120/512=176/512=0,34375. Звідси одержуємо, що найменше число місць у кожній їдальні повинне рівнятися семи.
№5.В урні 20 білих і 10 чорних куль. Вийняли 4 кулі, причому кожну вийняту кулю повертають в урну перед добуванням наступні й кулі в урні перемішують. Знайти ймовірність того, що із чотирьох вийнятих куль виявиться 2 білих.
Рішення.ПодіяА– дістали білу кулю. Тоді ймовірності
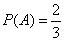 , ,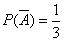 . .
По формулі Бернуллі необхідна ймовірність дорівнює
 . .
№6.Визначити ймовірність того, що в родині, що має 5 дітей, буде не більше трьох дівчинок. Імовірності народження хлопчика й дівчинки передбачаються однаковими.
Рішення.Імовірність народження дівчинки
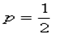 , тоді , тоді 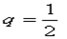 . .
Знайдемо ймовірності того, що в родині немає дівчинок, народилася одна, дві або три дівчинки:
бернуллі формула лаплас ймовірність
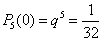 , ,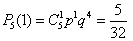 , ,
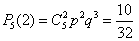 , ,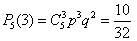 . .
Отже, шукана ймовірність
 . .
№7.Серед деталей, оброблюваних робітником, буває в середньому 4% нестандартні. Знайти ймовірність того, що серед узятих на випробування 30 деталей дві будуть нестандартними.
Рішення.Тут досвід полягає в перевірці кожної з 30 деталей на якість. Подія А - "поява нестандартної деталі", його ймовірність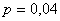 , тоді , тоді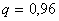 . Звідси по формулі Бернуллі знаходимо . Звідси по формулі Бернуллі знаходимо
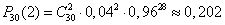 . .
№8.При кожному окремому пострілі зі знаряддя ймовірність поразки мети дорівнює 0,9. Знайти ймовірність того, що з 20 пострілів число вдалих буде не менш 16 і не більше 19.
Рішення.Обчислюємо по формулі Бернуллі:
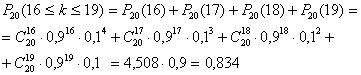
№9.Незалежні випробування тривають доти, поки подіяАне відбудетьсяkраз. Знайти ймовірність того, що буде потрібноnвипробувань (n і k), якщо в кожному з них . .
Рішення.ПодіяВ– рівноnвипробувань до k-го появи подіїА– є добуток двох наступних подій:
D – в n-ом випробуванніАвідбулося;
С – у перші(n–1)-ом випробуванняхАз'явилося(до-1)раз.
Теорема множення й формула Бернуллі дають необхідну ймовірність:
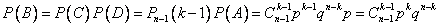 . .
№10.З n акумуляторів за рік зберігання k виходить із ладу. Вибирають m акумуляторів. Визначити ймовірність того, що серед них l справних n = 100, k = 7, m = 5, l = 3.
Рішення:Маємо схему Бернуллі з параметрами p=7/100=0,07 (імовірність того, що акумулятор вийде з ладу), n = 5 (число випробувань), k = 5-3 =2 (число "успіхів", несправних акумуляторів). Будемо використовувати формулу Бернуллі (імовірність того, що в n випробуваннях подія відбудеться k раз).
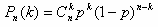
Одержуємо
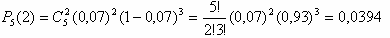
№11.Пристрій, що складається з п'яти незалежно працюючих елементів, включається за час Т. Імовірність відмови кожного з них за цей час дорівнює 0,2. Знайти ймовірність того, що відмовлять: а) три елементи; б) не менш чотирьох елементів; в) хоча б один елемент.
Рішення:Маємо схему Бернуллі з параметрами p = 0,2 (імовірність того, що елемент відмовить), n = 5 (число випробувань, тобто число елементів), k (число "успіхів", що відмовили елементів). Будемо використовувати формулу Бернуллі (імовірність того, що для n елементів відмова відбудеться в k елементах):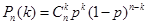 . Одержуємо а) . Одержуємо а)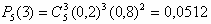 - імовірність того, що відмовлять рівно три елементи з п'яти.б) - імовірність того, що відмовлять рівно три елементи з п'яти.б)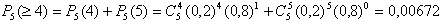 - імовірність того, що відмовлять не менш чотирьох елементів з п'яти (тобто або чотири, або п'ять). в) - імовірність того, що відмовлять не менш чотирьох елементів з п'яти (тобто або чотири, або п'ять). в)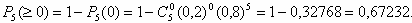 - імовірність того, що відмовить хоча б один елемент (знайшли через імовірність протилежної події - жоден елемент не відмовить). - імовірність того, що відмовить хоча б один елемент (знайшли через імовірність протилежної події - жоден елемент не відмовить).
№12.Скільки варто зіграти партій у шахи з імовірністю перемоги в одній партії, рівної 1/3, щоб число перемог було дорівнює 5?
Рішення: Число перемог k визначається з формули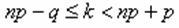 Тут p =1/3 (імовірність перемоги), q = 2/3 (імовірність програшу), n - невідоме число партій. Підставляючи даного значення, одержуємо: Тут p =1/3 (імовірність перемоги), q = 2/3 (імовірність програшу), n - невідоме число партій. Підставляючи даного значення, одержуємо:

Одержуємо, що n = 15, 16 або 17.
2
. Локальна формула Муавра-Лапласа
Легко бачити, що користуватися формулою Бернуллі при більших значеннях n досить важко, тому що формула вимагає виконання дій над величезними числами. Природно, виникає питання: чи не можна обчислити ймовірність, що цікавить нас,, не прибігаючи до формули Бернуллі.
В 1730 р. інший метод рішення при p=1/2 знайшов Муавр; в 1783 р. Лаплас узагальнив формулу Муавра для довільного p, відмінного від 0 і 1.
Ця формула застосовується при необмеженому зростанні числа випробувань, коли ймовірність настання події не занадто близька до нуля або одиниці. Тому теорему, про яку мова йде, називають теоремою Муавра-Лапласа.
Теорема Муавра-Лапласа. Якщо ймовірність p появи події А в кожному випробуванні постійне й відмінна від нуля й одиниці, то ймовірність  того, що подія А з'явиться в n випробуваннях рівно k раз, приблизно дорівнює(тим точніше, чим більше n) значенню функції того, що подія А з'явиться в n випробуваннях рівно k раз, приблизно дорівнює(тим точніше, чим більше n) значенню функції
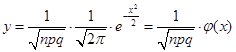
При 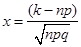 . .
Є таблиці, у яких поміщені значення функції
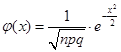 , ,
відповідним позитивним значенням аргументу x(див. додаток 1). Для негативних значень аргументу користуються тими ж таблицями, тому що функція 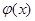 парна, тобто парна, тобто 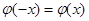 . .
Отже, імовірність того, що подія A з'явиться в n незалежних випробуваннях рівно k раз, приблизно дорівнює
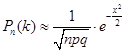 , ,
де 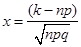 . .
№13. Знайти ймовірність того, що подія А наступить рівно 80 разів в 400 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,2.
Рішення. За умовою n=400; k=80; p=0,2; q=0,8. Скористаємося формулою Лапласа:
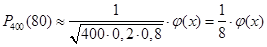 . .
Обчислимо обумовлене даними задачі значення x:
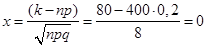 . .
По таблиці додатка 1 знаходимо 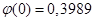 . .
Шукана ймовірність
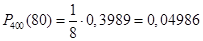 . .
№14. Імовірність поразки мішені стрільцем при одному пострілі p=0,75.
Знайти ймовірність того, що при 10 пострілах стрілок уразить мішень 8 разів.
Рішення. За умовою n=10; k=8; p=0,75; q=0,25.
Скористаємося формулою Лапласа:
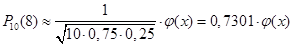 . .
Обчислимо обумовлене даними задачі значення x:
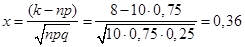 . .
По таблиці додатка 1 знаходимо
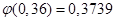
Шукана ймовірність
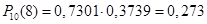 . .
№15. Знайти ймовірність того, що подія А наступить рівно 70 разів в 243 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,25.
Рішення. За умовою n=243; k=70; p=0,25; q=0,75. Скористаємося формулою Лапласа:
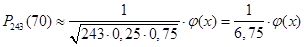 . .
Знайдемо значення x:
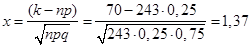 . .
По таблиці додатка 1 знаходимо
 . .
Шукана ймовірність
 . .
№16. Знайти ймовірність того, що подія А наступить 1400 разів в 2400 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює 0,6.
Рішення. За умовою n=2400; k=1400; p=0,6; q=0,4. Як і в попередньому прикладі, скористаємося формулою Лапласа:

Обчислимо x:
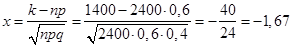 . .
По таблиці додатка 1 знаходимо
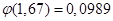
Шукана ймовірність
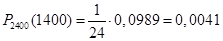 . .
3
. Формула Пуассона
Ця формула застосовується при необмеженому зростанні числа випробувань, коли ймовірність настання події досить близька до 0 або 1.
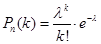 , ,
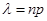 . .
Доказ.
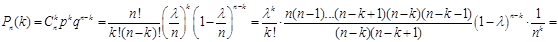
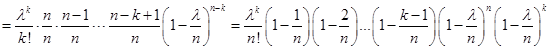 . .
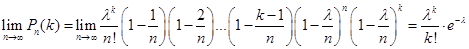 . .
У такий спосіб одержали формулу:
 . .
Приклади
№17. Імовірність виготовлення негідної деталі дорівнює 0,0002. Знайти ймовірність того, що серед 10000 деталей тільки 2 деталі будуть негідними.
Рішення. n=10000; k=2; p=0,0002. 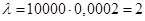
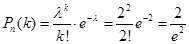 . .
№18. Імовірність виготовлення бракованої деталі дорівнює 0,0004. Знайти ймовірність того, що серед 1000 деталей тільки 5 деталі будуть бракованими.
Рішення. n=1000; k=5; p=0,0004.
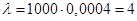
Шукана ймовірність
 . .
№19. Імовірність виграшу лотереї дорівнює 0,0001. Знайти ймовірність того, що з 5000 спроб виграти вдасться 3 рази.
Рішення. n=5000; k=3; p=0,0001.

Шукана ймовірність
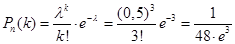 . .
4
. Теорема Бернуллі про частоту ймовірності
Теорема. Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність появи події дорівнює p, абсолютна величина відхилення відносної частоти появи події від імовірності появи події не перевищить позитивного числа 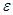 , приблизно дорівнює подвоєної функції Лапласа при , приблизно дорівнює подвоєної функції Лапласа при  : :
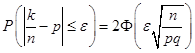 . .
Доказ. Будемо вважати, що виробляється n незалежних випробувань, у кожному з яких імовірність появи події А постійна й дорівнює p. Поставимо перед собою задачу знайти ймовірність того, що відхилення відносної частоти  від постійної ймовірності p по абсолютній величині не перевищує заданого числа від постійної ймовірності p по абсолютній величині не перевищує заданого числа 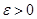 . Інакше кажучи, знайдемо ймовірність здійснення нерівності . Інакше кажучи, знайдемо ймовірність здійснення нерівності
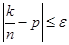 . (*) . (*)
Замінимо нерівність (*) йому рівносильними:
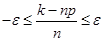 . .
Множачи ці нерівності на позитивний множник 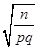 , одержимо нерівності, рівносильні вихідному: , одержимо нерівності, рівносильні вихідному:
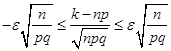 . .
Тоді ймовірність знайдемо в такий спосіб:
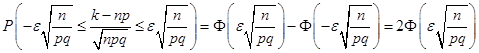 . .
Значення функції 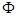 перебуває по таблиці(див. додаток 2). перебуває по таблиці(див. додаток 2).
Приклади
№20. Імовірність того, що деталь не стандартна, p=0,1. Знайти ймовірність того, що серед випадково відібраних 400 деталей відносна частота появи нестандартних деталей відхилиться від імовірності p=0,1 по абсолютній величині не більш, ніж на 0,03.
Рішення. n=400; p=0,1; q=0,9; 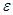 =0,03. Потрібно знайти ймовірність =0,03. Потрібно знайти ймовірність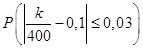 . Користуючись формулою . Користуючись формулою
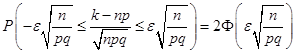 , ,
маємо
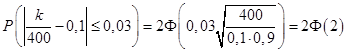 . .
По таблиці додатка 2 знаходимо 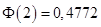 . Отже, . Отже, 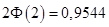 . Отже, шукана ймовірність дорівнює 0,9544. . Отже, шукана ймовірність дорівнює 0,9544.
№21. Імовірність того, що деталь не стандартна, p=0,1. Знайти, скільки деталей треба відібрати, щоб з імовірністю, рівної 0,9544, можна було затверджувати, що відносна частота появи нестандартних деталей(серед відібраних) відхилиться від постійної ймовірності p по абсолютній величині не більше ніж на 0,03.
Рішення. За умовою, p=0,1; q=0,9; 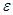 =0,03; =0,03; 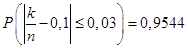 . Потрібно знайти n. Скористаємося формулою . Потрібно знайти n. Скористаємося формулою
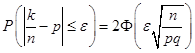 . .
У силу умови
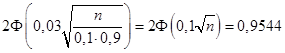
Отже,

По таблиці додатка 2 знаходимо 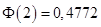 . Для відшукання числа n одержуємо рівняння . Для відшукання числа n одержуємо рівняння 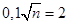 . Звідси шукане число деталей n=400. . Звідси шукане число деталей n=400.
№22. Імовірність появи події в кожному з незалежних випробувань дорівнює 0,2. Знайти, яке відхилення відносної частоти появи події від його ймовірності можна чекати з імовірністю 0,9128 при 5000 випробуваннях.
Рішення. Скористаємося тією же формулою, з якої треба:
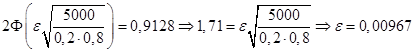 . .
Література
1. Гмурман Е.В. Теорія ймовірностей і математична статистика. – К., 2003
2. Гмурман Е.В. Керівництво до рішення задач по теорії ймовірностей і математичній статистиці. – К., 2004.
3. Гнеденко Б.В. Курс теорії ймовірностей. – К., 2007.
4. Колемаєв В.А., Калініна В.Н., Соловйов В.И., Малихин В.І., Курочкин О.П. Теорія ймовірностей у прикладах і задачах. – К., 2004.
5. Вентцель Е.С. Теорія ймовірностей. – К., 2004
Додат
ки
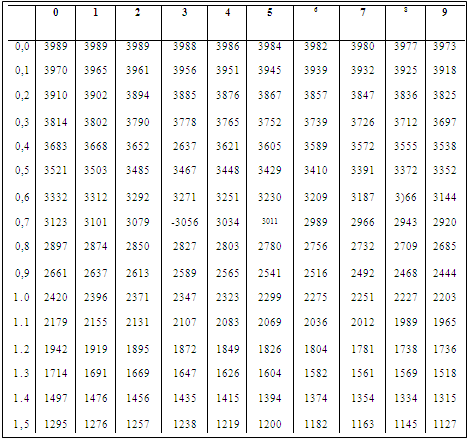
Додаток 1
Таблиця значень функції 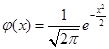
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1.6 |
1109 |
1092 |
1074 |
1057 |
1040 |
1023 |
1006 |
0989 |
0973 |
0957 |
| 1.7 |
0940 |
0925 |
0909 |
0893 |
0878 |
0863 |
0648 |
0833 |
0818 |
0804 |
| 1.8 |
0790 |
0775 |
0761 |
0748 |
0734 |
0721 |
0707 |
0694 |
0681 |
0669 |
| 1.9 |
0656 |
0644 |
0632 |
0620 |
0608 |
0596 |
0584 |
0573 |
0562 |
0551 |
| 2,0 |
0540 |
0529 |
0519 |
0508 |
0498 |
0488 |
0478 |
0468 |
0459 |
0449 |
| 2.1 |
0440 |
0431 |
0422 |
0413 |
0404 |
0396 |
0387 |
0379 |
0371 |
0363 |
| 2.2 |
0355 |
0347 |
0339 |
0332 |
0325 |
0317 |
0310 |
0303 |
0297 |
0290 |
| 2.3 |
0283 |
0277 |
0270 |
0264 |
0258 |
0252 |
0246 |
0241 |
0235 |
0229 |
| 2,4 |
0224 |
0219 |
0213 |
0208 |
0203 |
0198 |
0194 |
0189 |
0184 |
0180 |
| 2.5 |
0175 |
0171 |
0167 |
0163 |
0158 |
0154 |
0151 |
0147 |
0143 |
0139 |
| 2.6 |
0136 |
0132 |
0129 |
0126 |
0122 |
0119 |
0116 |
0113 |
0110 |
0107 |
| 2,7 |
0104 |
0101 |
0099 |
0096 |
0093 |
0091 |
0088 |
0086 |
0084 |
0081 |
| 2,8 |
0079 |
0077 |
0075 |
0073 |
0071 |
0069 |
0067 |
0065 |
0063 |
0061 |
| 2.9 |
0060 |
0058 |
0056 |
0055 |
0053 |
0051 |
0050 |
0048 |
0047 |
0043 |
| 3,0 |
0044 |
0043 |
0042 |
0040 |
0039 |
0038 |
0037 |
0036 |
0035 |
0034 |
| 3,1 |
0033 |
0032 |
0031 |
0030 |
0029 |
0028. |
0027 |
0026 |
0025 |
0025 |
| 3,2 |
0024 |
0023 |
0622 |
0022 |
0021 |
0020 |
0020 |
0019 |
0018 |
0018 |
| 3,3 |
0017 |
0017 |
0016 |
0016 |
0015 |
0015 |
0014 |
0014 |
0013 |
0013 |
| 3,4 |
0012 |
0012 |
0012 |
0011 |
0011 |
0010 |
0010 |
0010 |
0009 |
0009 |
| 3,5 |
0009 |
0008 |
0008 |
0008 |
0008 |
0007 |
0007 |
0007 |
0007 |
0006 |
| 3,6 |
0006 |
0006 |
0006 |
0005 |
0005 |
0005 |
0005 |
0005 |
0005 |
0004 |
| 3,7 |
0004 |
0004 |
0004 |
0004 |
0004 |
0004 |
0003 |
0003 |
0003 |
0003 |
| 3,8 |
0003 |
0003 |
0003 |
0003 |
0003 |
0002 |
0002 |
0002 |
0002 |
0002 |
| 3,9 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0001 |
0001 |
Додаток 2
Таблиця значень функції 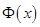
| x |
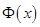 |
x |
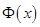 |
x |
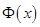 |
x |
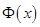 |
| 0900 |
0,0000 |
0,32 |
0,1255 |
0,64 |
0,2389 |
0,96 |
0,3315 |
| 0,01 |
0,0040 |
0,33 |
0,1293 |
0,65 |
0,2422 |
0,97 |
0,3340 |
| 0,02 |
0,0080 |
0,34 |
0,1331 |
0,66 |
0,2454 |
0,98 |
0,3365 |
| 0,03 |
0,0120 |
0,35 |
0,1368 |
0,67 |
0,2486 |
0.99 |
0,3389 |
| 0,04 |
0,0160 |
0,36 |
0,1406 |
0,68 |
0,2517 |
1,00 |
0,3413 |
| 0,05 |
0,0199 |
0,37 |
0,1443 |
0,69 |
0,2549 |
1,01 |
0,3438 |
| 0,06 |
0,0239 |
0,38 |
0,1480 |
0,70 |
0,2580 |
1,02 |
0,3461 |
| 0,07 |
0,0279 |
0,39 |
0,1517 |
0,71 |
0,2611 |
1,03 |
0,3485 |
| 0,08 |
0,0319 |
0,40 |
0,1554 |
0,72 |
0,2642 |
1,04 |
0,3508 |
| 0,09 |
0,0359 |
0,41 |
0,1591 |
0,73 |
0,2673 |
1,05 |
0,3531 |
| 0,10 |
0,0398 |
0,42 |
0,1628 |
0,74 |
0,2703 |
1,06 |
0,3554 |
| 0,11 |
0,0438 |
0,43 |
0,1664 |
0,75 |
0,2734 |
1,07 |
0,3577 |
| 0,12 |
0,0478 |
0,44 |
0,1700 |
0,76 |
0,2764 |
1,08 |
0,3599 |
| 0,13 |
0,0517 |
0,45 |
0,1736 |
0,77 |
0,2794 |
1.09 |
0,3621 |
| 0,14 |
0,0557 |
0,46 |
0,1772 |
0,78 |
0,2823 |
1.10 |
0,3643 |
| 0,15 |
0,0596 |
0,47 |
0,1808 |
0,79 |
0,2852 |
3665 |
0,3665 |
| 0,16 |
0,0636 |
0,48 |
0,1844 |
0,80 |
0,2881 |
3686 |
0,3686 |
| 0,17 |
0,0675 |
0,49 |
01879 |
0,81 |
0,2910 |
1,13 |
0,3708. |
| 0,18 |
0,0714 |
0,50 |
0,1915 |
0,82 |
0,2939 |
1,14 |
0,3729 |
| 0,19 |
0,0753 |
0,51 |
0,1950 |
0,83 |
0,2967 |
1,15 |
0,3749 |
| 0,20 |
0,0793 |
0,52 |
0,1985 |
0,84 |
0,2995 |
1,16 |
0,3770 |
| 0,21 |
0,0832 |
0,53 |
0,2019 |
0,85 |
0,3023 |
1,17 |
0,3790 |
| 0,22 |
0,0871 |
0,54 |
0,2054 |
0,86 |
0,3051 |
1,18 |
0,3810 |
| 0,23 |
0,0910 |
0,55 |
0,2088 |
0,87 |
0,3078 |
1,19 |
0,3830 |
| 0,24 |
0,0948 |
0,56 |
0,2123 |
0,88 |
0,3106 |
1,20 |
0,3849 |
| 0,25 |
0,0987 |
0,57 |
0,2157 |
0,89 |
0,3133 |
1.21 |
0,3869 |
| 0,26 |
0,1026 |
0,58 |
0,2190 |
0,90 |
0,3159 |
1,22 |
0/3883 |
| 0,27 |
0,1064 |
0,59 |
0,2224 |
0,91 |
0,3186 |
1,23 |
0,3907 |
| 0,28 |
0,1103 |
0,60 |
0,2257 |
0,92 |
0,3212 |
1.24 |
0,3925 |
| 0,29 |
0,1141 |
0,61 |
0,2291 |
0,93 |
0,3238 |
1,25 |
0,3944 |
| 0,30 |
0,1179 |
0,62 |
0,2324 |
0,94 |
0,3264 |
| 0,31 |
0,1217 |
0,63 |
0,2357 |
0,95 |
0,3289 |
x
|
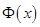 |
x |
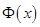 |
x |
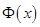 |
x |
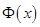 |
| 1,26 |
0,3962 |
1,59 |
0,4441 |
1,92 |
0,4726 |
2,50 |
0,4938 |
| 1,27 |
0,3980 |
1,60 |
0,4452 |
1,93 |
0,4732 |
2,52 |
0,4941 |
| 1,28 |
0,3997 |
1,61 |
0,4463 |
1,94 |
0,4738 |
2,54 |
0,4945 |
| 1,29 |
0.4015 |
1,62 |
0,4474 |
1,95 |
0,4744 |
2,56 |
0,4948 |
| 1,30 |
0,4032 |
1,63 |
0.4484 |
1.96 |
0,4750 |
2,58 |
0,4951 |
| 1,31 |
0,4049 |
1,64 |
0,4495 |
1,97 |
0,4756 |
2,60 |
0,4953 |
| 1,32 |
0.4066 |
1,65 |
0,4505 |
1,98 |
0,4761 |
2,62 |
0,4956 |
| 1,33 |
0,4082 |
1,66 |
0,4515 |
1,99 |
0,4767 |
2,64 |
0,4959 |
| 1,34 |
0.4099 |
1,67 |
0.4525 |
2.00 |
0,4772 |
2,66 |
0,4961 |
| 1.3S |
0.4115 |
1,68 |
0,4535 |
2,02 |
0,4783 |
2,68 |
0,4963 |
| 1,36 |
0.4131 |
1,69 |
0,4545 |
2,04 |
0,4793 |
2,70 |
0,4965 |
| 1,37 |
0.4147 |
1,70 |
0,4554 |
2,06 |
0,4803 |
2,72 |
0,4967 |
| 1,38 |
0.4162 |
1.71 |
0,4564 |
2,08 |
0,4812 |
2,74 |
0,4969 |
| 1,39 |
0.4177 |
1,72 |
0,4573 |
2,10 |
0,4821 |
2,76 |
0,4971 |
| 1.40 |
0,4192 |
1,73 |
0,4582 |
2,12 |
0,4830 |
2,78 |
0,4973 |
| 1.41 |
0,4207 |
1.74 |
0,4591 |
2,14 |
0,4838 |
2,80 |
0,4974 |
| 1.42 |
0.4222 |
1,75 |
0.4599 |
2,16 |
0,4846 |
2,82 |
0,4976 |
| 1.43 |
0.4236 |
1,76 |
0,4608 |
2,18 |
0,4854 |
2,84 |
0,4977 |
| 1.44 |
0,4251 |
1.77 |
0,4616 |
2,20 |
0,4861 |
2,86 |
0,4979 |
| 1,45 |
0.4265 |
1,78 |
0.4625 |
2,22 |
0,4868 |
2,88 |
0,4980 |
| 1.46 |
0,4279 |
1,79 |
0,4633 |
2,24 |
0,4875 |
2,90 |
0,4981 |
| 1.47 |
0,4292 |
1,80 |
0,4641 |
2,26 |
0,4881 |
2,92 |
0,4982 |
| 1,48 |
0,4306 |
1.81 |
0,4649 |
2,28 |
0,4887 |
2,94 |
0,4984 |
| 1,49 |
0.4319 |
1,82 |
0,4656 |
2,30 |
0,4893 |
2,96 |
0,4985 |
| 1.50 |
0,4332 |
1,83 |
0,4664 |
2,32 |
0,4898 |
2.98 |
0,4986 |
| 1,51 |
0,4345 |
1,84 |
0,4671 |
2,34 |
0,4904 |
3,00 |
0,49865 |
| 1.52 |
0,4357 |
1,85 |
0,4678 |
2,36 |
0,4909 |
3,20 |
0,49931 |
| 1.53 |
0,4370 |
1,86 |
0,4686 |
2,38 |
0,4913 |
3.40 |
0,49966 |
| 1.54 |
0,4382 |
1,87 |
0,4693 |
2,40 |
0,4918 |
3,60 |
0,49984 |
| 1,55 |
0,4394 |
1.88 |
0,4699 |
2,42 |
0,4922 |
3,80 |
0,49992 |
| 1.S6 |
0,4406 |
1.89 |
0,4706 |
2,44 |
0,4927 |
4,00 |
0,49996 |
| 1,57 |
0,4418 |
1,90 |
0,4713 |
2,46 |
0,4931 |
4,50 |
0,49999 |
| 1,58 |
0,4429 |
1,91 |
0,4719 |
2,48 |
0,4934 |
5,00 |
0,49999 |
|