СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ
1. Основні поняття і теореми
Постановка задачі.
Потрібно знайти значення х
1, х
2, … , хn
, що задовольняють таким співвідношенням:  .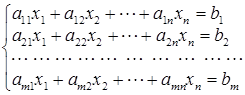
Тут aij
(i
= 1, 2, … , m
; j
= 1, 2, … , n
) і bk
(k
= 1, 2, … , m
) – задані числа.
При цьому: ;  ;  .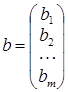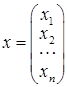
Матриця А
називається головною матрицею системи, вектор b
– вектором-стовпцем правих частин, вектор x
– вектором-стовпцем невідомих.
Використовуючи ці позначки, можна систему записати в матричній формі: Ах
= b
.
Якщо b
1 = b
2 = ¼ = bm
= 0, то система рівнянь називається однорідною
. Якщо хоча б одне з bk
(k
= 1, 2, ¼ , m
) відмінне від нуля, то система називається неоднорідною
.
 .
Матриця  називається розширеною матрицею
системи.
Якщо система має хоча б один розв’язок, то вона називається сумісною
.
При цьому система, що має єдиний розв’язок, називається визначеною
, а більше одного розв’язку – невизначеною
.
Якщо система не має розв’язків, то вона називається несумісною
.
При розв’язуванні систем лінійних рівнянь має бути знайдена відповідь на три запитання:
А. Чи сумісна система?
В. Чи визначена система?
С. Як знайти розв’язок (чи розв’язки) системи, якщо вони існують?
Правило Крамера.
Якщо неоднорідна система рівнянь невироджена (detА
¹ 0), то система визначена, тобто має єдиний розв’язок, і його можна знайти за формулами Крамера:  (k
= 1, 2, … , n
) де Dk
– визначник матриці, яку можна одержати, якщо в матриці А
системи k-
й стовпець замінити на стовпець вільних членів.
Ранг матриці.
З розв’язуванням систем рівнянь безпосередньо пов'язане поняття рангу матриці. Ранг матриці
– це найвищий порядок її мінора, відмінного від нуля.
Для того щоб знайти ранг матриці, важливо орієнтуватися в тому, які перетворення з матрицею можна робити, не змінюючи при цьому її ранг:
1) транспонування;
2) перестановка двох рядків (стовпців);
3) множення всіх елементів рядка (або стовпця) на число a¹ 0;
4) додавання до всіх елементів рядка (стовпця) відповіднихелементів іншого рядка (стовпця);
5) вилучення нульового рядка (стовпця);
6) викреслення рядка (стовпця), що є лінійною комбінацією інших рядків (стовпців).
Однорідні системи.
Розглядається однорідна система лінійних рівнянь з n
невідомими: Ах
= 0.
Якщо rangА
= n
(detА
¹ 0), то система визначена і має тільки тривіальний розв’язок: x
1 = x
2 = … = xn
= 0.
Якщо rangА
< n
(detА
= 0), то система має не тільки тривіальні розв’язки. При цьому всі розв’язки однорідної системи рівнянь утворюють лінійний простір L
і dim L
= n
– rangА
.
Щоб знайти базис простору розв’язків однорідної системи рівнянь, треба:
1.Знайти базисний мінор матриці А
.
2.Якщо рядок не входить до базисного мінора, то рівняння, яке йому відповідає, є лінійною комбінацією інших рівнянь, і його можна не брати до уваги.
3.Якщо стовпець не входить у базисний мінор, то невідома з відповідним номером призначається вільною. Усього знайдеться (n
– rang A
) вільних невідомих.
4.Нехай вільні невідомі хr
+1, хr
+2, … , хn
. Якщо дати вільним невідомим довільні значення, то одержимо неоднорідну систему рівнянь відносно хr
+1, хr
+2, … , х
n
, у якої визначник не дорівнює нулю, і, отже, система має єдиний розв’язок.
5.Дамо вільним невідомим значення (1, 0, 0, 0, … , 0), потім (0, 1, 0, 0, … , 0) і т. д. Розв’язуючи системи, що утворюють, одержимо відповідно вектори  . Ці вектори й утворюють базис простору L
розв’язків однорідної системи лінійних рівнянь.
6.Загальний розв’язок лінійної системи однорідних рівнянь у цьому випадку є лінійною комбінацією базисних векторів:
 .
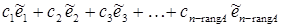Неоднорідні системи.
Теорема Кронекера – Капеллі: система неоднорідних лінійних рівнянь Ах
= b
сумісна тоді і тільки тоді, коли rangА
= rang .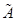
При цьому якщо rangА
= rang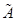= n
, то система має єдиний розв’язок і він може бути знайдений за правилом Крамера.
Якщо rangА
= rang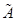<n
, то система має нескінченно багато розв’язків, які утворюють лінійний многовид. При цьому підпростір зсуву – це простір L
розв’язків однорідної системи рівнянь, і його базис можна побудувати способом, який було розглянуто вище. Вектор зсуву – це частинний розв’язок неоднорідної системи рівнянь. і він може бути знайдений, якщо в неоднорідній системі вільні невідомі покласти рівними деяким довільним значенням (наприклад, нульовим).
Загальний розв’язок неоднорідної системи – це загальний розв’язок відповідної однорідної системи плюс деякий частинний розв’язок неоднорідної системи. Останнє твердження можна записати через абревіатури відповідних термінів: З.Р.Н.С. = З.Р.О.С. + Ч.Р.Н.С.
Обернена матриця
.
Запишемо систему в матричному вигляді Ах
= b
. Якщо detА
¹ 0 (така матриця А
називається невиродженою
), то для матриці А
існує матриця А
–1 така, що А
–1А
= АА
–1 = Е
.Така матриця називається оберненою
до матриці А
, і розв’язок системи можна записати за допомогою оберненої матриці у вигляді: А
–1Ах
= А
–1b
Þх
= А
–1b
.
Таким чином, у випадку існування оберненої матриці А
–1розв’язок системи має вигляд: х
= А
–1b
.
Як же знайти обернену матрицю А
–1 до невиродженої матриці А
?
I спосіб.
1)
Складемо матрицю Аik
з алгебраїчних доповнень до елементів аik
матриці А
;
2) транспонуємо матрицю з алгебраїчних доповнень;
3) кожен елемент матриці, що утворилась, ділимо на detА
.
В результаті маємо обернену матрицю –
А-1.
II спосіб.
1) Запишемо матрицю А
, а праворуч від неї, через вертикальну риску, –одиничну матрицю Е
. Одержимо матрицю яка має n
рядків та 2n
стовпців;
2) у матриці, що утворилась, за допомогою застосування до рядків (і тільки до рядків) перетворень, що не змінюють ранг матриці, утворимо на місці матриці А
одиничну матрицю.
На місці одиничної матриці тепер стоїть А
–1.
III спосіб.
Праворуч від матриці припишемо одиничну матрицю Е
, а знизу припишемо матрицю (–Е
). У правому нижньому куті поставимо нульову матрицю. Використовуючи операції тільки над рядками матриці, що утворилась, на місці матриці (–Е
) утворимо нульову матрицю. Тоді у правому нижньому куті буде стояти А
–1.
IV спосіб.
Для обернення матриці, що має блокову структуру, тобто матриці вигляду: 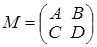 , де А
– квадратна матриця порядку n
´n
, а D
– квадратна матриця q
´q
, справедливі дві формули Фробеніуса:
1.Перша формула Фробеніуса
(якщо detА
¹ 0):
 , де H
= D
– CA
–1B
.
2.Друга формула Фробеніуса
(якщо detD
¹ 0):
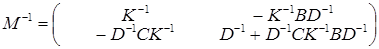 , де K
= A
– BD
–1C
.
2. Контрольні питання і завдання
1. Що таке ранг матриці і її базисний мінор? Чи визначаються вони однозначно?
2. Знайти ранг і всі базисні мінори матриці:  .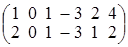
3. Як пов'язані ранг матриці і вимірність лінійної оболонки її рядків.
4. Чому дорівнює вимірність простору розв’язків однорідної системи лінійних рівнянь, якщо в системі 10 рівнянь, 16 невідомих і ранг матриці системи дорівнює 6?
5. Чи утворює множина розв’язків неоднорідної системи лінійний простір? Яка з властивостей лінійного простору не виконується?
6. Згадайте визначення лінійного многовиду. Що називається його базисом і вимірністю?
7. Як визначається вектор зсуву для лінійного многовиду, що є множиною розв’язків неоднорідної системи?
3. Приклади розв’язування задач
Задача 1.
Знайти ранг матриці  .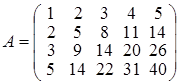
Розв’язання.
Насамперед відзначимо, що четвертий рядок матриці є сумою другого і третього рядків і тому при вилученні цього рядка ранг матриці не зміниться.
1.Відкинемо четвертий рядок.
2.З другого і третього рядків матриці віднімемо перший рядок, помножений, відповідно, на 2 та 3.
3.В отриманій матриці з третього рядка віднімемо другий, помножений на 2.
Одержимо ланцюжок перетворень:
лінійний рівняння матриця
 .
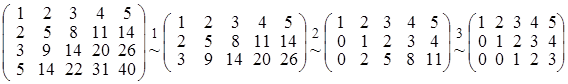У матриці, що утворилась, мінор, який стоїть в перших трьох стовпцях, не дорівнює нулю. Отже, ранг вихідної матриці дорівнює 3 і мінор 3-го порядку, що стоїть в перших трьох стовпцях, є базисним мінором матриці А.
Задача 2.
Знайти матрицю, яка є оберненою до матриці
 .
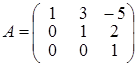Розв’язання.
Знайдемо обернену матрицю за визначенням. Нехай обернена матриця має вигляд: 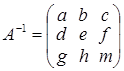 . Тоді, за визначенням,
АА
–1 = Е
, тобто  .
Знаходячи добуток матриць, одержимо рівності:
 .
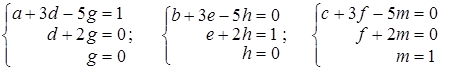Із цих співвідношень одержуємо: g
= 0, d
= 0, a
= 1; далі: h
= 0, e
=1, b
= –3. І нарешті: m
= 1, f
= –2, c
= 11. У підсумку дійдемо висновку, що:
 .
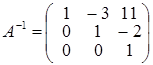Задача 3.
Знайти матрицю, яка є оберненою до матриці  .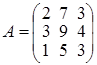
Розв’язання.
Побудуємо матрицю 6 ´ 6, дописавши праворуч від А
одиничну матрицю Е
, внизу матрицю (– Е
), а інші місця заповнимо нулями.
 .
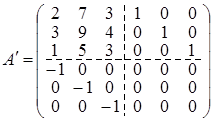За допомогою операцій над рядками матриці А
¢ утворимо на місці (–Е
) нульову матрицю. Тоді в правому нижньому куті буде стояти матриця А
–1.
1.До всіх рядків матриці А
¢ додамо третій рядок з деяким множником, домагаючись того, щоб всі елементи першого стовпця, крім а
31, дорівнювали нулю.
2.Перший рядок отриманої матриці поділимо на (–3) і, додаючи до інших рядків матриці отриманий перший рядок з деякими множниками, досягаємо того, щоб у другому стовпці стояли нулі, крім елемента а
12.
3.За допомогою другого рядка утворимо нулі в третьому стовпці, крім елемента а
23.
Одержимо ланцюжок перетворень:
 
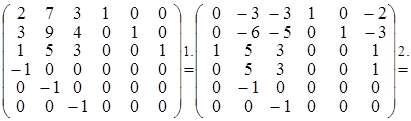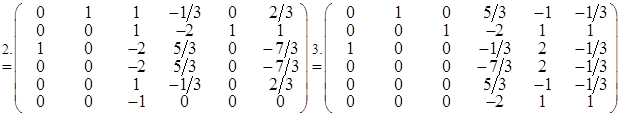
Звідси укладаємо, що  .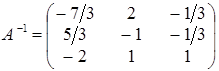
Задача 4.
Знайти матрицю, яка є оберненою до  .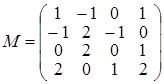
Розв’язання.
Для обернення матриці застосуємо першу формулу Фробеніуса. Позначимо:  ,  ,  ,  .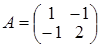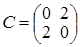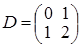
Знаходимо послідовно:
 ;
 ;
 ;
 .
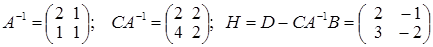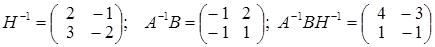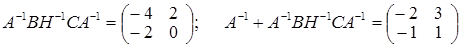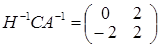І тоді 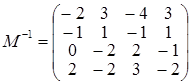 . Привабливість зазначеного способу полягає в тому, що для обернення матриці 4-го порядку ми маємо справу з оберненням матриць лише 2-го порядку, що істотно простіше.
Задача 5.
За допомогою правила Крамера розв’язати систему лінійних неоднорідних рівнянь:  .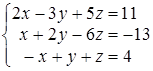
Розв’язання.
Головна матриця системи має вигляд:  .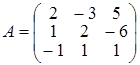
Розв’язок системи може бути знайдений за правилом Крамера, тому що detА
= D = 18 ¹ 0. Для цього побудуємо визначники Dх
, Dу
, Dz
, які відрізняються від головного визначника тим, що в ньому стовпець коефіцієнтів при, відповідно, х
, у
та z
замінено на стовпець вільних членів, тобто:
 .
Обчислюючи їх, знаходимо, що Dх
= 18, Dу
= 36, Dz
= 54.
Отже  .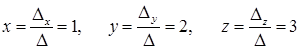
Задача 6.
Розв’язати систему лінійних однорідних рівнянь:
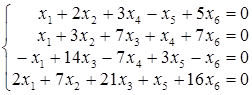
Розв’язання.
Насамперед відзначимо, що система напевне сумісна, оскільки однорідна система завжди має щонайменше нульовий розв’язок.
Почнемо пошук загального розв’язку даної системи. Головна матриця системи має вигляд:  .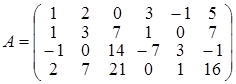
Знайдемо ранг матриці А.
Перший рядок матриці з відповідними множниками додамо до інших рядків матриці так, щоб елементи першого стовпця обернулися на нуль, крім елемента а
11. Вийде матриця А
1 така, що
rangА
1 = rangА
і  .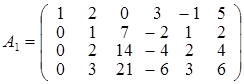
Відзначаючи, що третій і четвертий рядки матриці пропорційні другому рядку, укладаємо, що rangА
1 = rangА
2, де 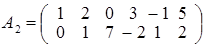 . Помножимо другий рядок матриці А
2 на (–2) і додамо до першого рядка. Одержимо матрицю А3: 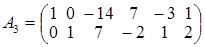 , таку, що rangА
3 = rangА
2 = 2. У підсумку rangА
= rangА
3 = 2.
Тоді вийшла система двох рівнянь, з яких можна написати:
х
1 = 14х
3 – 7х
4 + 3х
5 – х
6, х
2 = –7х
3 + 2х
4 – х
5 – 2х
6 і змінні х
3, х
4, х
5, х
6 – будь-які. Це і є розв’язок системи.
Однак можна (і необхідно) піти далі. Множина розв’язків лінійної однорідної системи утворює лінійний простір L
вимірності dimL
= n
– rangА
= 6 – 2 = 4. Для знаходження базисних векторів простору розв’язків надамо вільним невідомим х
3, х
4, х
5, х
6 значення: а) 1, 0, 0, 0; б) 0, 1, 0, 0; в) 0, 0, 1, 0; г) 0, 0, 0, 1. Одержимо чотири вектори, що утворять базис L
: е
1 = (14, –7, 1, 0, 0, 0); е
2 = (–7, 2, 0, 1, 0, 0); е
3 = (3, –1, 0, 0, 1, 0); е
4 = (–1, –2, 0, 0, 0, 1). У такий спосіб L
= ℒ(е
1, е
2, е
3, е
4), і будь-який розв’язок вихідної системи може бути записаний у вигляді лінійної комбінації базисних векторів, тобто у вигляді: с
1(14, –7, 1, 0, 0, 0) + с
2(–7, 2, 0, 1, 0, 0) + с
3(3, –1, 0, 0, 1, 0) + с
4(–1, –2, 0, 0, 0, 1), де с
1, с
2, с
3, с
4 – будь-які значення. Це і є загальний розв’язок вихідної лінійної однорідної системи рівнянь.
Задача 7.
Розв’язати систему лінійних неоднорідних рівнянь
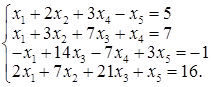
Розв’язання.
Розширена матриця системи рівнянь має вигляд:  , причому до вертикальної риски записана головна матриця системи, а після вертикальної риски – стовпець вільних членів. Перетворюючи матрицю 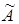 аналогічно до того, як перетворювалася матриця А
в розв’язку попередньої задачі, одержимо матрицю А
таку, що rang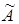 = rangА
= 2 і 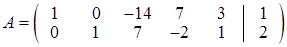 . Звідси можна записати загальний розв’язок системи у вигляді: х
1 = 1 + 14х
3 – 7х
4 – 3х
5, х
2 = 2 – 7х
3 + 2х
4 – х
5, де х
3, х
4, х
5 – будь-які.
Це і є загальний розв’язок вихідної системи лінійних рівнянь. Однак з метою прояснення алгебраїчної структури розв’язку системи відзначимо таке:
Враховуючи, що rang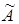 = rang A
= 2 < n
= 5, можемо зазначити, що множина розв’язків системи являє собою лінійний многовид. Вектором зсуву цього лінійного многовиду є частинний розв’язок неоднорідної системи рівнянь, для знаходження якого дамо вільним невідомим х
3, х
4, х
5 довільні значення (наприклад нулі) і одержимо: f
= (1, 2, 0, 0, 0). Підпростором зсуву є простір розв’язків однорідної системи з матрицею А
2, яка збігається з головною матрицею вихідної системи неоднорідних рівнянь
 .
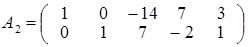Звідси х
1 = 14х
3 – 7х
4 – 3х
5, х
2 = – 7х
3 + 2х
4 – х
5, де х
3, х
4, х
5 – будь-які. Даючи вільним змінним х
3, х
4, х
5 значення: а) 1, 0, 0; б) 0,1,0; в) 0, 0, 1; одержимо, відповідно, базисні вектори простору L
розв’язків однорідної системи рівнянь:е
1 = (14, –7, 1, 0, 0), е
2 = (–7, 2, 0, 1, 0), е
3 = (–3, –1, 0, 0, 1).
Отже, розв’язки вихідної системи утворюють лінійний многовид М
:
M
= {x
½x
= f
+ c
1e
1 + c2e2
+ c
3e
3}, де c
1, c2
, c
3 – будь-які,
|
