Курсовая работа
«Численные методы в экономике»
Тема:
«Итерационный метод решения проблемы собственных значений»
Новосибирск
, 2010
Введение
В данной курсовой работе рассмотрен итерационный метод решения проблемы собственных значений. Сходимость итерационного процесса может быть очень медленной. Причиной этого является наличие нелинейного элементарного делителя, соответствующего первому собственному числу. Другая причина – это близость второго собственного числа к первому. В этом случае можно ускорить сходимость несколькими методами. Одним из них является метод скалярных произведений, который рассмотрен в данной работе.
В методе скалярных произведений число итераций, необходимых для определения максимального собственного числа матрицы, с данной точностью, сокращается почти вдвое.
математический итерационный метод программный
1.
Математическая постановка задачи
Этот метод особенно удобен в применении к симметричной матрице, однако попробуем изложить его без этого предположения. В основе метода лежат последовательности итераций вектора Y0
матрицами A и A’, транспонированной с А. Эти последовательности имеют следующий вид:
Y0
, Y1
=A*Y0
, Y2
=A2
*Y0
, …, Yk
=Ak
*Y0
, … (1)
Y0
, Y’1
=A’*Y0
, Y’2
=A’2
*Y0
, …, Y’k
=A’k
*Y0
, … (2)
Пусть b1
, …, bn
координатывектора Y0
вбазисе X’1
, …, X’n
, a1
, …, an
координаты Y0
вбазисе X1
, …, Xn
. При этом предположим, что базисы выбраны так, что система векторов X1
, X2
, …, Xn
и X’1
, …, X’n
удовлетворяет условиям ортогональности и нормированности.
Образуем скалярное произведение (Y’k
, Yk
):
(Y’k
, Yk
)=(A’k
*Y0
, Ak
*Y0
)=(Y0
, A2k
*Y0
)=(b1
*X’1
+ … +bn
*X’n
, a1
*l2k
1
*X1
+ … + + an
*l2k
n
*Xn
)
Далее в силу свойств ортогональности и нормированности системы векторов имеем:
(Y’k
, Yk
)=a1
*b1
*l2k
1
+ … + an
*bn
*l2k
n
(3).
Аналогично:
(Y’k-1
, Yk
)=a1
*b1
*l2k-1
1
+ … + an
*bn
*l2k-1
n
(4).
Можно видеть, что из равенств (3) и (4) получаем:
(Y’k
, Yk
)/(Y’k
-1
, Yk
) = l1
+ O(l2
/l1
)2
k
.
Из этой оценки видно, что образование скалярного произведения сокращает число шагов итераций, нужных для определения максимального собственного l1
, с данной точностью, почти вдвое. Однако при этом требуется дополнительное вычисление последовательности (2).
Следует отметить, что в случае симметричной матрицы, последовательности (1) и (2) совпадают, и поэтому в этом случае применение метода скалярного произведения особенно целесообразно. Начиная с некоторого шага итерации, нужно вычислять соответствующие скалярные произведения и определять l1
через их отношения.
Программа, реализующая рассматриваемый метод, разработана в среде МаtLab, предназначенной для выполнения математических операций. Она состоит из головной программы и 2х подпрограмм, вызываемых из основной программы.
Головная программа (main.m)
В основной программе задается начальное приближение yn,
начальное значение собственного вектора L1
и значение допустимой ошибки ed.
Текст программы:
clc %очистка экрана
yn=[1; 1; 1; 1]; %задание начального приближения собственного вектора
L1=-5.5251;%начальное значение собственного числа матрицы
ed=0.00001; %значение допустимой ошибки
trace=1; %установка режима вывода на экран
[mout, Lout, yout]=sobstv ('fun', yn, L1, ed, trace);%вызов функции, реализующей метод скалярных произведений
plot (mout, Lout) %вывод графика значений собственного числа заданной матрицы за время итерационного процесса
pause;
plot (mout, yout)%вывод графика значений собственного вектора, соответствующего собственному числу
Подпрограмма sobstv.m
В данной подпрограмме происходит вычисление максимального собственного числа и соответствующего ему собственного вектора. Значение собственного числа на каждом шаге заносится в L,
результат умножения матрицы а
на заданный вектор заносится в yn.
Время выполнения итераций равно t,
количество итераций –m
.
Текст программы:
function [mout, Lout, yout]=sobstv (fun, yn, L1, ed, trace);
a=feval(fun);%вызов матрицы, описанной в файле с именем matrsp
m=0; %обнуление счетчика итераций
Lout=L1; mout=m; yout=yn';
L=0; %присваивание начального значения решения
iftrace
clc, yn, m, L1% вывод значения решений на данном этапе
end
t0=fix(clock); %задание начальной точки отсчета времени выполнения итераций
while (abs (L1-L)>ed) %задание цикла
yn1=yn;
yn=a*yn;
L=L1;
L1=(yn'*yn)/(yn1'*yn); %вычисление собственного числа
y=yn/sqrt (yn'*yn);%вычисление собственного вектора
iftrace
home, y, m, L1%вывод текущих значений на экран
end %на данном этапе итераций
m=m+1;%увеличение счетчика итераций
Lout=[Lout; L1]; %формирование выходных параметров
mout=[mout; m];
yout=[yout; y'];
end
t1=fix(clock); %значение конечного момента времени
t=t1-t0%время выполнения итераций
pause;
Подпрограмма fun.m
В этой подпрограмме задается матрица a
.
Текст программы:
function a=fun
%Изменяемая пользователем часть
a=[1.2551.340-1.316 0;
1.3402.526 00.516;
-1.316 0-1.7434.628;
0 0.516 4.628 0.552];
В данной работе спроектирована программа, реализующая метод скалярного произведения для нахождения максимального собственного числа матрицы. Для проверки предлагается нахождение собственных чисел (векторов) симметричной матрицы. При этом исследуется влияние вектора начального приближения к решению и значения допустимой ошибки на время вычислений и число итераций.
Найдем собственные значения исходной матрицы, используя функцию eig.
Получим
L1= -5.5251
0.2841
3.4399
4.3911
Решение исходной задачи
Исходные данные:
yn=[1,1,1,1];
ed=0.00001;
a=[1.255 1.340 -1.316 0;
1.340 2.526 0 0.516;
-1.316 0 -1.743 4.628;
0 0.516 4.628 0.552];
Данные, полученные при выполнении программы:
y = -0.1501 m = 34 L1 = -5.5251 t = 0
-0.0135
-0.7853
0.6005
График значений собственного числа заданной матрицы за время итерационного процесса

График значений собственного вектора, соответствующего собственному числу

Изменение максимальной допустимой ошибки
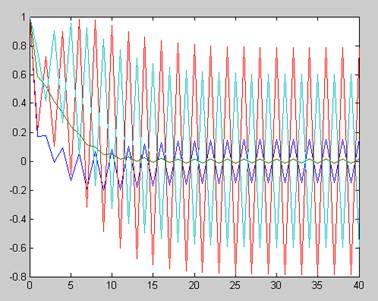
Увеличим значение допустимой ошибки
Исходные данные:
yn=[1,1,1,1];
ed=0.0001;
a=[1.255 1.340 -1.316 0;
1.340 2.526 0 0.516;
-1.316 0 -1.743 4.628;
0 0.516 4.628 0.552];
Данные, полученные при выполнении программы:
y = 0.1491 m = 29 L1 = -5.5253 t = 0
0.0136
0.7880
-0.5972
График значений собственного числа заданной матрицы за время итерационного процесса/

График значений собственного вектора, соответствующего собственному числу
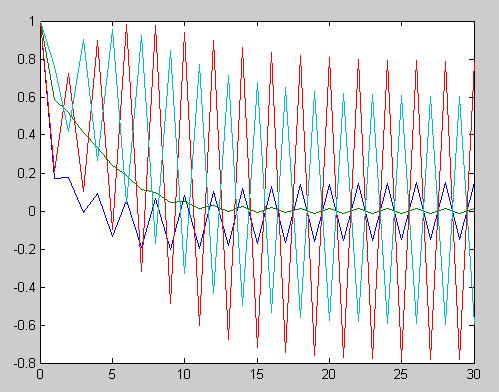
Уменьшим значение допустимой ошибки
Исходные данные:
yn=[1,1,1,1];
ed=0.000001;
a=[1.255 1.340 -1.316 0;
1.340 2.526 0 0.516;
-1.316 0 -1.743 4.628;
0 0.516 4.628 0.552];
Данные, полученные при выполнении программы:
y = 0.1498 m = 39 L1 = -5.5251 t = 0
0.0135
0.7862
-0.5994
График значений собственного числа заданной матрицы за время итерационного процесса

График значений собственного вектора, соответствующего собственному числу
Увеличимзначение начального приближения, т.е. отдалим от конечного решения.
Исходные данные:
yn=[2,3,3,2];
ed=0.00001;
a=[1.255 1.340 -1.316 0;
1.340 2.526 0 0.516;
-1.316 0 -1.743 4.628;
0 0.516 4.628 0.552];
Данные, полученные при выполнении программы:
y = -0.1501 m = 32 L1 = -5.5251 t = 1
-0.0135
-0.7853
0.6004
График значений собственного числа заданной матрицы за время итерационного процесса/

График значений собственного вектора, соответствующего собственному числу

Уменьшимзначение начального приближения, т.е. приблизимот конечного решения.
Исходные данные:
yn=[1,0,1,0];
ed=0.00001;
a=[1.255 1.340 -1.316 0;
1.340 2.526 0 0.516;
-1.316 0 -1.743 4.628;
0 0.516 4.628 0.552];
Данные, полученные при выполнении программы:
y = 0.1496 m = 25 L1 = -5.5251 t = 0
0.0135
0.7866
-0.5989
График значений собственного числа заданной матрицы за время итерационного процесса/

График значений собственного вектора, соответствующего собственному числу

Рассмотрим другие примеры:
Исходные данные:
yn=[1,1,1];
L1= 0.01
edop=0.00001;
a=[1 1 1;
2 3 4;
0 4 0];
Найдем собственные значения исходной матрицы, используя функцию eig. Получим
L1= 6.2085
0.4794
-2.6879
Полученный результат:
y = 0.2565 m =13 L1 =6.2085 t =0
0.8125
0.5235
График значений собственного числа заданной матрицы за время итерационного процесса

График значений собственного вектора, соответствующего собственному числу
Так при задании начального приближения, находящегося далеко от точного решения, итерационный процесс расходится. Если значение начального приближения выбрано близко к точному решению, то итерационный процесс сходится, и чем ближе вектор начального приближения к точному решению, тем за меньшее число итераций сходится итерационный процесс.
Выбор ошибки итерации также влияет на число итераций, а также на время счета. При уменьшении значения допустимой ошибки число итераций увеличивается, что необходимо для получения более точного значения собственного числа. И, наоборот, при увеличении значения допустимой ошибки число итераций уменьшается, а собственное число матрицы имеет более приближенное значение.
При выполнении данной работы были рассмотрены теоретически и практически основные характеристики метода скалярных произведений для нахождения максимального собственного числа симметричной матрицы и соответствующего ему вектора собственных значений. Метод отличается простотой и не требует слишком сложных вычислений, что является существенным преимуществом.
1. Сарычева О.М. Численные методы в экономике: Конспект лекций /НГТУ – Новосибирск, 1995. – 65 с.
2. Уилкинс Дж.Х. Алгебраическая проблема собственных значений. – Наука, М. 1970.
3. Фаддеев Д.К., Фаддеев В.И. Вычислительные методы линейной алгебры М. Физматиздат, 1963.
|