Завдання 1
Побудувати математичну модель задачі.
На підприємстві виготовляються вироби двох видів А і В. Для цього використовується сировина чотирьох типів – І, ІІ, ІІІ, ІV, запаси якої дорівнюють, відповідно, 21; 4; 6; 10 од. Для виготовлення одного виробу А необхідна така кількість одиниць сировини чотирьох видів: 2; 1; 0; 2. Для виробу В – 3; 0; 1; 1 од. відповідно. Випуск одного виробу А дає 3 грн. од. прибутку, типу В – 2 грн. од. Скласти план виробництва, який забезпечує найбільший прибуток.
| Сировина |
Норма витрат сировини, од |
Запаси сировини, од. |
| А |
В |
| І |
2 |
3 |
21 |
| ІІ |
1 |
0 |
4 |
| ІІІ |
0 |
1 |
6 |
| ІV |
2 |
1 |
10 |
| Ціна, грн. од. |
3 |
2 |
Розв’язок
Складаємо математичну модель задачі. Позначимо через х
1
кількість виробів 1-ї моделі, що виготовляє підприємство за деяким планом, а через х2
кількість виробів 2-ї моделі.Тоді прибуток, отриманий підприємством від реалізації цих виробів, складає
∫ = 3х1
+2х2
.
Витрати сировини на виготовлення такої кількості виробів складають відповідно:
CI
=2х1
+ 3х2
,
CII
=1х1
+ 0х2
,
CIII
=0х1
+ 1х2
,
CIV
=2х1
+ 1х2
,
Оскільки запаси сировини обмежені, то повинні виконуватись нерівності:
2х1
+ 3х2
≤ 21
1х1
≤ 4
1х2
≤ 6
2х1
+ 1х2
≤ 10
Оскільки, кількість виробів є величина невід'ємна, то додатково повинні виконуватись ще нерівності: х1
> 0, х2
>0.
Таким чином, приходимо до математичної моделі (задачі лінійного програмування):
Знайти х1
, х2
такі, що функція ∫ = 3х1
+2х2
досягає максимуму при системі обмежень:
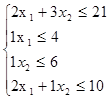
Розв'язуємо задачу лінійного програмування симплексним методом.
Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних. Оскільки маємо змішані умови-обмеження, то введемо штучні змінні x.
2x1
+ 3x2
+ 1x3
+ 0x4
+ 0x5
+ 0x6
= 21
1x1
+ 0x2
+ 0x3
+ 0x4
+ 0x5
+ 1x6
= 4
0x1
+ 1x2
+ 0x3
+ 1x4
+ 0x5
+ 0x6
= 6
2x1
+ 1x2
+ 0x3
+ 0x4
+ 1x5
+ 0x6
= 10
де х1
,...,х6
>0
Для постановки задачі на максимум цільову функцію запишемо так:
F(X) = 3 x1
+2 x2
- M x6
=>max
Оскільки завдання вирішується на максимум, то ведучий стовпець вибираємо по максимальному негативному кількістю та індексного рядку. Всі перетворення проводять до тих пір, поки не вийдуть в індексному рядку позитивні елементи.
Складаємо симплекс-таблицю:
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
min |
| 1 |
x3
|
21 |
2 |
3 |
1 |
0 |
0 |
0 |
10.5 |
| x6
|
4 |
1
|
0 |
0 |
0 |
0 |
1 |
4
|
| x4
|
6 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
| x5
|
10 |
2 |
1 |
0 |
0 |
1 |
0 |
5 |
| Індексний рядок |
F(X1) |
-400000 |
-100003
|
-2 |
0 |
0 |
0 |
0 |
0 |
Оскільки, в індексному рядку знаходяться негативні коефіцієнти, поточний опорний план неоптимальний, тому будуємо новий план. У якості ведучого виберемо елемент у стовбці х1
, оскільки значення коефіцієнта за модулем найбільше.
математична модель симплекс транспортна задача екстремум
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
min |
| 2 |
x3
|
13 |
0 |
3 |
1 |
0 |
0 |
-2 |
4.33 |
| x1
|
4 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| x4
|
6 |
0 |
1 |
0 |
1 |
0 |
0 |
6 |
| x5
|
2 |
0 |
1
|
0 |
0 |
1 |
-2 |
2
|
| Індексний рядок |
F(X2) |
12 |
0 |
-2
|
0 |
0 |
0 |
100003 |
0 |
Даний план, також не оптимальний, тому будуємо знову нову симплексну таблицю. У якості ведучого виберемо елемент у стовбці х2
.
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
Min |
| 3 |
x3
|
7 |
0 |
0 |
1 |
0 |
-3 |
4 |
4.33 |
| x1
|
4 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| x4
|
4 |
0 |
0 |
0 |
1 |
-1 |
2 |
6 |
| x2
|
2 |
0 |
1 |
0 |
0 |
1 |
-2 |
2 |
| Індексний рядок |
F(X3) |
16 |
0 |
0 |
0 |
0 |
2 |
99999 |
0 |
Оскільки всі оцінки >0,
то знайдено оптимальний план, що забезпечує максимальний прибуток: х1
=4, х2
=2. Прибуток, при випуску продукції за цим планом, становить 16 грн.
Завдання 2
Записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну із задач симплексним методом і визначити оптимальний план іншої задачі. Оптимальні результати перевірити графічно.

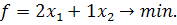
Розв’язок
Пряма задача лінійного програмування має вигляд:
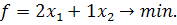
При обмеженнях:

Оскільки, у прямій задачі лінійного програмування необхідно знайти мінімум функції, то приведемо першопочаткову умову до вигляду:

Для досягнення відповідного вигляду помножимо 1-у та 2-у нерівність на -1
1х1
-4ч2
≥-8
-1х1
+1х2
≥-3
В результаті отримаємо наступні матриці:
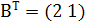


Для складання двоїстої задачі лінійного програмування знайдемо матриці А, В, СТ
.


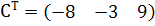
Відповідно, двоїста задача лінійного програмування матиме вигляд:
F(Y)= -8Y1
-3Y2
+9Y3
(max)
Обмеження:
1Y1
-1Y2
+2Y3
≤2
-4Y1
+1Y2
+1Y3
≤1
Y1
≥0
Y2
≥0
Y3
≥0
Розв’яжемо задачу лінійного програмування симплексним методом.
Визначимо мінімальне значення цільової функції F(X) = 2x1
+x2
при наступних умовах-обмежень.
-x1
+4x2
≤8
x1
-x2
≤3
2x1
+x2
≥9
Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних.
Оскільки маємо змішані умови-обмеження, то введемо штучні змінні x.
-1x1
+ 4x2
+ 1x3
+ 0x4
+ 0x5
+ 0x6
= 8
1x1
-1x2
+ 0x3
+ 1x4
+ 0x5
+ 0x6
= 3
2x1
+ 1x2
+ 0x3
+ 0x4
-1x5
+ 1x6
= 9
Для постановки задачі на мінімум цільову функцію запишемо так:
F(X) = 2 x1
+ x2
+M x6
=>min
Переходимо до основного алгоритму симплекс-методу.
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
Min |
| 1 |
x3
|
8 |
-1 |
4 |
1 |
0 |
0 |
0 |
0 |
| x4
|
3 |
1
|
-1 |
0 |
1 |
0 |
0 |
3
|
| x6
|
9 |
2 |
1 |
0 |
0 |
-1 |
1 |
4.5 |
| Індексний рядок |
F(X1) |
900000 |
199998
|
99999 |
0 |
0 |
-100000 |
0 |
0 |
Оскільки, в індексному рядку знаходяться позитивні коефіцієнти, поточний опорний план неоптимальний, тому будуємо новий план. У якості ведучого виберемо елемент у стовбці х1
, оскільки значення коефіцієнта за модулем найбільше.
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
min |
| 2 |
x3
|
11 |
0 |
3 |
1 |
1 |
0 |
0 |
3.67 |
| x1
|
3 |
1 |
-1 |
0 |
1 |
0 |
0 |
0 |
| x6
|
3 |
0 |
3
|
0 |
-2 |
-1 |
1 |
1
|
| Індексний рядок |
F(X2) |
300006 |
0 |
299997
|
0 |
-199998 |
-100000 |
0 |
0 |
Даний план, також не оптимальний, тому будуємо знову нову симплексну таблицю. У якості ведучого виберемо елемент у стовбці х2
.
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
min |
| 3 |
x3
|
8 |
0 |
0 |
1 |
3 |
1 |
-1 |
3.67 |
| x1
|
4 |
1 |
0 |
0 |
0.33 |
-0.33 |
0.33 |
0 |
| x2
|
1 |
0 |
1 |
0 |
-0.67 |
-0.33 |
0.33 |
1 |
| Індексний рядок |
F(X3) |
9 |
0 |
0 |
0 |
0 |
-1 |
-99999 |
0 |
Остаточнийваріант симплекс-таблиці оптимальний, тому що в індексному рядку знаходяться негативні коефіцієнти.
Оптимальний план можна записати так:
x3
= 8
x1
= 4
x2
= 1
F(X) = 2*4 + 1*1 = 9
Визначаємо оптимальний план двоїстої задачі до поставленої задачі лінійного програмування.
F(Y)= -8Y1
-3Y2
+9Y3
(max)
Обмеження:
1Y1
-1Y2
+2Y3
≤2
-4Y1
+1Y2
+1Y3
≤1
Y1
≥0
Y2
≥0
Y3
≥0
Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних.
1x1
-1x2
+ 2x3
+ 1x4
+ 0x5
= 2
-4x1
+ 1x2
+ 1x3
+ 0x4
+ 1x5
= 1
Вважаючи, що вільні змінні рівні 0, отримаємо перший опорний план:
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
| 0 |
x4
|
2 |
1 |
-1 |
2 |
1 |
0 |
| x5
|
1 |
-4 |
1 |
1 |
0 |
1 |
| Індексний рядок |
F(X0) |
0 |
8 |
3 |
-9 |
0 |
0 |
Перейдемо до основного алгоритму симплекс-метода.Оскільки в останньому стовбці присутньо кілька мінімальних елементів 1, то номер рядка вибираємо по правилу Креко
.
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
min |
| 1 |
x4
|
2 |
1 |
-1 |
2
|
1 |
0 |
1
|
| x5
|
1 |
-4 |
1 |
1 |
0 |
1 |
1 |
| Індексний рядок |
F(X1) |
0 |
8 |
3 |
-9
|
0 |
0 |
0 |
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
min |
| 2 |
x3
|
1 |
0.5 |
-0.5 |
1 |
0.5 |
0 |
0 |
| x5
|
0 |
-4.5 |
1.5
|
0 |
-0.5 |
1 |
0
|
| Индекснаястрока |
F(X2) |
9 |
12.5 |
-1.5
|
0 |
4.5 |
0 |
0 |
| План |
Базис |
В |
x1
|
x2
|
x3
|
x4
|
x5
|
| 3 |
x3
|
1 |
-1 |
0 |
1 |
0.3333 |
0.3333 |
| x2
|
0 |
-3 |
1 |
0 |
-0.3333 |
0.6667 |
| Индекснаястрока |
F(X3) |
9 |
8 |
0 |
0 |
4 |
1 |
Оптимальний план можливо записати так:
x3
= 1
x2
= 0
F(X) = -3*0 + 9*1 = 9
Завдання 3
Розв’язати транспортну задачу.
| 5 |
1 |
2 |
3 |
4 |
150 |
| 7 |
8 |
1 |
1 |
2 |
320 |
| 4 |
1 |
3 |
1 |
2 |
400 |
| 100 |
120 |
100 |
200 |
300 |
Розв’язок
Побудова математичної моделі
. Нехай xij
— кількість продукції, що перевозиться з і
-го пункту виробництва до j
-го споживача 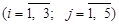 . Оскільки . Оскільки  , то задачу треба закрити, тобто збалансувати (зрівняти) поставки й потреби: , то задачу треба закрити, тобто збалансувати (зрівняти) поставки й потреби:
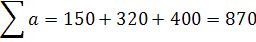

 У нашому випадку робиться це введенням фіктивного постачальника, оскільки У нашому випадку робиться це введенням фіктивного постачальника, оскільки  . З уведенням фіктивного споживача в транспортній таблиці додатково заявляється n робочих клітинок (додатковий стовпчик). . З уведенням фіктивного споживача в транспортній таблиці додатково заявляється n робочих клітинок (додатковий стовпчик).
Виникає проблема, які ціни присвоїти цим клітинкам, щоб фіктивний стовпчик був нейтральним щодо оптимального вибору планових перевезень. Нейтральність забезпечується тим, що всі ціни у фіктивних клітинках вибираються однаковими, а оскільки ці ціни при поставках не повинні впливати на значення цільової функції f, то їх беруть усі рівними нулю.
Занесемовихіднідані у таблицю.
| В1
|
В2
|
В3
|
В4
|
В5
|
В6
|
Запаси |
| А1
|
5 |
1 |
2 |
3 |
4 |
0 |
150 |
| А2
|
7 |
8 |
1 |
1 |
2 |
0 |
320 |
| А3
|
4 |
1 |
3 |
1 |
2 |
0 |
400 |
| Потреби |
100 |
120 |
100 |
200 |
300 |
50 |
Забезпечивши закритість розв'язуваної задачі, розпочинаємо будувати математичну модель даної задачі:
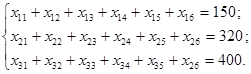
Економічний зміст записаних обмежень полягає в тому, що весь вантаж потрібно перевезти по пунктах повністю.
Аналогічні обмеження можна записати відносно замовників: вантаж, що може надходити до споживача від чотирьох баз, має повністю задовольняти його попит. Математично це записується так:

Загальні витрати, пов’язані з транспортуванням продукції, визначаються як сума добутків обсягів перевезеної продукції на вартості транспортування од. продукції до відповідного замовника і за умовою задачі мають бути мінімальними. Тому формально це можна записати так:
minZ
= 5x
11
+ 1x
12
+ 2x
13
+ 3x
14
+4x
15
+ 0x
16
+7x
21
+ 8x
22
+ 1x
23
+ 1x
24
+2x
25
+0x
26
+4x
31
+ 1x
32
+ 3x
33
+ 1x
34
+2x
35
+ 0x
36
.
Загалом математична модель сформульованої задачі має вигляд:
minZ
= 5x
11
+ 1x
12
+ 2x
13
+ 3x
14
+4x
15
+ 0x
16
+7x
21
+ 8x
22
+ 1x
23
+ 1x
24
+2x
25
+0x
26
+4x
31
+ 1x
32
+ 3x
33
+ 1x
34
+2x
35
+ 0x
36
.
за умов:
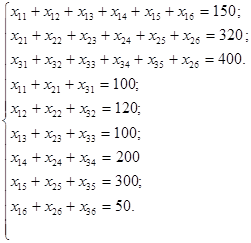
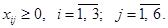
Запишемо умови задачі у вигляді транспортної таблиці та складемо її перший опорний план у цій таблиці методом «північно-західного кута».
| Ai
|
Bj
|
ui
|
| b
1
= 100 |
b
2
= 120 |
b
3
= 100 |
b
4
=200 |
b
5
=300 |
B
6
=50 |
| а
1
= 150 |
5
[-] 100
|
1
[+] 50
|
2
|
3
|
4
|
0
|
u
1
= 0 |
| а
2
= 320 |
7
|
8
[-] 70
|
1
100
|
1
[+] 150
|
2
|
0
|
u
2
= 7 |
| а
3
= 400 |
4
[+]
|
1
|
3
|
1
[-] 50
|
2
300
|
0
50
|
u
3
= 7 |
| vj
|
v
1
= 5 |
v
2
= 1 |
v
3
= -6 |
v
4
= -6 |
v
5
= -5 |
V
6
= -7 |
В результатіотримано перший опорний план, який є допустимим, оскількивсівантажі з баз вивезені, потреба магазинівзадоволена, а план відповідаєсистеміобмеженьтранспортноїзадачі.
Підрахуємо число зайнятих клітин таблиці, їх 8, а має бути m+n-1=8. Отже, опорний план є не вироджених.
Перевіримооптимальність опорного плану.Знайдемо потенціали ui
, vi
. по зайнятих клітинам таблиці, в яких ui
+ vi
= cij
, вважаючи, що u1
= 0.
Тоді всі інші потенціали однозначно визначаються з цієї системи рівнянь: u
1
=0, u
2
= 7, u
3
= 7, v
1
=5, v
2
=1, v
3
= -6 v
4
=1, v
5
= -5, v
6
= -7. Ці значення потенціалів першого опорного плану записуємо у транспортну таблицю.
Потім згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності ui
+ vj
≤ cij
(для порожніх клітинок таблиці):
Опорний план не є оптимальним, тому щоіснуютьоцінкивільнихклітин для якихui
+ vi
>cij
(2;1): 7 + 5 > 7
(3;1): 7 + 5 > 4
(3;2): 7 + 1 > 1
Тому відньогонеобхідно перейти до другого плану, змінившиспіввідношеннязаповнених і порожніхклітиноктаблиці. Вибираємомаксимальнуоцінкувільноїклітини (А
3
B
1
): 4
Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки А
3
B
1
, та позначаємо вершини циклу почергово знаками «–» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у порожню клітинку А
3
B
1
переносимо менше з чисел хij
, які розміщені в клітинках зі знаком «–». Одночасно це саме число хij
додаємо до відповідних чисел, що розміщені в клітинках зі знаком «+», та віднімаємо від чисел, що розміщені в клітинках, позначених знаком «–».
З вантажів хij
що стоять в мінусових клітинах, вибираємо найменше,  , тобто , тобто 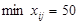 . Додаємо 50 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 50 з Хij
, що стоять в мінусових клітинах. В результатіотримаємоновийопорний план. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписуємо у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості плану, тобто дорівнювати (n
+ m
– 1). . Додаємо 50 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 50 з Хij
, що стоять в мінусових клітинах. В результатіотримаємоновийопорний план. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписуємо у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості плану, тобто дорівнювати (n
+ m
– 1).
Отже, другий опорний план транспортної задачі матиме такий вигляд:
| Ai
|
Bj
|
ui
|
| b
1
= 100 |
b
2
= 120 |
b
3
= 100 |
b
4
=200 |
b
5
=300 |
B
6
=50 |
| а
1
= 150 |
5
[-] 50
|
1
[+] 100
|
2
|
3
|
4
|
0
|
u
1
= 0 |
| а
2
= 320 |
7
|
8
[-] 20
|
1
100
|
1
200
|
2
[+]
|
0
|
u
2
= 7 |
| а
3
= 400 |
4
[+] 50
|
1
|
3
|
1
|
2
[-] 300
|
0
50
|
u
3
= -1 |
| vj
|
v
1
= 5 |
v
2
= 1 |
v
3
= -6 |
v
4
= -6 |
v
5
= 3 |
V
6
= 1 |
Перевіримооптимальністьопорного плану. Знайдемопотенціалиui
, vi
. по зайнятихклітинамтаблиці, в якихui
+ vi
= cij
, вважаючи, щоu1
= 0.
Опорний план не є оптимальним, тому щоіснуютьоцінкивільнихклітин для якихui
+ vi
>cij
(1;6): 0 + 1 > 0
(2;1): 7 + 5 > 7
(2;5): 7 + 3 > 2
(2;6): 7 + 1 > 0
Вибираємомаксимальнуоцінкувільноїклітини (А
2
B
5
): 2
Для цього в перспективнуклітку (А
2
B
5
) поставимо знак «+», а в інших вершинах багатокутникачергуються знаки «-», «+», «-». Цикл наведено втаблиці.
Звантажів хij
що стоять в мінусовихклітинах, вибираємонайменше, тобто у = min (А
2
B
2
) = 20. Додаємо 20 до обсягіввантажів, що стоять в плюсовихклітинах і віднімаємо 20 з Хij
, що стоять в мінусовихклітинах. В результатіотримаємоновийопорний план.
| Ai
|
Bj
|
ui
|
| b
1
= 100 |
b
2
= 120 |
b
3
= 100 |
b
4
=200 |
b
5
=300 |
B
6
=50 |
| а
1
= 150 |
5
[-] 30
|
1
120
|
2
|
3
|
4
|
0
[+]
|
u
1
= 0 |
| а
2
= 320 |
7
|
8
|
1
100
|
1
200
|
2
20
|
0
|
u
2
= -1 |
| а
3
= 400 |
4
[+] 70
|
1
|
3
|
1
|
2
280
|
0
[-] 50
|
u
3
= -1 |
| vj
|
v
1
= 5 |
v
2
= 1 |
v
3
= 2 |
v
4
= 2 |
v
5
= 3 |
V
6
= 1 |
Перевіримо оптимальність опорного плану, тобто повторюємо описані раніше дії.
Знайдемо потенціали ui
, vi
. по зайнятих клітинам таблиці, в яких ui
+ vi
= cij
, вважаючи, що u1
= 0.
Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він неоптимальний. Тому знову будуємо новий опорний план.
| Ai
|
Bj
|
ui
|
| b
1
= 100 |
b
2
= 120 |
b
3
= 100 |
b
4
=200 |
b
5
=300 |
B
6
=50 |
| а
1
= 150 |
5
|
1
120
|
2
|
3
|
4
|
0
30
|
u
1
= 0 |
| а
2
= 320 |
7
|
8
|
1
100
|
1
200
|
2
20
|
0
|
u
2
= 0 |
| а
3
= 400 |
4
100
|
1
|
3
|
1
|
2
280
|
0
20
|
u
3
= 0 |
| vj
|
v
1
= 4 |
v
2
= 1 |
v
3
= 1 |
v
4
= 1 |
v
5
= 2 |
V
6
= 0 |
Перевіримооптимальність опорного плану, тобто повторюємо описані раніше дії.
Знайдемо потенціали ui
, vi
. по зайнятих клітинам таблиці, в яких ui
+ vi
= cij
, вважаючи, що u1
= 0.
Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний.
Розрахуємозначенняцільовоїфункціївідповідно до другого опорного плану задачі:
(x) = 1*120 + 0*30 + 1*100 + 1*200 + 2*20 + 4*100 + 2*280 + 0*20 = 1420
За оптимальним планом перевезень загальна вартість перевезень всієї продукції є найменшою і становить 540 грн.
Завдання 4
Знайти графічним методом екстремуми функції в області, визначеній нерівностями (в усіх варіантах вважати  ) )
 , ,  , , 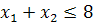 , , 
Розв’язок
Побудуємо область допустимих рішень, тобто вирішимо графічно систему нерівностей. Для цього побудуємо кожну пряму і визначимо півплощини, задані нерівностями (півплощини позначені штрихом).

Межі області
Позначимо границі області багатокутника рішень.
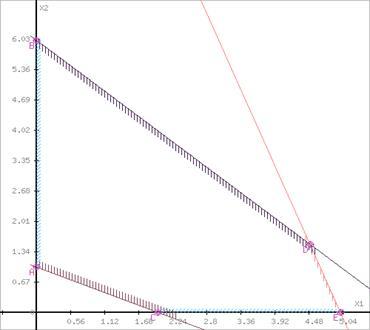
Цільова функція F(x) =>min
Розглянемо цільову функцію завдання F = 7X1+9X2 =>min.
Побудуємо пряму, що відповідає значенню функції F = 0: F = 7X1+9X2 = 0. Будемо рухати цю пряму паралельним чином. Оскільки нас цікавить мінімальне рішення, тому рухався прямо до першого торкання позначеної області. На графіку ця пряма позначена пунктирною лінією.
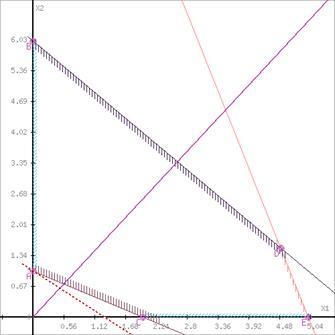
Рівний масштаб

Перетином півплощини буде область, яка представляє собою багатокутник, координати точок якого задовольняють умові нерівностей системи обмежень задачі.Пряма F(x) = const перетинає область у точці A. Оскільки точка A отримана в результаті перетину прямих 2 i 5, то її координати задовольняють рівнянням цих прямих:
x1+2x2≥2
x1=0
Вирішивши систему рівнянь, одержимо: x1 = 0, x2 = 1
Звідки знайдемо мінімальне значення цільової функції:
F(X) = 7*0 + 9*1 = 9
|