МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Національний університет “Львівська політехніка”
Інститут Комп’ютерних наук та інформаційних технологій
Кафедра автоматизованих систем управління
Лабораторна робота № 5-6
з дисципліни
“Математичні методи представлення знань”
на тему:
«Обчислення означених інтегралів»
Виконав:
студент групи КН-29
Коцуба О.
Прийняв:
Биненко Б. І.
Львів – 2011
Обчислення означених інтегралів
Мета роботи: вивчити методи наближених обчислень і запрограмувати алгоритми обчислення означених інтегралів .
Порядок роботи:
1. Попереднє опрацювання теоретичного матеріалу.
2. Отримання допуску до виконання лабораторної роботи.
3. Опрацювання типового навчального завдання (прикладів).
4. Створення проекту для виконання індивідуального завдання.
5. Оформити звіт для захисту лабораторної роботи за зразком:
· назва роботи;
· мета роботи;
· порядок роботи;
· короткі теоретичні відомості;
· алгоритм розв’язування задачі;
· тексти відповідних модулів проекту;
· аналіз отриманих результатів та висновки.
6. Захист лабораторної роботи.
Короткі теоретичні відомості
1. Формули прямокутників.
Нехай на відрізку задана неперервна функція задана неперервна функція  . Потрібно обчислити інтеграл . Потрібно обчислити інтеграл 
Розіб’ємо відрізок  на n рівних частин точками на n рівних частин точками  , i=0,1,…n-1, довжина кожної з яких дорівнює , i=0,1,…n-1, довжина кожної з яких дорівнює  . Через . Через  позначимо значення функції позначимо значення функції  в точках в точках  і складемо суми і складемо суми
 або або  
Кожна з цих сум є інтегральною сумою для  на відрізку на відрізку і тому наближено виражають означений інтеграл: і тому наближено виражають означений інтеграл:
 (1) (1)
 (1/) (1/)
Ці формули називаються формулами прямокутників. Із рис. 1 видно, що якщо  додатна і зростаюча функція, то формула (1) відображає площу ступінчатої фігури, що складена із “ внутрішніх” прямокутників, а формула (1/) – площу фігури, що складена із “зовнішніх” прямокутників. додатна і зростаюча функція, то формула (1) відображає площу ступінчатої фігури, що складена із “ внутрішніх” прямокутників, а формула (1/) – площу фігури, що складена із “зовнішніх” прямокутників.
Похибка методу прямокутників дається формулою (2):
 (2) (2)
формула прямокутник лагранж функція
Похибка при цьому буде тим меншою, чим більше число n (тобто чим менший крок поділу ). Зауважимо, що формули прямокутників дають точні результати для багаточленів першого степеня. ). Зауважимо, що формули прямокутників дають точні результати для багаточленів першого степеня.
2. Формула трапецій.
Очевидно, що можна отримати більш точне значення інтеграла, якщо дану криву  замінити не ступінчатою лінією, як це мало місце у формулі прямокутників, а вписаною ламаною (рис.2). Тоді площа криволінійної трапеції, обмеженої лініями замінити не ступінчатою лінією, як це мало місце у формулі прямокутників, а вписаною ламаною (рис.2). Тоді площа криволінійної трапеції, обмеженої лініями  і заміниться площами трапецій, обмежених зверху хордами Оскільки площа і заміниться площами трапецій, обмежених зверху хордами Оскільки площа

Рис.1 Рис.2
першої трапеції дорівнює  другої – другої –  і т.д., і т.д.,
то 
або
 (3) (3)
Формула (3) називається формулою трапецій. Число n вибирається довільним, але чим більшим це число буде, а значить, крок  меншим, тим з більшою точністю сума в правій частині наближеної рівності (3) буде давати значення інтегралу. меншим, тим з більшою точністю сума в правій частині наближеної рівності (3) буде давати значення інтегралу.
3. Формула парабол (Сімпсона).
Метод Сімпсона найпоширеніший і простіше застосовний для програмування. Його суть полягає в наближенні підінтегральної функції відрізками парабол.
Отже, розглянемо спочатку інтеграл  , де , де 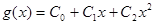 – парабола; – парабола; 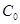 , ,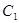 , ,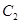 – деякі параметри (або числа). – деякі параметри (або числа).
Тоді


Нехай тепер маємо інтеграл 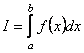 , де , де 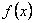 - неперервна на інтервалі - неперервна на інтервалі функція. Якщо інтервал розбити на п рівних частинок функція. Якщо інтервал розбити на п рівних частинок  , i=0,1,…n-1,, то заданий інтеграл І можна записати так: , i=0,1,…n-1,, то заданий інтеграл І можна записати так:
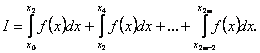
Якщо на кожному з інтегралів для проміжків 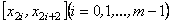 функцію функцію 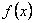 замінимо параболами замінимо параболами 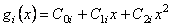 , що проходять через точки , що проходять через точки 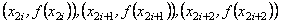 ,то одержимо ,то одержимо
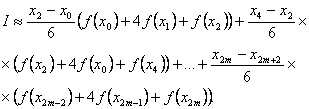
Через те, що, формула матиме вигляд:
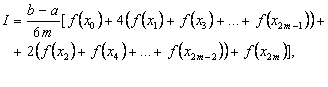 або або

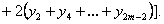 (4) (4)
Формула (4) називається формулою парабол або Сімпсона. Доведено, що похибка обчислень  за формулою Сімпсона є такою: за формулою Сімпсона є такою:
 (5) (5)
Проте, цією оцінкою похибки можна користуватись, якщо 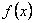 є хоча б чотири рази диференційовною. Але, якщо є хоча б чотири рази диференційовною. Але, якщо 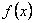 навіть чотири рази диференційовна, то часто оцінка четвертої похідної навіть чотири рази диференційовна, то часто оцінка четвертої похідної 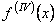 може виявитись досить складною. Тому на практиці переважно користуються таким методом: обчислюють інтеграл, розділяючи інтервал, заданий границями інтегрування, один раз на n рівних частин, а другий раз на т частин. Якщо одержані двоє значень інтеграла мало відрізняються, то результат можна вважати прийнятним. Порівнюючи їх можна оцінити і точність обчислень. може виявитись досить складною. Тому на практиці переважно користуються таким методом: обчислюють інтеграл, розділяючи інтервал, заданий границями інтегрування, один раз на n рівних частин, а другий раз на т частин. Якщо одержані двоє значень інтеграла мало відрізняються, то результат можна вважати прийнятним. Порівнюючи їх можна оцінити і точність обчислень.
Приклад. Обчислити з точністю до 0,001 інтеграл

Р о з в ’ я з у в а н н я. За формулою (4) маємо:
при при
 |
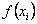 |
 |
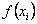 |
 |
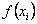 |
 |
-0,5 |
0,0000 |
 |
-0,5 |
0,00000 |
 |
0,05 |
0,0371 |
 |
-0,4 |
-0,1203 |
 |
-0,45 |
-0,0946 |
 |
0,10 |
0,0772 |
 |
-0,3 |
-0,1303 |
 |
-0,40 |
-0,1203 |
 |
0,15 |
0,1200 |
 |
-0,2 |
-0,1081 |
 |
-0,35 |
-0,1304 |
 |
0,20 |
0,1652 |
 |
-0,1 |
-0,630 |
 |
-0,30 |
-0,1303 |
 |
0,25 |
0,2122 |
 |
0 |
0,0000 |
 |
-0,25 |
-0,1204 |
 |
0,30 |
0,2607 |
 |
0,1 |
0,0772 |
 |
-0,20 |
-0,1081 |
 |
0,35 |
0,3103 |
 |
0,2 |
0,1652 |
 |
-0,15 |
-0,0881 |
 |
0,40 |
0,3610 |
 |
0,3 |
0,2607 |
 |
-0,10 |
-0,0630 |
 |
0,45 |
0,4121 |
 |
0,4 |
0,36098 |
 |
-0,05 |
-0,0335 |
 |
0,50 |
0,4637 |
 |
0,5 |
0,46365 |
 |
0,00 |
0,0000 |
Отже,
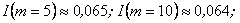 . .
Нехай деяка функціяf(x) задана в вузлах інтерполяції:
(i=1,2,3.,n) на відрізку [а,b] таблицею значень: 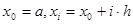 . .
Потрібно знайти значення інтегралу  . .
Спершу складемо інтерполяційний багаточлен Лагранжа:
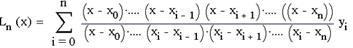
Для рівновіддалених вузлів інтерполяційний багаточлен має вигляд:
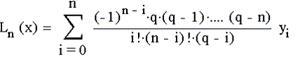
де q=(x-x0) /h – крок інтерполяції, замінимо підінтегральну функцію f(x) інтерполяційним багаточленом Лагранжа:
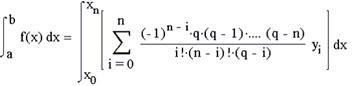
Поміняємо знак підсумовування і інтеграл і винесемо за знак інтеграла постійні елементи:
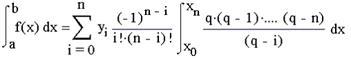
Оскільки dp=dx/h, то, замінивши межі інтеграції, маємо:

Для рівновіддалених вузлів інтерполяції на відрізку [а,b] величина крок визначається як h=(b-a)/n. Представивши цей вираз для h у формулу (4) і виносячи (b-a) за знак суми, отримаємо:
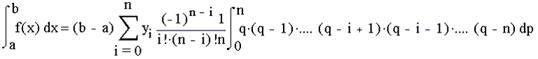
Покладемо, що

де i=0,1,2.,n; Числа  називають коефіцієнтами Ньютона-Kотеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки по n. Тому їх можна обчислити заздалегідь. Остаточна формула виглядає так: називають коефіцієнтами Ньютона-Kотеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки по n. Тому їх можна обчислити заздалегідь. Остаточна формула виглядає так:

Формула трьох восьмих:
Якщо в формулі Ньютона-Котеса взяти n = 3, тобто функцію f(x) замінити інтерполяційним багаточленом третього степеня, побудованим за значення функції f(x) у точках x0=a, x1=a+h, x2=a+2h, x3=b, h=(b-a )/3. то одержимо таку квадратурну формулу:
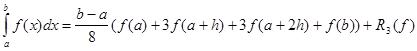 де де
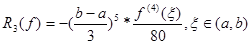
Ця квадратурна формула називається малою квадратурною формулою трьох восьмих. Використовуючи цю формулу, легко записати велику квадратурну формулу трьох восьмих.
Завдання
Обчислити інтеграл методом прямокутників, трапецій, парабол, трьох восьмих, Монте-Карло оцінити абсолютну та відносну похибку обчислення :
А) заданий інтеграл обчислити наближено та точно.
B) заданий інтеграл обчислити наближено.
Варіант 1
1. 
2. 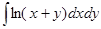
3. 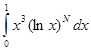
Варіант 2
1. 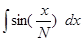
2. 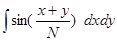
3. 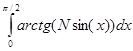
Варіант 3
1. 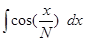
2. 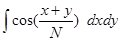
3. 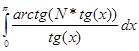
Варіант 4
1. 
2. 
3. 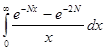
Варіант 5
1. 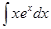
2. 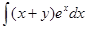
3. 
Варіант 6
1. 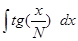
2. 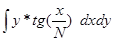
3. 
Варіант 7
1. 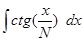
2. 
3. 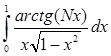
Варіант 8
1. 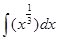
2. 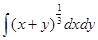
3. 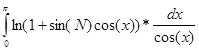
Варіант 9
1. 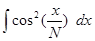
2. 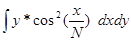
3. 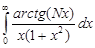
Варіант 10
1. 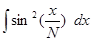
2. 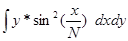
3. 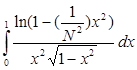
Рекомендована література:
1. Цегелик Г.Г. Чисельні методи: Підручник. – Львів: Видавничий центр ЛНУ ім. І. Франка, 2004. – 408 с.
2. Коссак О., Тумашова О., Коссак О. Методи наближених обчислень: Навч. посіб. – Львів: Бак, 2003. – 168 с.
3. Анджейчак І.А., Федю Є.М., Анохін В.Є. і ін. Практикум з обчислювальної математики. Основні числові методи. Частина І. – Навч. посіб. Львів: Вид-во ДУ «Львівська політехніка», 2000. – 100 с.
4. Дудикевич А.Т., Левицька С.М., Шахно С.М. Практична реалізація методів розв’язування нелінійних рівнянь і систем: Навч.-метод. посібн. – Львів: ВЦ ЛНУ ім.. І.Франка, 2007. – 78 с.
5. Паранчук Я.С. та ін. Алгоритмізація, програмування, числові та символьні обчислення в пакеті MathCAD. – Навч. посіб. / Я.С. Паранчук, А.В. Маляр, Р.Я. Паранчук, І.Р. Головач. – Львів: Вид-во Львівської політехніки, 2008. – 164 с.
|