Министерство высшего и профессионального образования РФ
Ижевский государственный технический университет
Воткинский филиал
Кафедра «Техническая механика»
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту по курсу «Детали машин»
Вариант Т-7-5: «Механизм привода поворотной части робота»
Выполнил: студент Бегеев А. М.
группа Т–712
Руководитель проекта: Юрченко С. А.
2002
Содержание
ВВЕДЕНИЕ
1 ИСХОДНЫЕ ДАННЫЕ
2 КИНЕМАТИЧЕСКИЕ РАСЧЕТЫ
2.1 Выбор электродвигателя
2.2 Определение передаточных чисел привода
2.3 Определение вращающих моментов на валах привода
3 РАСЧЕТ ЗУБЧАТЫХ ПЕРЕДАЧ
3.1 Выбор твердости, термической обработки и материала колес
3.2 Допускаемые напряжения
3.3 Расчет межосевого расстояния
3.4 Предварительные основные размеры колес
3.5 Диаметры валов
3.6 Модуль передач
3.7 Суммарное число зубьев и угол наклона
3.8 Число зубьев шестерни и колеса
3.9 Фактическое передаточное число
3.10 Диаметры колес
3.11 Размеры заготовок колес
3.12 Силы в зацеплении
3.13 Проверка зубьев колес по напряжениям изгиба
3.14 Проверка зубьев колес по контактным напряжениям
4 РАСЧЕТ ЭЛЕМЕНТОВ КОРПУСА РЕДУКТОРА
5 ПОДБОР ПОДШИПНИКОВ ПО ДИНАМИЧЕСКОЙ ГРУЗОПОДЪЁМНОСТИ
5.1 Определение радиальных реакций
5.2 Определение осевых нагрузок
6 ПРОВЕРОЧНЫЙ РАСЧЕТ ВАЛОВ
7 ПРОВЕРКА ПРОЧНОСТИ ШПОНОЧНОГО СОЕДИНЕНИЯ
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Технический уровень всех отраслей народного хозяйства в значительной мере определятся уровнем развития машиностроения. На основе развития машиностроения осуществляется комплексная механизация и автоматизация производственных процессов в промышленности, строительстве, сельском хозяйстве, на транспорте.
В данном проекте разрабатывается привод поворотной части робота, состоящий из поворотной колонны и редуктора.
Редуктором называют механизм, состоящий из зубчатых или червячных передач, выполненный в виде отдельного агрегата и служащий для передачи мощности от двигателя к рабочей машине. Назначение редуктора – понижение угловой скорости и повышение вращающего момента ведомого вала по сравнению с валом ведущим.

Рис. 1. Кинематическая схема привода
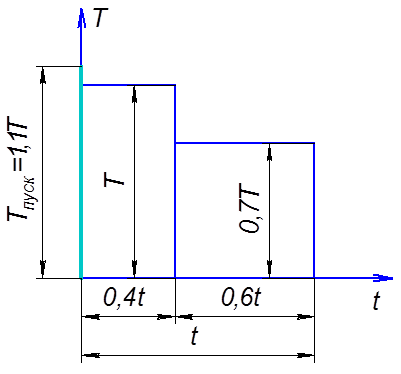
Рис. 2. График загрузки
2.1 Выбор электродвигателя
Потребную мощность электродвигателя определим по формуле:
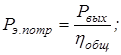
где 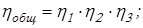
Здесь 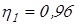 – КПД цилиндрической передачи; – КПД цилиндрической передачи;
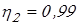 – КПД пары подшипников качения; – КПД пары подшипников качения;
 – КПД соединительной муфты. – КПД соединительной муфты.
Вычисляем общий КПД привода:
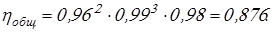
Потребная мощность электродвигателя:
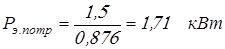 . .
Определим частоту вращения вала электродвигателя по формуле
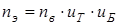 , ,
где  , ,  – передаточные числа тихоходной и быстроходной ступеней, соответственно. – передаточные числа тихоходной и быстроходной ступеней, соответственно.
Рекомендуемые значения передаточных чисел 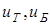 принимаем по таблице 1.2 [1], получаем: принимаем по таблице 1.2 [1], получаем:
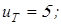
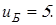
Вычисляем частоту вращения электродвигателя:

По справочнику [2] подбираем электродвигатель 4А112МА8 со следующими характеристиками:
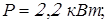
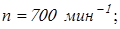
Определим окончательное общее передаточное число привода по формуле:
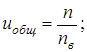
получим

Полученное расчетом общее передаточное число распределим между ступенями привода, пользуясь соотношениями, приведенными в таблице 1.3 [1]:
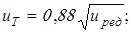
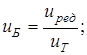
где 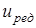 – передаточное число редуктора, в нашем случае равное – передаточное число редуктора, в нашем случае равное 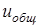 . .
Вычисляем передаточные отношения ступеней
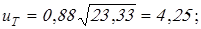
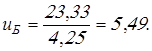
Частота вращения вала колеса тихоходной ступени 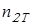
 . .
Частота вращения вала колеса быстроходной ступени 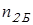
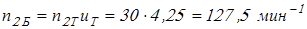 . .
Момент на приводном валу 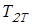
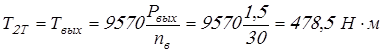 . .
Момент на валу колеса быстроходной ступени редуктора 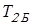
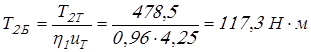 . .
3.1 Выбор твердости, термической обработки и материала колес
Для колес быстроходной ступени выберем сталь 40ХН и термическую обработку по II варианту [1] – т.о. колеса – улучшение, твердость HB 269…302; т.о. шестерни – улучшение и закалка ТВЧ, твердость поверхности HRC 48…53.
Для колес тихоходной ступени выберем тоже сталь 40ХН и термическую обработку по I варианту [1] – т.о. колеса – улучшение, твердость HB 235…262; т.о. шестерни – улучшение, твердость HB 269…302.
Расчет передач проведем по допускаемым напряжениям
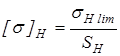
и 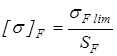
соответствующим длительной контактной и изгибной выносливостям:
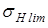 и и 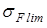 – пределы выносливостей; – пределы выносливостей;
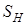 и и 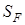 – коэффициенты безопасности по контактным (индекс ) и изгибным (индекс F) напряжениям. – коэффициенты безопасности по контактным (индекс ) и изгибным (индекс F) напряжениям.
Допускаемые контактные напряжения и напряжения изгиба определим отдельно для колеса  , , 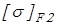 и шестерни и шестерни 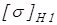 , , 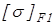 . .
Значения  и и 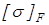 принимаем по таблице 2.2 [1], в которой принимаем по таблице 2.2 [1], в которой 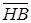 и и 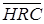 – средняя твердость для двух предельных значений, приведенных в вариантах т.о. и в таблице 2.1. – средняя твердость для двух предельных значений, приведенных в вариантах т.о. и в таблице 2.1.
Для тихоходной ступени принимаем
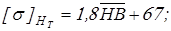
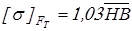 , ,
и получаем следующие значения
для колеса
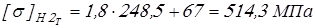 ; ;
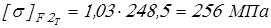 , ,
для шестерни
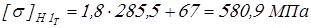 ; ;
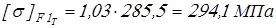 , ,
для быстроходной ступени принимаем
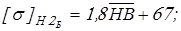
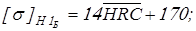
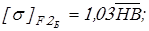
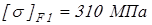 , ,
и получаем следующие значения
для колеса
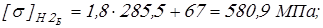
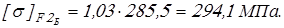
для шестерни
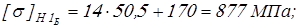
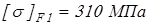 . .
Для зубчатых передач при II варианте т.о. определяют расчетное допускаемое контактное напряжение
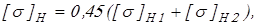
это напряжение не должно превышать  . .
Вычисляем
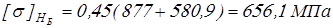
условие
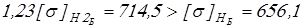 . .
выполняется. В расчетную формулу вместо 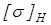 подставим меньшее из значений подставим меньшее из значений 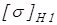 и и  , следовательно, для дальнейших расчетов будем использовать, следующие значения допустимых напряжений: , следовательно, для дальнейших расчетов будем использовать, следующие значения допустимых напряжений:
для тихоходной ступени
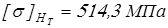 ; ;
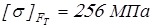 , ,
для быстроходной ступени
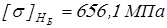 ; ;
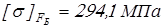 . .
Межосевое расстояние определяется по формуле:
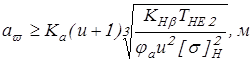
где коэффициент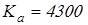 – для косозубых колес. – для косозубых колес.
Коэффициент концентрации нагрузки 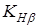 принимаем для прирабатывающихся колес при переменной нагрузке: принимаем для прирабатывающихся колес при переменной нагрузке:
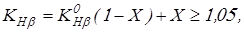
где  – начальный коэффициент концентрации нагрузки; – начальный коэффициент концентрации нагрузки;
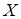 – коэффициент режима нагрузки. – коэффициент режима нагрузки.
При ступенчатом графике режима нагружения коэффициент 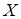 вычисляем по формуле: вычисляем по формуле:
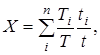
где 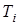 – момент при i-м режиме нагружения; – момент при i-м режиме нагружения;
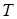 – наибольший момент из числа длительно действующих; – наибольший момент из числа длительно действующих;
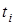 – время работы передачи (ч) при i-м режиме; – время работы передачи (ч) при i-м режиме;
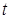 – время работы передачи, ч. – время работы передачи, ч.
Вычисляем коэффициент режима нагрузки
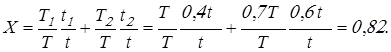
Начальный коэффициент концентрации нагрузки  принимаем по таблице 2.3 [1] в зависимости от коэффициента принимаем по таблице 2.3 [1] в зависимости от коэффициента 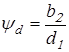 . Так как ширина колеса . Так как ширина колеса 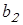 и диаметр шестерни и диаметр шестерни 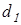 ещё не определены, коэффициент ещё не определены, коэффициент 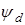 определяем ориентировочно: определяем ориентировочно:
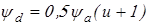 , ,
где коэффициент 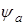 принимаем из ряда стандартных чисел в зависимости от положения колес относительно опор, равным: принимаем из ряда стандартных чисел в зависимости от положения колес относительно опор, равным:
для тихоходной передачи, при консольной расположении колес
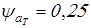 , ,
для быстроходной передачи, при симметричном расположении колес
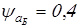 . .
Вычисляем коэффициенты для передач:
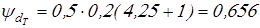 ; ;

По таблице 2.3 [1] в зависимости от коэффициента 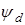 находим находим  . .
Получаем
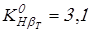 ; ;
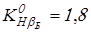 . .
При коэффициенте 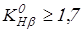 целесообразно применять колеса с бочкообразными зубьями, для которых целесообразно применять колеса с бочкообразными зубьями, для которых 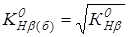 , тогда получим , тогда получим
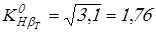 ; ;
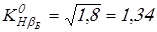 . .
Вычисляем коэффициенты концентрации нагрузки
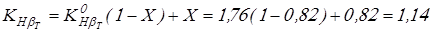 ; ;
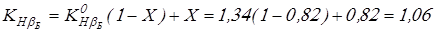 . .
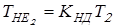 – эквивалентный момент на колесе, где – эквивалентный момент на колесе, где
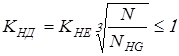 – коэффициент долговечности. – коэффициент долговечности.
Здесь: 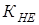 – коэффициент эквивалентности, зависящий от режима нагружения; – коэффициент эквивалентности, зависящий от режима нагружения; 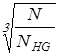 – коэффициент циклов, учитывающий различие в числе циклов нагружений зубчатых колес в разных ступенях передач; – коэффициент циклов, учитывающий различие в числе циклов нагружений зубчатых колес в разных ступенях передач; 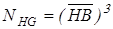 – базовое число циклов нагружений. – базовое число циклов нагружений.
При ступенчатом графике режима нагружения коэффициент эквивалентности
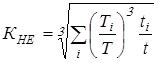 , ,
где 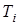 ; ; 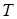 ; ; 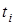 и и 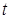 определяются также как и при вычислении коэффициента режима определяются также как и при вычислении коэффициента режима 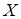 . .
Базовое число циклов нагружения
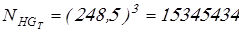 ; ;
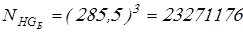 . .
Число циклов нагружения
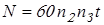 , ,
где 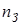 – число зацеплений колеса; – число зацеплений колеса;
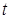 – время работы передачи, определяется так – время работы передачи, определяется так
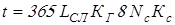 , ,
где 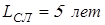 – срок службы привода; – срок службы привода;
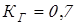 – коэффициент годовой загрузки привода; – коэффициент годовой загрузки привода;
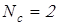 – сменность работы привода; – сменность работы привода;
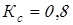 – коэффициент сменной загрузки привода. – коэффициент сменной загрузки привода.
Вычисляем числа циклов нагружения

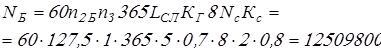
Вычисляем коэффициент эквивалентности
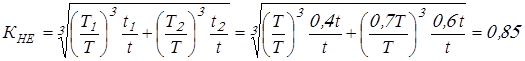 . .
Вычисляем коэффициенты долговечности
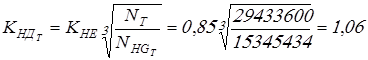 , принимаем , принимаем 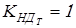 ; ;
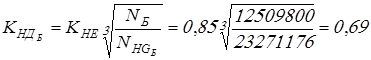 . .
Вычисляем эквивалентные моменты на колесах
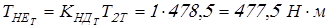 ; ;
 . .
Вычисляем межосевые расстояния

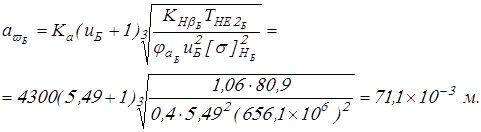
Вычисленные межосевые расстояния округляем в большую сторону до стандартных значений и окончательно получаем:
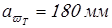 ; ;
 . .
Делительный диаметр зубчатых колес
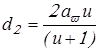 ; ;
 . .
Ширина зубчатых колес
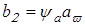 . .
Вычисляем основные размеры колес
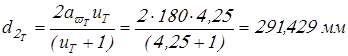 ; ;
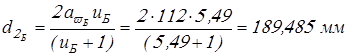 ; ;
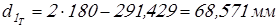 ; ;
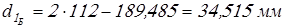 ; ;
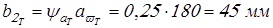 ; ;
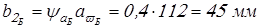 . .
Диаметры различных участков валов редуктора определим по формулам:
для быстроходного вала
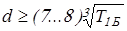 ; ;
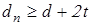 ; ;
 , ,
для промежуточного вала
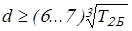 ; ;
 ; ;
 ; ;
 ; ;
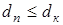 , ,
для тихоходного вала
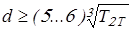 ; ;
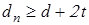 ; ;
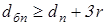 ; ;
 , ,
где 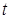 – высота буртика; – высота буртика;
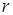 – фаска подшипника; – фаска подшипника;
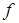 – размер фаски – размер фаски
принимаемые в зависимости от диаметра  посадочной поверхности. посадочной поверхности.
Вычисляем диаметры валов и округляем их в ближайшую сторону до стандартных значений:
быстроходный вал
 принимаем принимаем 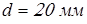 ; ;
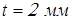 ; ;
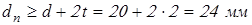 принимаем принимаем  ; ;
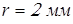 ; ;
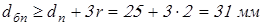 принимаем принимаем 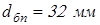 , ,
для промежуточного вала
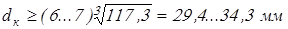 принимаем принимаем 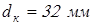 ; ;
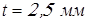 ; ;
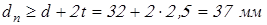 принимаем принимаем  ; ;
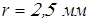 ; ;
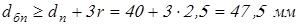 принимаем принимаем 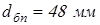 ; ;
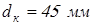 . .
тихоходный вал
 принимаем принимаем 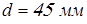 ; ;
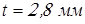 ; ;
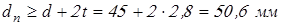 принимаем принимаем 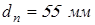 ; ;
 ; ;
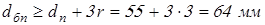 принимаем принимаем 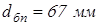 ; ;
 . .
Модуль передач определим по формуле:
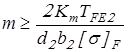 , ,
где коэффициент 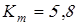 – для косозубых колес. – для косозубых колес.
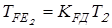 – эквивалентный момент на колесе, – эквивалентный момент на колесе,
где 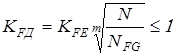 – коэффициент долговечности. – коэффициент долговечности.
Здесь: 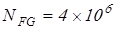 – базовое число циклов – базовое число циклов
При ступенчатом графике режима нагружения коэффициент эквивалентности
 , ,
где  при т.о. колес – улучшение. при т.о. колес – улучшение.
Вычисляем коэффициент эквивалентности 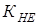
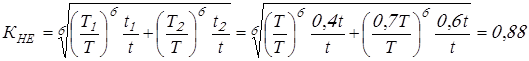
Вычисляем коэффициенты долговечности 
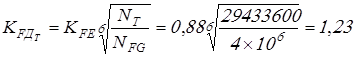 , принимаем , принимаем 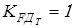 ; ;
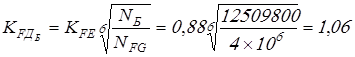 , принимаем , принимаем 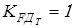 . .
Вычисляем эквивалентные моменты на колесах 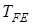
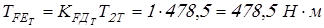 ; ;
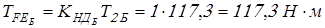 . .
Вычисляем модули передач
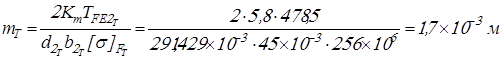 ; ;
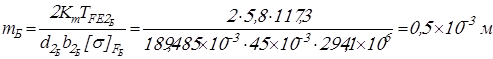 . .
Значения модуля, полученные расчетом, округляем до стандартной величины и получаем
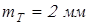 ; ;
 . .
Минимальный угол наклона зубьев косозубых колес
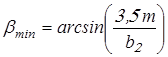
Вычисляем
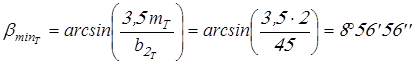 ; ;
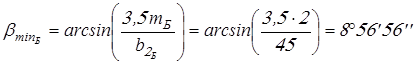 . .
Суммарное число зубьев

Вычисляем суммарное число зубьев
 ; ;
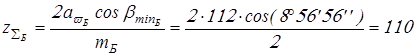 . .
Определяем действительное значение угла
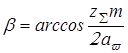 ; ;
Вычисляем
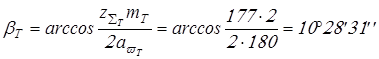 ; ;
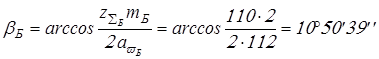 . .
Число зубьев шестерни
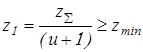
Вычисляем числа зубьев шестерен
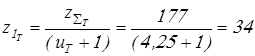 ; ;
 . .
Для косозубых колес 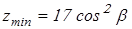
Вычисляем минимально допустимое число зубьев
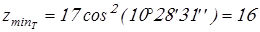 ; ;
 . .
Условие
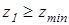
выполняется для обеих передач.
Число зубьев колеса

Вычисляем числа зубьев колес
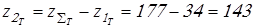 ; ;
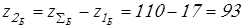 . .
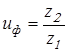
Вычисляем фактические передаточные числа
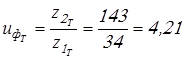 ; ;
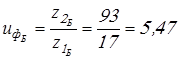 . .
Общее передаточное число привода
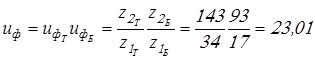
Отклонение от заданного передаточного числа
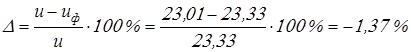
Условие
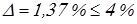
выполняется.
Делительные диаметры 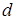 : :
шестерни
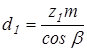 ; ;
колеса
 ; ;
Диаметры окружностей вершин 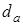 и впадин и впадин 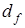 зубьев зубьев
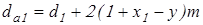 ; ;
 ; ;
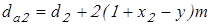 ; ;
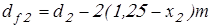 , ,
где 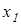 и и 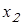 – коэффициенты смещения у шестерни и колеса; – коэффициенты смещения у шестерни и колеса; 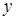 – коэффициент воспринимаемого смещения. – коэффициент воспринимаемого смещения.
Вычисляем диаметры колес и полученные результаты заносим в таблицу 1.
Делительные диаметры шестерен 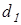
 ; ;
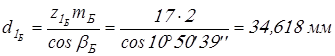 . .
Делительные диаметры колес 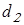
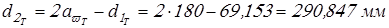 ; ;
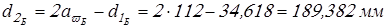 . .
Диаметры окружностей вершин зубьев 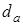
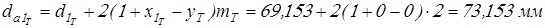 ; ;
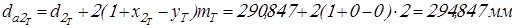 ; ;
 ; ;
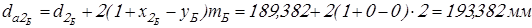 . .
Диаметры впадин 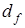
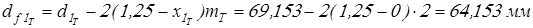 ; ;
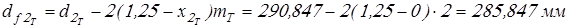 ; ;
 ; ;
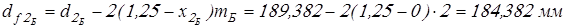 . .
Параметры зубчатых колес Таблица 1
| Параметр |
 |
 |
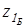 |
 |
| Число зубьев |
|
|
|
|
| Модуль, мм |
|
|
| Угол наклона, град |
¢¢¢ |
¢¢¢ |
| Делительный диаметр, мм |
|
|
|
|
| Диаметр впадин, мм |
|
|
|
|
| Диаметр вершин зубьев, мм |
|
|
|
|
| Межосевое расстояние, мм |
|
|
| Ширина венца, мм |
|
|
3.11 Размеры заготовок колес
Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, вычислим предельные размеры заготовок и проверим выполнение условий
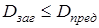 ; ;
 ; ;
Диаметр заготовки
 ; ;
для колеса с выточками принимаем меньшее из
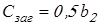 ; ;
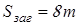 , ,
для колеса без выточек
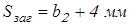 . .
По таблице 2.1 [1] находим следующие предельные размеры заготовок
электродвигатель привод вал
для 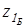 , ,  , , 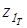 – – 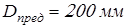 ; ; 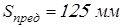 ; ;
для  – – 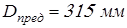 ; ; 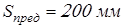 . .
Вычисляем размеры заготовок
для 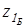 (без выточки) (без выточки)
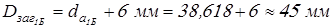 ; ;
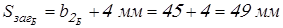 , ,
для  (с выточкой) (с выточкой)
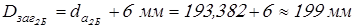 ; ;
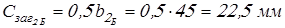 , ,
для 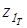 (без выточки) (без выточки)
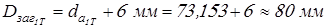 ; ;
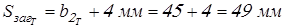 , ,
для  (с выточкой) (с выточкой)
 ; ;
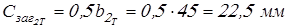
проверяем условия 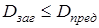 и и  – все выполняются. – все выполняются.
Окружная сила 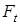
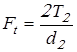 ; ;
Радиальная сила 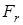
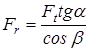 ; ;
Осевая сила 
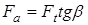 . .
Вычислим уточненные крутящие моменты и частоты вращения
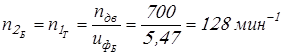 ; ;
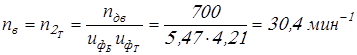 ; ;
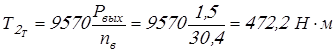 ; ;
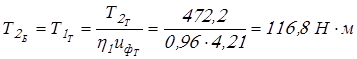 ; ;
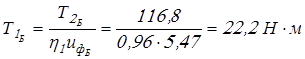 ; ;
Вычисляем силы в зацеплениях и результаты заносим в таблицу 2.
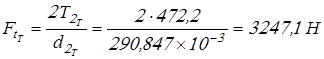 ; ;
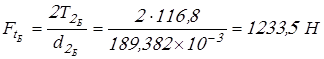 ; ;
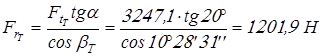 ; ;
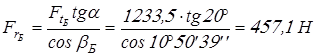 ; ;
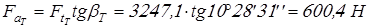 ; ;
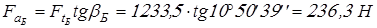 . .
Силы в зацеплении, в Н Таблица 2
| Ступень |
Окружная сила 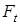 , Н , Н |
Радиальная сила 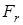 , Н , Н |
Осевая сила  , Н , Н |
Крутящий момент  , Н·м , Н·м |
Частота вращения 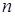 , мин-1 , мин-1 |
| Быстроходная |
|
|
|
|
|
| Тихоходная |
|
|
|
|
|
3.13 Проверка зубьев колес по напряжениям изгиба
Расчетное напряжение изгиба в зубьях колеса определим по формуле
 ; ;
в зубьях шестерни по формуле
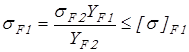 . .
Степень точности передач принимаем по таблице 2.5 [1] в зависимости от окружной скорости колеса (м/с)
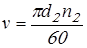 ; ;
Вычисляем окружные скорости колес
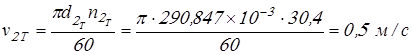 ; ;
 . .
По таблице 2.5 [1] принимаем 9-ю степень точности для всех колес.
Для косозубых колес при выбранной степени точности коэффициент 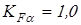 . .
Коэффициент концентрации нагрузки 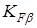 принимаем для прирабатывающихся колес по формуле принимаем для прирабатывающихся колес по формуле
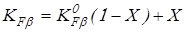 , ,
где 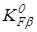 – начальный коэффициент концентрации нагрузки; – начальный коэффициент концентрации нагрузки;
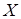 – коэффициент режима. – коэффициент режима.
По таблице 2.6 [1] в зависимости от 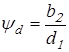 принимаем принимаем
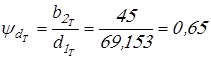 ; ; 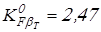 ; ;
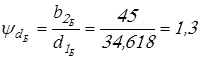 ; ; 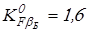 . .
Вычисляем коэффициенты концентрации нагрузки 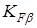
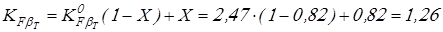 ; ;
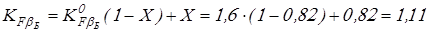 . .
Коэффициент динамической нагрузки 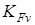 принимаем по таблице 2.7 [1] принимаем по таблице 2.7 [1]
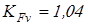 . .
Коэффициент 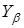 вычисляют по формуле вычисляют по формуле
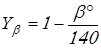 . .
Вычисляем коэффициенты 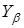
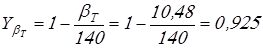 ; ;
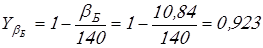 . .
Коэффициенты формы зуба 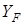 принимаем по таблице 2.8 [1] принимаем по таблице 2.8 [1]
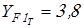 ; ; 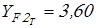 ; ;
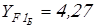 ; ; 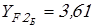 . .
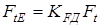 – эквивалентная окружная сила. – эквивалентная окружная сила.
Вычисляем эквивалентную окружную силу 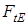
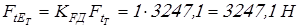 ; ;
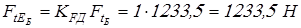 . .
Вычисляем напряжения изгиба действующие в передачах
для колес
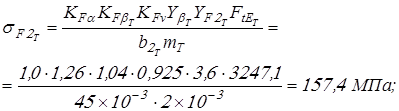

для шестерен
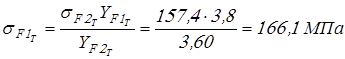 ; ;
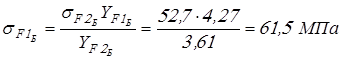 . .
Все условия
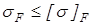
выполняются.
Проверим зубья колес на статическую прочность по кратковременно действующим пиковым моментам 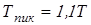

Значение 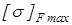 берем из таблицы 2.2 [1] берем из таблицы 2.2 [1]
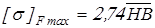 – при т.о. колеса улучшение; – при т.о. колеса улучшение;
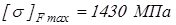 – при сквозной закалке зубьев ТВЧ. – при сквозной закалке зубьев ТВЧ.
Получаем
для 
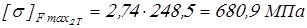 ; ;
для 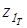 и и 
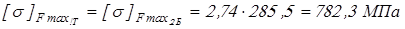 ; ;
для 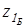
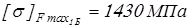 . .
Вычисляем напряжения изгиба при кратковременно действующих пиковых моментах
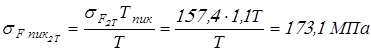 ; ;
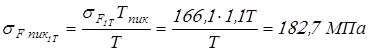 ; ;
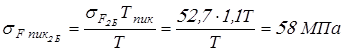 ; ;
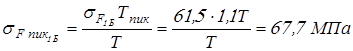 . .
Все условия
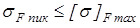
выполняются.
Расчетное контактное напряжение определим по формуле
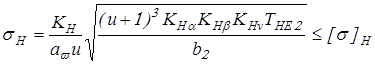 , ,
где для косозубых колес 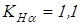 ; ;  . Коэффициент . Коэффициент 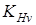 принимаем по таблице 2.9 [1] и получаем принимаем по таблице 2.9 [1] и получаем
 . .
Вычисляем контактные напряжения, действующие в колесах

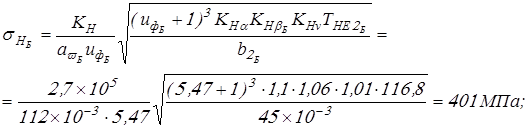
Условия
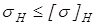
выполняются.
Проверим зубья колес на статическую прочность при кратковременных действующих пиковых моментах 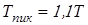 по формуле по формуле
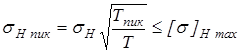 . .
Значения 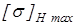 берем из таблицы 2.2 [1] берем из таблицы 2.2 [1]
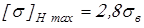 – при т.о. колеса улучшение; – при т.о. колеса улучшение;
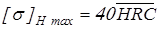 – при сквозной закалке зубьев ТВЧ. – при сквозной закалке зубьев ТВЧ.
Получаем
для 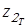
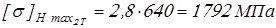 , ,
для 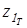 и и 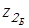
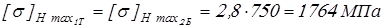 , ,
для 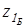
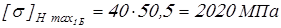 . .
Вычисляем контактные напряжения при кратковременно действующих пиковых моментах
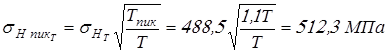 ; ;
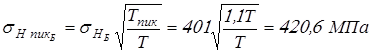 . .
Все условия
выполняются.
Чтобы поверхности вращающихся колес не задевали за внутренние поверхности стенок корпуса, между ними оставляют зазор 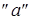 , который определяют по формуле , который определяют по формуле
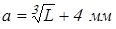 , ,
где 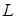 – наибольшее расстояние между внешними поверхностями деталей передач, мм. – наибольшее расстояние между внешними поверхностями деталей передач, мм.
Вычисляем зазор 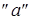
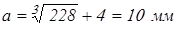 . .
Толщину стенки 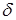 , отвечающую требованиям технологии литья и необходимой жесткости корпуса редуктора, рекомендуется определять по формуле , отвечающую требованиям технологии литья и необходимой жесткости корпуса редуктора, рекомендуется определять по формуле
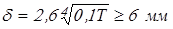 , ,
где 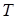 – вращающий момент на тихоходном валу, – вращающий момент на тихоходном валу, 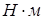 . .
Вычисляем толщину стенки 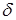
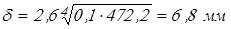 принимаем принимаем 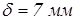 . .
Радиусы для сопряжения стенок корпуса редуктора определим по соотношению
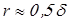 ; ; 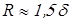
где 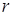 – радиус внутреннего сопряжения, а – радиус внутреннего сопряжения, а 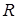 – наружного. – наружного.
Вычисляем радиусы 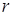 и и 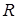
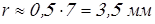 ; ; 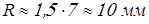 . .
Предварительно выберем для обеих опор роликовые конические подшипники средней серии  со следующими характеристиками: со следующими характеристиками: 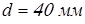 ; ; 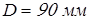 ; ; 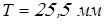 ; ; 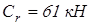 ; ; 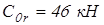 ; ; 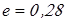 ; ;  ; ; 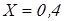 . .
Требуемая долговечность подшипников в часах
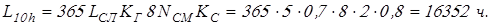
полученное значение округляем по таблице 70 [3] до 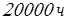 . .
Радиальная реакция подшипника 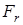 считается приложенной к оси вала в точке пересечения с ней нормалей, проведенных через середины контактных площадок. Для роликовых конических подшипников расстояние «а» между этой точкой и торцом подшипника определяется по формуле: считается приложенной к оси вала в точке пересечения с ней нормалей, проведенных через середины контактных площадок. Для роликовых конических подшипников расстояние «а» между этой точкой и торцом подшипника определяется по формуле:
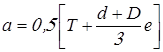 , ,
где 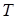 – монтажная высота кольца; – монтажная высота кольца;
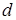 – диаметр внутреннего кольца подшипника; – диаметр внутреннего кольца подшипника;
 – диаметр наружного кольца подшипника; – диаметр наружного кольца подшипника;
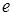 – коэффициент осевого нагружения. – коэффициент осевого нагружения.
Вычисляем расстояние «а»
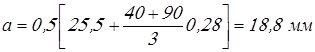 . .
С учетом монтажной высоты кольца  и расстояния «а» построим расчетную схему для определения радиальных сил действующих на подшипники (рис. 3). и расстояния «а» построим расчетную схему для определения радиальных сил действующих на подшипники (рис. 3).
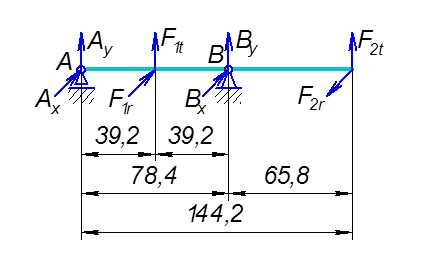
Рис. 3. Схема к определению реакций опор
Приведем плоскости действия известных сил к двум взаимно перпендикулярным плоскостям. Реакции опор определим из условия равновесия всех сил относительно каждой опоры.
Плоскость X–X
 ; ;
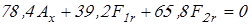 , откуда реакция , откуда реакция  равна равна
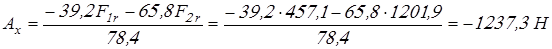 . .
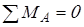 ; ;
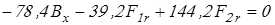 , откуда реакция , откуда реакция  равна равна
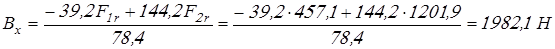 . .
Плоскость Y–Y
 ; ;
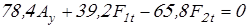 , откуда реакция , откуда реакция 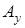 равна равна
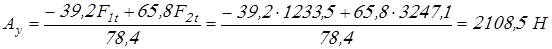 . .
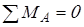 ; ;
 , откуда реакция , откуда реакция 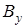 равна равна
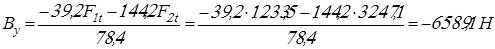 . .
Результирующие радиальные силы, максимально длительно действующие на подшипники, вычислим по формуле
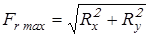 , ,
где 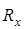 и и 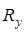 – соответственно горизонтальная и вертикальная составляющие радиальной силы. – соответственно горизонтальная и вертикальная составляющие радиальной силы.
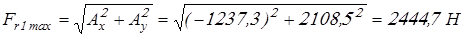 ; ;
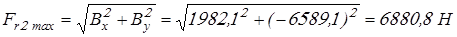 . .
5.2 Определение осевых нагрузок
Результирующая осевая сила, действующая на подшипники от косозубых зубчатых колес равна
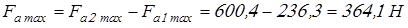 . .
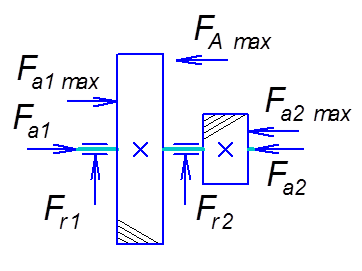
Рис. 4. Схема нагружения подшипников
При установке вала на радиально-упорных подшипниках осевые силы  , нагружающие подшипники, находят с учетом осевых составляющих S от действия радиальных сил , нагружающие подшипники, находят с учетом осевых составляющих S от действия радиальных сил  : :
для конических роликовых подшипников
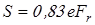 , ,
где 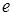 – коэффициент осевой нагрузки. – коэффициент осевой нагрузки.
Вычисляем осевые составляющие 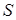
 ; ;
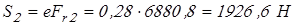 . .
В таблице 7.2 [1] исходя из условий нагружения 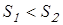 ; ;  получаем формулы для вычисления получаем формулы для вычисления 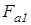 и и  : :
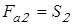 ; ;
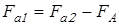 . .
Вычисляем осевые силы  , нагружающие подшипники , нагружающие подшипники
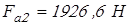 ; ;
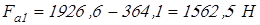 . .
Эквивалентную динамическую нагрузку 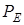 для подшипников определим по формуле для подшипников определим по формуле
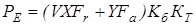 , ,
где  и и  – коэффициенты радиальной и осевой нагрузок; – коэффициенты радиальной и осевой нагрузок;
 – коэффициент вращения; – коэффициент вращения;
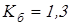 – коэффициент безопасности; – коэффициент безопасности;
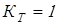 – коэффициент, зависящий от рабочей температуры подшипника. – коэффициент, зависящий от рабочей температуры подшипника.
Вычисляем эквивалентные динамические нагрузки 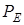
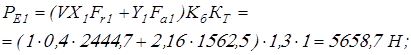

Требуемую грузоподъёмность подшипников определим по самой нагруженной опоре 2 по формуле
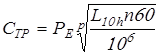 , ,
где 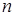 – частота вращения кольца, мин-1; – частота вращения кольца, мин-1;
для роликовых подшипников 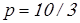 . .
Требуемая грузоподъёмность подшипников  равна равна
 . .
Так как
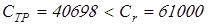 , ,
то предварительно намеченный подшипник подходит.
При расчете примем, что насаженные на вал детали передают силы и моменты валу на середине своей ширины.
Под действием постоянных по величине и направлению сил во вращающихся валах возникают напряжения, изменяющиеся по симметричному циклу.
Построим расчетную схему для II вала: нанесем на неё все внешние силы нагружающие вал (рис. 5).
Расчет произведем в форме проверки коэффициента запаса прочности. Для каждого из установленных предположительно опасных сечений определим расчетный коэффициент запаса прочности «S» и сравним его с допускаемым значением [S], которое обычно принимают [S]=1,3…2.
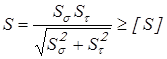 , ,
где 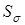 и и 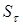 – коэффициенты запаса по нормальным и касательным напряжениям, определяемые по зависимостям: – коэффициенты запаса по нормальным и касательным напряжениям, определяемые по зависимостям:
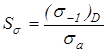 – для напряжений изменяющихся по симметричному циклу. – для напряжений изменяющихся по симметричному циклу.
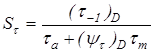
Здесь 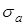 и и 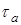 – амплитуды напряжений цикла; – амплитуды напряжений цикла;
 – среднее напряжение цикла. – среднее напряжение цикла.
 ; ; 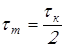 . .
Напряжение в опасных сечениях определим по формулам
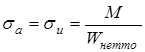 ; ; 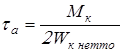 , ,
где 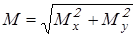 – результирующий изгибающий момент; – результирующий изгибающий момент;
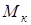 – крутящий момент; – крутящий момент;
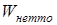 и и 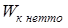 – осевой и полярный моменты сопротивления сечения вала. – осевой и полярный моменты сопротивления сечения вала.
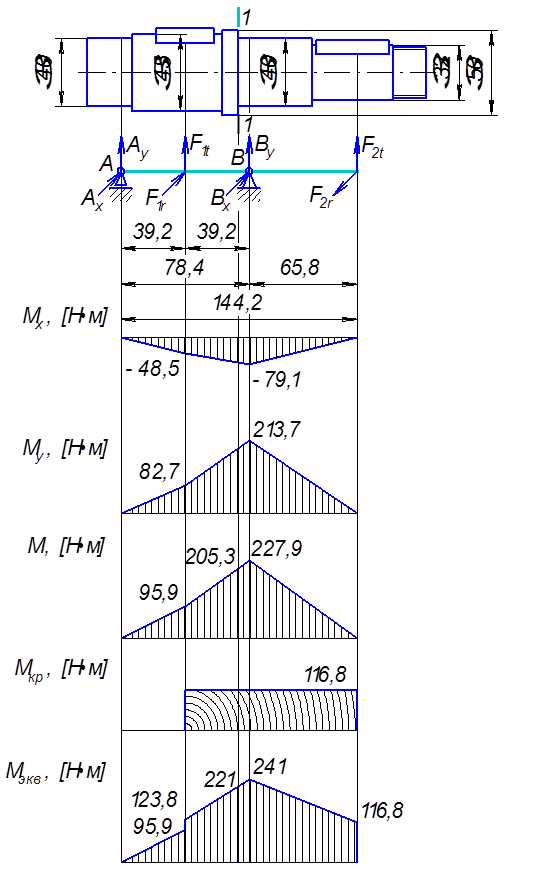
Рис. 5. Расчетная схема II вала
Пределы выносливости вала в рассматриваемом сечении
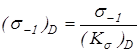 ; ;
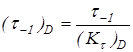
где 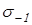 и и 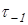 – пределы выносливости гладких образцов при симметричном цикле изгиба и кручения; – пределы выносливости гладких образцов при симметричном цикле изгиба и кручения;
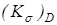 и и  – коэффициенты концентрации напряжений для данного сечения вала. – коэффициенты концентрации напряжений для данного сечения вала.
Значения 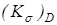 и и  находят по зависимостям: находят по зависимостям:
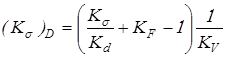 ; ;
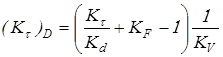 , ,
где  и и 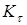 – эффективные коэффициенты концентрации напряжений; – эффективные коэффициенты концентрации напряжений;
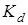 – коэффициент влияния абсолютных размеров поперечного сечения; – коэффициент влияния абсолютных размеров поперечного сечения;
 – коэффициент влияния шероховатости; – коэффициент влияния шероховатости;
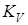 – коэффициент влияния поверхностного упрочнения. – коэффициент влияния поверхностного упрочнения.
Коэффициент влияния асимметрии цикла для рассматриваемого сечения вала
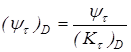 , ,
где 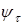 – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.
По эпюрам эквивалентного момента 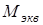 (рис. 5) видно, что самым опасным сечением является сечение 1–1. (рис. 5) видно, что самым опасным сечением является сечение 1–1.
Материал вала выберем сталь 45 со следующими характеристиками: HB270, 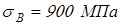 ; ;  ; ; 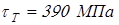 ; ; 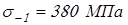 ; ; 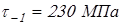 ; ; 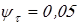 . .
Осевой 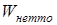 и полярный и полярный 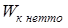 моменты сопротивления сечения 1‑1 моменты сопротивления сечения 1‑1
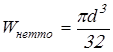 ; ;
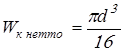 . .
где 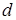 – диаметр сечения равный 40 мм. – диаметр сечения равный 40 мм.
Вычисляем моменты сопротивления
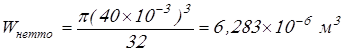 ; ;
 . .
Вычисляем напряжения в опасном сечении
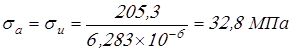 ; ;
 , ,
По таблицам 10.3…10.6 [1] находим значения следующих коэффициентов
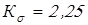 ; ; 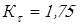 ; при ; при 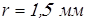 ; ; 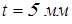 . .
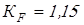 ; при ; при 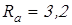 . .
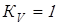 – без упрочнения. – без упрочнения.
Вычисляем коэффициенты концентрации напряжений
при 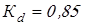
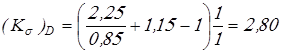 ; ;
при 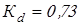
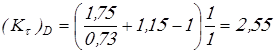 . .
Вычисляем коэффициент влияния асимметрии цикла
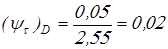 . .
Вычисляем пределы выносливости вала в рассматриваемом сечении
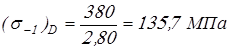 ; ;
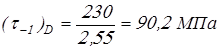 . .
Вычисляем коэффициенты запаса по нормальным и касательным напряжениям
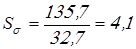 ; ;
 . .
Вычисляем коэффициент запаса прочности
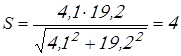 . .
Запас прочности обеспечен достаточный так как
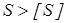 . .
Рекомендуется назначать одинаковые шпонки для всех ступеней вала исходя из ступени наименьшего диаметра, имеющего шпоночный паз. Наличие на одном валу шпоночных пазов, одинаковых по сечению и длине, улучшает технологичность конструкции вала.
Предварительно выберем сечение шпонки, рекомендуемое ГОСТ 23360‑78, исходя из величины диаметра вала.
Получаем шпонку 12´8´40 ГОСТ 23360‑78.
Проверим рабочие грани шпонки на смятие. Условие прочности на смятие
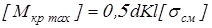 , ,
где 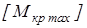 – наибольший допускаемый крутящий момент; – наибольший допускаемый крутящий момент;
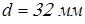 – диаметр вала; – диаметр вала;
 – рабочая длина шпонки; – рабочая длина шпонки;
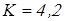 – выступ шпонки от шпоночного паза; – выступ шпонки от шпоночного паза;
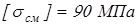 – допускаемое напряжение на смятие. – допускаемое напряжение на смятие.
Вычисляем наибольший допускаемый крутящий момент 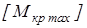

так как наибольший продолжительно действующий крутящий момент на валу 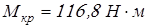 , то выбранная шпонка проходит проверку на смятие , то выбранная шпонка проходит проверку на смятие
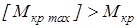
Проверим шпонку на срез. Условие прочности сечения шпонки на срез
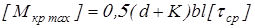 , ,
где 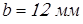 – ширина шпонки; – ширина шпонки;
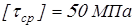 – допускаемое напряжение на срез. – допускаемое напряжение на срез.
Вычисляем наибольший допускаемый крутящий момент 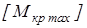
 , ,
так как 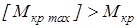 , то выбранная шпонка проходит проверку на срез. , то выбранная шпонка проходит проверку на срез.
1. Дунаев П. Ф., Леликов О. П. Конструирование узлов и деталей машин. ‑М.: Высшая школа, 1985.
2. Асинхронные двигатели серии 4А: Справочник/ под ред. Кравчика А. Э., Шлафа М. М. и др. ‑М.: Энергоиздат, 1982.
3. Справочник конструктора-машиностроителя/ под ред. Анурьева В. И. т. 2 – М.: Машиностроение, 1982.
|