1. Численные методы решения систем линейных уравнений
.
1.1 Заданная система

1.2 Метод Гаусса
 (1.1.) (1.1.)
Прямой ход
Нормируем первое уравнение системы, разделив все члены уравнения на его первый коэффициент при  : :
 (1.2.) (1.2.)
Умножим нормированное уравнение (1.2) на коэффициенты при х1
оставшихся уравнений системы (1.1).
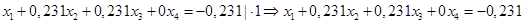 (1.3.) (1.3.)
 (1.4.) (1.4.)
 (1.5.) (1.5.)
Вычтем полученные уравнения (1.3.), (1.4.), (1.5.) из второго, третьего и четвёртого уравнения системы (1.1.) соответственно, чтобы исключить из системы х1
:

 (1.6.)
(1.6.)
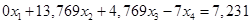
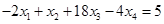
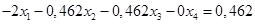 (1.7.)
(1.7.)

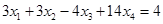
 (1.8.)
(1.8.)

Получим новую систему уравнений:
 (1.9.) (1.9.)
Рассмотрим систему уравнений (1.9).
Решим систему уравнений без первого уравнения системы (1.9.).
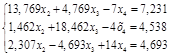 (1.10.) (1.10.)
Нормируем первое уравнение системы (1.10.), разделив все члены уравнения на коэффициент при 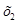 : :
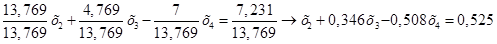 (1.11.) (1.11.)
Умножаем нормированное уравнение (1.11.) на коэффициент при х2
оставшихся уравнений:
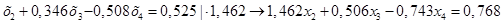 (1.12.) (1.12.)
 (1.13.) (1.13.)
Вычтем полученные уравнения (1.12.), (1.13.) из второго и третьего уравнения системы (1.10.) соответственно, чтобы исключить из системы х2
:
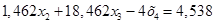
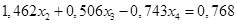 (1.14.)
(1.14.)
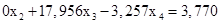

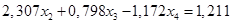 (1.15.)
(1.15.)
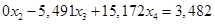
Получим новую систему уравнений:
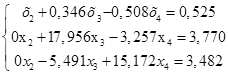 (1.16.) (1.16.)
Рассмотрим систему (1.16) без первого уравнения:
 (1.17.) (1.17.)
Нормируем первое уравнение системы (1.17.).
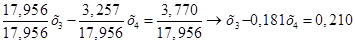 (1.18.) (1.18.)
Умножаем полученное уравнение (1.18.) на коэффициент при х4
второго уравнения системы (1.17.):
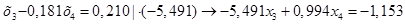 (1.19.) (1.19.)
Вычтем полученное уравнение (1.19.) из второго уравнения системы (1.18.):
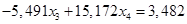
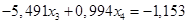 (1.20.)
(1.20.)
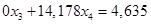
Получим новую систему линейных уравнений:
 (1.21.) (1.21.)
Рассмотрим последнее уравнение системы (1.21.).
Нормируем данное уравнение:
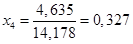 (1.22.) (1.22.)
В результате выполненных действий система (1.1.) приведена к треугольному виду:
 (1.23.) (1.23.)
Обратный ход
x4
= 0,327;
Найдём 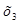 из третьего уравнения системы (1.23.): из третьего уравнения системы (1.23.):
x3
= 0,210+0,181·0,327=0,269;
Найдём 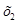 из второго уравнения системы (1.23.): из второго уравнения системы (1.23.):
x2
= 0,525–0,346·0,269+0,508·0,327 = 0,598;
Найдём  из первого уравнения системы (1.23.): из первого уравнения системы (1.23.):
x1
= -0,231–0,231·0,598–0,231·0,269+0·0,327 = -0,431
Решением системы линейных уравнений являются значения неизвестных:
Ответ:
x1
= -0,431;
x2
= 0,598;
x3
= 0,269;
x4
= 0,327.
1.3 Метод простой итерации

Выполним проверку на сходимость
|a11
|>|a12
|+|a13
|+|a14
| → |13|>|3|+|3|+|0|
|a22
|>|a21
|+|a23
|+|a24
| → |14|>|1|+|5|+|-7|
|a33
|>|a31
|+|a32
|+|a34
| → |18|>|-2|+|1|+|-4|
|a44
|>|a41
|+|a42
|+|a43
| → |14|>|3|+|3|+|-4|
Условия сходимости выполняются, следовательно, решение может быть найдено с определенной точностью за некоторое число итераций.
Вычислим значения неизвестных системы линейных алгебраических уравнений с точностью ε  0,001. 0,001.
Примем за нулевое приближение
неизвестных значения, равные нулю, т.е.
x1
(0)
= 0; x2
(0)
= 0; x3
(0)
= 0; x4
(0)
= 0;
Подставим полученные значения в итерационные формулы и вычислим значения неизвестных при первом приближении.
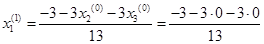 = -0,231 = -0,231
 = 0,500 = 0,500
 = 0,278 = 0,278
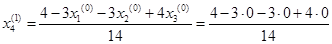 = 0,286 = 0,286
Выполним проверку полученных значений:
|x1
(1)
-x1
(0)
| = |-0,231–0| = 0,231  ε – нет ε – нет
|x2
(1)
-x2
(0)
| = |0,500–0| = 0,500  ε – нет ε – нет
|x3
(1)
-x3
(0)
| = |0,278–0| = 0,278  ε – нет ε – нет
|x4
(1)
-x4
(0)
| = |0,286–0| = 0,286  ε – нет ε – нет
Выполним вторую итерацию.
Подставим значения неизвестных, полученные в первой итерации, в итерационные формулы и вычислим значения неизвестных при втором приближении
.
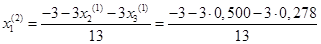 = -0,410 = -0,410
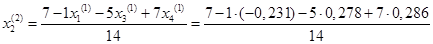 = 0,560 = 0,560
 = 0,288 = 0,288
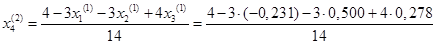 = 0,308 = 0,308
Выполним проверку полученных значений:
|x1
(2)
-x1
(1)
| = |-0,410+0,231| = 0,179  ε – нет, ε – нет,
|x2
(2)
-x2
(1)
| = |0,560–0,500| = 0,060  ε – нет, ε – нет,
|x3
(2)
-x3
(1)
| = |0,288–0,278| = 0,010  ε – нет, ε – нет,
|x4
(2)
-x4
(1)
| = |0,308–0,286| = 0,022  ε – нет. ε – нет.
Выполним третью итерацию.
Подставим значения, полученные во втором приближении, в итерационные формулы и вычислим значения неизвестных при третьем приближении
.
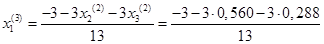 = -0,427 = -0,427
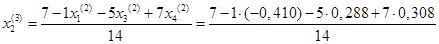 = 0,580 = 0,580
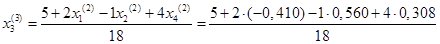 = 0,270 = 0,270
 = 0,336 = 0,336
Выполним проверку полученных значений:
|x1
(3)
-x1
(2)
| = |-0,427+0,410| = 0,017  ε – нет, ε – нет,
|x2
(3)
-x2
(2)
| = |0,580+0,560| = 0,020  ε – нет, ε – нет,
|x3
(3)
-x3
(2)
| = |0,270–0,288| = 0,018  ε – нет, ε – нет,
|x4
(3)
-x4
(2)
| = |0,336–0,308| = 0,028  ε – нет. ε – нет.
Выполним четвёртую итерацию.
Подставим значения, полученные в третьем приближении, в итерационные формулы и вычислим значения неизвестных при четвертом приближении
.
 = -0,427 = -0,427
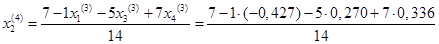 = 0,602 = 0,602
 = 0,273 = 0,273
 = 0,330 = 0,330
Выполним проверку полученных значений:
|x1
(4)
-x1
(3)
| = |-0,427+0,427| = 0,000  ε – да, ε – да,
|x2
(4)
-x2
(3)
| = |0,602–0,580| = 0,022  ε – нет, ε – нет,
|x3
(4)
-x3
(3)
| = |0,273–0,270| = 0,003  ε – нет, ε – нет,
|x4
(4)
-x4
(3)
| = |0,330–0,336| = 0,006  ε – нет. ε – нет.
Выполним пятую итерацию.
Подставим значения, полученные в четвертом приближении, в итерационные формулы и вычислим значения неизвестных при пятом приближении
.
 = -0,433 = -0,433
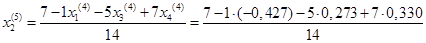 = 0,598 = 0,598
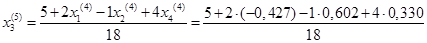 = 0,270 = 0,270
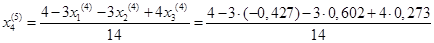 = 0,326 = 0,326
Выполним проверку полученных значений:
|x1
(5)
-x1
(4)
| = |-0,433+0,427| = 0,006  ε – нет, ε – нет,
|x2
(5)
-x2
(4)
| = |0,598–0,602| = 0,004  ε – нет, ε – нет,
|x3
(5)
-x3
(4)
| = |0,270–0,273| = 0,003  ε – нет, ε – нет,
|x4
(5)
-x4
(4)
| = |0,326–0,330| = 0,004  ε – нет. ε – нет.
Выполним шестую итерацию.
Подставим значения, полученные в пятом приближении, в итерационные формулы и вычислим значения неизвестных при шестом приближении
.
 = -0,431 = -0,431
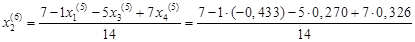 = 0,597 = 0,597
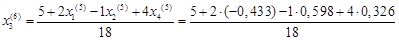 = 0,269 = 0,269
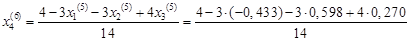 = 0,327 = 0,327
Выполним проверку полученных значений:
|x1
(6)
-x1
(5)
| = |-0,431+0,433| = 0,002  ε – нет, ε – нет,
|x2
(6)
-x2
(5)
| = |0,597–0,598| = 0,001  ε – да, ε – да,
|x3
(6)
-x3
(5)
| = |0,269–0,270| = 0,001  ε – да, ε – да,
|x4
(6)
-x4
(5)
| = |0,327–0,326| = 0,001  ε – да. ε – да.
Выполним седьмую итерацию.
Подставим значения, полученные в шестом приближении, в итерационные формулы и вычислим значения неизвестных при седьмом приближении
.
 = -0,431 = -0,431
 = 0,598 = 0,598
 = 0,269 = 0,269
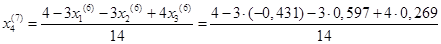 = 0,327 = 0,327
Выполним проверку полученных значений:
|x1
(7)
-x1
(6)
| = |-0,431+0,431| = 0,000  ε – да, ε – да,
|x2
(7)
-x2
(6)
| = |0,598–0,597| = 0,001  ε – да, ε – да,
|x3
(7)
-x3
(6)
| = |0,269–0,269| = 0,000  ε – да, ε – да,
|x4
(7)
-x4
(6)
| = |0,327–0,327| = 0,000  ε – да. ε – да.
Необходимая точность достигается в седьмой итерации.
Ответ:
х1
= -0,431,
х2
= 0,598,
х3
= 0,269,
х4
= 0,327.
1.4 Метод Зейделя

Условия сходимости
было проверено выше, оно выполняется.
Точность вычисления ε  0,001. 0,001.
Примем за нулевое приближение
неизвестных значений, равные нулю.
x1
(0)
= x2
(0)
= x3
(0)
= x4
(0)
= 0;
Подставим полученные значения в итерационные формулы и вычислим значения неизвестных при первом приближении.
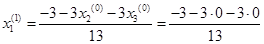 = -0,231 = -0,231
 = 0,517 = 0,517
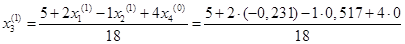 = 0,223 = 0,223
 = 0,288 = 0,288
Выполним проверку полученных значений:
|x1
(1)
-x1
(0)
| = |-0,231–0| = 0,231  ε – нет ε – нет
|x2
(1)
-x2
(0)
| = |0,517–0| = 0,517  ε – нет ε – нет
|x3
(1)
-x3
(0)
| = |0,223–0| = 0,223  ε – нет ε – нет
|x4
(1)
-x4
(0)
| = |0,288–0| = 0,288  ε – нет ε – нет
Выполним вторую итерацию.
Подставим значения, полученные в первом приближении, в итерационные формулы и вычислим значения неизвестных при втором приближении
.
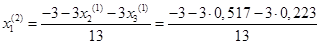 = -0,402 = -0,402
 = 0,593 = 0,593
 = 0,264 = 0,264
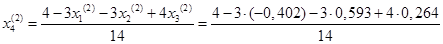 = 0,320 = 0,320
Выполним проверку полученных значений:
|x1
(2)
-x1
(1)
| = |-0,402+0,231| = 0,171  ε – нет, ε – нет,
|x2
(2)
-x2
(1)
| = |0,593–0,517| = 0,076  ε – нет, ε – нет,
|x3
(2)
-x3
(1)
| = |0,264–0,223| = 0,041  ε – нет, ε – нет,
|x4
(2)
-x4
(1)
| = |0,320–0,288| = 0,032  ε – нет. ε – нет.
Выполним третью итерацию.
Подставим значения, полученные во втором приближении, в итерационные формулы и вычислим значения неизвестных при третьем приближении
.
 = -0,429 = -0,429
 = 0,596 = 0,596
 = 0,268 = 0,268
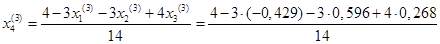 = 0,326 = 0,326
Выполним проверку полученных значений:
|x1
(3)
-x1
(2)
| = |-0,429+0,402| = 0,027  ε – нет, ε – нет,
|x2
(3)
-x2
(2)
| = |0,596–0,593| = 0,003  ε – нет, ε – нет,
|x3
(3)
-x3
(2)
| = |0,268–0,264| = 0,004  ε – нет, ε – нет,
|x4
(3)
-x4
(2)
| = |0,326–0,320| = 0,006  ε – нет. ε – нет.
Выполним четвёртую итерацию.
Подставим значения, полученные в третьем приближении, в итерационные формулы и вычислим значения неизвестных при четвёртом приближении
.
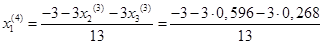 = -0,430 = -0,430
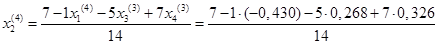 = 0,598 = 0,598
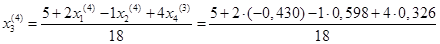 = 0,269 = 0,269
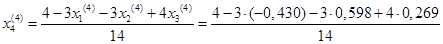 = 0,327 = 0,327
Выполним проверку полученных значений:
|x1
(4)
-x1
(3)
| = |-0,430+0,429| = 0,01  ε – да, ε – да,
|x2
(4)
-x2
(3)
| = |0,598–0,596| = 0,002  ε – нет, ε – нет,
|x3
(4)
-x3
(3)
| = |0,269–0,268| = 0,001  ε – да, ε – да,
|x4
(4)
-x4
(3)
| = |0,327–0,326| = 0,001  ε – да. ε – да.
Выполним пятую итерацию.
Подставим значения, полученные в четвёртом приближении, в итерационные формулы и вычислим значения неизвестных при пятом приближении
.
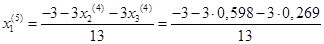 = -0,431 = -0,431
 = 0,598 = 0,598
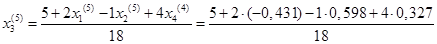 = 0,269 = 0,269
 = 0,327 = 0,327
Выполним проверку полученных значений:
|x1
(5)
-x1
(4)
| = |-0,431+0,430| = 0,001  ε – да, ε – да,
|x2
(5)
-x2
(4)
| = |0,598–0,598| = 0,000  ε – да, ε – да,
|x3
(5)
-x3
(4)
| = |0,269–0,269| = 0,000  ε – да, ε – да,
|x4
(5)
-x4
(4)
| = |0,327–0,327| = 0,000  ε – да. ε – да.
Необходимая точность достигается в пятой итерации.
Ответ:
х1
= -0,431,
х2
= 0,598,
х3
= 0,269,
х4
= 0,327.
2. Численные методы аппроксимации и интерполяции функций
2.1 Задание
Найти интерполяционный полином второго порядка

методом неопределённых коэффициентов, используя данные нулевого, второго и четвёртого опытов.
Найти аппроксимирующий полином первого порядка
 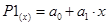
методом наименьших квадратов.
Исходные данные
0 1 2 3 4
| xi
|
0,1 |
0,3 |
0,5 |
0,8 |
1 |
| yi
|
0,3 |
0,55 |
0,65 |
0,4 |
0,25 |
2.2 Метод неопределенных коэффициентов
Метод неопределённых коэффициентов реализуется подстановкой полинома 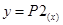 в систему: в систему:

где 0, 2, 4 номера заданных точек.
Подставим значения неизвестных из таблицы в систему:
 (2.1.1.) (2.1.1.)
Решим полученную систему методом Гаусса.
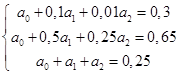 (2.1.2.) (2.1.2.)
Прямой ход
Все уравнения системы являются нормированными, поэтому сразу вычтем из второго и третьего уравнения первое, чтобы исключить из системы а0
.
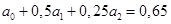
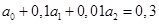 (2.1.3.)
(2.1.3.)

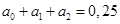
 (2.1.4.)
(2.1.4.)

В итоге получаем систему уравнений:
 (2.1.5.) (2.1.5.)
Рассмотрим систему (2.1.5.) без первого уравнения.
 (2.1.6.) (2.1.6.)
Нормируем первое уравнение системы (2.1.6.):
 (2.1.7.) (2.1.7.)
Умножим уравнение (2.1.7) на коэффициент при а1
второго уравнения системы (2.1.6.):
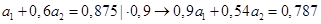 (2.1.8.) (2.1.8.)
Вычтем полученное уравнение (2.1.8.) из второго уравнения системы (2.1.6.), чтобы исключить из системы а1:

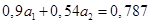 (2.1.9.)
(2.1.9.)

В результате получим эквивалентную систему линейных алгебраических уравнений
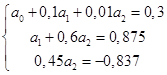 (2.1.10.) (2.1.10.)
Нормируем последнее уравнение системы (2.1.10.)
 (2.1.11.) (2.1.11.)
Получим систему, приведенную к треугольному виду.
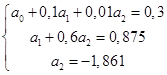 (2.1.12.) (2.1.12.)
Обратный ход
а2
= -1,861;
а1
= 0,875–0,6·(-1,861) = 1,992;
а0
= 0,3–0,01·(-1,861) – 0,1·1,992= 0,119
В итоге мы получаем интерполяционный полином второго порядка:
у =  = -1,861 х2
+1,992 х+0,119 = -1,861 х2
+1,992 х+0,119
Построим график интерполяционного полинома. Для этого вычислим его значения в определенных точках.
| xi
|
0,2 |
0,3 |
0,4 |
0,6 |
0,7 |
0,8 |
0,9 |
| yi
|
0,44 |
0,55 |
0,62 |
0,64 |
0,60 |
0,52 |
0,40 |
2.3 Метод наименьших квадратов
Метод наименьших квадратов реализуется с помощью, так называемой системы нормальных уравнений, имеющих матричный вид:

 = 2,7 = 2,7
 = 1,99 = 1,99
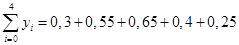 = 2,15 = 2,15


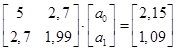
Выполним умножение матриц. Система нормальных уравнений примет вид:
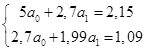 (2.2.1) (2.2.1)
Решим систему методом Гаусса.
Прямой ход
Нормируем первое уравнение системы (2.2.1)
 (2.2.2) (2.2.2)
Умножим полученное уравнение (2.2.2) на коэффициент при а0
во втором уравнении
 (2.2.3) (2.2.3)
Вычтем уравнение (2.2.3) из второго уравнения системы (2.2.1), чтобы исключить а0
из системы.

 (2.2.4)
(2.2.4)
0,532а1
= -0,071
Получим новую систему уравнений:
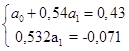 (2.2.5) (2.2.5)
Нормируем второе уравнение системы (2.2.5)
 (2.2.6) (2.2.6)
В результате получим систему линейных уравнений треугольного вида.
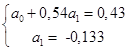 (2.2.7) (2.2.7)
Обратный ход:
а1
= -0,133
а0
= 0,43–0,54·(-0,133) = 0,502
Решив полученную систему, мы получили коэффициенты аппроксимирующего полинома первого порядка.
Полином будет иметь вид:
y = -0,133х+0,502
3. Численные методы решений нелинейных уравнений.
3.1 Исходные данные
| Уравнение
|
Отрезок
|
Шаг
|
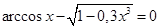 |
[0; 1] |
0,2 |
3.2 Отделение корней
Определим корни уравнения 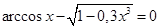 на отрезке [0; 1] с шагом 0,2 на отрезке [0; 1] с шагом 0,2
Подставим в функцию значение х, равное 0:

Подставим в функцию значение х, равное 0,2:
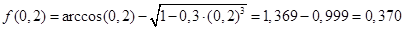
Подставим в функцию значение х, равное 0,4:

Подставим в функцию значение х, равное 0,6:

Подставим в функцию значение х, равное 0,8:
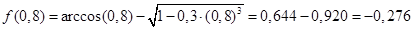
Подставим в функцию значение х, равное 1:
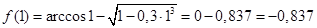
Из анализа полученных данных следует, что функция меняет знак на интервале [0,4; 0,6], следовательно, этот частичный интервал является интервалом изоляции корня, то есть на этом интервале существует корень, и при том единственный.
3.3 Уточнение корней методом половинного деления
Уточним корни уравнения с точностью ε  0,001 0,001
1)
Определим новое приближение корня к середине отрезка

Определим значение функции в точке с:

Выполним проверку |f(c)|  ε → |0,066| ε → |0,066|  0.001 – нет 0.001 – нет
Найдем интервал, в котором находится корень:
f(a)∙f(c) = f (0,4)∙ f (0,5) = (+)∙(+) = (+)
Смена знака не происходит, значит на этом интервале корня нет, следовательно корень находится на правой половине интервала изоляции корня.
Принимаем а = c = 0,5
В качестве нового приближения выбираем интервал [a; b] = [0,5; 0,6]
2)
Определим новое приближение корня к середине отрезка
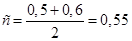
Определим значение функции в точке с:

Выполним проверку |f(c)|  ε → |0,013| ε → |0,013|  0.001 – нет 0.001 – нет
Найдем интервал, в котором находится корень:
f(a)∙f(c) = f (0,5)∙ f (0,55) = (+)∙(+) = (+)
Смена знака не происходит, значит на этом интервале корня нет, следовательно корень находится на правой половине интервала изоляции корня.
Принимаем a= c = 0,55
В качестве нового приближения выбираем интервал [a; b] = [0,55; 0,6]
3)
Определим новое приближение корня к середине отрезка

Определим значение функции в точке с:
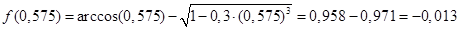
Выполним проверку |f(c)|  ε → |-0,013| ε → |-0,013|  0.001 – нет 0.001 – нет
Найдем интервал, в котором находится корень:
f(a)∙f(c) = f (0,55)∙ f (0,575) = (+)∙(–) = (–)
Смена знака произошла, следовательно, корень находится на левой половине интервала изоляции корня.
Принимаем b= c = 0,575
В ачестве нового приближения выбираем интервал [a; b] = [0,55; 0,575]
4)
Определим новое приближение корня к середине отрезка

Определим значение функции в точке с:

Выполним проверку |f(c)|  ε → |0,000| ε → |0,000|  0,001 – да. 0,001 – да.
Необходимое условие достигается на четвёртом приближении, где х = 0,563
Ответ: х = 0,563
3.4 Уточнение корней методом Ньютона
За начальное приближение принимается тот из концов отрезка [0,4; 0,6], на котором выполняется условие сходимости (смотри пункт 3.2).
Проверим условие сходимости в точке а = 0,4:






Проверим условие сходимости в точке b = 0,6:


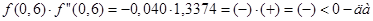
1)
За начальное приближение к корню принимаем значение х0
, равное 0,6
Вычислим первое приближение:


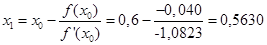
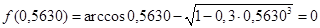
Погрешность вычисления:
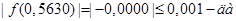
Приближенное значение корня х = 0,563
Ответ: х = 0,563
3.5 Уточнение корней методом простых итераций
Приведем уравнение к каноническому виду.

За начальное приближение принимается тот из концов отрезка [0,4; 0,6], на котором выполняется условие сходимости (смотри пункт 3.2).
Проверим условие сходимости в точке а = 0,4:
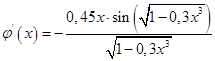
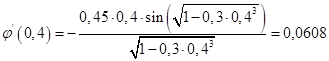
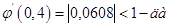
Примем за нулевое приближение
неизвестных значение 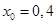
Выполним первую
итерацию
Найдем значение 

Выполним проверку:
|x1
-x0
| = |0,5484 – 0,4| = 0,1484 < 0,001 – нет
Выполним вторую
итерацию
Найдем значение 

Выполним проверку:
|x2
-x1
| = |0,5612 -0,5484| = 0,0128  0,001 – нет 0,001 – нет
Выполним третью
итерацию
Найдем значение 
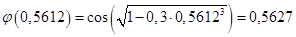
Выполним проверку:
|x3
-x2
| = |0,5627 – 0,5612 | = 0,0015  0,001 – нет 0,001 – нет
Выполним четвёртую
итерацию
Найдем значение 
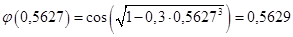
Выполним проверку:
|x1
-x0
| = |0,5629 – 0,5627| = 0,0002  0,001 – да 0,001 – да
Приближенное значение корня х = 0,5629
4. Численные методы вычисления определенных интегралов
4.1 Исходные данные
| Интеграл
|
Шаг
|
Точность
|
 |
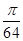 |
0,001 |
Вычислим интеграл по формуле Ньютона-Лейбница.

Вычислим значения подынтегральной функции в точках разбиения xi
, где i = 0,1,2..n.
 0 0 0,4142 0,4142
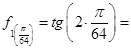 0,0985 0,0985 0,5345 0,5345
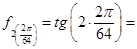 0,1989 0,1989 0,6682 0,6682
 0,3033 0,3033  0,8207 0,8207
 1 1
Результаты сведены в таблицу:
4.2 Вычислим интеграл методом левых прямоугольников
Iлп
= h·[f(x0
) + f(x1
) + f(x2
) + … + f(xn
-1
)] = 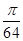 ·[0+0,0985+0,1989+0,3033+0,4142+0,5345+0,6682+0,8207] = 0,1491 ·[0+0,0985+0,1989+0,3033+0,4142+0,5345+0,6682+0,8207] = 0,1491
Ошибка вычисления:
О = |0,173–0,1491| = 0,0239  = 0,001 – нет. = 0,001 – нет.
4.3 Вычислим интеграл методом правых прямоугольников
Iпп
= h·[f(x1
) + f(x2
) + f(x3
) + … + f(xn
)] = 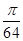 ·[0,0985+0,1989+0,3033+0,4142+0,5345+0,6682+0,8207+1] = 0,1982 ·[0,0985+0,1989+0,3033+0,4142+0,5345+0,6682+0,8207+1] = 0,1982
Ошибка вычисления:
О = |0,173–0,1982| = 0,0252  = 0,001 – нет. = 0,001 – нет.
4.4 Вычислим интеграл методом центральных прямоугольников
Вычислим значения подынтегральной функции в центре каждого выделенного интервала:
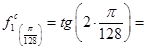 0,0491 0,0491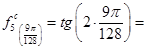 0,4730 0,4730
 0,1483 0,1483 0,5994 0,5994
 0,2505 0,2505 0,7416 0,7416
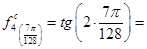 0,3578 0,3578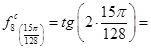 0,9063 0,9063
Результаты сведены в таблицу:
Iцп
= h·[f с
(x1
) + f с
(x2
) + f с
(x3
) + … + f с
(xn
)] = 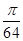 ·[0,0491+0,1483+0,2505+0,3578+0,4730+ ·[0,0491+0,1483+0,2505+0,3578+0,4730+
+0,5994+0,7416+0,9063] = 0,1731
Ошибка вычисления:
О = |0,173–0,1731| = 0,0001  = 0,001 – да. = 0,001 – да.
4.5 Вычислим интеграл методом трапеций
Iпп
= h·[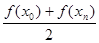 + f(x1
) + f(x2
) + … + f(xn-1
)] = + f(x1
) + f(x2
) + … + f(xn-1
)] = 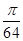 ·[ ·[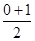 +0,0985+0,1989+0,3033+ +0,0985+0,1989+0,3033+
+0,4142+0,5345+0,6682+0,8207] = 0,1737
Ошибка вычисления:
О = |0,173–0,1737| = 0,0007  = 0,001 – да. = 0,001 – да.
4.6 Вычислим интеграл методом парабол
Iпп
= 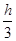 ·[f(x0
) + f(xn
) + 4·(f(x1
) + f(x3
) + … + f(xn
-1
)) + 2·(f(x2
) + f(x4
) + … + f(xn
-2
))] = ·[f(x0
) + f(xn
) + 4·(f(x1
) + f(x3
) + … + f(xn
-1
)) + 2·(f(x2
) + f(x4
) + … + f(xn
-2
))] =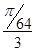 ·[0 +1 + 4·(0,0985+0,3033+0,5345+0,8207) + 2·(0,1989+0,4142+0,6682)] = 0,1733 ·[0 +1 + 4·(0,0985+0,3033+0,5345+0,8207) + 2·(0,1989+0,4142+0,6682)] = 0,1733
Ошибка вычисления:
О = |0,173–0,1733| = 0,0003  = 0,001 – да. = 0,001 – да.
5. Численные методы решений обыкновенных дифференциальных уравнений первого порядка
5.1 Исходные данные
| Уравнение
|
Начальные условия
|
Интервал
|
Шаг
|
 |
y(0) = 2,2 |
[0; 0,25] |
0,05 |
Решим дифференциальное уравнение первого порядка  в интервале [0; 0,25] с шагом 0,05 и начальными условиями y(0) = 2,2 в интервале [0; 0,25] с шагом 0,05 и начальными условиями y(0) = 2,2
5.2 Метод Эйлера
Запишем итерационные формулы метода Эйлера.


Вычислим значения функций при i
= 0
:

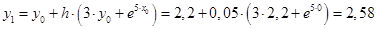
Вычислим значения функций при i
= 1
:

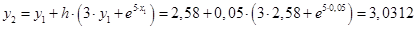
Вычислим значения функций при i
=2
:

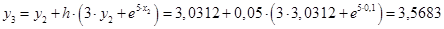
Вычислим значения функций при i
= 3
:
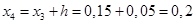

Вычислим значения функций при i
= 4
:
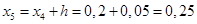

Результаты расчетов сведены в таблицу:
| i
|
x
i
|
y
i
|
| 0 |
0 |
2,2 |
| 1 |
0,05 |
2,58 |
| 2 |
0,10 |
3,0312 |
| 3 |
0,15 |
3,5683 |
| 4 |
0,20 |
4,2094 |
| 5 |
0,25 |
4,9767 |
5.3 Модифицированный метод Эйлера
Запишем итерационные формулы модифицированного метода Эйлера.
 
Вычислим значения функций при i
= 0
:

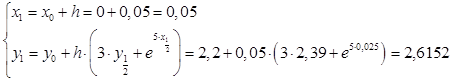
Вычислим значения функций при i
= 1
:
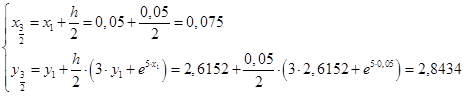
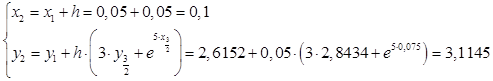
Вычислим значения функций при i
= 2
:
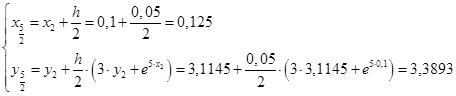
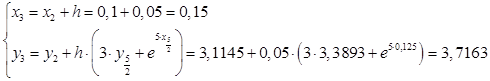
Вычислим значения функций при i
= 3
:


Вычислим значения функций при i
= 4
:

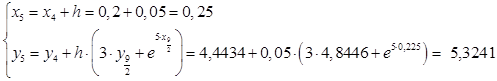
Результаты расчетов сведены в таблицу:
| №
|
x
i+1/2
|
y
i+1/2
|
x
i
|
y
i
|
| 0 |
0 |
2,2 |
| 1 |
0,025 |
2,3900 |
0,05 |
2,6152 |
| 2 |
0,075 |
2,8434 |
0,10 |
3,1145 |
| 3 |
0,1250 |
3,3893 |
0,15 |
3,7163 |
| 4 |
0,1750 |
4,0479 |
0,20 |
4,4434 |
| 5 |
0,2250 |
4,8446 |
0,25 |
5,3241 |
5
.
4
Усовершенствованный
метод
Эйлера
–
Коши
Запишем итерационные формулы улучшенного метода Эйлера – Коши.
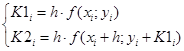

Вычислим значения коэффициентов и функций при i
= 0
:


Вычислим значения коэффициентов и функций при i
= 1
:

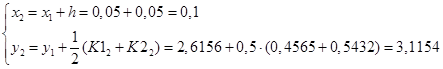
Вычислим значения коэффициентов и функций при i
= 2
:


Вычислим значения коэффициентов и функций при i
= 3
:
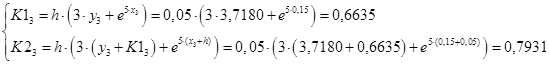
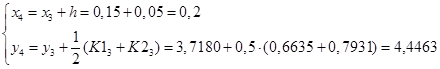
Вычислим значения коэффициентов и функций при i
= 4
:

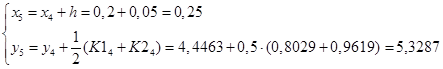
Результаты расчетов сведены в таблицу:
численный уравнение интерполяция интеграл
| №
|
К
1i
|
К
2i
|
x
i
|
y
i
|
| 0 |
0,38 |
0,4512 |
0 |
2,2 |
| 1 |
0,4565 |
0,5432 |
0,05 |
2,6156 |
| 2 |
0,5497 |
0,6556 |
0,1 |
3,1154 |
| 3 |
0,6635 |
0,7931 |
0,15 |
3,7180 |
| 4 |
0,0829 |
0,9619 |
0,2 |
4,4463 |
| 5 |
0,25 |
5,3287 |
|