Курсовая работа
Тема: "Типовой алгоритм синтеза комбинированной САУ"
Введение
Промышленные объекты управления (ОУ), как правило, представляют собой сложные агрегаты со многими входными и выходными величинами, характеризующими технологический процесс. Зависимости выходных величин от входных, как правило, нелинейные, и изменение одной из них приводит к изменению других. Таким образом, создается сложная система взаимозависимостей, которую трудно, а подчас и невозможно строго математически описать.
Большинство промышленных объектов описываются передаточными функциями, имеющими большое время запаздывания τа
и большие постоянные времени Та
.
Известно, что чем больше время запаздывания, тем труднее управлять объектом. Качество регулирования в будущей САУ зависит от отношения τа
/ Та
. Чем оно больше, тем труднее управлять, поэтому при описании объекта (τа
/ Та
)≤1.
Для большинства объектов τа
/ Та
так велико, что удовлетворяющее нас качество в системе в одноконтурной САУ получить практически невозможно. В этом случае нужно усложнить закон регулирования. На практике идут не на усложнение закона регулирования, а на усложнение структуры САУ.
В настоящее время в практике автоматизации непрерывных производственных процессов применяются следующие виды многоконтурных схем: каскадные системы, комбинированные САУ и многосвязные системы. Расчет оптимальных параметров управляющих устройств перечисленных многоконтурных систем является довольно сложной задачей. Для упрощения на практике определяют лишь приближенные значения этих параметров.
Методика приближенных расчетов основана на предположении о возможности расчета отдельных контуров системы независимо друг от друга. Для этих целей, исходная структурная схема управления подвергается различным структурным преобразованиям с тем, чтобы выделить отдельные контуры с различными частотами и рассчитывать их обычными методами независимо друг от друга, тем самым получают более сложный алгоритм управления комбинацией ограниченного числа типовых П -, ПИ-, ПИД законов регулирования.
Комбинированные системы регулирования рекомендуется строить, если на систему действуют значительные внешние возмущения и если представляется возможность выделить и измерить главные из них.
Система содержит минимум два контура регулирования. Разомкнутый контур с преобразователем  служит для компенсации основного возмущения (или возмущений) f; замкнутый контур с регулятором служит для компенсации основного возмущения (или возмущений) f; замкнутый контур с регулятором  окончательно корректирует процесс, отрабатывая ошибки компенсации первого контура и другие неучтенные возмущения, многие из которых практически не могут быть контролируемыми (помехи). Комбинированное управление сочетает в себе два принципа регулирования: регулирование «по возмущению» и регулирование «по отклонению». окончательно корректирует процесс, отрабатывая ошибки компенсации первого контура и другие неучтенные возмущения, многие из которых практически не могут быть контролируемыми (помехи). Комбинированное управление сочетает в себе два принципа регулирования: регулирование «по возмущению» и регулирование «по отклонению».
1.1 Аппроксимация переходной характеристики объекта по управляющему каналу
Экспериментальным точкам строится экспериментальная характеристика переходного процесса. Исследуемый объект – двухканальный (канал: u-y и канал: f-y) по каналу регулирования (u-y) является объектом с самовыравниванием (рис. 2). Объекты с самовыравниванием аппроксимируют передаточными функциями с введением звена запаздывания.

Рис. 2. Переходная характеристика ОУ с самовыравниванием
 , (1.1) , (1.1)
автоматический управление аппроксимация канал
где:
Коб
– коэффициент передачи;
t – время запаздывания;
То
– постоянная времени.
Простейшим частным случаем оператора (1.1), имеющим в инженерной практике наибольшее применение, является передаточная функция вида:
 . (1.2) . (1.2)
Для определения параметров объекта по управляющему каналу проведём касательную к экспериментальной переходной характеристике в точке перегиба, которая имеет координатами (tп
; h(tп
)). Далее определяем параметры передаточной функции по управляющему каналу (приложение 1):
Коб
= hуст
= 0,55; tо
= 1,9с; То
= 10,5с; h(tп
) = 0,12; tп
= 4с

Подставляя эти параметры в формулу (1.2), получаем первую математическую модель ОУ:
 
Более точную аппроксимацию переходной функции ОУ дает передаточная функция вида:
 (1.3) (1.3)
Её оригинал имеет вид:
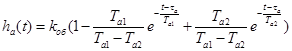 (1.4) (1.4)
Задача математического описания в этом случае заключается в поиске таких Та1
, Та2
и  , при которых кривая (1.4) максимально приближается к истинной экспериментальной кривой. Записывая аналитические выражения критерия приближения, получаем уравнения для выбора этих параметров. Для упрощения расчётов, в литературе предложена номограмма: , при которых кривая (1.4) максимально приближается к истинной экспериментальной кривой. Записывая аналитические выражения критерия приближения, получаем уравнения для выбора этих параметров. Для упрощения расчётов, в литературе предложена номограмма:

Рис. 3. Номограмма для определения параметров передаточных функций
По номограмме (рис. 3.) можно найти  , ,  по известным по известным  и и  . По известному значению . По известному значению  находим значение находим значение  , после чего определяем , после чего определяем  , , 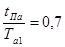 и, следовательно: и, следовательно:




Подставляя рассчитанные значения в формулу (1.3), получаем вторую математическую модель ОУ:

Третью модель определяем по методу Лукаса:
 , ,
где  ; ;

Таким образом, получили третью математическую модель ОУ:

Далее с помощью программы «СС» на ЭВМ строим переходные процессы полученных функций и наносим их на график с экспериментальной характеристикой (приложение 1).
Вычислим погрешности аппроксимации полученных передаточных функций по интегральному критерию по формуле:
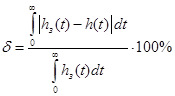
где:
 - аппроксимирующая переходная характеристика; - аппроксимирующая переходная характеристика;
 - заданная переходная характеристика. - заданная переходная характеристика.

Выбираем передаточную функцию, имеющую наименьшую погрешность аппроксимации:
 (1.5)
(1.5)
Исследуемый объект по возмущающему каналу также является объектом с самовыравниванием (рис. 2.). Поэтому первая аппроксимирующая передаточная функция примет форму оператора (1.1).
Проведём касательную к экспериментальной переходной характеристике в точке перегиба с координатами (tп
; h(tп
)) (приложение 2.). Определим параметры передаточной функции:
Коб
= hуст
= 0,28; tо
= 3,1с; То
= 9с; h(tп
) = 0,06; tп
= 5с

Получили передаточную функцию первой модели для возмущающего канала:

Далее для нахождения передаточной функции второй модели (1.3) как и в предыдущем пункте по номограмме (рис. 3) находим:




Подставляя рассчитанные значения в формулу (1.3), получаем вторую математическую модель ОУ:

Для нахождения передаточной функции по методу Лукаса определяем следующие коэффициенты:
 ; ;

Таким образом, получили третью передаточную функцию для возмущающего канала:

Находим погрешности аппроксимации по интегральному критерию:
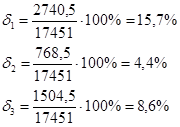
Выше представленные расчёты показывают, что наименьшую погрешность аппроксимации даёт третья модель, следовательно, она наилучшим образом аппроксимирует экспериментальную характеристику.

2. Выбор ПИ-алгоритма управления
В качестве показателя оптимальности АСР принимается минимум интеграла от квадрата ошибки системы при действии на объект наиболее тяжелого ступенчатого возмущения по регулирующему каналу (интегральный квадратичный критерий) с учетом добавочного ограничения на запас устойчивости системы, т.е.
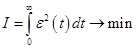 . (2.1) . (2.1)
Такой критерий допускает значительное перерегулирование  и увеличивает время регулирования, но он обеспечивает наименьшее максимальное динамическое отклонение регулируемой величины. и увеличивает время регулирования, но он обеспечивает наименьшее максимальное динамическое отклонение регулируемой величины.
При практических расчётах запас устойчивости удобно характеризовать показателем колебательность системы М, значение которого в САУ, имеющих интеграл в алгоритме управления, совпадает с максимумом амплитудно-частотной характеристики системы:
 (2.2) (2.2)
где:
wр
– резонансная частота, на которой Аз
() имеет максимум.
Чтобы максимум не превышал некоторой заданной величины М, амплитудно-фазовая характеристика (АФХ) разомкнутой системы Wраз
(j) не должна заходить внутрь «запретной» области ограниченной окружностью, центр uo
и радиус Ro
которой определяется через М формулами (2.3) и (2.4), (рис. 4):
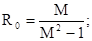 (2.3) (2.3)
 . (2.4) . (2.4)

Рис. 4. Определение центра и радиуса окружности, соответствующей заданному показателю колебательности М
Если же Wраз
(j) касается указанной окружности, то это означает, что САУ находится на границе заданного запаса устойчивости.
На практике чаще всего принимают  . При этом в САУ перерегулирование g £ 30%, максимальное отклонение регулируемого параметра при внутренних возмущениях (возмущениях по регулирующему воздействию) не превышает 10%. . При этом в САУ перерегулирование g £ 30%, максимальное отклонение регулируемого параметра при внутренних возмущениях (возмущениях по регулирующему воздействию) не превышает 10%.
С помощью программы «СС» рассчитываем и строим АФХ объекта по передаточной функции (1.5) (приложение 3). Результаты расчёта приведены в таблице 2:
Таблица 2
| 
|
0
|
0,042
|
0,082
|
0,131
|
0,192
|
0,255
|
0,339
|
0,451
|
0,599
|
0,797
|
| А
|
0,55
|
0,536
|
0,5
|
0,44
|
35
|
0,279
|
0,2
|
0,136
|
0,086
|
0,052
|
| 
|
0
|
-20
|
-38,7
|
-60
|
-81,7
|
-100,6
|
-120,5
|
-140,4
|
-160
|
-179,6
|
| 
|
0,797
|
1,06
|
1,409
|
2,059
|
3,009
|
| А
|
0,052
|
0,031
|
0,018
|
0,009
|
0,004
|
| 
|
-179,6
|
-199,7
|
-222
|
-256,9
|
-300,7
|
Также по передаточной функции (1.5) находим АЧХ, ФЧХ и  , которые находятся по комплексному коэффициенту усиления (2.5), который получается из передаточной функции путем замены р на , которые находятся по комплексному коэффициенту усиления (2.5), который получается из передаточной функции путем замены р на  . .

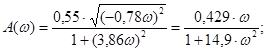 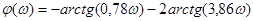

3. Расчет параметров ПИ-регулятора по параметрам объекта по регулирующему каналу графоаналитическим методом
Рассчитаем ПИ-алгоритм управления, передаточная функция которого имеет вид:
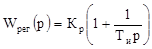 , (3.1) , (3.1)
а параметрами, подлежащими определению, являются коэффициент усиления Кр
и постоянная интегрирования Ти
, для этого используем графоаналитический метод.
1. По АФХ объекта Wоб
u-y
(jω) строим семейство характеристик разомкнутой системы Wраз
(jω) для Кр
= 1 и нескольких фиксированных значений постоянной интегрирования Ти
.
Для этого сначала строим несколько векторов характеристики объекта Wоб
u-y
(jω), например, векторы  для частоты ω1
, для частоты ω1
, 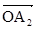 для ω2
и т.д. (приложение 3). К их концам надо пристроить векторы для ω2
и т.д. (приложение 3). К их концам надо пристроить векторы  , , 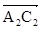 ,…, ,…,  , повернутые по отношению к векторам , повернутые по отношению к векторам  , , 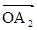 ,…, ,…,  на угол 90°. Длина векторов на угол 90°. Длина векторов  , ,  ,…, ,…, 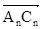 выбирается из соотношения выбирается из соотношения  (где в числителе (где в числителе  – длина вектора АФХ объекта для определённого значения частоты wi
, которую можно измерить непосредственно в миллиметрах; в знаменателе – произведение указанной частоты на фиксированное значение Ти
). Через полученные точки С1
, С2
,…, Сn
проводим плавную кривую, которая является характеристикой Wраз1
(jω) для выбранного значения Ти
. – длина вектора АФХ объекта для определённого значения частоты wi
, которую можно измерить непосредственно в миллиметрах; в знаменателе – произведение указанной частоты на фиксированное значение Ти
). Через полученные точки С1
, С2
,…, Сn
проводим плавную кривую, которая является характеристикой Wраз1
(jω) для выбранного значения Ти
.
Через полученные точки С1
, С2
,…, Сn
проводим плавную кривую, которая является характеристикой Wраз1
(jω) для выбранного значения Ти
.
Аналогичные построения проводим для других значений Ти
. В итоге получаем семейство характеристик Wраз
(jω) для различных значений Ти
.
2. Из начала координат проводим прямую ОЕ под углом b, характеризующим запас устойчивости по фазе и определяемым как:
 . (3.2) . (3.2)
3. С помощью циркуля вычерчиваем окружности с центром на отрицательной вещественной полуоси, каждая из которых касается одновременно как прямой ОЕ, так и одной из характеристик Wраз1
(jω) (центр каждой окружности и ее радиус находим подбором).
4. Отношение требуемого радиуса R0
, определяемого по формуле (2.3), к полученному в каждом отдельном случае значению ri
показывает, во сколько раз нужно изменить единичный коэффициент передачи регулятора (Кр
=1), чтобы каждая характеристика Wраз1
(jω) касалась окружности с заданным М, т.е.
 . (3.3) . (3.3)
Для вычисления Кр. пред
использована формула:
 , (3.4) , (3.4)
где:
Rо
– радиус, определяемый по формуле (2.3);
r – радиус окружности, находящийся методом подбора;
Все результаты вычислений представлены в таблице 3:
Таблица 3
| Кр
|
2,44
|
3,2
|
4,1
|
4,8
|
| Ти
|
4
|
5
|
6
|
8
|
5. В результате в плоскости варьируемых параметров алгоритма Кр
и Ти
строится граница области заданного запаса устойчивости (приложение 3).
Максимум отношения Кр
/Ти
, определяющего оптимальную настройку регулятора при низкочастотных возмущениях, соответствует точке пересечения касательной с границей заданного запаса устойчивости, проведённой через начало координат.
Передаточная функция регулятора, после определения координат точки А (Кр.опт
= 4,5 и Ти опт
= 6,55), имеет вид:
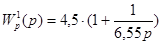
4.
Расчет параметров ПИ-регулятора частотным методом на ЭВМ
В основу метода положено представление о том, что минимум интеграла от квадратичной ошибки при единичной ступени по управляющему каналу соответствуют оптимальные параметры ПИ-алгоритма [5], отвечающего условиям:


При расчете оптимальных параметров  и и  используются следующие формулы: используются следующие формулы:
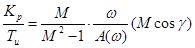 , (4.1) , (4.1)
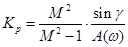 . (4.2) . (4.2)
 –
коэффициент усиления по амплитуде объекта, –
коэффициент усиления по амплитуде объекта,
 – угол, заключенный между вектором АФХ объекта и отрицательной мнимой полуосью. – угол, заключенный между вектором АФХ объекта и отрицательной мнимой полуосью.
Вычисление требуемых значений  и и  сводится к поиску такого значения сводится к поиску такого значения  , при котором , при котором  , ,  . .
 . .
Расчет параметров регулятора выполняем на ПЭВМ.
С помощью прикладного пакета программ «СС» по АФХ объекта управления по регулирующему каналу определяем частоты  и и  : :
 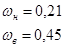
Далее в программе «Reguls» определяем коэффициент усиления и постоянную времени для регулятора:

Получаем регулятор:

5. Построение переходных процессов в системе по задающему воздействию при двух вариантах настройки регулятора
В соответствии с заданием для проверки правильности выполненных расчётов нужно построить переходные процессы в САУ по задающему воздействию. Расчет переходных характеристик проведем на ПЭВМ частотным методом, суть которого приведена ниже.
На первом этапе по заданной на ЭВМ передаточной функции замкнутой системы Wз
(р) рассчитывается вещественная частотная характеристика замкнутой системы. Для этого в выражение Wз
(р) подставляют  и, меняя частоту w от 0 до ¥, вычисляют вещественную часть и, меняя частоту w от 0 до ¥, вычисляют вещественную часть  : :
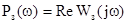 при w = 0; w1
; w2
, …, wmax
. (5.1) при w = 0; w1
; w2
, …, wmax
. (5.1)
Поскольку практически невозможно вычислить (5.1) для всего диапазона частот от 0 до ¥, приходится ограничиться некоторой максимальной частотой wmax
, которая выбирается таким образом, чтобы при w > wmax
вещественная частотная характеристика принимала пренебрежимо малые значения, например менее 5% от начального значения Рз
(0).
Второй этап расчёта заключается в получении переходного процесса по найденной на первом этапе Рз
(w) в диапазоне 0 £ w £ wmax
. Для этого используется известное выражение:
 при t > 0. (5.2) при t > 0. (5.2)
Интеграл (5.2) вычисляется приближённым (численным) методом для ряда значений времени t: от t = 0 до t = tmax
. Максимальное значение времени tmax
выбирают таким образом, чтобы к моменту t = tmax
переходный процесс y(t) практически закончился.
Из двух найденных регуляторов необходимо выбрать тот, который обеспечивает системе наилучшие показатели качества, для этого необходимо рассчитать и построить переходные процессы в системе по задающему воздействию. Запишем передаточную функцию системы по заданию:

Расчет и построение необходимых процессов производится в программе «СС». Переходный процесс в системе по задающему воздействию при настройках регулятора, найденных графоаналитически (приложение 3), представлен в приложении 4, рис. а), а при настройках регулятора, найденных на ЭВМ – в приложении 4, рис. б).
Определим показатели качества системы при настройках регулятора, найденных графоаналитическим методом (приложение. 4, рис. а):
1. Установившееся рассогласование (статическая ошибка):
 . .
2. Время регулирования:

3. Максимальное перерегулирование:

4. Колебательность:

5. Степень затухания:

При настройках регулятора, найденных частотным методом на ЭВМ (приложение 4, рис. б):
1. Статическая ошибка:
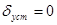
2. Время регулирования:

3. Перерегулирование:

4. Колебательность:

5. Степень затухания:

Сравнив полученные значения, можно сделать вывод о том, что регулятор, вычисленный частотным методом на ЭВМ, является более подходящим, т. к. он обеспечивает системе наилучшие показатели качества – система более устойчивая
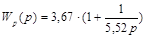
6. Получение передаточной функции физически реализуемого компенсатора, обеспечивающего наилучшую компенсацию возмущения
Одной из главных целей синтеза автоматической системы является обеспечение требуемой точности в установившихся и переходных режимах. Точность систем в установившихся режимах можно улучшить, увеличивая порядок астатизма и коэффициент разомкнутого контура. Но при этом, как правило, уменьшается запас устойчивости, увеличивается колебательность и, как следствие, ухудшается точность системы в переходных процессах. Эффективным средством устранения противоречия между условиями точности в установившихся и переходных режимах служит компенсация внешних воздействий путём осуществления инвариантности (независимости одной физической величины от другой).
Инвариантность в автоматических системах достигается при помощи управления по возмущению: управляющее воздействие формируется в зависимости от изменений возмущающего воздействия.
Рассмотрим схему комбинированной системы (рис. 1). Уравнение такой системы имеет вид:
  + + , (6.1) , (6.1)
где:
 – передаточная функция системы по задающему воздействию; – передаточная функция системы по задающему воздействию;
 – передаточная функция системы по возмущению. – передаточная функция системы по возмущению.
Управляемая величина не зависит от возмущения, если передаточная функция по возмущению равна нулю. А это возможно, если равен нулю её числитель. Отсюда условие инвариантности стабилизируемой величины по отношению к возмущению:
 . .
Находим передаточную функцию компенсирующего устройства:
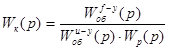 . (6.2) . (6.2)
Подставляя в формулу (6.2) найденные ранее передаточные функции объекта по различным каналам и регулятора, получаем передаточную функцию компенсирующего устройства:

где запаздывание можно разложить следующим образом:

 (6.3) (6.3)
Для удобства практической реализации компенсатора используется типовой физически реализуемый компенсатор, передаточная функция которого имеет вид:
 (6.4) (6.4)
Вопрос при этом сводится к поиску таких k1
и Тк
, при которых выражение (6.4) максимально приближается к (6.3). Делается это по следующим формулам:
 , ,
где k – коэффициент усиления в формуле (6.3)
Ти – постоянная времени регулятора
По формулам разложения дробно-рациональных функций:

Полученная передаточная функция физически реализуемого компенсатора имеет вид:

7. Определение показателей качества в системе по возмущающему воздействию
Для построения переходной характеристики по возмущающему воздействию запишем передаточную функцию по возмущению:
 
Расчет и построение данного переходного процесса выполняется в программе «СС», он показан в приложении 4, рис. в.
Определяем показатели качества системы:
1. Статическая ошибка:
 . .
2. Время регулирования:

3. Перерегулирование:

Качество управления считается удовлетворительным, если перерегулирование не превышает 30–40%.
4. Колебательность:
 . .
5. Степень затухания:

Интенсивность затухания колебаний в системе считается удовлетворительной, если  . .
Вывод:
Оценив переходные процессы по возмущающему воздействию, можно сделать вывод, что построенная система автоматического управления является работоспособной и имеет показатели качества на хорошем уровне.
8. Составление структурной схемы САУ с НЦУ и запись алгоритма цифрового управления
Одним из ценнейших функциональных преимуществ НЦУ является возможность точной реализации алгоритмов управления любой сложности. Однако в настоящее время большинство систем НЦУ являются цифровыми копиями традиционных аналоговых систем, поэтому все реальные системы НЦУ базируются на применении классических ПИ- и ПИД-алгоритмов управления.
Система автоматического регулирования с НЦУ (рис. 5) содержит объект управления и автоматический регулятор (очерчен штриховой линией). Роль последнего выполняет ЭВМ снабжённая рядом устройств, для преобразования сигналов из аналоговой формы в цифровую (АЦП), а также из цифровой формы в аналоговую (ЦАП). На рисунке 5 аналоговые сигналы обозначены как функции времени y(t), g(t), z(t). Соответствующие цифровые сигналы отличаются от них не только формой представления величин, но и дискретным характером изменения во времени. Изменения значений цифровых сигналов производится в моменты времени  где Тд
– интервал дискретности; i = 0, 1, 2, … где Тд
– интервал дискретности; i = 0, 1, 2, …
Цифровые сигналы обозначены на схеме как переменные с индексами y[n], g[n], z[n], причём y[n] = y(nTд
); g[n] = g(nТд
); z[n] = z(nТд
). Интервал дискретности Тд
выбирается из условия: Тд
£Ти
.
0,1, где Ти
– постоянная времени интегрирования непрерывного регулятора. В нашем случае: Тд
= 5,52/10 = 0,552 с.
 Рис. 5. Структурная схема системы НЦУ Рис. 5. Структурная схема системы НЦУ
Алгоритм работы ЭВМ, осуществляющий автоматическое регулирование, может быть получен из уже найденного закона регулирования непрерывного регулятора.
Принимаем за исходный ПИ-закон:
 (8.1) (8.1)
где:
u1
(t) – регулирующее воздействие на объект;
e(t) – сигнал ошибки,
e(t) = g(t) – y(t); Кр
и Ти
– параметры настройки непрерывного ПИ-регулятора.
Замена непрерывных сигналов цифровыми, взятыми в дискретные моменты, может быть проведена по следующей схеме:
e(t) ® e[n]; u1
(t) ® u1
[n]; 
Здесь и ниже для удобства записи принимаем:
u[nT0
]=u[n]; 
ПИ-закон регулирования в цифровой форме имеет вид:
 (8.2) (8.2)
Более удобна для реализации на ЭВМ другая, так называемая скоростная форма этого алгоритма. Для её получения запишем значение u1
на предыдущем интервале дискретности:
 
Вычитая его из предыдущего, получим:

Отсюда:

После подстановки e[n] = g[n] – y[n]; e[n-1] = g[n] – y [n-1] получим:

Подставив значения всех постоянных коэффициентов, получим:
 (8.3) (8.3)
Алгоритм работы ЭВМ, осуществляющий компенсацию возмущающего воздействия, может быть получен на основании передаточной функции компенсатора следующим образом.
Пусть, например, сигнал компенсатора u2
(t) подаётся на вход объекта (вместе с сигналом регулирования u1
) и пусть передаточная функция компенсатора:
 . (8.4) . (8.4)
Тогда соответствующее операторное выражение имеет вид:

и в дифференциальной форме записывается в виде:

Переход к цифровым сигналам, взятым в дискретные моменты времени, может быть проведён по следующей схеме:
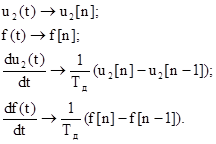
В результате перехода получим:

Отсюда:
 . .
Подставив значения всех постоянных коэффициентов, получим:

 
 (8.5) (8.5)
Окончательно управляющее воздействие цифрового регулятора с компенсацией возмущений получают суммированием регулирующего u1
(t) и компенсирующего u2
(t) воздействий:
 (8.6) (8.6)
 (8.7) (8.7)
9. Построение САУ с использованием методов нечёткой логики
Необходимо построить САУ с использованием методов нечёткой логики (фаззи-логики), оставив регулятор Р чётким, а компенсатор К выполнить нечётким.
Традиционный подход к синтезу САУ основывается на том, что модель ОУ заранее известна и задана либо в виде экспериментальных переходных характеристик, либо в виде передаточных функций отдельных каналов объекта. При известной цели управления алгоритм функционирования управляющего устройства (УУ) в этом случае однозначно предопределяется самой моделью и целью управления.
Однако на практике при автоматизации сложных технологических процессов, в том числе и процессов горно-обогатительного производства, получить математическую модель, достаточно полно отражающую реальные процессы в объекте, практически невозможно. Поэтому большинство реально действующих в промышленности автоматических систем управления сложными процессами создано, как правило, с использованием не только методов классической теории управления, но и с использованием методов экспериментального уточнения параметров системы, т.е. так называемой «настройкой системы на объект».
В настоящее время на смену этим методам приходят новые методы создания алгоритмов управления, выполненные на основе так называемой нечёткой логики (фаззи-логики).
9.1 Структурная схема комбинированной САУ с нечётким компенсатором
Необходимо составить структурную схему САУ с нечётким компенсатором, подав на него сигналы возмущения f и его производной f’
.
 На рисунке 6 представлена структурная схема комбинированной системы регулирования с Fuzzy-компенсатором: На рисунке 6 представлена структурная схема комбинированной системы регулирования с Fuzzy-компенсатором:
   
Рис. 7. Структурная схема САУ с Fuzzy-компенсатором
Fuzzy-компенсатор содержит три основных блока: F – блок фаззификации БФ, I – блок нечеткого вывода БНВ (блок принятия решений), D – блок дефаззификации БДФ.
Вся информация о стратегии управления заложена в базе знаний в виде правил условного логического вывода: Если…. тогда… Эти правила получаются за счет тщательного изучения ОУ и цели его управления путем анкетного опроса экспертов (технологи-операторы, специалисты по автоматизации).
Центральным звеном является БНВ, в котором нечеткая информация о возмущении f (его производной) формирует нечеткое множество управления.
Выполняется инференц-процедура, в результате которой объединяются выводы нечетких правил, и результатом этого объединения является усеченное множество управляющих воздействий.
БФ преобразует конкретное измеренное значение возмущения с помощью некоторой функции принадлежности в нечеткое множество. В БДФ происходит обратный процесс.
9.2 Расчёт управляющего воздействия нечёткого компенсатора
Необходимо рассчитать компенсирующее воздействие нечёткого компенсатора u2
для случая, когда |f| = 0,2 и |f’
| = 0,1. Упрощённый алгоритм нечёткого управления представлен следующими двумя правилами:
Правило №1: Если |f| = ПБ ИЛИ |f’
| = ПН, тогда Uк
= ПБ;
Правило №2: Если |f| = ОБ И |f’
| = ПН, тогда Uк
= ПН.
Fuzzy-логика осуществляется в 3 этапа:
I
этап – фаззификация
.
Фаззификация осуществляет переход от четких измеренных значений f и f’ к нечеткому множеству значений входа. Этот переход осуществляется с помощью функций принадлежности. Каждому значению f ставится в соответствие определенное значение функции принадлежности. После этого начинается II
этап – разработке нечетких правил.
Вычисление этих правил состоит из двух процедур: сначала рассчитывается все в части Если, а потом в части Тогда.
Посылка «ЕСЛИ», первого правила, содержащая внутри себя союз «ИЛИ» даёт значение функции принадлежности m1
(f1
, f2
), соответствующее логической конъюнкции:
m1
(f, f’
) = max{mПБ
(f), mПН
(f’
)} = max {0,4; 0,8} = 0,8;
m2
(f, f) = min{mОБ
(f), mПН
(f’
)} = min {0,4; 0,2} = 0,2.
Теперь в соответствии с композиционным правилом Мамдани:
mj
n
(x, uj
) = min{mj
(x), m1
(uj
)} (6.1)
где mj
n
(x, uj
) – ФП, характеризующая i – лингвистическое значение управляющего воздействия u в j – правиле;
x – вектор входных переменных.
Можно определить результирующие функции принадлежности, характеризующие импликации правил 1 и 2 (приложение 5.), где mi
U
2
– функции принадлежности, характеризующие фаззи-множества управляющих воздействий u. Так как функции m1,2
(f1
, f2
) принимают конкретные значения, меньшие единицы, то результатам импликации соответствуют «усечённые» функции принадлежности mi
U
2
(приложение5).
Выполняя процедуру фаззи-объединения функций mi
U
2
(агрегирование) получаем результирующую функцию принадлежности m*
(U2
) (приложение 5).
Заключительным этапом Fuzzy-логики является дефаззификация
, которая сводится к определению точного значения управляющего воздействия u
по нечеткому множеству. Она выполняется чаще всего по методу центра тяжести, согласно которому для непрерывной функции искомое значение управляющего воздействия определяется как абсцисса центра тяжести площади фигуры, образованной этой функцией и осью u.
 . .
На практике широко используется упрощённая формула, в которой интеграл заменяется суммой, т.е.

где ui
– абсцисса среднего (центрального) значения выходного множества (управляющих воздействий);
mpi
(u) – функция принадлежности – высота отсечения – выходного множества (управляющих воздействий).
Заключение
В данной работе выполнен синтез комбинированной САУ техническим объектом, заданным в форме экспериментальных переходных характеристик. Произведен выбор математической модели объекта управления в форме передаточных функций по управляющему и возмущающему каналам, выбран ПИ алгоритм управления и произведен расчет параметров ПИ-регулятора графоаналитическим методом. Рассчитан физически реализуемый компенсатор, обеспечивающий компенсацию возмущений. Построены кривые переходных процессов в системе и определены показатели качества. Осуществлен переход од аналогового (непрерывного) регулятора к НЦУ. Построена САУ с использованием методов нечёткой логики. Рассчитано компенсирующее воздействие нечёткого компенсатора.
Список используемой литературы
1. Теория автоматического управления. Расчёт САУ горного производства с использованием ЭВМ: Метод, указания для студентов спец. 2105 / ЛГИ Сост.: В.И. Златкин, С.В. Стороженко. Л., 1991 г. 46 с.
2. Лукас В.А. Основы теории автоматического управления. Л.: Недра, 1977 г. 376 с.
3. Медведев Р.Б., Бондарь Ю.Д., Романенко В.Д. АСУ в металлургии. М.: Металлургия, 1987 г. 253 с.
4. Марюта А.Н., Качан Ю.Г., Бунько В.А. Автоматическое управление технологическими процессами обогатительных фабрик. М.: Недра, 1983 г. 248 с.
5. Теория автоматического управления: Программа, методические указания, контрольные задания и задания к курсовой работе / ЛГИ Сост.: В.И. Златкин, С.В. Стороженко. СПб, 1992 г. 40 с.
|