СОДЕРЖАНИЕ
планирование эксперимент модель
ВВЕДЕНИЕ
1 Общие сведения о планировании эксперимента
2 Краткая характеристика методики составления планов эксперимента для моделей первого и второго порядков
2.1 Общие положения о планировании второго порядка
2.2 Ортогональные центральные композиционные планы второго порядка
2.3 Рототабельные планы второго порядка
ЗАКЛЮЧЕНИЕ
Список использованных источников
Развитие современной науки и техники связано с созданием новых и постоянным совершенствованием существующих научных и технологических процессов. Основой их разработки и оптимизации является эксперимент. Заметное повышение эффективности экспериментальных исследований и инженерных разработок достигается использованием математических методов планирования экспериментов. В процессе экспериментирования и при обработке полученных данных существенно сокращает сроки решения, снижает затраты на исследования и повышает качество полученных результатов.
Цель планирования эксперимента – нахождение таких условий и правил проведения опытов при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности.
Инициатором применения планирования эксперимента является Рональд А. Фишер, другой автор известных первых работ – Френк Йетс. Далее идеи планирования эксперимента формировались в трудах Дж. Бокса, Дж. Кифера. В нашей стране - в трудах Г.К. Круга, Е.В. Маркова и др.
Часто, приступая к изучению какого-либо процесса экспериментатор не имеет исчерпывающих сведений о механизме процесса. Можно только указать параметры определяющие условия протекания процесса, и, возможно требования к его результатам. Поставленная проблема является задачей кибернетики. Действительно, если считать кибернетику «наукой, изучающей системы любой природы, способные воспринимать, хранить и перерабатывать информацию для целей оптимального управления» [3], то такую систему можно представить в виде черного ящика.
Черный ящик – объект исследования, имеющий (k + p) входов и m выходов.

Зависимость между выходными параметрами (откликом) и входными параметрами (факторами) называется функцией отклика. Математическая запись функции отклика представлена в виде формулы (1):
 (1) (1)
Этому уравнению в многомерном пространстве соответствует гиперповерхность, которая называется поверхностью отклика, а само пространство – факторным пространством.
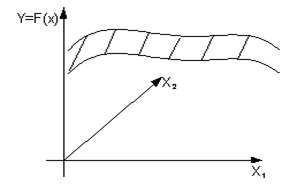
Рисунок 2 – Поверхность отклика
Для математического описания поверхности отдыха используют уравнение:
 (2) (2)
где 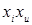 - перемешнные факторы при i=1,…,k; u=1,…,k; i - перемешнные факторы при i=1,…,k; u=1,…,k; i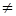 u; u;


 . .
Это уравнение является разложением в ряд Тейлора неизвестной функции отклика в окрестности точки с 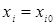 . .
На практике по результатам эксперимента производится обработка дан\ных по методу наименьших квадратов. Этот метод позволяет найти оценку b коэффициентов  , и данный полином заменяется уравнением вида: , и данный полином заменяется уравнением вида:
 (3) (3)
которое является регрессионной моделью (моделью регрессионного анализа). В этом выражении 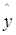 означает модельное, т.е. рассчитываемое по уравнению модели, значение выхода. Коэффициенты регрессии определяются экспериментально и служат для статистической оценки теоретических коэффициентов, т.е. означает модельное, т.е. рассчитываемое по уравнению модели, значение выхода. Коэффициенты регрессии определяются экспериментально и служат для статистической оценки теоретических коэффициентов, т.е.
 (4) (4)
В регрессионной модели члены второй степени 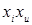 , , 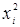  характеризуют кривизну поверхности отклика. Чем больше кривизна этой поверхности, тем больше в модели регрессии членов высшей степени. На практике чаще всего стремятся ограничиться линейной моделью [1]. характеризуют кривизну поверхности отклика. Чем больше кривизна этой поверхности, тем больше в модели регрессии членов высшей степени. На практике чаще всего стремятся ограничиться линейной моделью [1].
Эксперимент можно проводить по-разному. В случае, когда исследователь наблюдает за каким-то неуправляемым процессом, не вмешиваясь в него, или выбирает экспериментальные точки интуитивно, на основании каких-то привходящих обстоятельств, эксперимент считают пассивным. В настоящее время пассивный эксперимент считается неэффективным.
Гораздо более продуктивно проводится эксперимент, когда исследователь применяет статистические методы на всех этапах исследования, и, прежде всего, перед постановкой опытов, разрабатывая схему эксперимента, а также в процессе экспериментирования, при обработке результатов и после эксперимента, принимая решение о дальнейших действиях. Такой эксперимент считают активным, и он предполагает планирование эксперимента.
Под планированием эксперимента понимают процедуру выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.
Под математической моделью планирования понимается наука о способах составления экономических экспериментальных данных планов, которые позволяют извлекать наибольшее количество информации об объекте исследования, о способах проведения эксперимента, о способах обработки данных и их использование для оптимизации производственных процессов, а также инженерных расчетов [3].
Использование теории планирования эксперимента является одним из путей существенного повышения эффективности многофакторных экспериментальных исследований. В планировании экспериментов применяются в основном планы первого и второго порядков. Планы более высоких порядков используются в инженерной практике редко. В связи с этим далее приводится краткое изложение методики составления планов эксперимента для моделей первого и второго порядков. Под планом первого порядка понимают такие планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащего только первые степени факторов и их произведения:
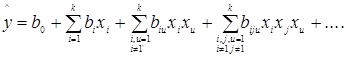 (5) (5)
Планы второго порядка позволяют провести эксперимент для отыскания уравнения регрессии, содержащего и вторые степени факторов:
 (6) (6)
Нахождение уравнения регрессии методом планирования экспериментов состоит из следующих этапов:
· выбор основных факторов и их уравнений;
· планирование и проведение собственного эксперимента;
· определение коэффициентов уравнения регрессии;
· статистический анализ результатов эксперимента [1].
2.1 Общие положения о планировании второго порядка
Описание поверхности отклика полиномами первого порядка часто оказывается недостаточным. Во многих случаях удовлетворительная аппроксимация может быть достигнута, если воспользоваться полиномом второго порядка (6).
В этом случае требуется, чтобы каждый фактор варьировался не менее чем на трех уровнях. В этом случае полный факторный эксперимент содержит слишком большое количество опытов, равное 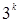 . Так, при . Так, при 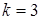 их 27, а число коэффициентов их 27, а число коэффициентов 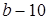 , при , при 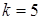 число опытов 243, а коэффициентов 21. В связи с этим осуществление полного факторного эксперимента (ПФЭ) для планов второго порядка не только сложно, но и нецелесообразно. число опытов 243, а коэффициентов 21. В связи с этим осуществление полного факторного эксперимента (ПФЭ) для планов второго порядка не только сложно, но и нецелесообразно.
Сократить число опытов можно, воспользовавшись так называемым композиционным или последовательным планом, разработанным Боксом и Уилсоном. Так, при двух факторах модель функции отклика 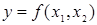 второго порядка представляет собой поверхность в виде цилиндра, конуса, эллипса и т.д., описываемую в общем виде уравнением: второго порядка представляет собой поверхность в виде цилиндра, конуса, эллипса и т.д., описываемую в общем виде уравнением:
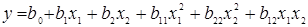 . (7) . (7)
Для определений такой поверхности необходимо располагать координатами не менее трех ее точек, т.е. факторы  и и 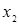 должны варьироваться не менее чем на трех уровнях. Поэтому план эксперимента в плоскости факторов должны варьироваться не менее чем на трех уровнях. Поэтому план эксперимента в плоскости факторов  и и 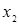 на рисунке 3, а не может состоять лишь из опытов 1, 2, 3, 4, располагающихся в вершинах квадрата, как это делается для модели первого порядка. К ним должны быть добавлены опыты (звездные точки) 5, 6, 7, 8, расположенные на осях на рисунке 3, а не может состоять лишь из опытов 1, 2, 3, 4, располагающихся в вершинах квадрата, как это делается для модели первого порядка. К ним должны быть добавлены опыты (звездные точки) 5, 6, 7, 8, расположенные на осях  и и 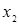 с координатами с координатами 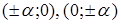 и обязательно опыт 9 в центре квадрата, чтобы по любому направлению (5-9-6), (1-9-4) и т.д. располагалось три точки, определяющие кривизну поверхности в этом направлении. и обязательно опыт 9 в центре квадрата, чтобы по любому направлению (5-9-6), (1-9-4) и т.д. располагалось три точки, определяющие кривизну поверхности в этом направлении.
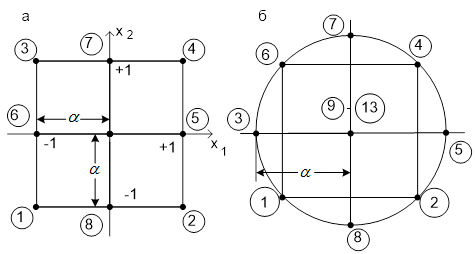
Рисунок 3 – Планы второго порядка при 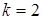 : а – ортогональный; : а – ортогональный;
б – рототабельный
Таким образом, в общем случае ядро композиционного плана составляет при  ПФЭ ПФЭ  , а при , а при 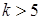 - дробную реплику от него. Если линейное уравнение регрессии оказалось неадекватным, необходимо: - дробную реплику от него. Если линейное уравнение регрессии оказалось неадекватным, необходимо:
1) добавить (2 – k) звездных точек, расположенных на координатных осях факторного пространства    где где  - звездное плечо, или расстояние до звездной точки; - звездное плечо, или расстояние до звездной точки;
2) провести 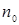 опытов при значениях факторов в центре плана. опытов при значениях факторов в центре плана.
При kфакторах общее число опытов в матрице композиционного плана составит:
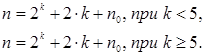 (8) (8)
При этом величина звездного плеча  и число опытов в центре плана и число опытов в центре плана 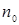 зависит от выбранного вида композиционного плана. зависит от выбранного вида композиционного плана.
Композиционный план для 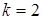 и и 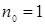 представлен в таблице 1. представлен в таблице 1.
Таблица 1 – Композиционный план второго порядка
| Номер опыта |
Факторы |
Результат |
 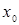 |
 |
 |
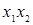 |
 |
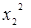 |
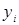 |
Ядро
плана
|
1
2
3
4
5
|
+1
+1
+1
+1
+1
|
- 1
+1
- 1
+1
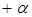
|
- 1
- 1
+1
+1
0
|
+1
- 1
- 1
+1
0
|
+1
+1
+1
+1

|
+1
+1
+1
+1
0
|
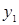


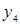

|
| Звездные точки |
6
7
8
|
+1
+1
+1
|
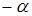
0
0
|
0
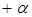
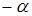
|
0
0
0
|

0
0
|
0


|
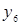
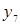

|
| Центр плана |
9
|
+1 |
0 |
0 |
0 |
0 |
0 |
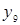 |
Аналогичным образом строятся планы и для большего числа факторов [1].
В общем виде план, представленный в таблице 1, неортогонален так как
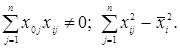 (9) (9)
Приведем его к ортогональному виду,
для чего введем новые переменные (преобразования для квадратичных эффектов):
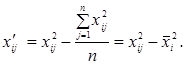 (10) (10)
при этом
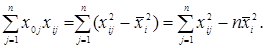 (11) (11)
Тогда уравнение регрессии будет записано как
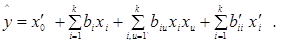 (12) (12)
Композиционные планы легко привести к ортогональным, выбирая звездное плечо  . В таблице 2 приведено значение а для различного числа факторов k и числа опытов в центре плана . В таблице 2 приведено значение а для различного числа факторов k и числа опытов в центре плана 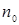 . .
Таблица 2 – Значения звездных плеч в ортогональных планах второго порядка
Число опытов в центре плана 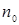 |
Звездное плечо  при различном числе факторов k при различном числе факторов k |
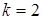 |
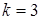 |
 |
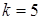
(в ядре полуреплики)
|
| 1 |
1,000 |
1,215 |
1,414 |
1,546 |
| 2 |
1,077 |
1,285 |
1,471 |
1,606 |
| 3 |
1,148 |
1,353 |
1,546 |
1,664 |
| 4 |
1,214 |
1,414 |
1,606 |
1,718 |
| 5 |
1,267 |
1,471 |
1,664 |
1,772 |
| 6 |
1,320 |
1,525 |
1,718 |
1,819 |
| 7 |
1,369 |
1,575 |
1,772 |
1,868 |
| 8 |
1,414 |
1,623 |
1,819 |
1,913 |
| 9 |
1,454 |
1,668 |
1,868 |
1,957 |
| 10 |
1,498 |
1,711 |
1,913 |
2,000 |
В частности, ортогональный план второго порядка для 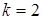 и и   представлен в таблице 3, а его геометрическая интерпретация - на рисунке 3, а. представлен в таблице 3, а его геометрическая интерпретация - на рисунке 3, а.
Представленный на рисунке 3, а и в таблице 3 прямоугольный (квадратный) план эксперимента для модели второго порядка работоспособен, хотя и несколько избыточен (9 опытов для определения 6 коэффициентов). Благодаря трем избыточным опытам, он позволяет усреднить случайные погрешности и оценить их характер.
Таблица 3 – Ортогональный центральный композиционный план второго порядка
| Номер опыта |
Факторы |
Результат |
 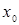 |
 |
 |
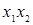 |
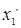 |
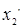 |
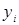 |
Ядро
плана
|
1
2
3
4
|
+1
+1
+1
+1
|
- 1
+1
- 1
+1
|
- 1
- 1
+1
+1
|
+1
- 1
- 1
+1
|
+1/3
+1/3
+1/3
+1/3
|
+1/3
+1/3
+1/3
+1/3
|
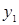


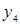
|
| Звездные точки |
5
6
7
8
|
+1
+1
+1
+1
|
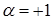

0
0
|
0
0
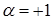

|
0
0
0
0
|
+1/3
+1/3
- 2/3
- 2/3
|
- 2/3
- 2/3
+1/3
+1/3
|

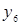
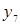

|
| Центр плана |
9 |
+1 |
0 |
0 |
0 |
- 2/3 |
- 2/3 |
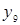 |
В этой таблице
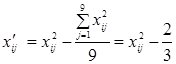 . (13) . (13)
В силу ортогональности матрицы планирования ее коэффициенты равны:
 (14) (14)
Уравнения регрессии 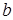 определяются независимо один от другого по формулам. определяются независимо один от другого по формулам.
Здесь i - номер столбца в матрице планирования; j - номер строки; суммы в знаменателях различны для линейных, квадратичных эффектов и взаимодействий.
Дисперсии коэффициентов уравнения регрессии следующие:
 . (15) . (15)
Следует особо отметить, что коэффициенты уравнения регрессии, получаемые с помощью ортогональных планов второго порядка, определяются с разной точностью (см. уравнение (14)), в то время как ортогональные планы первого порядка обеспечивают одинаковую точность коэффициентов, т.е. план, представленный в таблице 3, являющийся ортогональным и обеспечивающий независимость определения коэффициентов b, не является рототабельным.
В результате расчетов по матрице с преобразованными столбцами для квадратичных эффектов получаем уравнение регрессии в виде:
 (16) (16)
Для преобразования к обычной форме записи следует перейти от коэффициента 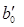 к коэффициенту к коэффициенту  , используя выражение: , используя выражение:
 . (17) . (17)
При этом дисперсия этого коэффициента рассчитывается по следующему соотношению:
 (18) (18)
В дальнейшем, зная дисперсию воспроизводимости, проверяют значимость коэффициентов и адекватность уравнения:
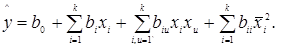 (19) (19)
Значимость коэффициентов проверяется по критерию согласия Стьюдента  . Коэффициент значим, если . Коэффициент значим, если  , где m– число степеней свободы дисперсии воспроизводимости. , где m– число степеней свободы дисперсии воспроизводимости.
Адекватность уравнения проверяется по критерию Фишера

Уравнение значимо, если составлено таким образом F - отношение меньше теоретического: 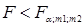 , где , где 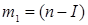 - число свободы дисперсии адекватности; - число свободы дисперсии адекватности; 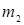 - число степеней свободы дисперсии воспроизводимости; I - число коэффициентов в уравнении регрессии второго порядка, равное числу сочетаний из - число степеней свободы дисперсии воспроизводимости; I - число коэффициентов в уравнении регрессии второго порядка, равное числу сочетаний из 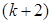 по 2, т.е. по 2, т.е.
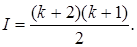 (20) (20)
Как было установлено, план второго порядка, представленный в таблице 3, не обладает свойством рототабельности. Рототабельным называют планирование, для которого дисперсия отклика (выходного параметра) 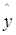 , предсказанного уравнением регрессии, постоянна для всех точек, находящихся на равном расстоянии от центра эксперимента. Экспериментатору заранее неизвестно, где находится та часть поверхности отклика, которая представляет для него особый интерес, поэтому следует стремиться к тому, чтобы количество информации, содержащееся в уравнении регрессии, было одинаково для всех равноотстоящих от центра эксперимента точек. Действительно, удаление от центра точек 5,6,7,8 в , предсказанного уравнением регрессии, постоянна для всех точек, находящихся на равном расстоянии от центра эксперимента. Экспериментатору заранее неизвестно, где находится та часть поверхности отклика, которая представляет для него особый интерес, поэтому следует стремиться к тому, чтобы количество информации, содержащееся в уравнении регрессии, было одинаково для всех равноотстоящих от центра эксперимента точек. Действительно, удаление от центра точек 5,6,7,8 в  раза меньше, чем удаление точек 1:
2, 3, 4 (см. рисунок 3,:
а), и, следовательно, коэффициент уравнения регрессии определяются с различной дисперсией. Бокс и Хантер предложили рототабельные планы 2-го порядка. Для того чтобы композиционный план был рототабельным, величину звездного плеча раза меньше, чем удаление точек 1:
2, 3, 4 (см. рисунок 3,:
а), и, следовательно, коэффициент уравнения регрессии определяются с различной дисперсией. Бокс и Хантер предложили рототабельные планы 2-го порядка. Для того чтобы композиционный план был рототабельным, величину звездного плеча  выбирают из условия: выбирают из условия:
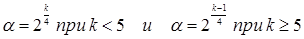  (21) (21)
Или в общем случае
 , ,
где k – число факторов;
p – дробность реплики (для ПФЭ p = 0, для полуреплики p =1, для четвертьреплики p = 2 и т.д.).
Число точек в центре плана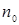 увеличивают. В таблице 4 приведены значения а для различного числа независимых факторов.
увеличивают. В таблице 4 приведены значения а для различного числа независимых факторов.
Таблица 4 - Значения звездных плеч и числа точек в центре ротатабельных планов
| Параметр плана |
Значение параметров при числе независимых факторов |
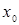 2 2 |
 3 3 |
 4 4 |
5 |
6 |
6 |
6 |
7 |
7 |
| Ядро плана |
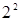 |
 |
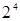 |
 |
 |
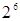 |
 |
 |
 |
| Звездное плечо |
1,414 |
1,682 |
2,00 |
2,378 |
2,00 |
2,828 |
2,378 |
3,333 |
2,828 |
Число точек в центре плана 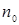
|
5 |
6 |
7 |
10 |
6 |
15 |
9 |
21 |
14 |
Рассмотрим идею выбора значения звездного плеча  на примере матрицы рототабельного планирования второго порядка для на примере матрицы рототабельного планирования второго порядка для 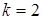 , представленной в таблице 5. , представленной в таблице 5.
Размещение точек этого плана показано на рисунке 3, б. Для обеспечения рототабельности точек 5, 6, 7, 8 необходимо удалить их от центра плана на расстояние  в в  раз большее, чем удаление точек 1, 2, 3, 4 от осей раз большее, чем удаление точек 1, 2, 3, 4 от осей и и  . В результате этого все точки плана (таблица 5) оказываются лежащими на окружности. Учитывая существенно большее влияние на функцию отклика случайной ошибки в точке 9, рекомендуется ставить в этой точке плана не один, а несколько дублирующих опытов (в данном случае опыты с 9 до 13) для усреднения полученных результатов и для осуществления статистического анализа результатов всего эксперимента в целом. . В результате этого все точки плана (таблица 5) оказываются лежащими на окружности. Учитывая существенно большее влияние на функцию отклика случайной ошибки в точке 9, рекомендуется ставить в этой точке плана не один, а несколько дублирующих опытов (в данном случае опыты с 9 до 13) для усреднения полученных результатов и для осуществления статистического анализа результатов всего эксперимента в целом.
Таблица 5 – Рототабельный план второго порядка
Учитывая специфический характер рототабельного плана в общем виде, можно также получить формулы для расчета коэффициентов уравнения регрессии и их дисперсий:
 (22) (22)
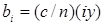 ; (23) ; (23)
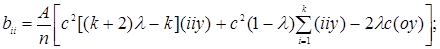  (24) (24)
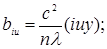 (25) (25)
 (26) (26)
 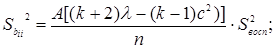 (27) (27)
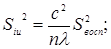 (28) (28)
где 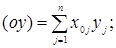  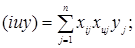 (29) (29)
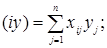  (30) (30)
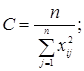 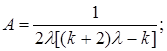 (31) (31)
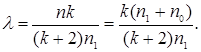 (32) (32)
Здесь 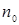 - число опытов в центре плана; - число опытов в центре плана; 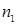 - число остальных опытов. - число остальных опытов.
Матрица рототабельного планирования, оказывается неортогональной, так как:
 (33) (33)
Следовательно, если какой-либо из квадратичных эффектов оказался незначимые, то после его исключения коэффициенты уравнения регрессии необходимо пересчитать заново.
При использовании рототабельных планов второго порядка дисперсию воспроизводимости можно определить по опытам в центре плана. В связи с этим при проверке адекватности уравнения регрессии, полученного по рототабельному плану второго порядка, поступают следующим образом.
Находят остаточную сумму квадратов:
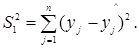 (34) (34)
с числом степеней свободы
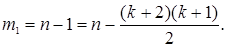 (35) (35)
По опытам в центре плана определяют сумму квадратов воспроизводимости:
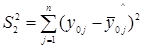 (36) (36)
с числом степеней свободы 
Далее находят сумму квадратов, характеризующих неадекватность 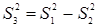 , число степеней свободы которой , число степеней свободы которой
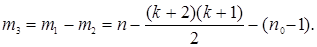 (37) (37)
Проверяют значимость по критерию согласия Фишера:
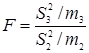 . (38) . (38)
Уравнение значимо, если 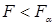
Если модель второго порядка оказалась неадекватной, следует повторить эксперименты на меньшем интервале варьирования факторов или перенести центр плана в другую точку факторного пространства. В тех случаях, когда адекватность модели по-прежнему не достигается, рекомендуется перейти к планам третьего порядка [1].
Использование теории планирования эксперимента является одним из путей существенного повышения эффективности многофакторных экспериментальных исследований. Под планированием эксперимента понимают процедуру выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. Основные преимущества активного эксперимента связаны с тем, что он позволяет:
1. Минимизировать общее число опытов;
2. Выбирать четкие логически обоснованные процедуры, последовательно выполняемые экспериментатором при проведении исследования;
3. Использовать математический аппарат, формализующий многие действия экспериментатора;
4. Одновременно варьировать всеми переменными и оптимально использовать факторное пространство;
5. Организовать эксперимент таким образом, чтобы выполнялись многие исходные предпосылки регрессионного анализа;
6. Получать математические модели, имеющие лучшие в некотором смысле свойства по сравнению с моделями, построенными из пассивного эксперимента;
7. Рандомизировать условия опытов, то есть многочисленные мешающие факторы превратить в случайные величины;
8. Оценивать элемент неопределенности, связанный с экспериментом, что дает возможность сопоставлять результаты, полученные разными исследователями.
В планировании экспериментов применяются в основном планы первого и второго порядков. Планы более высоких порядков используются в инженерной практике редко. В данном реферате было кратко изложена методика составления плана эксперимента для моделей первого порядка и более подробно представлено понятие о планировании второго порядка и построение планов второго порядка [2].
1. Спирин Н.А., Лавров В.В. Методы планирования и обработки результатов инженерного экспиремента: конспект лекции Н.А. Спирина – Екатеринбург: ГОУ ВПО УГТУ – УПИ, 2004.- 257 с.
2. Налимов В.Н. Логические основания планирования эксперимента: учебник Е.А. Шалыгина -2-е изд. – М.: Колос, 2001.
3. Планирование эксперимента – Режим доступа: URL: http://opds.sut.ru/electronic_manuals/pe/f053.htm
|