| Министерство образования Республики Беларусь
«Гомельский государственный университет им. Ф. Скорины»
Математический факультет
Кафедра МПМ
Реферат
Расширение понятия числа в школьном курсе математики
Исполнитель:
Студентка группы М-42
Малахова А.Ю.
аучный руководитель:
Канд. физ-мат. наук, доцент
Лебедева М.Т.
Гомель 2007
Введение
Понятие числа – стержневое понятие школьного курса математики. Линия развития понятия числа строится по принципу расширения множества А до множества В, при котором: 1) А должно быть подмножеством множества В; 2) операции над элементами из А те же, что и для элементов из В, но смысл тех операций, которые были только в множестве А, неизменным; 3) в множестве В должна быть выполнена операция, которая в множестве А была невыполнима или не всегда выполнима; 4) расширение В должно быть минимальным из всех расширений множества А.
1. Расширение понятия числа в школьном курсе математики
Преподавание вопросов связанных с развитием учения о числе учитель строит таким образом, чтобы ясна была связь понятий равенства, сумма и произведение, с одной стороны, и понятие числа, с другой. Таким образом, для того чтобы новые числа были равноправными, необходимо введение определения:
понятие равенства и установление критерия сравнения новых чисел между собой и с ранее известными числами;
понятие суммы;
понятие произведения.
Необходимо показать, что новые числа подчиняются всем законам арифметических действий, установленным для изучаемых ранее числам. Целесообразность вводимых определений иллюстрируют рассмотрением конкретных примеров. Каждый этап развития числа состоит из: 1) мотивировки
(алгебраический или алгебраический; например, появление отрицательных чисел – алгебраический, дробных чисел - практический); 2) подтверждение
.
Изучение арифметики натуральных чисел основано на наглядности. Учащиеся должны твердо усвоить, что любое натуральное число может быть изображено точкой на координатном луче, но не всякой точке на этом луче отвечает натуральное число. Этот последний факт готовит учащихся к пониманию необходимости введения новых чисел. Учащиеся знакомятся с одним из свойств множества натуральных чисел – бесконечностью. При изучении законов арифметических действий, для избегания формализма необходимо отметить их теоретическое значение. В частности, коммутативный и ассоциативный законы умножения целесообразно связать с геометрическим материалом (вычислением площадей прямоугольников, объёмом прямоугольных параллелепипедов).
2. Введение дробных чисел
Первое расширение понятия числа – введение дробных чисел. Пропедевтика обыкновенных дробей сводится к ознакомлению учащихся с такими вопросами, как доля единицы, изображение дробей на координатном луче, правильные и неправильные дроби, основное свойство дробей, представление натурального числа в виде дроби. Десятичная дробь рассматривается как частный случай обыкновенной дроби, как способ записи дробей со знаменателем вида 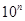 . Учащиеся должны иметь навыки чтения и записи десятичных дробей, умение записывать с помощью запятой числа вида . Учащиеся должны иметь навыки чтения и записи десятичных дробей, умение записывать с помощью запятой числа вида 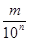 , где , где 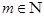 . Сравнение дробей основано на основном свойстве обыкновенной дроби и позволяет установить важное свойство десятичных дробей, состоящее в возможности приписывания и отбрасывания нулей справа. Изучение умножения и деления десятичных дробей начинается с “простого” случая умножения и деления дроби на натуральное число. На конкретных примерах учащиеся убеждаются в том, что и для этих чисел смысл операции сохраняется. . Сравнение дробей основано на основном свойстве обыкновенной дроби и позволяет установить важное свойство десятичных дробей, состоящее в возможности приписывания и отбрасывания нулей справа. Изучение умножения и деления десятичных дробей начинается с “простого” случая умножения и деления дроби на натуральное число. На конкретных примерах учащиеся убеждаются в том, что и для этих чисел смысл операции сохраняется.
3. Введение отрицательных чисел. Определения свойств действий над целыми числами
Следующее расширение понятия числа – знакомство учащихся с отрицательными числами. С методической стороны введение отрицательных чисел особых затруднений не представляет, т.к. дети часто встречаются в жизни. Наибольшую трудность в их изучении представляет обоснование действии над ними.
Введение понятия отрицательного числа требует дать определение:
модуля
(мотивировать это можно на конкретной задаче) как расстояние от точки, изображающей это число, до начальной точки. На основании такой геометрической интерпретации поясняется свойство модуля – он не может быть отрицательным, иначе говоря, модуль числа – есть число неотрицательное. Очень часто учащиеся считают его числом положительным, это можно объяснить отработкой учителя этого понятия, т.к. очень редко понятие расстояния связывается с начальной точкой(например, на каком расстоянии находится точка О от начальной точки?).
противоположных чисел
(основано на понятии симметричных точек).
Сравнение положительных и отрицательных чисел иллюстрируется конкретными примерами и с помощью геометрических образов, что позволяет подготовить учащихся к введению соответствующих определений. И так как множество рациональных чисел включает в себя множество натуральных чисел, то сравнение их необходимо проводить таким же образом.(Напомним: из двух натуральных чисел большее то из них, которое на координатной прямой правее и наоборот, если числа равны, то соответствующие им точки совпадают).
В школьном курсе определение действия обычно даётся в виде правила. Относительно операции сложения целых чисел, отдельно определяется сложение чисел с разными знаками и сложение отрицательных чисел. Для того чтобы учащихся подвести к определению действия сложения используются конкретные задачи на сложение чисел с помощью координатной прямой.
Умножение положительных и отрицательных чисел представляет наибольшую трудность. Правило знаков, которое даётся в школе, является по существу, своеобразной трактовкой определения операции умножения положительных и отрицательных чисел, а утверждения, которые на самом деле представляют собой определение новых понятий, не могут быть доказаны!
Существует два пути истолкования правила знаков: 1) предварительно рассматривается ряд задач, решение которых требует проводить вычисления по формуле вида 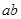 .
( .
(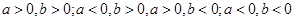 ). Недочёт метода в том, что:1)у учащихся создаётся впечатление того, что проводится доказательство правила умножения; 2)допущена логическая ошибка, ибо формула ). Недочёт метода в том, что:1)у учащихся создаётся впечатление того, что проводится доказательство правила умножения; 2)допущена логическая ошибка, ибо формула 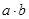 верна для верна для 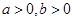 ; 2) догматический способ введения умножения
, предполагающий формирование правила умножения, которое затем поясняется на примерах и убеждает учащихся в целесообразности введенного определения. ; 2) догматический способ введения умножения
, предполагающий формирование правила умножения, которое затем поясняется на примерах и убеждает учащихся в целесообразности введенного определения.
Все числа с которыми учащиеся ознакомились, составляют новое множество рациональных чисел. Вводится определение рационального числа, как дроби вида 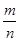 , где , где  . В этом множестве выполнимы сложение, вычитание, умножение и деление на число, не равное нулю. При выполнении дейсвий получаем числа того же мн-ва, т.е. это мн-во обладает свойством замкнутости по отношению к действиям первой и второй ступени. . В этом множестве выполнимы сложение, вычитание, умножение и деление на число, не равное нулю. При выполнении дейсвий получаем числа того же мн-ва, т.е. это мн-во обладает свойством замкнутости по отношению к действиям первой и второй ступени.
Для сложения справедливы: 1) переместительный закон 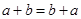 ; 2) сочетательный закон ; 2) сочетательный закон  ; 3) имеется нейтральный элемент ; 3) имеется нейтральный элемент  ; 4) ; 4)  , т.е. имеется противоположный элемент. , т.е. имеется противоположный элемент.
Для умножения справедливы следующие законы: 1) переместительный; 2) распределительный  (учащимся знакомо понятие алгебраической суммы, поэтому нет необходимости говорить раздельно о сложении и вычитании); 3) сочетательный закон; 4) (учащимся знакомо понятие алгебраической суммы, поэтому нет необходимости говорить раздельно о сложении и вычитании); 3) сочетательный закон; 4)  - нейтральный элемент; 5) - нейтральный элемент; 5) 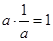 , - обратный элемент. , - обратный элемент.
4. Введение иррационального числа. Методическая схема введения действительного числа
Следующее расширение понятия числа – иррациональное число. В соответствии с построением множества действительных чисел по Дедекинду на множестве рациональных чисел существуют только три вида сечений: 1) в В нет наибольшего, в В` наименьшее(деление множества рациональных чисел по числу, например,2); 2) в В есть наибольшее, в В` нет наименьшего; 3) в В нет наибольшего числа, в В` нет наименьшего
Пример.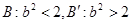 Докажем, что в В нет наибольшего числа. Докажем, что в В нет наибольшего числа.
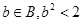 . Покажем, что можно подобрать такое целое положительное число n, для которого . Покажем, что можно подобрать такое целое положительное число n, для которого 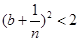 , т.е. , т.е. 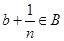 - доказать. - доказать. 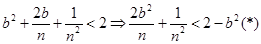 Если для неравенства Если для неравенства  найдётся n, для которого оно справедливо, то будет верно и данное неравенство: (*) найдётся n, для которого оно справедливо, то будет верно и данное неравенство: (*)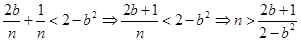 , т.е. число , т.е. число 
Так как во множестве рациональных чисел существует сечение третьего типа, то оно не является полным. Это сечение определяет число иррациональное. С геометрической точки зрения этот факт означает, что на координатной прямой существуют точки, которые не соответствуют никаким числам из множества рациональных чисел: множество рациональных чисел несвязно.
В школе при введении иррационального числа используют следующий факт: известно, что каждому рациональному числу r соответствует единственная точка M(r) прямой l, на которой заданы: начало отсчета, направление и масштаб. При этом число  называется координатой точки M. Верно ли обратное утверждение? Ответ иллюстрируется следующим примером: называется координатой точки M. Верно ли обратное утверждение? Ответ иллюстрируется следующим примером:
Докажем, что точка М не соответствует никакому рациональному числу.
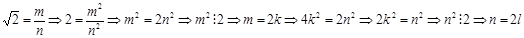 , что противоречит тому, что , что противоречит тому, что 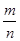 - несократимая дробь определение рационального числа). - несократимая дробь определение рационального числа).
Ещё один способ доказательства иррациональности числа  является построение последовательных рациональных приближений этого числа по недостатку и по избытку, которые обладают следующими свойствами: является построение последовательных рациональных приближений этого числа по недостатку и по избытку, которые обладают следующими свойствами:
1) каждое число последовательности (2) больше числа последовательности (1) с тем же номером: 1,4; 1,41; 1,414; 1,4142;…. (1)
1,5; 1,42; 1,415; 1,4143;…. (2)
2) последовательность (1)  ; (2) - ; (2) - 
3) разность между членами последовательностей с одинаковыми номерами неограниченно уменьшается по абсолютной величине при увеличении номера и равна 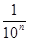 . Геометрически этот факт определяет сближение точек последовательности к . Геометрически этот факт определяет сближение точек последовательности к  . .
Иначе говоря, члены последовательностей (1) и (2) образуют непериодическую десятичную дробь.
Методическая схема введения действительного числа:
а) делается попытка решения уравнения 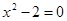 , т.е. необходимо доказать теорему: не существует ни целого, ни дробного числа, квадрат которого равнялся бы числу 2 , т.е. необходимо доказать теорему: не существует ни целого, ни дробного числа, квадрат которого равнялся бы числу 2
б) так как теорема доказана, то надо показать, что не существует целого числа, квадрат которого равен 2;
в) параллельно вводится понятие действительного числа на геометрической основе, т.е. в процессе измерения отрезков (отыскание абсциссы точки графика  , ордината которой равна 2). Такая задача приводит к проблеме измерения отрезка другим, принятым за единицу измерения; , ордината которой равна 2). Такая задача приводит к проблеме измерения отрезка другим, принятым за единицу измерения;
г) измерение отрезка. Соизмеримые и несоизмеримые отрезки. Десятичные приближения длины отрезка;
д) бесконечные периодические и непериодические дроби;
е) обращение обыкновенной дроби в бесконечную периодическую и обратная задача;
ж) иррациональные числа. Примеры;
з) действительные числа;
и) сравнение действительных чисел;
к) операции над действительными числами.
Следует помнить, что если в заданиях для следующих выражений:
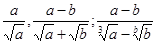 необходимо избавится от иррациональности в знаменателе, это означает, что в знаменателях этих дробей находятся иррациональные числа. В этом учащиеся могут убедиться, придав буквам конкретные значения. Алгебраические категории представляют собой абстракции более высокого порядка, а значит, рассуждения в алгебре носят более обобщённый характер, нежели непосредственно в числовых системах. необходимо избавится от иррациональности в знаменателе, это означает, что в знаменателях этих дробей находятся иррациональные числа. В этом учащиеся могут убедиться, придав буквам конкретные значения. Алгебраические категории представляют собой абстракции более высокого порядка, а значит, рассуждения в алгебре носят более обобщённый характер, нежели непосредственно в числовых системах.
Заключение
Изучение арифметики натуральных чисел основано на наглядности. Учащиеся должны твердо усвоить, что любое натуральное число может быть изображено точкой на координатном луче, но не всякой точке на этом луче отвечает натуральное число. Этот последний факт готовит учащихся к пониманию необходимости введения новых чисел. Учащиеся знакомятся с одним из свойств множества натуральных чисел – бесконечностью. При изучении законов арифметических действий, для избегания формализма необходимо отметить их теоретическое значение. В частности, коммутативный и ассоциативный законы умножения целесообразно связать с геометрическим материалом (вычислением площадей прямоугольников, объёмом прямоугольных параллелепипедов).
Литература
1. К.О. Ананченко «Общая методика преподавания математики в школе», Мн., «Унiверсiтэцкае»,1997г.
2. Н.М. Рогановский «Методика преподавания в средней школе», Мн., «Высшая школа», 1990г.
3. Г. Фройденталь «Математика как педагогическая задача»,М., «Просвещение», 1998г.
4. Н.Н. «Математическая лаборатория», М., «Просвещение», 1997г.
5. Ю.М. Колягин «Методика преподавания математики в средней школе», М., «Просвещение», 1999г.
6. А.А. Столяр «Логические проблемы преподавания математики», Мн., «Высшая школа», 2000г.
|