| КУРСОВОЙ ПРОЕКТ
по дисциплине:
«Основы конструирования»
на тему:
Проектирование механизмов и узлов оборудования электрических станций
Введение
Данный курсовой проект является самостоятельной работой студента, в процессе которой приобретаются и закрепляются навыки по решению комплекса инженерных задач: выполнение кинематических, силовых и прочностных расчетов узлов и деталей энергетического оборудования, выбор материалов, вида термической обработки и т.д.
Объектами курсового проектирования являются узлы и детали оборудования электростанций, а также системы их обеспечения. Например, в качестве питательных устройств для подачи воды применяют центробежные и поршневые насосы. В качестве арматуры для регулирования подачи теплоносителя или изменения его количества применяют задвижки и вентили. Задвижки и вентили выполняют фланцевыми, безфланцевыми, присоединяемыми к трубопроводу сваркой, и т.д. Для подготовки и подачи топлива служат пневмомеханические забрасыватели топлива, топки с движущейся колосниковой решеткой, пылеприготовительные устройства, мельницы-вентиляторы, валковые мельницы, дисковые питатели и др.
Все эти устройства в большинстве случаев состоят из исполнительного рычажного механизма (ИМ) и имеют привод, объединяющий электродвигатель 1, передачу гибкой связью 2 или зубчатую 3 и соединительные муфты 4 (Рис.2).
1. Исходные данные
Таблица 1
| Геометрические параметры
|

|
| 
|

|

|

|

|

|
10
|
| 110
|
450
|
130
|
0
|
0
|
0
|
| Силовые факторы
|
Схема
|
| 
|

|

|

|

|

|
2
|
| 1100
|
110
|
1200
|
120
|
400
|
–
|
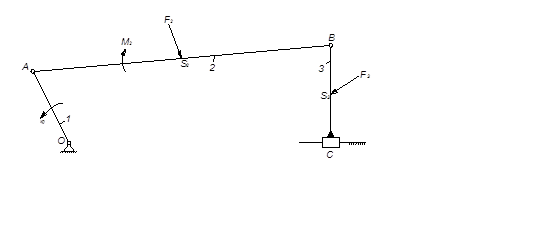
Рис.1 – Положение плоского рычажного механизма

Рис.2 – Типовой привод оборудования с передачами с гибкой и зубчатой связями
2. Кинематический анализ механизма
Произведем структурный анализ рычажного механизма. Степень подвижности плоского механизма рассчитаем по формуле Чебышева:
 ; ;  . .
· число подвижных звеньев:  ; ;
· число кинематических пар:  . .
| Пара
|
Звено
|
Класс
|
Вид
|
| 
|

|
5
|
вращ.
|
| 
|

|
5
|
вращ.
|
| 
|

|
5
|
вращ.
|
| 
|

|
5
|
пост.
|
Рассчитаем степень подвижности плоского механизма без ведущего звена:
 – 2 класс, 2 вид; – 2 класс, 2 вид;  . .

Рис.3 – Положение плоского рычажного механизма без ведущего звена
Рассчитаем степень подвижности ведущего звена:
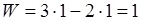 – 1 класс. Общий класс механизма – 2. – 1 класс. Общий класс механизма – 2.
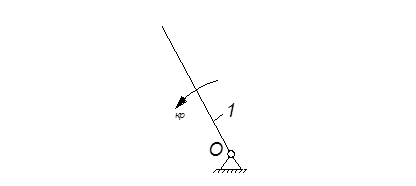
Рис.4 – Положение ведущего звена плоского рычажного механизма
2.1 Расчет скоростей
Построим схему заданного рычажного механизма в тринадцати положениях с шагом 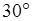 в следующем масштабе: в следующем масштабе:
 . .
Составим векторную систему уравнений, используя теорему об относительном движении:
  ; ; 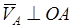 . .
Определим масштаб для построения плана скоростей:
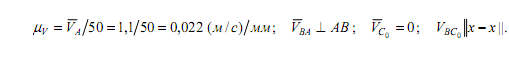
Зная величину и направление вектора скорости 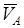 , а также зная линии действия других векторов скоростей, составим 13 планов скоростей механизма используя графо-аналитический метод. , а также зная линии действия других векторов скоростей, составим 13 планов скоростей механизма используя графо-аналитический метод.
Полученные результаты сведем в таблицу 2:
Таблица 2
| 
|


|
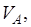

|
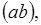

|


|


|
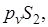

|


|
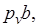

|


|
| 1.
|
50
|
1,1
|
52,39
|
1,15
|
2,56
|
26,2
|
0,58
|
15,64
|
0,34
|
| 2.
|
50
|
1,1
|
43,94
|
0,97
|
2,15
|
30,27
|
0,67
|
17,26
|
0,38
|
| 3.
|
50
|
1,1
|
24,94
|
0,55
|
1,22
|
44,22
|
0,97
|
41,5
|
0,91
|
| 4.
|
50
|
1,1
|
0
|
0
|
0
|
0
|
0
|
50
|
1,1
|
| 5.
|
50
|
1,1
|
25,14
|
0,55
|
1,23
|
45,9
|
1,01
|
45,05
|
0,99
|
| 6.
|
50
|
1,1
|
43,92
|
0,97
|
2,15
|
35,93
|
0,79
|
32,35
|
0,71
|
| 7.
|
50
|
1,1
|
52,31
|
1,15
|
2,56
|
26,13
|
0,57
|
15,29
|
0,34
|
| 8.
|
50
|
1,1
|
47,4
|
1,04
|
2,32
|
26,24
|
0,58
|
5,72
|
0,13
|
| 9.
|
50
|
1,1
|
28,87
|
0,64
|
1,41
|
38,19
|
0,84
|
28,87
|
0,64
|
| 10.
|
50
|
1,1
|
0
|
0
|
0
|
0
|
0
|
50
|
1,1
|
| 11.
|
50
|
1,1
|
28,87
|
0,64
|
1,41
|
52,04
|
1,14
|
57,74
|
1,27
|
| 12.
|
50
|
1,1
|
47,4
|
1,04
|
2,32
|
40,77
|
0,9
|
44,28
|
0,97
|
| 13.
|
50
|
1,1
|
52,39
|
1,15
|
2,56
|
26,2
|
0,58
|
15,64
|
0,34
|
2.2 План ускорений
План ускорений строим для положения механизма № 6. Составим векторную систему уравнений для построения плана ускорений:

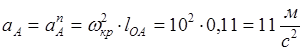 . .
 направлен по линии направлен по линии 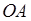 от от  к к  . .
 . .
 направлен по линии направлен по линии  от от  к к  . .
 ; ; 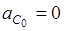 ; ;  ; ;  . .
Определим масштаб для построения плана ускорений:
 . .
Зная величину и направление векторов ускорения  и и  , а также зная линии действия других векторов ускорений, составим план ускорений механизма, используя графоаналитический метод. , а также зная линии действия других векторов ускорений, составим план ускорений механизма, используя графоаналитический метод.
Полученные в результате построения отрезки векторов 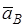 и и 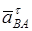 умножаем на масштаб умножаем на масштаб 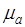 для получения действительного значения ускорений: для получения действительного значения ускорений:
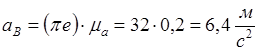 ; ;
 , тогда , тогда  . .
3. Силовой анализ механизма
План сил строим для положения механизма № 6. Силовой анализ механизма начинаем с рассмотрения отсоединенной структурной группы 2–3 второго класса, второго вида. Для определения  рассмотрим условие равновесия второго звена аналитическим методом: рассмотрим условие равновесия второго звена аналитическим методом:
 ; ;
 ; ;
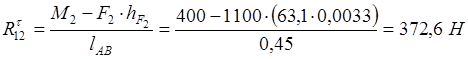 . .
Направление и численные значения  и и  определим из условия равновесия структурной группы: определим из условия равновесия структурной группы:
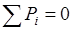 ; ;
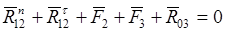 . .
Для построения плана сил необходимо выбрать масштаб:
 ; ;
 ; ;  . .
Полученные в результате построения отрезки векторов умножаем на масштаб для получения действительного значения сил:
 ; ;
 ; ;
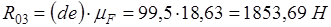 . .
Для определения  рассмотрим условие равновесия третьего звена: рассмотрим условие равновесия третьего звена:
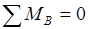 ; ;
 ; ;
 . .
Для определения 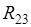 во внутренней паре во внутренней паре  (шарнир) рассмотрим условие равновесия третьего звена: (шарнир) рассмотрим условие равновесия третьего звена:
 ; ;
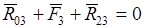 . .
Найдем графически из построения:
 ; ;  . .
Из условия равновесия первого звена определяем уравновешивающую силу  : :
 ; ;
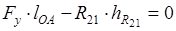 ; ;
 . .
Для определения направления и численного значения 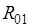 используют условие равновесия первого звена: используют условие равновесия первого звена:
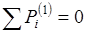 ; ;
 . .
Выберем новый масштаб:
 . .
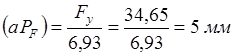 ; ;  ; ;
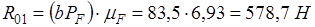 . .
4. Расчет уравновешивающих сил методом рычага Жуковского
Используя теорему «О рычаге Жуковского» переносим с поворотом на 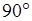 все силы, действующие на механизм, на план скоростей в соответствующие точки: все силы, действующие на механизм, на план скоростей в соответствующие точки:
 – уравновешивающая сила, действующая в точку – уравновешивающая сила, действующая в точку  ; ;
 – сила, действующая на второе звено в точку – сила, действующая на второе звено в точку   ; ;
 – сила, действующая на третье звено в точку – сила, действующая на третье звено в точку 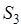  ; ;
 – действующий момент представляем как пару сил, которые равны: – действующий момент представляем как пару сил, которые равны:
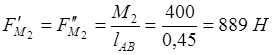 . .
Из плана скоростей определяем уравновешивающую силу, исходя из условия равновесия плана скоростей для каждого положения механизма:
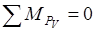 . .
Положение 1, 13:

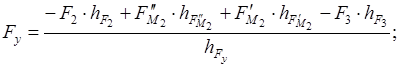

Положение 2:

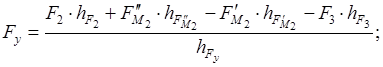

Положение 3:
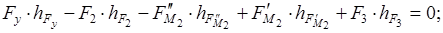
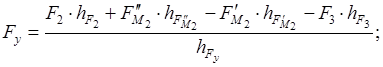
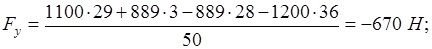
Положение 4:


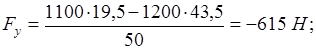
Положение 5:

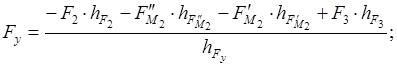

Положение 6:
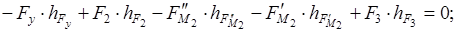


Положение 7:



Положение 8:



Положение 9:



Положение 10:



Положение 11:



Положение 12:

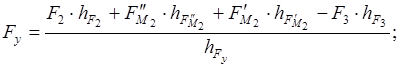

Полученные результаты сведем в таблицу 3.
Таблица 3
| 
|


|


|


|


|


|


|


|


|


|


|


|
| 1.
|
1100
|
15
|
1200
|
14
|
889
|
48
|
889
|
5
|
-276
|
0,11
|
30,36
|
| 2.
|
1100
|
29
|
1200
|
15
|
889
|
47
|
889
|
3
|
-504
|
0,11
|
55,44
|
| 3.
|
1100
|
29
|
1200
|
36
|
889
|
28
|
889
|
3
|
-670
|
0,11
|
73,7
|
| 4.
|
1100
|
19,5
|
1200
|
43,5
|
889
|
0
|
889
|
0
|
-615
|
0,11
|
67,65
|
| 5.
|
1100
|
6,6
|
1200
|
39,1
|
889
|
22
|
889
|
3,2
|
-345,14
|
0,11
|
37,97
|
| 6.
|
1100
|
4,4
|
1200
|
28,1
|
889
|
38,2
|
889
|
5,7
|
9
|
0,11
|
-0,99
|
| 7.
|
1100
|
15,3
|
1200
|
13,3
|
889
|
47,8
|
889
|
4,5
|
274
|
0,11
|
-30,14
|
| 8.
|
1100
|
26,2
|
1200
|
5
|
889
|
49,7
|
889
|
2,3
|
386
|
0,11
|
-42,46
|
| 9.
|
1100
|
35,7
|
1200
|
25,1
|
889
|
43,3
|
889
|
14,5
|
329
|
0,11
|
-36,19
|
| 10.
|
1100
|
39,5
|
1200
|
43,4
|
889
|
0
|
889
|
0
|
173
|
0,11
|
-19,03
|
| 11.
|
1100
|
30,7
|
1200
|
50,12
|
889
|
0
|
889
|
28,95
|
-13
|
0,11
|
1,43
|
| 12.
|
1100
|
11,2
|
1200
|
38,4
|
889
|
29,3
|
889
|
18,03
|
-166
|
0,11
|
18,26
|
| 13.
|
1100
|
15
|
1200
|
14
|
889
|
48
|
889
|
5
|
-276
|
0,11
|
30,36
|
5. Расчет элементов привода
Исходные данные:
| 
|

|
| 74
|
10
|
5.1 Выбор электродвигателя
Номинальная мощность электродвигателя:
 . .
Требуемая мощность электродвигателя:
 , ,
где  – коэффициент полезного действия привода; – коэффициент полезного действия привода;
 – номинальная мощность, – номинальная мощность,  . .
По каталогам выбираем электродвигатель с ближайшей большей номинальной мощностью  и номинальной частотой вращения ротора и номинальной частотой вращения ротора 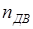 . .
Характеристики выбранного электродвигателя:
· Двигатель асинхронный трехфазный, марки 4А90В8УЗ;
· 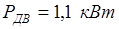 ; ;
·  ; ;
·  ; ;
·  . .
Передаточное отношение привода:
 , где , где  . .

Принимаем  , тогда , тогда  . .
5.2 Расчет диаметра вала
Диаметр вала  передаточного или исполнительного механизма определяется по следующей зависимости: передаточного или исполнительного механизма определяется по следующей зависимости:
 , где , где  ; ;
 . .
Полученное значение округлим до ближайшего большего значения стандартного ряда диаметров. Принимаем  . .
5.3 Расчет фланцевой муфты
Расчетный вращающий момент

где  – коэффициент режима работы. – коэффициент режима работы.
Соотношения между размерами муфты
· наружный диаметр:
 . Тогда выберем . Тогда выберем  ; ;
· диаметр ступицы:
 ; ;
· общая длина:
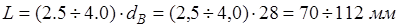 . .
Тогда выберем  ; ;
Материал муфты при окружной скорости на наружных поверхностях фланцев  выбираем Сталь 45. выбираем Сталь 45.
Расчет болтового соединения
Окружная сила на болты от действия вращающего момента:

где  – диаметр окружности центров болтов. – диаметр окружности центров болтов.
 . .
Сила, приходящаяся на один болт:
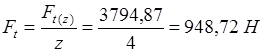
где  – назначенное число болтов. – назначенное число болтов.
Допускаемые напряжения устанавливаем в зависимости от выбранного материала:
· допускаемые напряжения на срез:
 ; ;
· допускаемые напряжения на смятие:
 . .
Рассчитываем диаметр болта по следующей зависимости:
 , ,
где  – число плоскостей среза болта. – число плоскостей среза болта.
Принимаем болт с ближайшим большим стандартным диаметром  . Выбираем болт по ГОСТу 7796-70, а именно болт М6: . Выбираем болт по ГОСТу 7796-70, а именно болт М6:
| 
|

|

|

|
 – длина болта, – длина болта, 
|
 - длина резьбы, - длина резьбы, 
|
| 6
|
10
|
11,1
|
4
|
30
|
18
|
Выбираем соответствующую гайку и шайбу:
| 
|
Гайка
|
Шайба
|
| 
|

|

|

|

|
| 6
|
10
|
10,9
|
5
|
6,1
|
1,4
|
Назначаем посадочный диаметр болта в отверстие полумуфты (рекомендуемая посадка –  ): ):
 . .
Толщину дисков полумуфты фланцевой муфты принимаем из конструктивных соображений:  . .
Вычисляем напряжения смятия и сравниваем с допускаемыми:

т.о. условие соблюдается.
5.4 Расчет предохранительного устройства
Момент  срабатывания муфты в качестве предохранительного устройства: срабатывания муфты в качестве предохранительного устройства:
 , ,
где  – коэффициент запаса. – коэффициент запаса.
5.5 Расчет посадки полумуфты на вал
Расчет соединения с натягом
Диаметр соединения  , условный наружный диаметр ступицы , условный наружный диаметр ступицы  , вал сплошной , вал сплошной  , ,  – длина ступицы, класс точности изготовления (обычно 2-ой или 3-ий), шероховатости вала и отверстия – длина ступицы, класс точности изготовления (обычно 2-ой или 3-ий), шероховатости вала и отверстия    . .
Значение коэффициента трения зависит от способа сборки, удельного давления, шероховатости поверхности, рода смазки поверхностей применяемой при запрессовке деталей, скорости запрессовки и прочие. В расчетах принимаем:  – сборка прессованием. – сборка прессованием.
Определяем давление, обеспечивающее передачу заданной нагрузки:
 , ,
где  . .
Определим расчетный натяг при значениях коэффициентов Пуассона  и модулей упругости и модулей упругости  : :

где  и и  - масштабные коэффициенты. - масштабные коэффициенты.
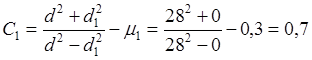 ; ;
 ; ;
Определяем минимальный требуемый натяг с учетом шероховатости:
 . .
Намечаем посадку:
Ø28  ; Ø28 ; Ø28  ; Ø28 ; Ø28  ; ;
 ; ;  . .
Т.к.  , то данная посадка подходит. , то данная посадка подходит.
Определяем наибольший вероятный натяг без учета сглаживания микронеровностей:
 . .
Максимальное давление в контакте:
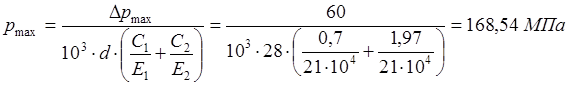 . .
Определяем окружные и радиальные напряжения:
 ; ;
 . .
Выбираем предел текучести для материала с меньшей прочностью (для Сталь 45):  . .
Т.к.  ,то условие прочности выполняется. ,то условие прочности выполняется.
Усилие запрессовки:
 , ,
где  – давление, которое рассчитывается при – давление, которое рассчитывается при  : :
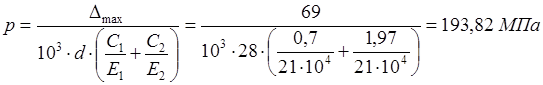 . .
5.6 Расчет шпоночного и зубчатого соединения
Расчет шпоночного соединения
Применяем ненапряженное соединение с помощью призматической шпонки. Размеры в соединении выбираем по стандарту. Стандартные шпонки изготавливают из специального сортамента (ГОСТ 8787-68 и 8786-68) среднеуглеродистой чисто тянутой Стали 45.
Допускаемые напряжения в неподвижных шпоночных соединениях:
 . .
По диаметру вала  выбираем по ГОСТу 23360-78 размеры сечения призматической шпонки выбираем по ГОСТу 23360-78 размеры сечения призматической шпонки  , а также глубину паза вала , а также глубину паза вала 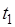 и втулки и втулки  . .
| Размер шпонки
|
Глубина паза
|
| Вал
|
Втулка
|
| 
|

|

|

|

|
| 8
|
7
|
50
|
4
|
3,3
|
Рассчитаем длину ступицы  : :
 . .
Длину шпонки  принимаем на принимаем на  меньше длины ступицы меньше длины ступицы  : :
 . .
Рассчитаем рабочую длину шпонки со скруглениями:
 . .
Проверочный расчет выбранной шпонки выполняем для наименее прочного элемента шпоночного соединения.
Расчет проводим по условию прочности на смятие:
 . .
Расчет зубчатого соединения
Применяем прямобочное шлицевое соединение, основные размеры которого регламентированы ГОСТом 6033-80. По диаметру вала выберем размеры шлицевого соединения легкой серии:
| Диаметр вала

|

|

|

|

|
| 28
|
32
|
7
|
6
|
0,3
|
Для неподвижного соединения, средних условий эксплуатации допускаемые напряжения смятия для поверхности зуба:
 . .
Проверим соединение на смятие:
 , ,
где  – средний диаметр соединения; – средний диаметр соединения;
 – рабочая высота зубьев; – рабочая высота зубьев;
 – длина соединения; – длина соединения;
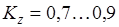 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями. – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями.
6. Расчет вала и подшипников качения
Исходные данные:
6.1 Расчет вала
Ориентировочная взаимосвязь между указанной исходной величиной и другими геометрическими параметрами вала:
 ; ;
 ; ;
 ; ;
По полученному в результате предварительного расчета значению  произведем выбор подшипника легкой серии диаметров (ГОСТ 8338-75): произведем выбор подшипника легкой серии диаметров (ГОСТ 8338-75):
| Условное обозначение
|

|

|

|

|

|
| 208
|
40
|
80
|
18
|
32,0
|
17,0
|
Для крышки выбираем манжету  по ГОСТу 8752-79. по ГОСТу 8752-79.
Под отверстия выбранной крышки выбираем болты по ГОСТу 7796-70, а именно болты М8:
| 
|

|

|

|
 – длина болта, – длина болта, 
|
 - длина резьбы, - длина резьбы, 
|
| 8
|
12
|
13,1
|
5
|
25
|
25
|
Выбираем соответствующие пружинные шайбы по ГОСТу 6402-70:
6.2 Поверочный расчет вала
Рассчитаем реакции опор:
 ; ;
 ; ;  , ,
где  ; ;  . .
 ; ;
 ; ;  . .
Проведем проверку:
 ; ;
 ; ;  . .
Построим эпюры изгибающих и крутящих моментов:
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;  ; ;

 ; ;
 . .
Выбираем несколько опасных сечений, которым соответствуют наибольшие ординаты эпюр и в которых имеются концентраторы напряжений:
 ; ;
 . .
Для каждого из отобранных сечений рассчитываем критерий напряженности:
 , ,
где  – усредненный коэффициент концентрации при изгибе и кручении в данном сечении; – усредненный коэффициент концентрации при изгибе и кручении в данном сечении;
 – изгибающий момент рассматриваемого сечения; – изгибающий момент рассматриваемого сечения;
 – крутящий момент; – крутящий момент;
 – момент сопротивления изгибу. – момент сопротивления изгибу.
 ; ;
 ; ;
 ; ;
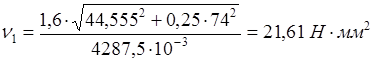 ; ;
 . .
Сечение, для которого  имеет максимальное значение, считается наиболее опасным и подлежит дальнейшему расчету. имеет максимальное значение, считается наиболее опасным и подлежит дальнейшему расчету.
Назначим материал вала – Сталь 45.
Установим пределы выносливости для материала вала при симметричном цикле изгиба и кручения:

 . .
где  – предел прочности материала. – предел прочности материала.
В опасном сечении вала определим расчетный коэффициент запаса прочности:
 , ,
где  и и 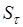 – коэффициенты запаса по нормальным и касательным напряжениям: – коэффициенты запаса по нормальным и касательным напряжениям:

 . .
Параметры симметричного цикла изменения напряжения при изгибе:
· амплитуда:
 , ,
где  – изгибающий момент в опасном сечении; – изгибающий момент в опасном сечении;
· среднее значение цикла:
 . .
Амплитуда и среднее значение от нулевого цикла изменения напряжения при кручении:
 , ,
где  . .
Эффективные коэффициенты концентрации напряжений детали определяю из выражений:
 ; ;
 , ,
где  ; ;  – эффективные коэффициенты концентрации напряжений при расчете на изгиб и кручение; – эффективные коэффициенты концентрации напряжений при расчете на изгиб и кручение;
 ; ;  – коэффициенты влияния абсолютных размеров поперечного сечения (масштабные факторы); – коэффициенты влияния абсолютных размеров поперечного сечения (масштабные факторы);
 ; ;  – коэффициенты качества обработки поверхности; – коэффициенты качества обработки поверхности;
 – коэффициент упрочняющей обработки; – коэффициент упрочняющей обработки;
 ; ;  – коэффициенты чувствительности к асимметрии цикла. – коэффициенты чувствительности к асимметрии цикла.
Сопоставляем расчетный коэффициент запаса прочности  c допустимым значением c допустимым значением  : :
 . .
6.3 Поверочный расчет подшипников качения на долговечность
Условие обеспечения долговечности подшипника:
 , ,
где  – расчетная долговечность подшипника, – расчетная долговечность подшипника,  ; ;
 – установленный ресурс (заданный ресурс) подшипника, который равен: – установленный ресурс (заданный ресурс) подшипника, который равен:
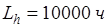 . .
Расчетная долговечность подшипника определяется из соотношения:

т. о. условие соблюдается.
где  – динамическая грузоподъемность; – динамическая грузоподъемность;
 – эквивалентная нагрузка; – эквивалентная нагрузка;
 – показатель степени для шарикоподшипников; – показатель степени для шарикоподшипников;
 – частота вращения подшипника: – частота вращения подшипника:
 . .
Эквивалентную нагрузку для радиальных и радиально-упорных подшипников рассчитаем по следующей формуле:
 , ,
где 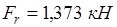 ; ;  – радиальная и осевая нагрузка на подшипник; – радиальная и осевая нагрузка на подшипник;
 – коэффициент вращения, при вращении внутреннего кольца; – коэффициент вращения, при вращении внутреннего кольца;
 – коэффициент безопасности; – коэффициент безопасности;
 – температурный коэффициент, при – температурный коэффициент, при 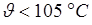 ; ;
 – для радиальных шарикоподшипников. – для радиальных шарикоподшипников.
 6.4 Эпоры изгибающих и крутящих моментов 6.4 Эпоры изгибающих и крутящих моментов
Рис.5 – Эпюры изгибающих и крутящих моментов
Список использованной литературы
1. Орлов В.А., Кравцов Э.Д. Детали машин и основы конструирования: Конспект лекций. – Одесса: ОПИ, 1991;
2. Методические указания к курсовому проектированию по курсу «Детали машин и основы конструирования» «Расчет зубчатых зацеплений, валов и подшипников цилиндрического редуктора» для студентов всех специальностей /Сост.: В.А. Орлов, Э.Д. Кравцов. – Одесса: ОПИ, 1993;
3. Курсовое проектирование деталей машин /В.Н. Кудрявцев и др. – Л.: Машиностроение, Ленингр. отд-ние, 1984;
4. Цехнович Л.И., Петренко И.П. Атлас конструкций редукторов. – К.: Вища шк., 1979;
5. Подшипники качения: Справочник-каталог /Под ред. В.Н. Нарышкина и Р.В. Коросташевского. – М.: Машиностроение, 1984.
|