| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ
Кафедра радиоуправления и связи
КУРСОВОЙ ПРОЕКТ
по дисциплине “Радиосистемы передачи информации”
на тему “Система сжатия и уплотнения каналов”
Выполнил:
Руководитель:
Рязань, 2007
Содержание
Оглавление
Содержание.
Техническое задание.
Введение.
Определение частоты опроса.
Адаптивная дискретизация.
РИКМ..
Структурная схема и описание системы уплотнения.
Структура группового сигнала.
Основные временные диаграммы системы..
Заключение.
Список литературы..
Техническое задание
Вероятность ошибки на символ………………………………10-4
Показатель верности, %…...…………………….………….…0,3
Спектр сигнала…………………………………………………равномерный
Ширина спектра сигнала, Гц.…………………………………200
ФПВ сигнала…………………………………………………….норм.
Число каналов…………………………………………….……..50
Тип квантователя……………………………………..…………РИКМ
Уплотнение…………………………………………………..…по форме
Алгоритм сжатия………………………………………..………АД
Отношение с/ш квантователя, дБ……….……………………..30
Вид модуляции…………………………………………………ОФМ
Введение
В данном курсовом проекте разрабатывается система сжатия и уплотнения каналов, и определяются её основные параметры и характеристики. Проектирование и применение подобных систем в настоящее время считаются целесообразным, т. к. эти системы позволяют уменьшить плотность и сложность линий связи, увеличить число каналов, улучшить качество обслуживания абонентов, а так же предоставлять им дополнительные услуги.
Определение частоты опроса
 В нашем случае спектр сигнала равномерный. Определим частоту опроса F0
. По заданию на проект, показатель верности g
эф = 0.3 %
, а ширина спектра сигнала D
f
=200
Гц. Применим эту модель к интерполяции по Лагранжу при n
=1,2,3,
используя также следующие соотношения: В нашем случае спектр сигнала равномерный. Определим частоту опроса F0
. По заданию на проект, показатель верности g
эф = 0.3 %
, а ширина спектра сигнала D
f
=200
Гц. Применим эту модель к интерполяции по Лагранжу при n
=1,2,3,
используя также следующие соотношения:

Теперь проанализируем полученные результаты. Частота опроса F02
имеет существенный выигрыш по сравнению с F01
и проигрывает частоте F03
, так как больше неё. Но выберем F02
, так как при реализации на этой частоте обеспечивается заданное качество и используются небольшие аппаратные затраты.
Адаптивная дискретизация
В системе с адаптивной дискретизацией в каждом измерительном канале сужение полосы пропускания частот канала связи может быть получено без буферной связи. При этом передача информации будет производиться в реальном масштабе времени, что является достоинством таких систем, именно поэтому мы выбрали эту структурную схему.
Структурная схема передающей части ТИС
с адаптивной дискретизацией в каждом канале без буферной памяти представлена на рис.2. В литературе такие системы названы асинхронно-циклическими. Схема работает следующим образом. Сигналы с датчиков Д
анализируются адаптивными временными дискретизаторами АВД
, которые решают задачу адаптивной дискретизации в каждом измерительном канале отдельно. Если в каком-либо канале погрешность аппроксимации достигает значения заданной допустимой погрешности eд
, то на выходе соответствующего АВД
появится сигнал 1. В то же время импульсы от генератора тактовых импульсов ГТИ
через открытую схему запуска СЗ
с помощью распределителя Р
поочерёдно поступают на схемы совпадения И
.
Если на втором входе какой-либо схемы И
появляется сигнал 1 от АВД
, то схема И
выдаёт сигнал 1 на ключ К
и соответствующий датчик подключается к аналого-цифровому преобразователю АЦП
. При этом через собирательную схему ИЛИ
подаётся сигнал на СЗ
, запрещающий дальнейшее прохождение импульсов с ГТИ
до окончания преобразования и выдачи кода в линию связи. Распределитель останавливается, и параметр выбранного датчика преобразуется в код АЦП
, который поступает в блок считывания БС
. В БС
поступает также код номера (адрес) выбранного канала. В БС
код адреса и код параметра преобразуются из параллельного в последовательный и передаются в линию связи. По окончании считывания БС
выдаёт сигнал на разрешение дальнейшего прохождения импульсов через СЗ
на распределитель. Кроме того, сигнал окончания считывания от БС
поступает также на один из входов схемы совпадения И1
, служащей для формирования сигнала сброса АВД
в момент отсчёта.
Так как на второй вход схемы И1
поступает сигнал от схемы И
своего канала, то сброс АВД
произойдёт только в выбранном канале. После этого распределитель Р
продолжает опрос схем И
, причём время прохождения канала, у которого погрешность аппроксимации меньше заданной, выбирается малым по сравнению со временем преобразования сигнала и выдачи сигнала в линию связи.
В асинхронно-циклических системах можно не передавать код адреса, а вместо него через канал связи передавать на приёмную сторону импульсы переключения распределителя Р
от схемы запуска СЗ
.
РИКМ
Рассмотрим особенности работы разностного квантователя (рис. 3):
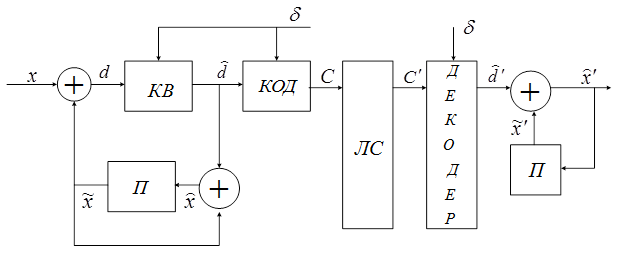 На входе квантователя действует сигнал:
 . .
Сигнал  называется погрешностью предсказания или разностный сигнал. Квантованию подвергается не входной, а разностный сигнал. Квантователь может быть адаптивным или неадаптивным, равномерным или неравномерным, но во всех случаях его параметры соответствуют дисперсии погрешности предсказания. Квантованная погрешность предсказания имеет вид: называется погрешностью предсказания или разностный сигнал. Квантованию подвергается не входной, а разностный сигнал. Квантователь может быть адаптивным или неадаптивным, равномерным или неравномерным, но во всех случаях его параметры соответствуют дисперсии погрешности предсказания. Квантованная погрешность предсказания имеет вид:
 , ,
где  - ошибка квантования разностного сигнала. Из структурной схемы следует, что квантованное значение исходного сигнала имеет вид: - ошибка квантования разностного сигнала. Из структурной схемы следует, что квантованное значение исходного сигнала имеет вид:

И используя формулы получаем выражение:
 . .
Таким образом квантованный входной сигнал отличается от исходного входного сигнала на величину шума квантования разностного сигнала, если предсказатель хороший, то дисперсия разностного сигнала будет меньше дисперсии входного сигнала и квантователь с заданным количеством уровней даст меньшую погрешность при квантовании разности, чем при квантовании исходного сигнала. Отношение с/ш квантования в этом случае имеет вид:
 , ,
где  - с/ш квантователя, - с/ш квантователя,  - коэффициент усиления, обусловленный разностным кодированием. Отношение с/ш квантователя зависит только от свойств квантователя (равномерный, неравномерный, адаптивный) и разностного сигнала. Величина - коэффициент усиления, обусловленный разностным кодированием. Отношение с/ш квантователя зависит только от свойств квантователя (равномерный, неравномерный, адаптивный) и разностного сигнала. Величина  определяет выигрыш в отношении с/ш при использовании разностного представления. Т.к. величина определяет выигрыш в отношении с/ш при использовании разностного представления. Т.к. величина  фиксированная, то увеличить коэффициент усиления можно только за счет минимизации фиксированная, то увеличить коэффициент усиления можно только за счет минимизации  . Для решения этой задачи определяют тип предсказателя. Рассмотрим возможность использования линейного предсказателя: . Для решения этой задачи определяют тип предсказателя. Рассмотрим возможность использования линейного предсказателя:
 , ,
где  - порядок фильтра предсказателя. Дисперсия погрешности предсказателя в этом случае имеет вид: - порядок фильтра предсказателя. Дисперсия погрешности предсказателя в этом случае имеет вид:
 . .
Дифференцируя  по по  и приравниваем к нулю, получим систему уравнений: и приравниваем к нулю, получим систему уравнений:
 . .
Решением системы уравнений будет  , при котором , при котором  минимальна. В этом случае коэффициент усиления: минимальна. В этом случае коэффициент усиления:
 , ,
где  - нормированная корреляционная функция - нормированная корреляционная функция  . Таким образом пока . Таким образом пока  отношение с/ш квантования будет увеличиваться за счет предсказания. отношение с/ш квантования будет увеличиваться за счет предсказания.
В случае речевого сигнала при  получаются зависимости коэффициента усиления получаются зависимости коэффициента усиления  от порядка фильтра предсказателя (рис. 4): от порядка фильтра предсказателя (рис. 4):

Даже при простом предсказателе, когда p=1, можно получить выигрыш в 6 дБ, что эквивалентно добавления одного разряда в квантователь.
В данной курсовой выберем линейный предсказатель второго порядка
В дальнейшем предполагаем, что шум квантования является стационарным белым шумом, некоррелированным с входным сигналом и имеющим равномерное распределение в интервале  в этом случае дисперсия шумов квантования: в этом случае дисперсия шумов квантования:

 или в децибелах или в децибелах  отсюда видно чтобы обеспечить с/ш равное 30дБ нужен 5-битный квантователь. отсюда видно чтобы обеспечить с/ш равное 30дБ нужен 5-битный квантователь.
Структурная схема и описание системы уплотнения.
При разделении каналов по форме (РКФ) базисные функции  должны быть минимально независимыми и желательно ортогональными. При этом передаваемая информация заключена в амплитуде базисных функций. В этом случае канальный сигнал будет иметь следующий вид: должны быть минимально независимыми и желательно ортогональными. При этом передаваемая информация заключена в амплитуде базисных функций. В этом случае канальный сигнал будет иметь следующий вид:

где  , ,  - период канального сигнала, - период канального сигнала,  - отсчёты первичного сигнала. - отсчёты первичного сигнала.
Эта формула справедлива, если информация заключена в амплитуде сигнала. В качестве базисных функций используются функции, удобные с точки зрения технической реализации. Обычно используются из-за лучшей помехоустойчивости ортогональные функции Чебышева, Лежандра, Матье, Уолша.
Ортогональные функции Лежандра, Чебышева являются непрерывными аналоговыми сигналами и, следовательно, устройствам их генерирования и обработки свойственны недостатки, присущие всем аналоговым устройствам: невозможность унификации, стандартизации, высокие требования к температурной стабильности, сложная техническая реализация и т.д.
Поэтому в настоящее время часто в качестве базисных функций используются ансамбли цифровых сигналов, в частности ансамбль функций Уолша. Именно эти функции и будем использовать в качестве базисных функций в данном курсовом проекте.
Структурная схема передающей части системы с ортогональными сигналами приведена на рис.5.

На схеме использованы следующие обозначения:
ГТЧ – генератор тактовой частоты; ГНК – генератор несущего колебания; Кi – ключи; ГПФ – генератор полиномиальных функций; СУ – суммарный усилитель; С – синхронизатор, M – модулятор (ОФМ).
На передающей стороне ГТЧ формирует кратковременные импульсы с частотой повторения. Ключи хранят значение весь период повторения. Синхронизатор формирует синхросигнал. Групповой сигнал имеет вид:

Для разделения сигналов по форме на приёмной стороне используют свойство ортогональности базисных функций. Математически эта операция выглядит так:

Структурная схема приёмной части приведена на рис.6.
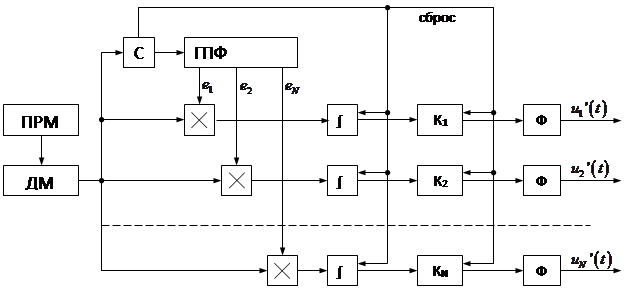
На схеме использованы следующие обозначения: ДМ – демодулятор; Ф – фильтры.
На приёмной стороне в синхронизаторе осуществляется выделение синхросигнала, который запускает ГПФ и сбрасывает интеграторы и ключи. Выделение информации осуществляется в соответствии с приведённым выше алгоритмом.
Как уже отмечалось, в качестве базисных функций будем использовать функции Уолша. Эти функции известны с 1922 г., но практический интерес к ним возник только в последние 2 – 3 десятилетия в связи с развитием ЭВМ. Существует множество способов задания (определения) функций Уолша.
Функции Уолша образуют полную ортонормированную систему из  функций и определяется через функции Радемахера следующим образом: функций и определяется через функции Радемахера следующим образом:

где  - номер функции в десятичном счислении; - номер функции в десятичном счислении;
 - n
– й разряд представления числа - n
– й разряд представления числа  в двоичной системе счисления; в двоичной системе счисления;
 - порядок функции Радемахера; - порядок функции Радемахера;
 - функции Радемахера; первые четыре имеют следующий вид - функции Радемахера; первые четыре имеют следующий вид
Для данной системы необходимо 8 функций Уолша, так как на вход системы уплотнения по форме поступают 8 сигналов с 7 адаптивных дискретизаторов. Образование необходимых нам функций происходит при n=3 N=23
=8,  . .
Чтобы передать код функции Уолша, необходимо три бита информации. (23
=8)
Первые 8 функций Уолша будут иметь следующий вид:
Структура группового сигнала
Рассмотрим формирование группового сигнала (рис. 9).
С помощью распределителя импульсов 8 датчиков опрашиваются поочередно. Максимальная  в этом случае будет, если в i-ом цикле опроса погрешность аппроксимации превысила допустимое значение в каком-то к-ом канале и остальные каналы “молчат”, а на i+1 цикле погрешность аппроксимации превысила допустимое значение в том же к-ом канале. Пусть срабатывание АВД произошло в 1-ом канале. Тогда сигнал с выхода АД (при вышеперечисленных условиях) будет иметь следующий вид: в этом случае будет, если в i-ом цикле опроса погрешность аппроксимации превысила допустимое значение в каком-то к-ом канале и остальные каналы “молчат”, а на i+1 цикле погрешность аппроксимации превысила допустимое значение в том же к-ом канале. Пусть срабатывание АВД произошло в 1-ом канале. Тогда сигнал с выхода АД (при вышеперечисленных условиях) будет иметь следующий вид:
где t1 - время необходимое для работы БС, t2 - время необходимое для опроса оставшихся датчиков.
Тогда t1+ t2=1/ . t2 определяется . t2 определяется  .Для нормальной работы устройства уплотнения по форме необходимо, чтобы битовая информация со схем АД поступала синхронно, а для этого надо, чтобы сдвиг сигналов со схем АД был кратен одному биту. Исходя из этого .Для нормальной работы устройства уплотнения по форме необходимо, чтобы битовая информация со схем АД поступала синхронно, а для этого надо, чтобы сдвиг сигналов со схем АД был кратен одному биту. Исходя из этого  ,где t ,где t - длительность синхросигнала , t - длительность синхросигнала , t - время необходимое для передачи информации с одного датчика. - время необходимое для передачи информации с одного датчика.
На вход устройства АД с датчиков (Д) поступает аналоговый сигнал. Так как мы используем адаптивную дискретизацию, необходимо вставить разделительные импульсы РИ для организации сообщений о времени. Разделительные сообщения о времени передаются при каждой значащей части сообщения. Синхросигнал будет выдаваться каждый цикл опроса 8 датчиков.
Так как на каждый АД поступает информация с 8 датчиков, то 23
=8 и вполне достаточно 3 бит адресной информации. Как было посчитано ранее на кодировку отсчета необходимо 5 бит. Разделительный импульс будет в виде одного бита единичного значения. Он необходим, чтобы на приемной стороне определить нахождение адреса и информации.
Будем называть сигнал с выхода АД информационным словом, то есть информационное слово = № датчика + информация.
Длина информационного слова 3+5=8 бит
.
Далее информационные слова со всех АД поступают на схему уплотнения по форме (рис.11).
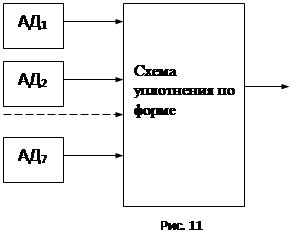
Каждый бит информационного слова модулирует по амплитуде базисную функцию, соответствующую номеру АД. Модуляция осуществляется умножителем. В результате выходное напряжение умножителей будет соответствовать форме базисной функции с соответствующей амплитудой. В данном случае, как уже отмечалось выше, каждая базисная функция (функция Уолша) содержит N=3 символа (бита). Соответственно длина информационного слова увеличится в  раз (3 раза). раз (3 раза).
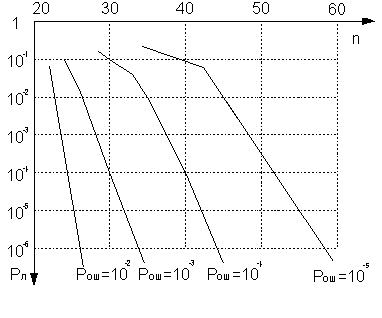
Далее сигналы со всех умножителей складываются по уровню, и к этой последовательности подмешивается синхрослово. Длина синхрослова рассчитывается исходя из вероятности ошибки на символ. По графику на рис.12 при вероятности ошибки на символ  и задаваясь вероятностью ложного обнаружения синхросигнала и задаваясь вероятностью ложного обнаружения синхросигнала , определяем длину синхросигнала , определяем длину синхросигнала  . В качестве синхрослова будем использовать М-последовательность, длина которой находится по формуле . В качестве синхрослова будем использовать М-последовательность, длина которой находится по формуле  . Соответственно в данном случае выберем длину синхрослова . Соответственно в данном случае выберем длину синхрослова  . .
 В итоге групповой сигнал с выхода схемы уплотнения примет вид
 … …
РИ – разделительный импульс (1 бит)
Длина группового сигнала N= 63+1+(8*3)=88 бит
.
Длительность группового сигнала определяется частотой опроса Tд
= 1/F0
= 1/46740=21,4мкс
Длительность передачи одного символа (бита): t = Tд
/N = 21,4*10-6
/88 = 244 нс
Соответственно частота тактового генератора: fT
=1/t = 1/244*10-9
= 4,1 МГц
Основные временные диаграммы системы
На рис.13 изображена общая структурная схема разрабатываемой системы сжатия и уплотнения по форме. На выходе системы уплотнения по форме сигналы с систем АД помножены на функцию Уолша. Сигналы с АД после схемы уплотнения по форме будут перемешаны, так что выделить в нем синхросигнал, адрес или информацию не возможно. Поэтому временные диаграммы покажем на выходе схем АД. На рис.14 показаны временные диаграммы в принципиально важных точках системы.
На рис.14, а показан аналоговый сигнал, поступающий из какого-то датчика (Д) на вход системы сжатия АД. После обработки в АД сигнал приобретает вид 14, б. Этот сигнал содержит информацию об адресе датчика, о данных с датчика. Затем сигналы с выходов АД параллельно поступают на вход системы уплотнения по форме. Там сигналы побитно умножаются на свои базисные функции в зависимости от номера АД, и суммируются.
Заключение
В данном проекте разработана система сжатия и уплотнения каналов, определены её основные параметры с учётом данных технического задания. Спроектированная система может использоваться как составная часть систем телеметрии или радионавигации. По сравнению с аналоговыми системами, данная цифровая система более стабильна в работе, обеспечивает передачу большего числа информации, обеспечивает лучшую точность передачи информации.
Список литературы
1. Кириллов С.Н., Стукалов Д.Н. Цифровые системы обработки речевых сигналов. Рязань, РРТИ, 1995 г.
2. Кириллов С.Н. Курс лекций по дисциплине «Основы теории сжатия информации и уплотнение каналов». Рязань, 2003 г.
3. Тепляков И.М., Рощин Б.В., Фомин А.И., Вейцель В.А. Радиосистемы передачи информации. М.,1982г.
4. Адаптивные телеизмерительные системы, под ред. А.Б. Фремке, М., 1981 г.
5. Левин, Плоткин, Цифровые системы передачи информации, 1982 г.
6. Рабинер Л.Р., Шафер Р.В., Цифровая обработка речевых сигналов. М., 1981 г.
7. Свиридов Н.Г. Проектирование РТС передачи информации. Рязань, РРТИ, 1988 г.
|