|
Химия и физика пленкообразующих веществ.
Контрольная работа №1
| Билет №13
|
| 1
|
—
|
Персистентная длина цепи.
|
| 2
|
—
|
Влияние концентрации полимера и термодинамического качества растворителя на вязкость концентрированных растворов.
|
| 3
|
—
|
Методы определения оптических свойств покрытий.
|
| |
|
|
| Билет №7
|
| 1
|
—
|
Ультрацентрифугирование.
|
| 2
|
—
|
Методы измерения вязкости жидкостей: капиллярная и ротационная вискозиметрия.
|
Билет №13.
1.
Персистентная длина цепи.
Персистентная длина цепи. Эта характеристика гибкости макромолекул основана на графическом анализе проекции полимерной цепи, образующей на плоскости линию с непрерывно изменяющейся кривизной («червеобразную» цепь) [рис.1].
Эта характеристика гибкости макромолекул была предложена Породом и Доти.
Проекция вектора расстояния между концами бесконечно длинной цепи  на направление касательной первому звену такой молекулы, равная на направление касательной первому звену такой молекулы, равная  , и соответствует персистентной длине. , и соответствует персистентной длине.
Персистентная длина в 2 раза меньше статистического сегмента Кулона, т.е.
 . .
Оценить значения  целесообразно для полужестких цепей, когда целесообразно для полужестких цепей, когда 
В этом случае:


Рис.1. Проекции цепи на плоскость для расчета:
а) размеров сегмента Куна; б) персистентной длины.
Билет №13.
2.
Влияние концентрации полимера и термодинамического качества растворителя на вязкость концентрированных растворов.
Смешение линейного или разветвленного полимера с низкомолекулярной жидкостью может привести либо к растворению, либо к образованию коллоидной системы – в зависимости от достигаемой степени дисперсности. При достижении молекулярной степени дисперсности образуются истинные растворы, для которых характерны самопроизвольность образования, равновестность, гомогенность, стабильность.
Системы полимер – растворитель
, концентрация полимера в которых такова, что взаимодействием между растворенными макромолекулами можно пренебречь, называются разбавленными растворами. Концентрационной границей является величина  . Макромолекулы в разбавленном растворе представляют собой более или менее анизотропные по форме статистические клубки, способные удерживать в результате сольватации или иммобилизации некоторое количество молекул растворителя. Свободное движение таких молекулярных клубков может быть уподоблено движению сферической частицы, радиус которой соответствует большой полуоси гипотетического эллипсоида вращения, а объем ее равен объему статистического клубка. Вязкость таких растворов описывается уравнением Энштейна: . Макромолекулы в разбавленном растворе представляют собой более или менее анизотропные по форме статистические клубки, способные удерживать в результате сольватации или иммобилизации некоторое количество молекул растворителя. Свободное движение таких молекулярных клубков может быть уподоблено движению сферической частицы, радиус которой соответствует большой полуоси гипотетического эллипсоида вращения, а объем ее равен объему статистического клубка. Вязкость таких растворов описывается уравнением Энштейна:
здесь  - коэффициент формы; для сферической частицы - коэффициент формы; для сферической частицы  , для клубков анизотропной формы: , для клубков анизотропной формы: 
где a
и b
– большая и малая полуоси гипотетического эллипсоида вращения молекулярного клубка, - объемная доля полимера. - объемная доля полимера.
Закон Эйнштейна выполняется достаточно строго лишь до концентрации  . .
Однако асимметрия молекулярных клубков является причиной проявления аномалии вязкостных свойств даже в разбавленных растворах синтетических и природных полимеров вследствие ориентации таких частиц в потоке при достаточно больших τ, а также из-за гидродинамического взаимодействия. При небольших и средних τ разбавленные растворы полимеров являются ньютоновскими жидкостями.
Растворы полимеров, в которых отсутствует линейность концентрационной зависимости вязкости, называются концентрированными.
Резкое увеличение вязкости концентрированных растворов с повышением концентрации полимера объясняется следующими структурными и термодинамическими факторами:
Увеличение концентрации полимера приводит к возрастанию вязкости растворов полимеров в тем большей степени, чем:
- хуже термодинамическое качество растворителя
- больше молекулярная масса полимера
- шире молекулярно-массовое распределение (при  ) )
- жестче полимерные цепи
- ниже температура раствора.
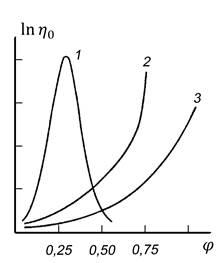
Рис. 2.1 Влияние концентрации полимеров ( φ – объемная доля полимеров) на эффективную вязкость концентрированных растворов полимеров:
1 – жесткоцепные полимеры (

2 – полужесткоцепные полимеры
3 – гибкоцепные полимеры (

Следует отметить неопределенность понятия «концентрированный раствор полимера», тем более что граничное условие  тоже приблизительно. тоже приблизительно.
Например, Дж. Ферри относит к концентрированным также растворы полимеров, в которых отношение вязкости раствора к вязкости растворителя, т.е. больше 100. В зависимости от термодинамической гибкости макромолекул область перехода от разбавленных к концентрированным растворам составляет от долей % (мас.) – для жесткоцепных до 8-10% (мас.) – для гибкоцепных полимеров.
Условно принимают, что к среднеконцентрированным растворам можно отнести растворы, содержащие до 0,3 объемных долей полимера, с бо’льшим содержанием полимера – к высококонцентрированным. Влияние концентрации полимеров на вязкость неразрушенной структуры растворов полимеров различной гибкости иллюстрируется на [рис.2.1]. Возрастание  при увеличении концентрации происходит тем интенсивней, чем более жестки макромолекулы. при увеличении концентрации происходит тем интенсивней, чем более жестки макромолекулы.
Концентрационная зависимость  существенно зависит от доли свободного объема системы. Согласно Фуджите – Касимото, существенно зависит от доли свободного объема системы. Согласно Фуджите – Касимото,

где:

Здесь  и и  - вязкость растворов с объемными долями растворителя - вязкость растворов с объемными долями растворителя  и и  при температуре Т
, причем второй раствор ( при температуре Т
, причем второй раствор ( выбран в качестве стандартного; выбран в качестве стандартного;  - доля свободного объема стандартного раствора; - доля свободного объема стандартного раствора;  - функция взаимодействия полимера с растворителем. - функция взаимодействия полимера с растворителем.
Зависимость  или или  описывается также уравнением Келли – Бики: описывается также уравнением Келли – Бики:

где  - объемная доля полимера в растворе; - объемная доля полимера в растворе;  - параметр, включающий молекулярную массу полимера; - параметр, включающий молекулярную массу полимера;  - плотность раствора; - плотность раствора;  - температура раствора; - температура раствора;  и и  - температуры стеклования полимера в твердом состоянии и в растворе соответственно; - температуры стеклования полимера в твердом состоянии и в растворе соответственно;  - температурный коэффициент свободного объема - температурный коэффициент свободного объема  . .
Для полимеров обычно принимают  , ,
т.е.  , так как , так как  при при 
Для раствора  , причем , причем 
Концентрационная зависимость вязкости растворов полимеров в первом приближении может быть описана следующими соотношениями:
по Я. Франкелю – 
по С. Папкову – 
где А
и В
– постоянные для данной системы «полимер – растворитель»; С
– концентрация полимера (по массе).
Для ряда волокнообразующих полимеров (ХПВХ, ПАН, АЦ) может быть принято полулогарифмическое соотношение в области средних концентраций:

В этом случае значения постоянных А и В существенно зависят от термодинамического качества растворителя [рис.2.2]: его ухудшение обусловливает более резкое увеличение  . Эти результаты свидетельствуют о том, что вязкость изоконцентрированных растворов тем ниже, чем лучше термодинамические свойства растворителя. . Эти результаты свидетельствуют о том, что вязкость изоконцентрированных растворов тем ниже, чем лучше термодинамические свойства растворителя.
Очевидно, что уравнения и и  описывают соответствующие прямолинейные зависимости, что позволяет проводить расчетную оценку вязкостных свойств при различных концентрациях растворов. описывают соответствующие прямолинейные зависимости, что позволяет проводить расчетную оценку вязкостных свойств при различных концентрациях растворов.
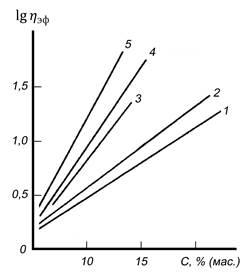
Рис. 2.2. Влияние природы растворителя на эффективную вязкость концентрированных растворов полиакрилонитрила ( С – концентрация полимера) при 298 К и τ = 5 Па.
Растворители:
1 - диметилформамид;
2 - диметилсульфоксид;
3 - 90% -й водный раствор этиленкарбоната;
4 - 51,5% -й водный раствор
NaCNS
;
5 - 60% -й водный раствор
ZnCl
2
.
Билет №13
.
3.
Методы определения оптических свойств покрытий.
Оптические свойства. К оптическим характеристикам покрытий относятся:
- Цвет
- Прозрачность
- Укрывистость
- Блеск.
Эти свойства определяются составом и качеством приготовления лакокрасочного материала, природой и качеством подготовки поверхности, соблюдением технологического формирования покрытия. При оценке внешнего вида покрытий необходимо учитывать их функциональное назначение, физиологическое и психологическое влияние на человека. Оптические свойства, как и другие показатели покрытий, изменятся в процессе эксплуатации, поэтому необходимое требование к покрытиям – их длительная стабильность.
Для определения оптических свойств покрытий применяют:
- Спектрофотометрический
- Колориметрический
- Визуальный способы.
Спектрофотометрический метод
основан на определении спектрального состава излучения, спектральных коэффициентов пропускания и отражения, яркости образцов, отражающих свет.
Измерение колориметрическим методом
основано на принципе смешения окрашенных световых потоков с известными параметрами (или смешения цветов), при котором достигается идентификация определяемого цвета.
Для каждой области спектра преимущественно используют свои приборы. Так, для характеристики пленок и покрытий в видимой области применяют спектрофотометр СФ-18, фотометры ФО-1, ФОУ, колориметры фотоэлектрические КФО и КФК-2, КФК-3 [рис.3] и т.д.
Более широкий диапазон измерений, включая видимую и УФ-области, имеют  спектрофотометры СФ-20 и СФ-26 и фотометры ФМ-59, ФМ-85 и ФМ-99. Последние два прибора работают и в ближней ИК-области. Однако для ИК-области применяют в основном специальные приборы — спектрометры ИКС-29 и ИКС-31. Для определения коэффициента излучения 8 непрозрачных материалов пользуются терморадиометрами ТИС, ТРМ-И и тепловизором АГА-680, а коэффициента поглощения солнечного излучения cxs — альбедометром М-69. спектрофотометры СФ-20 и СФ-26 и фотометры ФМ-59, ФМ-85 и ФМ-99. Последние два прибора работают и в ближней ИК-области. Однако для ИК-области применяют в основном специальные приборы — спектрометры ИКС-29 и ИКС-31. Для определения коэффициента излучения 8 непрозрачных материалов пользуются терморадиометрами ТИС, ТРМ-И и тепловизором АГА-680, а коэффициента поглощения солнечного излучения cxs — альбедометром М-69.
Рис.3. Колориметр фотоэлектрический КФК-3.
Для инструментальной оценки цвета покрытий служат фильтровой колориметр ФМ-104м и компаратор цвета КЦ-2, оснащенный микро-ЭВМ.
Визуальный метод
определения цвета связан со сравнением испытываемых образцов с эталонными накрасками картотеки или атласа цветовых эталонов. Имеются картотеки, разработанные в ГИПИ ЛКП и во ВНИИ технической эстетики, а также атласы цветов.
Блеск покрытий
определяют с помощью фотоэлектрических блескомеров ФБ-2 [рис. 4] и ФБ-5.
Блескомер предназначен для измерения коэффициента зеркального отображения (при геометрии освещения-наблюдения 45°/45°) и коэффициента яркости (при 45°/0°) направленного светового потока от поверхности лакокрасочных покрытий в видимой области спектра с целью количественной оценки зрительного восприятия человеческим глазом степени блеска (ГОСТ 896-69) и белизны указанных покрытий.
Определение основано на измерении фототока, возникающего под действием пучка света, падающего на поверхность покрытия под углом 45⁰ и отраженного от нее.
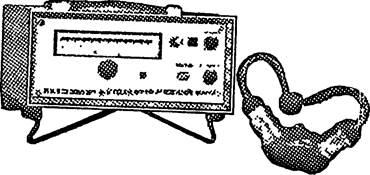
Рис. 4. Блескомер типа ФБ-2.
Билет №7.
1.
Ультрацентрифугирование.
Ультрацентрифугирование -
метод разделения и исследования частиц размером менее 100 нм (макромолекул органелл животных и растительных клеток, вирусов и др.) в поле центробежных сил. Позволяет разделять смеси частиц на фракции или индивидуальные компоненты, находить молекулярную массу и ММР полимеров, плотность их сельватов. Дает возможность оценивать форму и размеры макромолекул в растворе, влияние статического давления на стабильность частиц, параметры взаимодействия типа ассоциация - диссоциация макромолекул друг с другом или с молекулами низкомолекулярных компонентов и ионами, влияние природы растворителя на конформации макромолекул и др.
Метод осуществляется с помощью ультрацентрифуг. Ультрацентрифуга
(от ультра
..., центр
и лат. fugo — бег, бегство), прибор для разделения частиц менее 100 нм (коллоидов, субклеточных частиц, макромолекул белков, нуклеиновых кислот, липидов, полисахаридов, синтетических полимеров и пр.), взвешенных или растворённых в жидкости; это достигается вращением ротора, создающего центробежное поле с ускорением, на много порядков превышающим ускорение силы тяжести.
Первая ультрацентрифуга, предназначенная для изучения движения частиц, невидимых в световой микроскоп, была создана шведским учёным - химиком Теодором Сведбергом (Theodor Swedberg, 1884-1971) в 1923 (публикация в 1924). В этой ультрацентрифуге достигались центробежные ускорения всего до 5000 g. Она имела абсорбционную оптическую систему и использовалась для изучения движения частиц золота диаметром около 5 нм. В 1926 Т.Сведберг сконструировал первую высокоскоростную ультрацентрифугу (41000 об/мин, ускорения — до 105
g), с помощью которой проводились аналитические исследования белков в растворах (в частности, гемоглобина). В 1939 Т.Сведбергом создана аналитическая ультрацентрифуга со стальным ротором (65000 об/мин).
По назначению и конструкции ультрацентрифуги подразделяются на:
- препаративные,
- аналитические
- препаративно-аналитические.
Препаративные ультрацентрифуги
снабжены угловыми роторами с гнёздами для цилиндрических пробирок, стаканов или бутылок, наклоненных под углом 20 – 40° к вертикальной оси ротора, либо так называемыми бакетными роторами со стаканами, поворачивающимися на 90° при вращении. Существуют также зональные и проточные роторы с одной большой внутренней полостью для фракционируемой жидкости. Данные ультрацентрифуги используются для выделения отдельных компонентов из сложных смесей.
Аналитические ультрацентрифуги
снабжены роторами со сквозными цилиндрическими гнёздами, в которые помещены специальные прозрачные кюветы для исследуемых растворов или суспензий. Процесс перераспределения частиц в них можно наблюдать непосредственно при вращении ротора с помощью специальных оптических систем (рефрактометрических, абсорбционных). Существуют модели аналитических ультрацентрифуг, соединённых с ЭВМ, производящими автоматическую обработку экспериментальных данных.
Ультрацентрифугирование подразделяется на:
- скоростное
- равновесное.
В первом случае частицы движутся по радиусу ротора соотв. своим коэф. седиментации, в первом приближении пропорциональным массе частицы, разности плотностей частицы и жидкости и жидкости при при  частицы перемещаются от оси вращения ротора к периферии (седиментируют), при частицы перемещаются от оси вращения ротора к периферии (седиментируют), при  - в сторону оси вращения (флотируют). - в сторону оси вращения (флотируют).
При равновесном ультрацентрифугировании перенос частиц по радиусу продолжается до тех пор, пока сумма химического потенциала и молярной потенциальной энергии в каждой точке системы не станет постоянной величиной, после чего распределение частиц перестанет изменяться.
Билет №7.
2.
Методы измерения вязкости жидкостей: капиллярная и ротационная вискозиметрия.
Вязкость жидкостей (внутреннее трение) - свойство оказывать сопротивление перемещению одной их части относительно другой.
Вискозиметры (от латинского «viscous» - вязкость) – приборы для измерения вязкости – в настоящее время широко применяются в различных областях науки, техники и промышленности.
По принципу работы существующие модели вискозиметров делят на четыре основные группы: капиллярные, ротационные, с падающим шариком, вибрационные.

Вискозиметры – достаточно дорогостоящие приборы. Большинство существующих моделей вискозиметров для измерений требуют сравнительно большие объемы жидкостей (100 и более мл), что не всегда возможно, например, при исследовании дорогих или токсичных жидкостей, а также при реологическом анализе крови. Кроме того, промышленно выпускаемые модели имеют не очень широкий диапазон измерений; внешние условия могут влиять на результаты эксперимента, а переградуировка приборов трудоемка.
Метод капиллярной вискозиметрии.
Метод капиллярной вискозиметрии опирается на закон Пуазейля о вязкой жидкости, описывающий закономерности движения жидкости в капилляре.
Приведем уравнение гидродинамики для стационарного течения жидкости, с вязкостью  через капилляр вискозиметра: через капилляр вискозиметра:


Q
– количество жидкости, протекающей через капилляр капиллярного вискозиметра в единицу времени, м3
/с,
R
– радиус капилляра вискозиметра, м
L
– длина капилляра капиллярного вискозиметра, м
 – вязкость жидкости, Па·с, – вязкость жидкости, Па·с,
p
– разность давлений на концах капилляра вискозиметра, Па.
Отметим, что формула Пуазейля справедлива только для ламинарного потока жидкости, то есть при отсутствии скольжения на границе «жидкость – стенка капилляра вискозиметра».
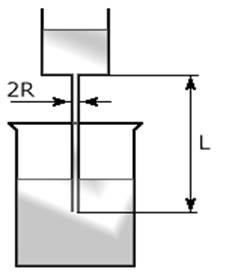 Приведенное уравнение используют для определения динамической вязкости. Ниже [рис.5] размещено схематическое изображение капиллярного вискозиметра. Приведенное уравнение используют для определения динамической вязкости. Ниже [рис.5] размещено схематическое изображение капиллярного вискозиметра.
В капиллярном вискозиметре жидкость из одного сосуда под влиянием разности давлений р
истекает через капилляр сечения 2R
и длины L
в другой сосуд. Из рисунка видно, что сосуды имеют во много раз большее поперечное сечение, чем капилляр вискозиметра, и соответственно этому скорость движения жидкости в обоих сосудах в N
раз меньше, чем в капилляре вискозиметра. Таким образом не все давление пойдет на преодоление вязкого сопротивления жидкости, очевидно, что часть его будет расходоваться на сообщение жидкости неопределённой кинетической энергии. Следовательно, в уравнение Пуазейля необходимо ввести некоторую поправку на кинетическую энергию, называемую поправкой Хагенбаха:
| Рис. 5. Схематическое изображение капиллярного вискозиметра
|

где h
– коэффициент, стремящийся к единице,
d
– плотность исследуемой жидкости.
|
Вторую поправку условно назовём поправкой влияния начального участка капилляра вискозиметра на характер движения исследуемой жидкости. Она будет характеризовать возможное возникновение винтового движения и завихрения в месте сопряжения капилляра с резервуаром капиллярного вискозиметра (откуда вытекает жидкость). Суть поправки состоит в том, что вместо истинной длины капилляра вискозиметра L
мы вводим кажущуюся длину L':

n
– определяется экспериментально на основе изменений при разных значениях L
и примерно равен единице 
Следует учитывать, что при измерении вязкости органических жидкостей с большой кинематической вязкостью поправка Хагенбаха незначительна и составляет доли процента. Если же говорить о высокотемпературных вискозиметрах, то вследствие малой кинематической вязкости жидких металлов поправка может достигать 15%.
Метод капиллярной вискозиметрии вполне можно отнести к высокоточному методу вискозиметрии в силу того, что относительная погрешность измерений составляет доли процента, в зависимости от подбора материалов вискозиметра и точности отсчёта времени, а также иных параметров, участвующих в методе капиллярного истечения.
Ротационный метод.
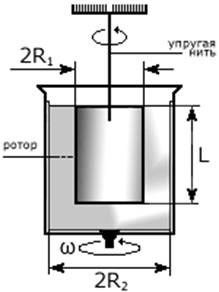 Ротационный метод вискозиметрии заключается в том, что исследуемая жидкость помещается в малый зазор между двумя телами, необходимый для сдвига исследуемой среды. Одно из тел на протяжении всего опыта остаётся неподвижным, другое, называемое ротором ротационного вискозиметра, совершает вращение с постоянной скоростью. Очевидно, что вращательное движение ротора визкозиметра передается к другой поверхности (посредством движения вязкой среды; отсутствие проскальзывания среды у поверхностей тела предполагается, таким образом рассматриваются). Отсюда следует тезис: момент вращения ротора ротационного вискозиметра является мерой вязкости. Ротационный метод вискозиметрии заключается в том, что исследуемая жидкость помещается в малый зазор между двумя телами, необходимый для сдвига исследуемой среды. Одно из тел на протяжении всего опыта остаётся неподвижным, другое, называемое ротором ротационного вискозиметра, совершает вращение с постоянной скоростью. Очевидно, что вращательное движение ротора визкозиметра передается к другой поверхности (посредством движения вязкой среды; отсутствие проскальзывания среды у поверхностей тела предполагается, таким образом рассматриваются). Отсюда следует тезис: момент вращения ротора ротационного вискозиметра является мерой вязкости.
Для простоты мы рассмотрим инверсную модель ротационного вискозиметра [рис. 6]: вращаться будет внешнее тело, внутреннее тело останется неподвижным, ему и будет сообщаться момент вращения. Однако для краткости изложения будем называть внутреннее тело ротором ротационного вискозиметра.
Рис. 6. Схематическое изображение
ротационного вискозиметра.
Введём необходимые обозначения:
| R1
,L
|

|
радиус и длина ротора ротационного вискозиметра
|
| ω
|

|
постоянная угловая скорость вращения внешнего тела
|
| R2
|

|
радиус вращающегося резервуара ротационного вискозиметра
|
| η
|

|
вязкость исследуемой cреды
|
| M1
|

|
момент вращения, передаваемый через вязкую жидкость, равный

|
| d, l
|

|
диаметр и длина упругой нити
|
| φ
|

|
угол, на который закручивается неподвижно закреплённая нить,
|
| G
|

|
момент упругости материала нити
|
При этом крутящий момент M1
ротора ротационного вискозиметра уравновешивается моментом сил упругости нити М2
:

Заметим вновь, что М1
= М2
, откуда после нескольких преобразований относительно η
имеем:

или  где k
– постоянная ротационного вискозиметра. где k
– постоянная ротационного вискозиметра.
| Литература:
|
| 1.
|
Боуэн Т., Введение в ультрацентрифугирование, пер. с англ., М., 1973.
(первоисточник – Schachman Н. К., Ultra centrifugation in biochemistry, - L., 1959).
|
| 2.
|
Бурдун Г.Д., Марков Б.Н. Основы метрологии, М., 1972.
|
| 3.
|
Геллер Б. Э., Геллер А. А., Чиртулов В. Г. Практическое руководство по физикохимии волокнообразующих полимеров. Учебное пособие для вузов, 2-ое изд., исправл. доп.,
М.: «Химия», 1996, 432 с.: ил.
|
| 4.
|
Лотц Ю. А., Ожерельев А, Я., Аналитическая ультрацентрифуга, «Уникальные приборы», 1970, № 5. (Svedderg Т., Pedersen K. O., The Ultracentrifuge, Oxf., 1940).
|
| 5.
|
Химия и технология пленкообразующих веществ: Учебное пособие для студентов вузов / Н. Р. Прокопчук, Э. Т. Крутько. – Мн.: БГТУ, 2004. – 423 с.: ил.
|
| 6.
|
Химия и технология лакокрасочных материалов и покрытий: Учебное пособие для студентов вузов / Э. Т. Крутько, Н. Р. Прокопчук. – Мн.: БГТУ, 2004. – 314 с.
|
| |
|
| Интернет – источники:
|
| |
| 1.
|
http:// www.bse.sci-lib.com
|
—
|
Химия в Большой Научной Библиотеке. Большая Советская Энциклопедия. Ультрацентрифугирование.
|
| 2.
|
http://www.measurement.ru
|
—
|
машины и приборы для испытания полимерных материалов. Блескомер фотоэлектрический типа ФБ-2.
|
| 3.
|
http:// www.mechanician.ru
|
—
|
лакокрасочные материалы. Оптические свойства.
|
| 4.
|
http://www.slav-med.ru
|
—
|
оборудование. Фотоколориметры.
|
| 5.
|
http://www.ximuk.ru
|
—
|
Сайт о химии. Ультрацентрифугирование.
|
|