Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа
По дисциплине: Физика
Новосибирск, 2009
ВАРИАНТ 3
503. Точка совершает простые гармонические колебания, уравнение которых X= Asin wt, где А=5 см, w=2с-1
. В момент времени, когда точка обладала потенциальной энергией П=0,1 мДж, на нее действовала возвращающая сила F=5 мН. Найти этот момент времени t.
Решение:
Воспользуемся Законом сохранения энергии для данной системы:
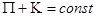 , где , где 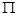 – потенциальная энергия – потенциальная энергия
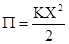 , где , где 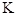 - коэффициент жесткости системы - коэффициент жесткости системы
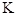 - кинетическая энергия, равная - кинетическая энергия, равная  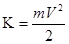 , где , где 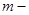 масса тела, масса тела,
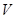 - скорость тела - скорость тела
Возьмем производную от 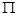 по по 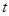 ( (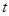 – время) – время)
 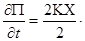 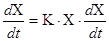 
 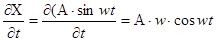
С другой стороны из соотношения 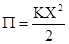 получаем: получаем:
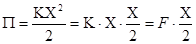 где где 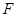 - возвращающая сила, получаем: - возвращающая сила, получаем:
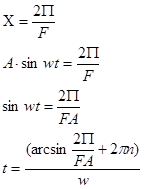
где 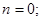 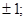 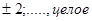
Размерность  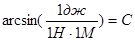
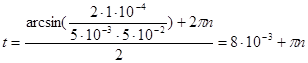 раз. раз. 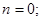 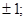 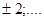
Ответ: В момент времени 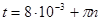 ( (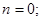 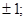 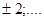 ) )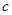
513. В электрическом контуре изменение тока описывается уравнением: 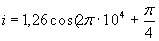 ), A. Записать уравнение колебаний заряда на конденсаторе, определить период колебаний. ), A. Записать уравнение колебаний заряда на конденсаторе, определить период колебаний.
Решение:
Скорее всего, в условии задачи допущена ошибка и изменение тока описывается уравнением:
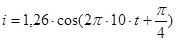 А (пропущено время t) А (пропущено время t)
По определению тока:
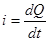
получаем выражение для заряда
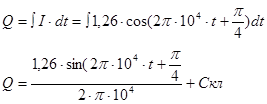
где С – константа, определяемая из начальных условий. Таким образом получаем:
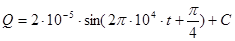
период колебаний найдем из соотношения:
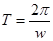 где где 
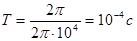
Ответ: уравнение колебаний заряда на конденсаторе:
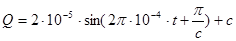 (с-константа) Кл (с-константа) Кл
период 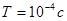
523. Материальная точка участвует одновременно в двух взаимно-перпендикулярных колебаниях, происходящих согласно уравнениям: 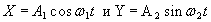 . A1
=3 cм, А2
=2 см, ω1
=1 с-1
, ω2
=1 с-1
. Определить траекторию точки. Построить траекторию с соблюдением масштаба, указать направление движения точки. . A1
=3 cм, А2
=2 см, ω1
=1 с-1
, ω2
=1 с-1
. Определить траекторию точки. Построить траекторию с соблюдением масштаба, указать направление движения точки.
Решение:
Поскольку  , то запишем наше уравнение движения, используя математическое равенство: , то запишем наше уравнение движения, используя математическое равенство:
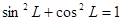
в виде: 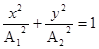
Это есть уравнение Эллипса, с центром Эллипса вначале координат, и полуосями по координате x равной А, по координате 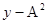
Сделаем чертеж. Направление движения точки против часовой стрелки поскольку в начальный момент при 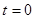 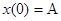 ; ; 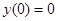 , при очень маленьком , при очень маленьком 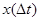 ставится немного меньше ставится немного меньше 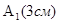 , а , а 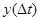 немного увеличивается, значит, движение осуществляется на графике против часовой стрелки. немного увеличивается, значит, движение осуществляется на графике против часовой стрелки.
          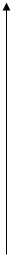  Y Y
2 см

 1 1
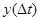
  1 2 3 1 2 3
0 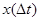 x x
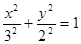
533. Колебательный контур имеет конденсатор емкостью 0,2 мкФ, катушку индуктивности 5 мГн и резистор. При каком логарифмическом декременте затухания разность потенциалов на обкладках конденсатора уменьшится за 1 мс в три раза? Чему равно при этом сопротивление резистора?
Решение: Логарифмический декремент затухания:
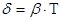
где 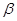 - коэффициент затухания, равный: - коэффициент затухания, равный:
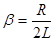
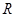 - сопротивление контура; - сопротивление контура;
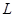 - индуктивность контура; - индуктивность контура;
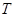 – период колебания системы, – период колебания системы, 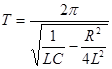
Логарифмический декремент затухания показывает, во сколько раз изменится логарифм амплитуды двух последовательных колебаний:
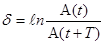
Уравнение, описывающее изменение напряжения на обкладках конденсатора имеют вид: 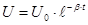
где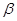 – коэффициент затухания – коэффициент затухания
тогда
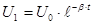
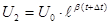
По условию задачи  за время за время 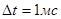

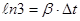
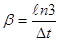
Период колебаний можно определить по формуле:
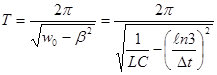
где 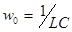 – собственная частота колебаний контура. – собственная частота колебаний контура.
Тогда логарифмический декремент затуханий равен:
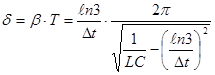
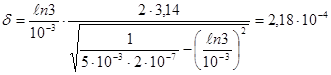
Сопротивление резистора найдем из соотношения
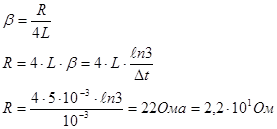
Ответ: логарифмический декремент затухания 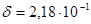
Сопротивление резистора 
543. Уравнение незатухающих звуковых колебаний дано в виде: Y = 10cos0,5t, см. Написать уравнение волны, если скорость распространения колебаний 340 м/с, 2). Найти смещение точки, отстоящей на расстоянии 680 м от источника колебаний, через две секунды от начала колебаний.
Решение:
1) Уравнение волны имеет вид 
Где  - амплитуда колебания волны - амплитуда колебания волны
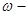 угловая частота угловая частота
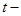 время, в которое мы определяем параметры волны время, в которое мы определяем параметры волны
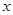 – расстояние от точки отсчета начала координат – расстояние от точки отсчета начала координат
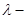 начальная фаза колебаний волны начальная фаза колебаний волны
Из условия задачи уравнение волны имеет вид:
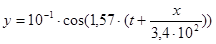 м м
2) Найдем смещение точки, подставив в уравнение волны наши параметры:
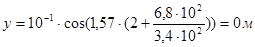
Ответ: 1) уравнение волны  м м
2) смещение точки 
603. Расстояние L
от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной l
= 1 см укладывается N =
10 темных интерференционных полос. Длина волны λ = 0,7 мкм.
Решение: Расстояние между двумя соседними максимумами в опыте Юнга равно (аналогично для минимумов – темных интерференционных полос):
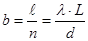 или или 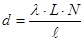
где  – длина волны света – длина волны света
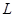 - расстояние от щелей до экрана - расстояние от щелей до экрана
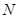 - число темных интерференционных полос на длине - число темных интерференционных полос на длине 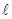 экрана. экрана.
Размерность 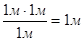
Подставим значение: 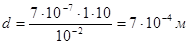
Ответ: 
613. На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница (λ = 780 нм) спектра третьего порядка?
Уравнение дифракции на дифракционной решетке выглядит как:
 (1) (1)
где 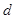 – постоянная решетки, – постоянная решетки, 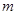 – порядок спектра, – порядок спектра,  – длина волны света; – длина волны света; 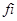 – угол отклонения дифрагированного луча от его первоначального направления. – угол отклонения дифрагированного луча от его первоначального направления.
Если две спектральные линии накладываются, значит они наблюдаются под одним углом 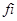 , а значит, левые части уравнения (1) для них одинаковы; отличаются же порядки и длины волн, т.е. для первой линии имеем: , а значит, левые части уравнения (1) для них одинаковы; отличаются же порядки и длины волн, т.е. для первой линии имеем:
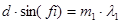 (2) (2)
где 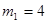 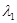 – искомая длина волны; для второй линии: – искомая длина волны; для второй линии:
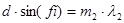 (3) (3)
где 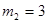 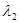 =780 нм. =780 нм.
Приравнивая правые части (2) и (3) выражаем 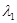 : :
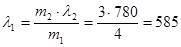 нм нм
623. Кварцевую пластинку поместили между скрещенными николями. При какой наименьшей толщине dmin
кварцевой пластины поле зрения между николями будет максимально просветлено? Постоянная вращения α кварца равна 27 град/мм.
Если бы пластинки не было, свет через два скрещенных поляризатора – николя не прошел бы. Однако пластинка из оптически активного материала способна поворачивать плоскость поляризации. Чтобы свет максимально прошел через второй поляризатор, нужно повернуть плоскость поляризации на 90 градусов, чтобы новая поляризация совпала с осью второго поляризатора. Формула для поворота плоскости поляризации:

где  град/мм, град/мм, 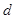 – искомая толщина пластинки: – искомая толщина пластинки:
 -> -> 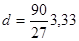 мм мм
|