СОДЕРЖАНИЕ
Лабораторная работа №1. Анализ САУ с помощью ЭВМ и программного обеспечения MATLAB/Simulink
Цель работы
Программа работы
Ход работы
1. Построение временных характеристик САУ с помощью пакета ControlSystem
2. Построение временных характеристик
3. Сборка модели системы в Simulink и построение ее переходной характеристики
4. Построение частотных характеристик САУ
5. Преобразование модели Simulink в модель ControlSystemMATLAB
Выводы
Лабораторная работа №2. Исследование устойчивости линейных САУ
Цель работы
Программа работы
Ход работы
1. Реализация системы
2. Проверка устойчивости системы по критерию Гурвица
3. Определение устойчивости системы по корням характеристического уравнения
4. Определение назначения функций ltiview
и margin
. Получение с их помощью информации о переходной характеристике и запасе устойчивости системы
6. Проверка системы на устойчивость по критерию Михайлова
7. Проверка системы на устойчивость согласно критерию Найквиста
Выводы
Лабораторная работа №3. Исследование многоконтурной системы автоматического регулирования
Цель работы
Программа работы
Ход работы
1. Реализация модели "жесткого" спутника Земли в Simulink
2. Охват модели ЖСЗ обратной связью по положению.
3. Охват модели ЖСЗ обратной связью по скорости и по положению.
4. Оценка влияния изменения коэффициента обратной связи по скорости на переходную характеристику системы.
5. Определение коэффициентов обратных связей САУ при известном времени окончания переходного процесса
6. Система с чистым запаздыванием. Оценка динамических свойств системы с различными временами задержки
Выводы
Лабораторная работа №1. Анализ САУ с помощью ЭВМ и программного обеспечения
MATLAB
/
Simulink
Воспользовавшись математическим программным обеспечением MATLAB и пакетом Simulink, исследовать систему автоматического управления (САУ).
1. Построить временные характеристики САУ с помощью пакета ControlSystem.
· Задать описание системы, имеющую передаточную функцию вида:
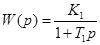 (1) (1)
с помощью функции tf
, если 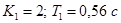 . .
· Задать описание системы (1) в виде нулей, полюсов и коэффициента передачи с помощью функции zpk
.
· Задать описание системы (1) в пространстве состояний с помощью функции ss
.
2. Построить временные характеристики:
· переходную – с помощью функции step
;
· импульсную (весовую) – с помощью функции impulse
.
3. Собрать модель системы в Simulink и определить переходную характеристику САУ.
4. Построить частотные характеристики САУ с помощью пакета ControlSystem, используя функции bode
и nyquist
.
5. Преобразование модели Simulink в модель ControlSystemMATLAB.
· Создать структурную схему в Simulink.
· Извлечь информацию из модели с помощью функции linmod
.
· Преобразовать матрицу состояния в модель ControlSystem.
1. Построение временных характеристик САУ с помощью пакета
ControlSystem
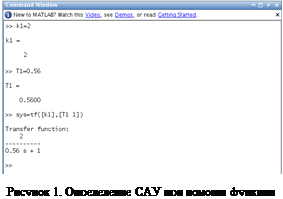
На рисунке 1. представлен фрагмент командного окна MATLAB, на котором изображено определение коэффициента передачи системы K
1
и постоянной времени T
1
и задание специальной переменной sys
, содержащей описание системы (1), при помощи функции tf
.
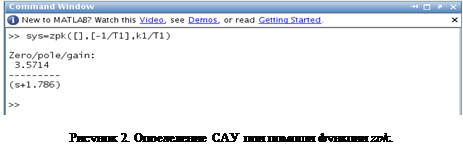
На рисунке 2. представлен фрагмент командного окна MATLAB, на котором изображен процесс задания описания системы (1) в виде нулей, полюсов и коэффициента передачи при помощи функции zpk
.
На рисунке 3 представлен фрагмент командного окна MATLAB, на котором изображен процесс задания описания системы (1) в пространстве состояний при помощи функции ss
. Результатом является специальная переменная описания системы sys
и матрицы состояний a
,b
,c
,d
.
2. Построение временных характеристик
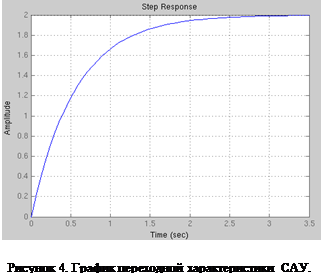
На рисунке 4 изображен график переходной характеристики системы (1), построенный при наличии специальной переменной описания системы sys
и функции step
.
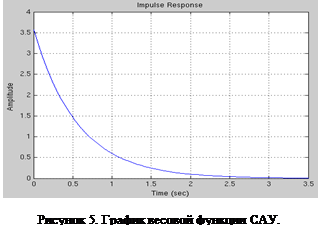
На рисунке 5 изображен график весовой функции системы (1), построенный при наличии специальной переменной описания системы sys
и функции impulse
.

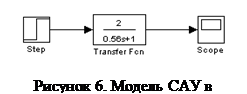
3. Сборка модели системы в Simulink и построение ее переходной характеристики
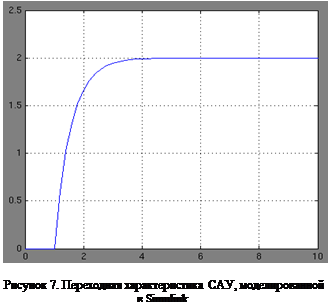
На рисунке 6 изображена модельная структура системы (1) для пакета Simulink. На рисунке 7 представлен график переходной функции системы (1),
как результат отображения блока Scope
на интервале 10 с.
4. Построение частотных характеристик САУ
На рисунке 8 изображены графические зависимости амплитуды децибелах и фазы в градусах входного сигнала от частоты в логарифмическом масштабе (диаграммы Боде) для заданной САУ. ЛАЧХ и ЛФЧХ системы построены при помощи функции bode
.
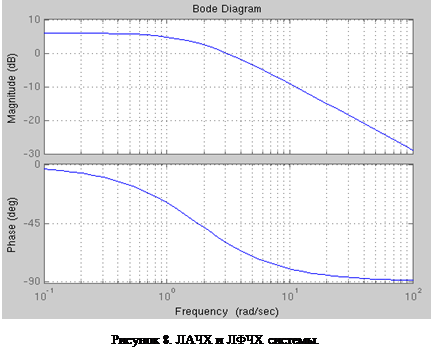
\
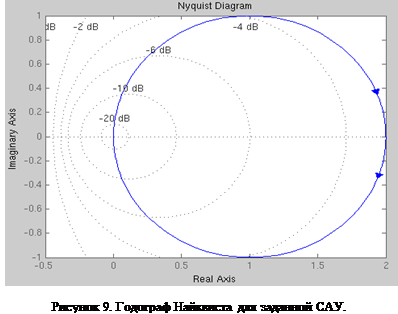
На рисунке 9 изображен график амплитудно-фазовой характеристики (годограф Найквиста) заданной САУ, построенный при помощи функции nyquist
.
5. Преобразование модели
Simulink в модель ControlSystemMATLAB
На рисунке 10. изображен структура системы в среде Simulink, предназначенная для извлечения из нее матриц состояния для манипуляций с САУ в ControlSystemMATLAB.

На рисунке 11 представлен фрагмент командного окна MATLAB, на котором изображен процесс извлечения матриц состояния системы при помощи функции linmod
.
На рисунке 12. представлен фрагмент командного окна MATLAB, на котором изображен процесс получения переменной описания системы в пространстве состояний при помощи функции sys
.


Полученная после преобразования модель может применяться для исследования САУ и построения ее временных и частотных характеристик при помощи функций step
, impulse
, bode
, nyquist
.
В работе ознакомились с основными функциональными средствами ПО MATLAB, пакета ControlSystem и среды численного моделирования структур САУ – Simulink.
Выполненная работа показала эффективность использования среды универсального моделирования MATLAB для определения характеристик систем автоматического управления.
Как видно из п.п. 1, описание системы можно представлять различными способами, что характеризует гибкость применяемого программного обеспечения.
Как видно из п.п. 3 и 5, в сочетании с пакетом Simulink, программный комплекс MATLAB является мощным средством для высокоточного цифрового моделирования САУ.
Исследовать замкнутую систему автоматического управления (ЗСАУ) при помощи критериев устойчивости Гурвица, Михайлова и Найквиста. Применить в работе ПО MATLAB.
Программа работы
1. Реализовать систему согласно следующим данным:
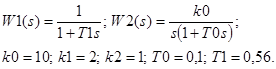
Структурная схема системы представлена на рисунке 1.
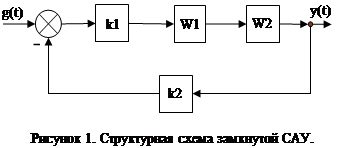
2. Проверить систему на устойчивость по алгебраическому критерию Гурвица. Сделать выводы.
3. Определить устойчивость системы по корням. Сделать выводы.
4. Изучить в MATLABHelp функции ltiview
и margin
и с их помощью получить информацию о переходной характеристике и оценить запас устойчивости.
5. Проверить систему на устойчивость по частотному критерию Михайлова. Сделать выводы.
6. Проверить систему на устойчивость по частотному критерию Найквиста. Сделать выводы.
1. Реализация системы
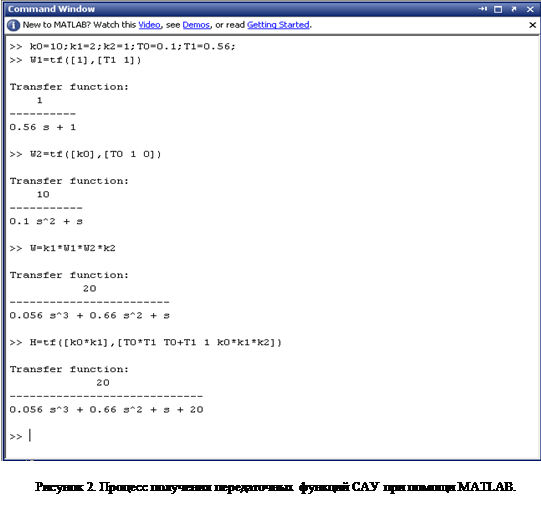
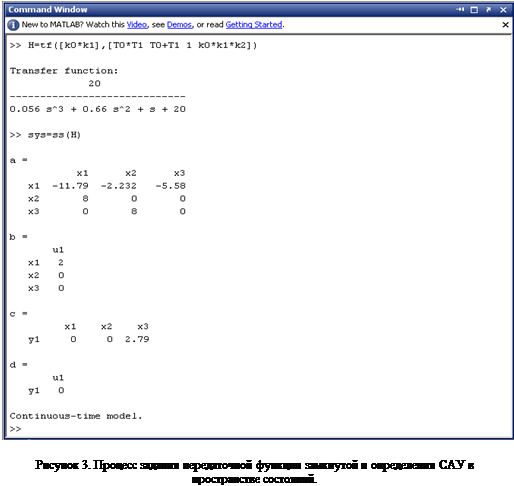
Передаточные функции звеньев САУ, представленной на рисунке (1), а также разомкнутой и замкнутой систем запишем в общем виде:

На рисунке 2 представлен фрагмент командного окна MATLAB, на котором изображен процесс определения параметров САУ, а на рисунке 3 – представление ее в виде модели в пространстве состояний.
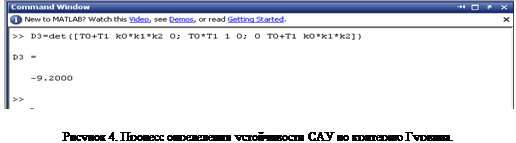
2. Проверка устойчивости системы по критерию Гурвица
На рисунке 4 представлен фрагмент командного окна MATLAB, на котором изображен процесс определения устойчивости системы согласно критерию Гурвица. Очевидно, что исследуемая САУ с заданными параметрами не является устойчивой, поскольку главный определитель системы отрицательный.
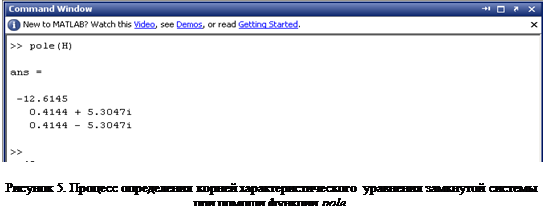
3. Определение устойчивости системы по корням характеристического уравнения
На рисунке 5 представлен фрагмент командного окна MATLAB, на котором изображен процесс определения корней характеристического уравнения замкнутой системы. Некоторые корни характеристического уравнения имеют положительные вещественные части, что характеризует систему как неустойчивую.
4. Определение назначения функций ltiview
и margin
. Получение с их помощью информации о переходной характеристике и запасе устойчивости системы
Функция ltiview
запускает так называемый LTIViewer – графический интерфейс пользователя, который упрощает анализ линейных времязависимых систем. Аргументом функции может быть специальная переменная, которая может содержать передаточную функцию системы, либо же описание в любом другом виде, например в пространстве состояний. При помощи LTIViewer можно генерировать временные или частотные графические отклики для изучения ключевых параметров этих откликов, таких как время нарастания сигнала, время регулирования, максимальная амплитуда максимальное перерегулирование и др.
На рисунке 6 представлен фрагмент командного окна MATLAB, на котором изображен процесс запуска интерфейса LTIViewer, а на рисунке 7 – график переходной характеристики системы, по которому однозначно можно судить о неустойчивости последней.

При помощи функции margin
можно оценить запас устойчивости системы. Функция выводит диаграмму Боде, на которой отмечает запасы устойчивости по амплитуде и фазе. На рисунке 8 представлен фрагмент командного окна MATLAB, на котором изображен процесс выполнения функции margin
, а на рисунке 9 изображена диаграмма Боде для САУ с заданными параметрами с отметками запасов устойчивости по амплитуде и фазе. Как видим, запас по амплитуде равен inf
(Gm = inf), а по фазе –43,9º (Pm = -43,9 deg), что свидетельствует о неустойчивости системы.
6. Проверка системы на устойчивость по критерию Михайлова
Для определения устойчивости по Михайлову проведем следующие манипуляции. Характеристический полином замкнутой системы имеет вид:
 . .
Вы полним замену переменных 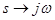 и получим частотозависимую функцию следующего вида: и получим частотозависимую функцию следующего вида:
 . .


Вещественная часть этой функции имеет вид:  , а мнимая: , а мнимая:  . .
Построим годограф Михайлова при помощи MATLAB, что изображено на рисунке 10. График годографа изображен на рисунке 11.


Как видно из рисунка 11, САУ с заданными параметрами неустойчива, поскольку вектор, начало которого лиежит в точке (0, 0), а конец – на кривой Михайлова, вращаясь против часовой стрелки НЕ проходит последовательно количество квадрантов, равное порядку системы – 3.
7. Проверка системы на устойчивость согласно критерию Найквиста
Построение амплитудно-фазовой характеристики (АФЧХ) разомкнутой системы выполняется в командном окне MATLAB при помощи функцииnyquist
:
>> nyquist(W)
где W – переменная, несущая информацию о передаточной функции разомкнутой системы.
На рисунке 12 построена АФЧЧ разомкнутой системы. Поскольку АФЧХ разомкнутой системы охватывает точку с координатами (-1, j0), то, согласно критерию Найквиста САУ с заданными параметрами является неустойчивой.

Выводы
В работе был проведен анализ устойчивости замкнутой автоматической системы на основании различных критериев при помощи ПО MATLAB.
Эффективность применения ЭВМ и ПО MATLAB в исследовании САУ высокого порядка на устойчивость очевидна, как при применения алгебраических критериев устойчивости, так и графических, поскольку пакет ControlSystem обладает широким набором функций для расчета и отображения характеристик сколь угодно сложной САУ, что было показано в работе.
Реализовать и исследовать модель регулирования "жесткого" спутника Земли.
Программа работы
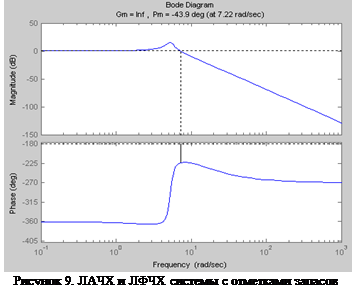
1. Исследовать переходную характеристику объекта регулирования – "жесткого" спутника Земли (ЖСЗ) в среде структурного моделирования Simulink с моментом инерции объекта J
= 10
.
2. Охватить динамическую модель "жесткого" спутника обратной связью по положению и оценить устойчивость САУ.
3. Охватить динамическую модель "жесткого" спутника обратной связью по скорости и положению. Системе дана команда изменить угловое положение на 30º. Определить это положение по окончанию переходного процесса. Определить коэффициенты регулятора при следующих коэффициентах демпфирования САР: ξ=0.707, ξ=1.
4. Оценить влияние на переходную характеристику изменения коэффициента обратной связи по скорости.
5. Оценить коэффициенты регулятора, если переходный процесс должен заканчиваться за 0,3 с, при g = 0.
6. Угловая скорость спутника измеряется с помощью гироскопического датчика. Предположим, что датчик вышел из строя (Подобные ситуации действительно имели место). Какой регулятор может обеспечить процесс регулирования САР?
7. Рассмотреть систему с чистым запаздыванием. Оценить динамические свойства системы при различных временах задержки: τ = 0.1 с, τ = 0,4 с, τ = 4 с.
8. Пронаблюдать фазовую траекторию САР.
1. Реализация модели "жесткого" спутника Земли в
Simulink
На рисунке 1 представлена структура модели "жесткого" спутника Земли для среды Simulink.

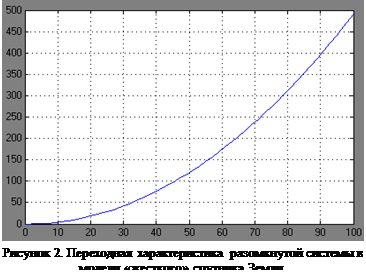
На рисунке 2 изображена переходная характеристика системы, из которой видно, что она не устойчива.
2. Охват модели ЖСЗ обратной связью по положению
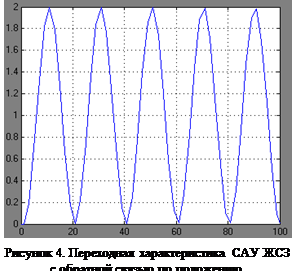
Структура модели ЖСЗ с единичной обратной связью по положению представлена на рисунке 3, ее переходная характеристика – на рисунке 4, вид которой соответствует консервативному звену. Такая САУ находится на границе устойчивости и неспособна привести объект в конечное положение.
3. Охват модели ЖСЗ обратной связью по скорости и по положению

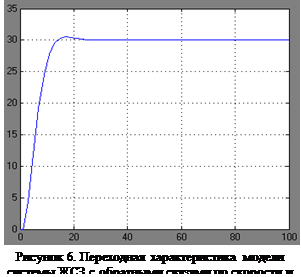
Структура модели ЖСЗ с обратной связью по скорости с фиксированным коэффициентом передачи и единичной обратной связью по положению изображена на рисунке 5. На рисунке 6. представлен график переходной характеристики системы при задающем ступенчатом воздействии в 30º.
Из переходной характеристики видно, что система, охваченная двумя обратными связями, приобретает устойчивость с приемлемыми параметрами регулирования: перерегулирование составляет примерно 3,3 %, а время регулирования – около 17 с. Установившееся значение выходного угла соответствует заданному.
Общее выражение передаточной функции структуры на рисунке 5 имеет вид:
 . .
Определим величину коэффициента обратной связи по скорости при заданных коэффициентах демпфирования  . Очевидно что: . Очевидно что:
 . .
Тогда:

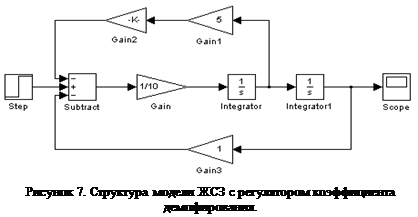
Для возможности изменения коэффициента демпфирования в линию местной обратной связи вводится регулятор с изменяемым коэффициентом передачи K
и тогда структура модели приобретает вид, изображенный на рисунке 7.
4. Оценка влияния изменения коэффициента обратной связи по скорости на переходную характеристику системы
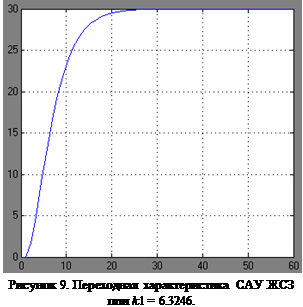
Построим переходные характеристики для двух значений k
1
, определенных в п.п. 3. Графики этих кривых представлены на рисунках 8 и 9.
Как видно из рисунков 8 и 9 увеличение коэффициента передачи сигнала обратной связи по скорости приводит к уменьшению перерегулирования и увеличению времени регулирования системы.
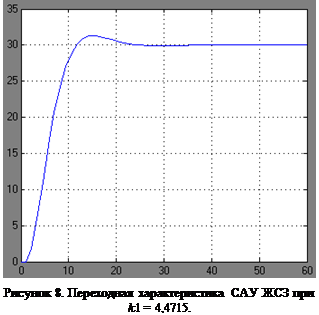
5. Определение коэффициентов обратных связей САУ при известном времени окончания переходного процесса
Если задано время переходного процесса в системе: 0,3 с, при отсутствии задающего воздействия, то можно определить коэффициенты обратных связей САУ из соображений:

где k
1, k
2 – коэффициенты обратных связей по скорости и положению соответственно; t
р
– время регулирования; λ1
– один из корней характеристического уравнения системы.
Если принять второй корень характеристического уравнения равным: 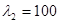 , то получим: , то получим:


На рисунке 10 приведена структура САУ, удовлетворяющей заданным условиям, а на рисунке 11 – ее переходная характеристика. В модели САР множитель J
выделен в отдельный блок.
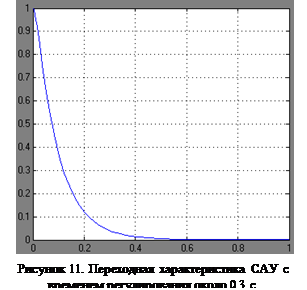
6. Система с чистым запаздыванием. Оценка динамических свойств системы с различными временами задержки

Структура модели ЖСЗ со звеном запаздывания изображена на рисунке 12.
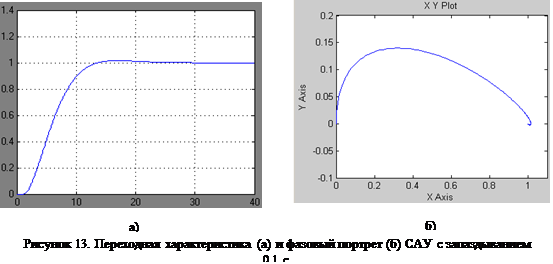
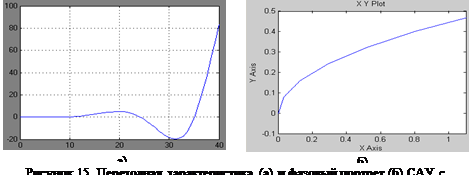
Ни рисунках 13, 14 и 15 приведены переходные характеристика и фазовые траектории САУ с запаздыванием  , ,  и и  соответственно. соответственно.
Очевидно, что запас устойчивости уменьшается и ухудшаются показатели регулирования САУ со звеном запаздывания, вплоть до полной неустойчивости системы при увеличении времени запаздывания (рис. 15).
Исследование модели ЖСЗ показало, что САУ ЖСЗ является неустойчивой в разомкнутом состоянии. В ведение единичной обратной связи по положению переводит систему на колебательную границу устойчивости и конечное угловое положение объекта управления не определено. Система становится устойчивой и управляемой при введении местной обратной связи по угловой скорости. Такая система обладает приемлемыми показателями качества регулирования и способна отрабатывать задания на угловые перемещения. Введение дополнительного регулятора в канал местной обратной связи позволяет управлять демпфированием системы, что было показано. САУ с чистым запаздыванием может быть как устойчивой с приемлемыми показателями качества регулирования, так и неустойчивой. Увеличение времени запаздывания ведет к усилению колебательных свойств системы и переходу ее в неустойчивое состояние.

|