| БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
кафедра ЭТТ
РЕФЕРАТ на тему:
«
Теория идеальных оптических систем (параксиальная или гауссова оптика)
»
МИНСК, 2008
В параксиальной области (бесконечно близко к оптической оси), любая реальная система ведет себя как идеальная:
Каждой точке пространства предметов можно поставить в соответствие сопряженную ей точку в пространстве изображений.
Каждая прямая линия имеет сопряженную ей прямую линию в пространстве изображений.
Каждая плоскость пространства предметов имеет сопряженную ей плоскость в пространстве изображений. Из этих положений следует, что:
Меридиональная плоскость имеет сопряженную ей меридиональную плоскость в пространстве изображений.
Плоскость в пространстве предметов, перпендикулярная оптической оси, имеет сопряженную ей плоскость, перпендикулярную оптической оси в пространстве изображений.
Линейное (поперечное) увеличение
Линейное увеличение оптической системы
– это отношение линейного размера изображения в направлении, перпендикулярном оптической оси, к соответствующему размеру предмета в направлении перпендикулярном оптической оси (рис.1):
 . (1)
Рисунок 1 – Сопряженные линейные величины
Если β>0
, то отрезки y
и y΄
направлены в одну сторону, если β<1
, то отрезки y
и y΄
направлены в разные стороны, то есть происходит оборачивание изображения.
Если │β│>1
, то величина изображения больше величины предмета, если│β│<1
, то величина изображения меньше величины предмета.
Для идеальной оптической системы линейное увеличение для любой величины предмета и изображения в одних и тех же плоскостях одно и то же. Угловое увеличение
Угловое увеличение оптической системы
– это отношение тангенса угла между лучом и оптической осью в пространстве изображений к тангенсу угла между сопряженным с ним лучом в пространстве предметов и осью (рис.2):
 . (2)
Рисунок 2 – Сопряженные угловые величины
В параксиальной области углы малы, и следовательно, угловое увеличение – это отношение любых из следующих угловых величин:
 . (3)
Продольное увеличение
Продольное увеличение оптической системы
– это отношение бесконечно малого отрезка, взятого вдоль оптической оси в пространстве изображений, к сопряженному с ним отрезку в пространстве предметов (рис.3):
 . (4)
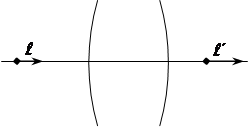
Рисунок 3 – Сопряженные продольные отрезки
Рассмотрим плоскости в пространстве предметов и сопряженные им плоскости в пространстве изображений. Найдем пару плоскостей, в которых линейное увеличение равно единице. В общем случае такая пара плоскостей существует, причем только одна (исключением являются афокальные или телескопические системы, для которых такие плоскости могут не существовать или их может быть бесконечное множество).
Главными плоскостями системы
называется пара сопряженных плоскостей, в которых линейное увеличение равно единице (β=1).
Главные точки
H
и H΄
– это точки пересечения главных плоскостей с оптической осью.
Рассмотрим случай, когда линейное увеличение равно нулю, или бесконечности. Отодвинем плоскость предметов бесконечно далеко от оптической системы. Сопряженная ей плоскость называется задней фокальной плоскостью
, а точка пересечения этой плоскости с оптической осью – задний фокус
F΄
(рис.4).
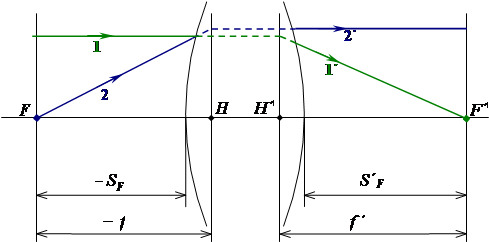
Рисунок 4 – Кардинальные точки и отрезки
Расстояние от задней главной точки до заднего фокуса называется задним фокусным расстоянием
f΄
.
Расстояние от последней поверхности до заднего фокуса называется задним фокальным отрезком
 .
Передний фокус
F
– это точка на оптической оси в пространстве предметов, сопряженная с бесконечно удаленной точкой, расположенной на оптической оси в пространстве изображений.
Если лучи выходят из переднего фокуса, то они идут в пространстве изображений параллельно.
Переднее фокусное расстояние
f
– это расстояние от передней главной точки до переднего фокуса.
Передний фокальный отрезок
 – это расстояние от первой поверхности до переднего фокуса.
Если  , то система называется собирающей
или положительной.
Если  , то система рассеивающая
или отрицательная.
Переднее и заднее фокусные расстояния не являются абсолютно независимыми, они связаны между собой соотношением:
 . (5)
Выражение (5) можно переписать в виде:
 , (6)
где  – приведенное
или эквивалентное фокусное расстояние
.
В том случае, если оптическая система находится в однородной среде (например, в воздухе)  , следовательно, переднее и заднее фокусные расстояния равны по абсолютной величине  .
Оптическая сила
оптической системы:
 . (7)
Чем больше оптическая сила, тем сильнее оптическая система изменяет ход лучей. Если  то .
Найдем изображение A΄
точки A
.
Для этого необходимо построить хотя бы два вспомогательных луча, на пересечении которых и будет находиться точка A΄
(рис.5). Вспомогательный луч 1
можно провести через точку A
параллельно оптической оси. Тогда в пространстве изображений луч 1
΄
пройдет через задний фокус оптической системы. Вспомогательный луч 2
можно провести через точку А
и передний фокус оптической системы. Тогда в пространстве изображений луч 2
΄
пойдет параллельно оптической оси. На пересечении лучей 1
΄
и 2
΄
будет находиться изображение точки A
. Теперь в точке A΄
пересекаются все лучи (1-2-3
), выходящие из точки A
.
Рисунок 5 – Построение изображения точки
Построим теперь ход луча r
(рис.6).
1 способ
. Можно построить вспомогательный луч, параллельный данному и проходящий через передний фокус (луч 1
). В пространстве изображений луч 1
΄
будет идти параллельно оптической оси. Так как лучи r
и 1
параллельны в плоскости предметов, то в пространстве изображений они должны пересекаться в задней фокальной плоскости. Следовательно, луч r΄
пройдет через точку пересечения луча 1
΄
и задней фокальной плоскости.
2 способ
. Можно построить вспомогательный луч, идущий параллельно оптической оси и проходящий через точку пересечения луча r
и передней фокальной плоскости (луч 2
). Соответствующий ему луч в пространстве изображений (луч 2΄
) будет проходить через задний фокус. Так как лучи r
и 2
пересекаются в передней фокальной плоскости, в пространстве изображений они должны быть параллельными. Следовательно, луч r΄
пойдет параллельно лучу 2
΄
.
Рисунок 6 – Построение хода луча
Основные соотношения параксиальной оптики
Основные соотношения параксиальной оптики связывают между собой фокусные расстояния, положение и размеры предмета и изображения, угловое, линейное и продольное увеличения.
Рисунок 7 – Схема для вывода основных соотношений параксиальной оптики
Для вывода зависимости между положением и размером предмета и изображения воспользуемся рис.7.  подобен  , следовательно:
 , отсюда  .
Тогда, в соответствии с выражением (1), линейное увеличение можно выразить следующим образом:
 . (8)
Аналогично, из подобия треугольников  и  можно получить выражение:
 . (9)
Таким образом, увеличение можно выразить как через передние, так и через и задние отрезки. Отсюда можно получить формулу Ньютона
:
 . (10)
Если оптическая система находится в однородной среде ( ), то  , и формула Ньютона получает вид:
 . (11)
Выразим z
и z΄
через фокусные расстояния и передний (-a) и задний (a΄) отрезки:
 .
Тогда выражение (11) можно записать в виде:
 .
После преобразований получим выражение, связывающее фокусные расстояния и передний и задний отрезки (формула отрезков
или формула Гаусса
):
 . (12)
Теперь рассмотрим угловое увеличение, опять воспользовавшись рис.7. Из  , видно, что:
 , отсюда  .
Аналогично можно вывести выражение:
 .
Теперь можно выразить угловое увеличение через передний и задний отрезки:
 (13)
Выразим z΄ из формулы Ньютона (5.14), тогда после преобразований получим выражение для вычисления углового увеличения:
 (14)
Из выражения (14) следует, что если выбрать плоскости предмета и изображения таким образом, что  и  , то в точках пересечения этих плоскостей с осью угловое увеличение равно единице. Такие точки называются узловыми точками
.
Чтобы найти узловые точки N и N΄, от переднего фокуса откладывается заднее фокусное расстояние, а от заднего фокуса откладывается переднее фокусное расстояние (рис.8). Отрезки NN΄ и HH΄ равны. Если  ( ), то узловые точки совпадают с главными.
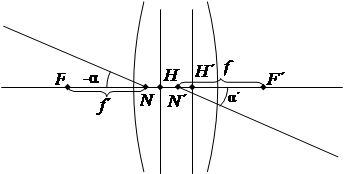
Рисунок 8 – Узловые точки
Следствием выражений (5.13) и (5.18) является следующее соотношение:
 (15)
Рассмотрим различные положения предмета и изображения (различные z и z΄):
-  . Тогда  , линейное увеличение  , следовательно, предмет и изображение – это главные плоскости. Угловое увеличение  .
- . Тогда , угловое увеличение W=1, следовательно, предмет и изображение – это узловые точки. Линейное увеличение  .
-  . Тогда  , линейное увеличение  , угловое увеличение  , следовательно, предмет находится на двойном фокусном расстоянии, то есть расстояние между предметом и изображением минимально.
-  . Тогда  , линейное увеличение  , угловое увеличение  , следовательно, предмет находится в переднем фокусе, а изображение – в бесконечности.
-  . Тогда  , линейное увеличение  , угловое увеличение  , следовательно, предмет находится на бесконечности, а изображение – в заднем фокусе.
Рисунок 9 – Связь продольного увеличения с поперечным и угловым
Рассмотрим рис.9. Длину отрезков l
и l΄
можно выразить следующим образом:
 .
По определению продольного увеличения:
 .
После преобразований, получим:
 (16)
где β и β1
– поперечные (линейные) увеличения в точках A΄
и A
1
΄
.
Или, :
 . (17)
Теперь рассмотрим продольное увеличение для бесконечно малых отрезков ( ) (по определению это и есть продольное увеличение). В этом случае линейное увеличение в точках A΄
и A΄
1
будет одинаковым, следовательно:
 . (18)
Из выражения (16) можно получить:
 (19)
Если оптическая система находится в однородной среде ( ), то:
 . (20)
То есть продольное увеличение равно квадрату линейного увеличения, а угловое обратно пропорционально ему.
Диоптрийное исчисление
– это измерение продольных отрезков в обратных единицах (диоптриях):
где  – приведенная длина.
Одна диоптрия соответствует приведенному отрезку в 1м. Если отрезок измеряется в мм, то обратный отрезок измеряется в килодиоптриях.
Используя формулу отрезков (5.16) и выражение (5.9) можно получить важное соотношение для приведенных отрезков в пространстве предметов и изображений и оптической силы, измеряемых в диоптриях:
или
 (21)
где D
и D΄
– приведенные передний и задний отрезки в диоптриях. То есть оптическая система увеличивает приведенный отрезок в пространстве изображений (в дптр) на величину оптической силы.
Инвариант Лагранжа-Гельмгольца связывает линейный размер предмета и угловой размер пучка лучей (рис.10). Эта величина инвариантна, то есть неизменна в любом пространстве.
Рисунок 10 – Величины, которые связывает инвариант Лагранжа-Гельмгольца
Для вывода этого инварианта воспользуемся выражением (18), связывающим угловое и линейное увеличения. Тогда воспользовавшись выражениями (5.5) и (5.7), определяющими линейное и угловое увеличения, получим следующее соотношение:
 . (22)
Выражение (22) можно преобразовать, и тогда получим инвариант Лагранжа-Гельмгольца:
 . (23)
Инвариант Лагранжа-Гельмгольца характеризует информационную емкость оптической системы, то есть величину пространства, которое может быть отображено оптической системой. Этот инвариант математически выражает закон сохранения информации в геометрической оптике.
ЛИТЕРАТУРА
Бегунов Б.Н., Заказнов Н.П. и др. Теория оптических систем. – М.: Машиностроение, 2004 2004
Заказнов Н.П. Прикладная оптика. – М.: Машиностроение, 2002 2002
Дубовик А.С. Прикладная оптика. – М.: Недра, 2002 2002
Нагибина И.М. и др. Прикладная физическая оптика. Учебное пособие.- М.: Высшая школа, 2005 2005
|
