Курсовая работа: Составление теоретической конструкции балки

Курсовая работа

Тема: Составление теоретической конструкции балки

Содержание

1 Теоретические основы создания балки

2 Создание балки из конкретного металла с заданными характеристиками

3 Другие элементы

4 Расчет нагрузки на элементы

5 Определение размеров рам

1 Теоретические основы создания балки

1.1 Построение эпюр Qy и Mx. Опорные реакции

Σ Yi = 0, RAy –qa+ qa– F =0,

Ray = F= 3qa = 50,4кН,

Σ ma= 0, – МA+0,5qa2 – 1,5a∙qa – 2qa2 + 3qa∙3a = 0,

– МA+0,5qa2 – 1,5qa2 – 2qa2 +9qa2 = 0,

– MA = – 6qa2.

Эпюра Qy. Она строится по формуле Q=Q0 ±qz. В данном случае стоит взять знак «минус» для участка балки АВ, (так как погонная нагрузка направлена вниз), и знак «плюс» для участка балки ВС (погонная нагрузка направлена вверх). Поперечная сила постоянна на участке СD (т.к. q=0) и изображается прямой, параллельной оси Оz, на участках АВ и ВС – наклонной прямой (q=const). Вычисляем значения Qy в характерных точках

QA = RAy=3qa, кН,

QAB = QA – qa =3qa – qa=2qa , кН,

QВС = QAB +qa = 2qa+qa = 3qa, кН,

QСD = QВС = 3qa , кН и строим ее эпюру.

Эпюра Мх. Она строится по формуле Мх = М0+Q0z–0,5qz2. Изгибающий момент изменяется по квадратичному закону на участках АВ и ВС (т.к. q=const), и по линейному закону на участке СD (q=0). По значениям момента в характерных точках

MA = – 6qa2, кH∙м,

MAB = MA + Ray∙a = – 6qa2 + 3qa2 = – 3qa2, кH∙м,

MBC = MAB +2qa∙ a = – 3qa2 + 2qa2 = – qa2, кH∙м,

MCD = MBC – 2qa2 = – qa2– 2qa2 = – 3qa2, кH∙м,

MF = – 3qa2+ 3qa2=0

строим эпюру Мх. Расчетный изгибающий момент равен

Mрас = │ MA │= 6 qa2 = 120,96 кH∙м.

1.2 Подбор сечений

Из условия прочности по нормальным напряжениям σмах=Мрас/Wx≤ [σ] определяем требуемый момент сопротивления поперечного сечения

Wx ≥ Mрас /[σ] = 120,96 ∙103/160∙106 = 756 см3,

по которому подбираем конкретные сечения.

Круг: Wx = πd3/32,

= =19,75 см.

Принимаем по ГОСТ 6636-86 нормализованное значение d0 = 200 мм, тогда А1 = π d02/4 = π ∙ 202/4 =314 см2.

Прямоугольник (h/b = 2) Wx=b∙(2b)2/6=2b3/3,

b ≥ 3√3 Wx /2 = = 10,43 см.

Ближайшее меньшее значение равно b0=100мм. При этом балка будет работать с перенапряжением, равным

δσ = [(b3-b03)/ b03] ∙100% =[10,433 – 103/ 103] ∙ 100% = 13,46%,

что недопустимо. Поэтому принимаем ближайший больший размер b0=105 мм, для которого А2=2b02= 2 ∙ 10,52 = 220,5 см2.

Двутавр. По ГОСТ 8239-89 выбираем двутавр №36, для которого Wх=743,0 см3, А3 = 61,9 см2.

Два швеллера. По ГОСТ 8240-89 выбираем два швеллера № 30, для которых Wх = 2∙387 = 774 см3, А4 = 2 ∙ 40,5 = 81см2.

Неравнобокие уголки. Они находятся подбором, так как в сортаменте не даны значения момента сопротивления. Используя формулу Wx=2Ix/(b – y0), сделаем несколько попыток, выбираем два уголка 250х160х20, для которых Wх = 2∙4987/(25 – 8,31) = 597,6 см3, А5 = 2∙78,5 = 157,0 см2.

1.3 Оценка экономичности подобранных сечений

Масса балки определяется как произведение плотности материала на ее объем m=ρAl, т.е. расход материала при прочих равных условиях зависит только от площади поперечного сечения А. Сравнивая массы балок:

m1 : m2 : m3 : m4 : m5 = A1 : A2 : A3 : A4 : A5 = 1 : 0,7 : 0,2 : 0,26 : 0,5,

заключаем, что самым неэкономичным является круглое сечение. При замене круга другими формами (прямоугольник, двутавр, два швеллера, два уголка) достигается экономия, равная соответственно 30%, 80%, 74% и 50%.

Исследование напряжений в опорном сечении для балки двутаврового профиля №36, параметры которой по ГОСТ 8239-89 равны:

h = 36 см, b = 14,5 см, d = 0,75 см, t = 1,23 см,

Ix = 13380 см4, Sx = 423 см3.

Внутренние силовые факторы в опорном сечении А:

QA= 3qa = 3∙14∙1,2 = 50,4 кН;

MA= – 6qa2 = – 6∙14∙1,22 = –120,96 кН∙м.

Эпюра σ. Нормальные напряжения в поперечном сечении изменяются по линейному закону σz=(Mx/Ix)y. Вычисляем напряжения в крайних точках

Σmax= σmin = Mx/ Wx = 120,96 ∙103/756∙10-6 = 160 МПа

и строим эпюру σ

Эпюра τ. Она строится по формуле Журавского τ=.

Находим значения τ в 4 характерных точках по высоте сечения и строим эпюру касательных напряжений.

Определение главных напряжений в точке К (ук=0,4h):

– напряжения в поперечном сечении

σк = (МА/IA) ∙YK= (–120,96∙103/13380∙10-8) ∙0,4∙36∙102 = – 130МПа,

τK = = 50,4∙103∙ 338∙10-6 /(0,75∙10-2∙13380 ∙10-8) = 17МПа;

– величины главных напряжений

σ 1,3 =0,5(σк±)=0,5(–130±),

σ1 = 2,2 МПа; σ3 = – 132,2 МПа – ориентация главных площадок

tgα1 = (σ1 – σк)/τk= (2,2 – ( –130))/17 = 7,78;

α1 = 82040′.

Экстремальные касательные напряжения равны по величине

τmax, min= ±0,5(σ1- σ3)= ±0,5(2,2 + 132,2) = ± 67,2 МПа

и действуют на площадках, равнонаклоненным к осям 1 и 3. Графическое определение главных напряжений и положения главных площадок.

2 Создание балки из конкретного металла с заданными характеристиками

2.1 Построение эпюр поперечной силы и изгибающего момента. Опорные реакции

Σmв=0, – RA·3a + 1,5qa2 + q·3a·2,5a – 3·qa·a = 0, RA = 2qa;

ΣYi=0, RA – q·3a + RB – 3qa =0, RB = 4qa.

Эпюра Qy.

Поперечная сила постоянна на участке ЕВ и ВС; изменяется по линейному закону на участке DA и AE и принимает следующие значения:

QD = 0, QAD = QD – qa = – qa,

QA = QAD + RA = – qa + 2qa = qa, QAE = QA – q·2a = qa – 2qa = – qa,

QEB = QAE = – qa, QB = QEB+ RB = – qa + 4qa = 3qa,

QB = QC = 3qa.

Эпюра Мх.

Изгибающий момент изменяется по линейному закону на участке EB и BC, по квадратичному закону на участках DA и AE, принимая экстремальные значения в сечении z = 4а. По значениям момента в характерных точках

MD = 0, MA = – qa·0,5a = – 0,5qa2 ,

M (2a) = – 2qa·a + RA·a = – 2qa2 + 2qa2 = 0,

ME = – 3qa·1,5a + RA·2a = – 4,5qa2 + 4qa2 = – 0,5qa2 ,

MEB = ME + 1,5qa2 = – 0,5qa2 + 1,5qa2 = qa2 ,

Mmax = MB = – 3qa·2,5a + RA·3a – 1,5qa2 = – 3 qa2,

MC = 0.

строим эпюру Мх, из которой находим расчетный изгибающий момент

Мрас= 3qa2 = 60,48 кН∙м

2.2 Определение перемещений

2.2.1 Метод начальных параметров

Из граничных условий имеем: vA = 0, vB = 0. Отсюда находим v0 , θ0:

vA= v(a) = v0 + θ 0∙а + ,

vB=v(4a)=v0+ θ0∙4а +;

θ 0 = – ;

v0 = – = 0; v0 = .

А теперь находим искомые перемещения:

- сечение z = а

θ (а) = θ0 + ;

V(а) = 0;

- сечение z = 2а

θ(2а) = θ0 + ;

v(2а) = v0+ θ0∙2a+;

- сечение z = 3а

θ(3а) = θ0 + = ;

v(3a) = v0 + θ0∙3a + ;

- сечение z = 4а

v(4a) = 0;

θ(4а)=θ0+ =;

- сечение z = 5а

θ(5а)=θ0+ = ;

V(5a)=V0+θ0∙5a+ .

Результаты вычислений сведем в таблице и построим упругую линию балки пунктиром

Для расчета балки на жесткость необходимо знать максимальный прогиб, который имеет место в сечении, где угол поворота равен нулю. Он имеет место в сечении z = 3а, отсюда vmax= vВ = 8qa4/(9 EIx)

2.2.2.Энергетический метод

Строим эпюры моментов от заданной нагрузки и от единичных воздействий, приложенных к балке в направлении искомых перемещений. Определяем моменты посередине участков.

МсрDА = (МС + МА)/2 + qа2/8 = (0 + 1/2) qа2 + qа2/8 = 3/8 qа2,

МсрАM = (МA + МM)/2 + qа2/8 = (0 + 1/2) qа2 + qа2/8 = 3/8 qа2,

МсрME = (МM + МE)/2 + qа2/8 = (0 + 1/2) qа2 + qа2/8 = 3/8 qа2,

МсрEB =(МE + МB)/2 = (1 + 3) qа2/2 =1/2 qа2,

МсрBС =(МB + МC)/2 = (3 + 0) qа2/2 = 3/2qа2.

Перемножая соответствующие эпюры, находим искомые перемещения, увеличенные для удобства вычислений в EI раз:

EIxvB=;

ЕIxθA=;

ЕIxθB=.

2.2.2 Расчет на ЭВМ методом конечных элементов

Исходные данные вво- дятся в безразмерной форме:

ζ = z /a (0 ≤ ζ ≤ 10), , .

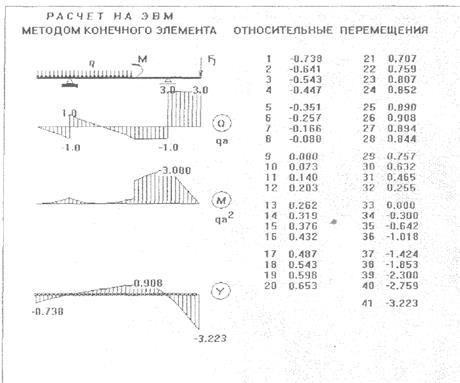
Из рисунка следует, что наибольший прогиб имеет место в сечении 3a, где возникает наибольший изгибающий момент, и равен

.

2.2.4 Подбор сечения неравнобоких уголков по условиям прочности и жесткости

Из условия прочности имеем σmax = Mmax/Wx ≤ [σ].

Отсюда, учитывая что Mmax = – 3 qa2,

[σ]=,

σвр=, Fте находим из диаграммы растяжения

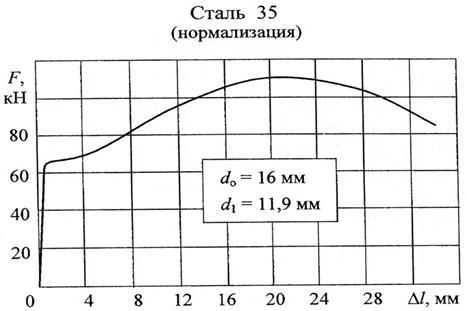
σвр = = 318 МПа,

[n] = 1,5 если > 5%, [n] = 2,4 если < 5%,

= =0,7%,

[σ] = 318/2,4=132,5 МПа, отсюда Wx ≥ Mmax/ [σ]=60,48∙103/132,5∙106 = 456 см3.

Условиям прочности удовлетворяет Wx ≥ 456 см3

Согласно условиям жесткости

≤ [f],

откуда l/[f] = 900, [f] = l/900 =2,5/900 = 2,8 мм

Ix ≥== 4608 см4;

Учитывая условия прочности и жесткости по ГОСТу 8510-86 выбираем неравнобокие уголки №27 с следующими параметрами:

B=250мм, b=160 мм, d=18мм, A=157 см2, Ix=4987см4, Wx=597,6см3.

3 Другие элементы

3.1 Раскрытие статической неопределимости

Данная система дважды статически неопределима (две дополнительные связи), поэтому канонические уравнения имеют вид:

Коэффициенты при неизвестных, увеличенные в EI раз:

Проверка:

Свободные члены, увеличенные в EI раз:

;

Проверка: ;

Канонические уравнения имеют вид:

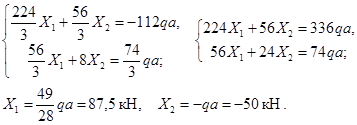
3.2 Определение опорных реакций

3.3 Построение эпюр внутренних силовых факторов

Эпюра Q. Эпюра строится по формуле . Вычисляем значения Q в характерных точках:

и строим эпюру Q.

Эпюра M. Эпюра строится согласно выражению

.

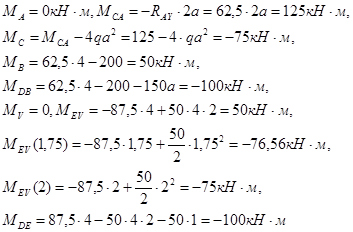
Эпюра N. Деформацию сжатия испытывают стержни BC и CD. Продольная сила в пределах каждого участка постоянна и принимает следующие значения:

3.4 Проверка решения

3.4.1Статическая проверка

Узел B

Узел C

3.4.2 Кинематическая проверка. Проверка состоит в выполнении условия

.

4 Расчет нагрузки на элементы

4.1 Определение геометрических характеристик сечения

а)Координаты центра тяжести.

uc=0, vc==384t3/48t2=8t.

б) Моменты инерции относительно главных центральных осей x, y.

Предварительно вычисляем осевые моменты инерции отдельных частей относительно собственных центральных осей ξiηi

I= 8t·(4t)3/12 = 42,67t4,

I= 2·t·(8t)3/12 = 85,33t4,

I= 4t·(8t)3/12 = 170,67t4,

I= 2·8t·t3/12 = 1,33t4.

Остальные вычисления представим в табличной форме.

в) Главные радиусы инерции

ix2 = Ix/A = 512t4/(48t2) = 10,67t2;

iy2 = Iy/A = 208t4/(48t2) = 4,33t2.

Построение ядра сечения. Для фигуры с прямолинейными сторонами ядро сечения представляет собой выпуклый многоугольник, координаты вершин которого определяются формулами:

xяi= – iy2/ai , yяi= – ix2/bi .

Здесь ai и bi – отрезки, отсекаемые нейтральной линией на осях координат, при ее обкатывании вокруг контура сечения. Выполняя необходимые вычисления в табличной форме, получим ядро сечения.

4.2 Определение размеров сечения

Отрезки, отсекаемые нейтральной линией на осях координат

ао= – iy2/xf = –4,33t 2/(4t) = –1,083t;

bо= – ix2/yf = –10,67t 2/0 = ∞.

Проводим нейтральную линию nn и устанавливаем опасные точки. Это будут точки 1 и 6 как наиболее удаленные от нейтральной оси.

Из условия прочности на растяжение

σmax = ,

σmax = ,

откуда мм.

Из условия прочности на сжатие

σmin = ,

σmin = ,

откуда

Следовательно, t = max = tp = 27,3 мм. Принимаем по ГОСТ 6636 =28 мм. Для ближайшего меньшего размера (=26 мм) будет перенапряжение 15,7%, что недопустимо.

4.3 Построение эпюры нормальных напряжений. Исходя из принятых размеров сечения, находим напряжения в опасных точках

МПа;

МПа

и строим эпюру σ.

5 Пространственные рамы

5.1 Устанавливаем опасное сечение для каждого из стержней

AB – сечение А, где Mx = 3qa2, My = qa2, Mz = 2qa2;

Qx = 0, Qy = 2qa, NA = qa.

AB – сечение B, где Mx = qa2, My = qa2, Mz = 2qa2;

Qy =2qa, NA = qa.

BC – сечение B, где Mx = qa2, My = 2qa2, Mz = 0,5qa2;

Qy =qa, N = 2qa.

BC – сечение C, где Mx = 0, My = 2qa2, Mz = 0,5qa2;

Qy =qa, N = 2qa.

CD – сечение C, где Mx = 0,5qa2, My = 2qa2;

Qx = 2qa , Qy = qa.

CD – сечение D, где Mx = 0, My = 0;

Qx = 2qa , Qy = 0.

5.2 Подбор сечений стержней

Сечение А Стержень АВ

Он испытывает изгиб в двух плоскостях, кручение, сдвиг и сжатие.Так как Mx > My, то рациональным будет такое расположение сечения, при котором Wx > Wy, т.е. длинная сторона прямоугольника должна быть параллельна оси y. Для установления опасной точки необходимо вычислит эквивалентные напряжения в трех точках контура сечения. Из них опасной будет та точка, в которой σэкв является наибольшим. При подборе сечений будем пренебрегать в первом приближении продольными и поперечными силами.

Точка 1. В этой точке возникает линейное напряженное состояние, поэтому

.

Так как h/b=1,5, то h = 1,5b;

, .

Следовательно,

.

Точка 2. В этой точке возникает плоское напряженное состояние, поэтому

.

Так как , ,

Следовательно,

.

Точка 3. В этой точке возникает плоское напряженное состояние, поэтому сог-ласно III гипотезе прочности

.

Так как , ,

Следовательно, .

Так как , то опасной является точка 2.

Записываем условие прочности для точки 2

.

Отсюда мм.

Принимаем по ГОСТ 6636 bo =160 мм. Следовательно, стержень АВ должен иметь сечение 16x24 см.

Так как подбор сечения выполнен без учета продольной и поперечной сил, то необходимо проверить прочность стержня, принимая во внимание все внутренние силовые факторы, возникающие в опасном сечении. Рассмотрим опасную точку 2 и вычислим в ней нормальные, касательные и эквивалентные напряжения.

Нормальные напряжения:

- от изгиба

МПа;

- от продольной силы

МПа;

- суммарные

МПа.

Касательные напряжения:

- от кручения

МПа;

- от поперечной силы

МПа;

- суммарные

МПа.

Эквивалентное напряжение

МПа.

Без учета продольной и поперечной сил

МПа.

Как видим, расхождение между и не превышает 3%, т.е. лежит в пределах инженерного расчета. Поэтому на практике продольными и поперечными силами, как правило, пренебрегают.

Условие прочности стержня АВ при принятых размерах поперечного сечения выполняется, так как

МПа.

Сечение В Стержень ВС

Он испытывает изгиб в двух плоскостях, кручение, сдвиг и сжатие. Пренебрегая продольной и поперечной силами, условие прочности можно записать в виде ,

где - эквивалентный момент по III гипотезе прочности, равный

.

Следовательно, ,

откуда мм.

Принимаем по ГОСТ 6636 do=190мм.

Сечение С Стержень СD

Он испытывает изгиб в двух плоскостях, т.е. косой изгиб. Так как Mx < My, то сечение следует расположить длинной стороной вдоль оси x. В этом случае будет выполняться условие Wx<Wy, т.е.большему изгибающему моменту будет соответствовать больший момент сопротивления

Так как h/b=2, то h = 2b;

, .

Условие прочности

.

Отсюда мм.

Принимаем по ГОСТу 6636 do=110мм. Искомое сечение стержня будет 11x18 см.

6 Определение размеров рам

Дано:

Значения коэффициента продольного изгиба φ, увеличенные в 1000 раз, приведены в таблице:

6.1 Определение геометрических характеристик сечения

- площадь ;

- минимальный момент инерции

Imin = ;

- минимальный радиус инерции

.

Полученные характеристики можно записать в общем виде следующим образом:

,

где ; d = а – характерный размер сечения.

6.2 Подбор поперечного сечения

Искомый характерный размер сечения находится из трансцендентного уравнения

,

которое решается методом последовательных приближений.

Первое приближение. Примем , тогда

Гибкость стержня равна .

По таблице , используя формулу линейной интерполяции

,

находим .

Ввиду большой разницы между φ1 и делаем второе приближение, принимая

Имеем: .

Расхождение , то есть подбор закончен. Следовательно, характерный размер сечения должен быть не менее . Принимаем по ГОСТ 6636: .

6.3 Определение коэффициента запаса устойчивости

Гибкость стержня при принятых размерах сечения равна

.

Поскольку , то стержень обладает средней гибкостью и для определения критической силы следует воспользоваться эмпирической формулой

.

Коэффициент запаса устойчивости равен