Министерство образования и науки Украины
Донбасская Государственная Машиностроительная Академия
Кафедра АПП
Лабораторная работа
по дисциплине
"Теория автоматического управления"
Выполнил
Проверил
Краматорск
Тема: Исследование частотных свойств линейных динамических звеньев
Исследуем апериодическое звено I-го порядка. Передаточная функция звена:
 , где  с
Теоретический расчет
1) Определение частотных характеристик звена.
Определяем активную и реактивную составляющие:
 
Зависимость амплитуды от частоты имеет вид
Зависимость угла сдвига фаз от частоты имеет вид
Построим графики АЧХ (рис.1), ФЧХ (рис.2) и АФЧХ (рис.3) звена.
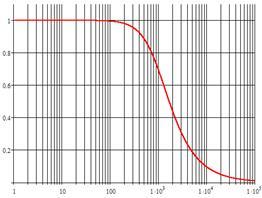
Рисунок 1 - амплитудно-частотная характеристика апериодического звена I-го порядка
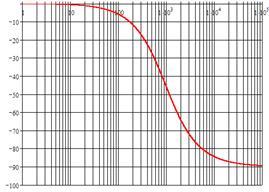
Рисунок 2 - фазо-частотная характеристика апериодического звена I-го порядка.
Рисунок 3 - амплитудно-фазовая характеристика апериодического звена I-го порядка.
2) Построим логарифмические частотные характеристики апериодического звена I-го порядка.
Определяем коэффициент усиления звена: K = 1
Кол-во чистых  на низких частотах наклон = 0
Определяем сопрягающие частоты:
По полученным результатам строим ЛАЧХ и ЛФЧХ звена (рис.4).
Рисунок 4 - логарифмические частотные характеристики апериодического звена I-го порядка
Практический расчет
Определим характеристики  и  экспериментальным путем.
Для этого используем измерительный стенд (рис.5).
На вход исследуемого звена подадим синусоидальный сигнал.
Модуль вектора  равен отношению амплитуд выходного и входного сигналов.
Фазовую характеристику получаем путем измерения фазового сдвига между входным и выходным сигналами.
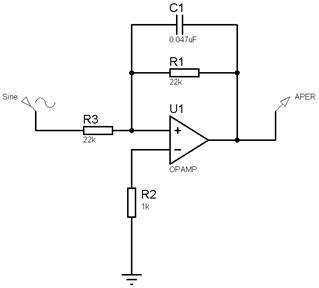
Рисунок 5 - принципиальная схема апериодического звена I-го порядка
Подавая на вход звена синусоидальное напряжение амплитудой 10В и изменяя частоту этого напряжения от 1Гц до 20кГц, производим замеры амплитуды выходного сигнала и величины фазового сдвига.
Для вычисления величины фазового сдвига воспользуемся формулой
 ,
где  - частота входного сигнала;  - сдвиг фаз во времени;
Результаты измерения заносим в таблицу Таблицу 1.
Таблица 1 - Результаты измерений
 |
0,001 |
0,02 |
0,08 |
0,15 |
0,4 |
0,8 |
1 |
1,2 |
3 |
5 |
10 |
20 |
|
6,28 |
125,6 |
502,4 |
942 |
2512 |
5024 |
6280 |
7536 |
18840 |
31400 |
62800 |
125600 |
 |
-10,35 |
-10,28 |
-9.54 |
-8 |
-4,65 |
-2,75 |
-2,24 |
-1,9 |
-0,803 |
-0,49 |
-0,248 |
-0,125 |
 |
-0,37 |
-7,4 |
-27,48 |
-43,2 |
-67 |
-79,2 |
-80,64 |
-82 |
-86,72 |
-88,2 |
-89,3 |
-89,99 |
 |
10 |
 |
10 |
9,9 |
8,87 |
7,14 |
3,53 |
1,86 |
1,49 |
1,25 |
0,5 |
0,3 |
0,151 |
0,075 |
 |
1 |
0,99 |
0,87 |
0,714 |
0,353 |
0,186 |
0,149 |
0,125 |
0,05 |
0,03 |
0,015 |
0,0075 |
 |
0 |
-0,09 |
-1,2 |
-2,93 |
-9 |
-14,6 |
-16,54 |
-18 |
-26 |
-30,5 |
-36,5 |
-42,5 |
Отобразим на одном графике частотные характеристики, полученные расчетным и опытным способами.
Внешний вид амплитудно-частотной характеристики указан на Рис.6, фазо-частотной характеристики - на рис.7, логарифмических частотных характеристик - на рис.8.
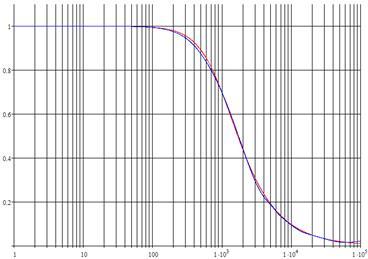
Рисунок 6 - амплитудно-частотные характеристики, полученные расчетным способом (красн) и на практике (син).
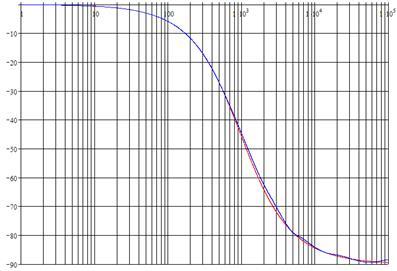
Рисунок 7 - фазо-частотные характеристики, полученные расчетным способом (красн) и на практике (син)
Рисунок 8 - логарифмические частотные характеристики, полученные расчетным способом (красн) и на практике (син).
Вывод: исследовали частотные свойства апериодического звена I-го порядка. Рассчитали его частотные характеристики теоретически и на практике.
|
