| Министерство образования и науки Республики Казахстан
Карагандинский государственный технический университет
Кафедра САПР
курсовая работа
по дисциплине: математическое обеспечение САПР
Тема: "Сравнительный анализ численных методов"
Караганда, 2009
Содержание
Введение
1. Итерационные методы решения нелинейных уравнений
1.1 Метод хорд
1.2 Практическое применение метода хорд
1.3 Метод касательных
1.4 Практическое применение метода касательных
1.4.1 Исследование функции 
1.4.2 Исследование функции 
1.5 Метод простой итерации
1.6 Практическое применение метода простой итерации
1.6.1 Исследование функции 
1.6.2 Исследование функции 
2. Решение нелинейных уравнений методом интерполирования
2.1 Многочлен Лагранжа
2.2 Интерполяция сплайнами
2.3 Практическое применение метода интерполяции для решения уравнений
2.4 Практическое применение кубического и глобального сплайна
3. Итерационные методы решения системы линейных алгебраических уравнений
3.1 Метод простой итерации
3.2 Метод Зейделя
3.3 Практическое применение метода простых итераций при решении СЛАУ
3.4 Практическое применение метода Зейделя при решении СЛАУ
3.5 Программная реализация итерационных методов решения СЛАУ
4. Сравнительный анализ различных методов численного дифференцирования и интегрирования
4.1 Методы численного дифференцирования
4.2 Методы численного интегрирования
5. Численные методы решения обыкновенных дифференциальных уравнений
5.1 Метод Эйлера
5.2 Модификация метода Эйлера:
усовершенствованный метод Эйлера
5.3 Практическое применение метода Эйлера
5.4 Практическое применение уточненного метода Эйлера
Заключение
Список используемой литературы
Целью нашей работы является сравнительный анализ численных методов, таких как итерация, интерполяция, численное дифференцирование и интегрирование, а также метод Эйлера.
В настоящее время появилось значительное число различных программных продуктов (MathCAD, MathLAB и т.д.), с помощью которых, задавая только входные данные, можно решить значительное число задач.
Для более глубокого анализа численных методов очень удобно использовать средства MathCAD, а также алгоритмические языки программирования.
Задание:
По итерационным методам решения нелинейных уравнений:
Определить корень в заданном или выбранном отрезке методом хорд, касательных и простой итерации.
Используя результаты решений, указать наименьший полученный отрезок, в котором содержится корень уравнения.
Для каждого метода и каждой задачи построить график функции  на [a,
b]
и убедиться в выполнении условия сходимости итерационной процедуры. на [a,
b]
и убедиться в выполнении условия сходимости итерационной процедуры.
Используя функции F (
x)
из п.1, построить интерполяционный многочлен L4
(
x)
на [a,
b],
использовав в качестве узловых a
и b,
остальные необходимые узловые точки выбрать, разделив промежуток [a,
b]
на почти равные части. Вычислить значения F (
x)
и L4
(
x)
в двух точках, одна из которых - середина крайней части, а вторая - середина части, содержащей точку  . Сравнить полученные величины. Используя эти же узловые точки, провести обратную интерполяцию и определить значение х
при y=0
. Полученный результат сравнить с ранее найденным решением уравнения. . Сравнить полученные величины. Используя эти же узловые точки, провести обратную интерполяцию и определить значение х
при y=0
. Полученный результат сравнить с ранее найденным решением уравнения.
Сравнить результаты решения СЛАУ методом простой итерации и методом Зейделя на различных шагах итерации.
Провести сравнительный анализ различных методов численного дифференцирования и интегрирования.
Найти численное решение обыкновенного дифференциального уравнения методом Эйлера и уточненным методом Эйлера с 5-ю и 20-ю шагами и сравнить их, если возможно с результатом точного решения ОДУ.
Задача нахождения корней нелинейных уравнений вида F (
x) =0
, где F (
x)
- непрерывная функция, - встречается в различных областях научных исследований. Корнам (или решением) уравнения F (
x) =0
называется значение  , при котором , при котором . Методы решения нелинейных уравнений делятся на: . Методы решения нелинейных уравнений делятся на:
прямые;
итерационные.
Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Такие методы применяются для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.
Однако, на практике встречаются уравнения, которые не удается решить простыми методами. Тогда используются итерационные методы решения, т.е. методы последовательных приближений.
Алгоритм нахождения корня нелинейного уравнения с помощью итерационного метода состоит из двух этапов:
этап локализации (или отделения) корней;
этап итерационного уточнения.
Локализация корней. Отрезок [a, b], содержащий только один корень  уравнения F (
x) =0
, называют отрезком локализации корня уравнения F (
x) =0
, называют отрезком локализации корня  . Цель этапа локализации считают достигнутой, если для каждого из подлежащих определению корня удалось указать отрезок локализации (его длину по возможности стараются сделать минимальной). Прежде чем переходить к отыскиванию отрезков локализации, имеет смысл провести предварительное исследование задачи для выяснения того, существует ли вообще корни уравнения и как они расположены на числовой оси. Начальное приближение может быть найдено различными способами: из физических соображений, с помощью графических методов и т.д. Если оценку исходного приближения провести не удается, то находят две близко расположенные точки a
и b
, в которых непрерывная функция F (
x)
принимает значения разных знаков, т.е. F (
a)
F (
b) <0
. При выполнении этого условия, можно говорить, что между точками a
и b
есть, по крайней мере, одна точка, в которой F (
x) =0
. . Цель этапа локализации считают достигнутой, если для каждого из подлежащих определению корня удалось указать отрезок локализации (его длину по возможности стараются сделать минимальной). Прежде чем переходить к отыскиванию отрезков локализации, имеет смысл провести предварительное исследование задачи для выяснения того, существует ли вообще корни уравнения и как они расположены на числовой оси. Начальное приближение может быть найдено различными способами: из физических соображений, с помощью графических методов и т.д. Если оценку исходного приближения провести не удается, то находят две близко расположенные точки a
и b
, в которых непрерывная функция F (
x)
принимает значения разных знаков, т.е. F (
a)
F (
b) <0
. При выполнении этого условия, можно говорить, что между точками a
и b
есть, по крайней мере, одна точка, в которой F (
x) =0
.
Итерационное уточнение корней. На этом этапе для вычисления каждого из корней с точностью  используют тот или иной итерационный метод, позволяющий построить последовательность х1
, х2
, х3
, …,
х
k,
… приближений к корню используют тот или иной итерационный метод, позволяющий построить последовательность х1
, х2
, х3
, …,
х
k,
… приближений к корню  .
Итерационный процесс состоит в последовательном уточнении начального приближения х0
. Каждый такой шаг называется итерацией
. В результате итераций находится последовательность приближенных значений корня х1
, х2
, х3
, …,
х
k,
…
Если эти значения с ростом k
стремятся к истинному значению корня .
Итерационный процесс состоит в последовательном уточнении начального приближения х0
. Каждый такой шаг называется итерацией
. В результате итераций находится последовательность приближенных значений корня х1
, х2
, х3
, …,
х
k,
…
Если эти значения с ростом k
стремятся к истинному значению корня  , то говорят, итерационный процесс сходится
. , то говорят, итерационный процесс сходится
.
Пусть мы нашли отрезок [a,
b],
на котором функция F (
x)
меняет знак. Для определенности примем F (
a) >0,
F (
b) <0.
В данном методе процесс итераций состоит в том, что в качестве приближений корню уравнения принимаются значения х0
, х1
,… точек пересечения хорды с осью абсцисс.
Сначала найдем уравнение хорды АВ:
 
Для точки пересечения ее с осью абсцисс (y=0
) получим уравнение
 . .
Далее, сравнивая знаки величин F (
a)
и F (
x)
для рассматриваемого случая, приходим к выводу, что корень находится в интервале (a,
x),
так как F (
a)
*F (
x) <0 (
условие существование корня). Отрезок [x,
b]
отбрасываем и больше не рассматриваем. Следующая итерация состоит в определении нового приближения xn
как точки пересечения хорды АВ1
с осью абсцисс и так далее. На рисунке 1 изображена геометрическая интерпретация нахождение решения методом хорд.
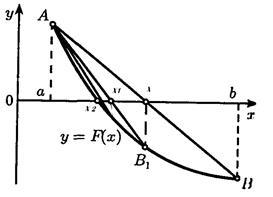
Рисунок 1 - Метод хорд
При решении уравнения методом хорд поводится прямая соединяющая концы отрезка [a,b].
Из двух точек А
и В
выбирается х0
. Находится точка пересечения хорды с осью OX. Определяется значение функции в точке пересечения и из найденной точки проводится новая хорда. Этот процесс повторяется до получения необходимой точности.
Формула для n-го приближения имеет вид (х0
=а,
xn
-1
=
b,
xn
=
x):

В методе хорд условием окончания итераций является:
условие близости двух последовательных приближений:  ; ;
условие малости невязки  (величина F (
xn
)
есть невязка, полученная на n
-й итерации, а (величина F (
xn
)
есть невязка, полученная на n
-й итерации, а  -число, с заданной точностью которого необходимо найти решение). -число, с заданной точностью которого необходимо найти решение).
Исследование функции

Возьмем для исследования функцию  и определим точность решения как и определим точность решения как  =0,001. =0,001.

Рисунок 2 - График функции 
Визуально определяем границы отрезка, на котором находится корень. Выделяем отрезок [a,b],
(а= -0,45, b= -0,3).
1. Проверяем существование корня на отрезке по условию  : :


Убедимся, что функция принимает на концах указанных отрезков значения разных знаков



0,36<0
Условие выполнено, следовательно, на данном промежутке корень есть.
2. Далее исследуем функцию на монотонность:




75.1115>0
Экстремумов на выбранном отрезке нет.
3. Проверяем функцию на единственность корня





67.86>0
На данном промежутке имеется только один корень
4. Выбор точки х0
зависит от того совпадает ли её знак со знаком второй производной данной функции.

 >0 >0
Из условия следует, что х0
=
a=-0.45
, тогда за х1
принимаем b - х1
= b=-0.3


5. Исходя из графика мы приняли за x0
=-0.45 и
x1
=-0.3
. Найдем значение функции в этих точках:


Формула для решения

 



 



 




Условие выполнено, необходимая точность достигнута. Итерационный процесс можно прекратить. Добиться указанной точности нам удалось на 4-ой проведенной итерации.
Исследование функции

Возьмем для исследования функцию  и определим точность решения как и определим точность решения как  =0,001. =0,001.

Рисунок 3 - График функции 
Визуально определяем границы отрезка, на котором находится корень. Выделяем отрезок [a,b],
(а=-0,4, b=0,1).
1. Проверяем существование корня на отрезке по условию  : :

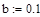
Убедимся, что функция принимает на концах указанных отрезков значения разных знаков



0,04327
<0
Условие выполнено, следовательно, на данном промежутке корень есть.
2. Далее исследуем функцию на монотонность:
 



Экстремумов на выбранном отрезке нет.
3. Проверяем функцию на единственность корня:




  >0 >0
На данном промежутке имеется только один корень.
4) Выбор точки х0
зависит от того совпадает ли её знак со знаком второй производной данной функции.

 >0 >0
Из условия следует, что х0
=
a=-0.4
, тогда за х1
принимаем b - х1
=
b=0.1


5. Исходя из графика мы приняли за x0=-0.4 и
x1=0.1
. Найдем значение функции в этих точках:

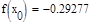
Формула для решения

 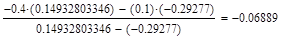



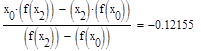 



 



 



 




Условие выполнено, необходимая точность достигнута. Итерационный процесс можно прекратить. Добиться указанной точности нам удалось на 6-ой проведенной итерации.
Его отличие от предыдущего метода состоит в том, что на k
-й итерации вместо хорды проводится касательная к кривой y=
F (
x)
при х=
ck
-1
и ищется точка пересечения касательной с точкой абсцисс. При этом необязательно задавать отрезок [a,
b],
содержащий корень уравнения, а достаточно лишь найти некоторое начальное приближение корнях.

Рисунок 4 - Метод касательных
Уравнение касательной, проведенной к кривой y=
F (
x)
в некоторой точке с координатами х0
и F (х0
)
имеет вид:
y-
F (х0
) =
F’ (х0
) (
x-х0
).
Отсюда найдем следующее приближение корня х
как абсциссу точки пересечения касательной с осью х (у=0):
х=х0
-
F (х0
) /
F’ (х0
).
Аналогично могут быть найдены и следующие приближения как точки пересечения с осью абсцисс касательных. Формула для n-го приближения имеет вид:
х
n
=х
n-1
-
F (х
n-1
) /
F’ (х
n-1
),
n=1,2,…
При этом необходимо, чтобы выполнялось условие F’ (х
n-1
)  0. 0.
Для окончания итерационного процесса используются те же условия, что и в методе хорд.
Решим уравнение  методом касательных: методом касательных:

Рисунок 5 - График функции 
Применим формулы:
хn
=хn-1
- F (хn-1
) /F’ (хn-1
) и 


Первая производная от функции:



9,308
>0
Вторая производная от функции:



8,7
<0
В качестве х0
выбрали а
из условия, что значение функции в этой точке имеет такой же знак как и у второй производной на отрезке.


Применим формулу:

 =0,001. =0,001.







0,0428
>0.001







Условие выполнено, необходимая точность достигнута. Итерационный процесс можно прекратить. Добиться указанной точности нам удалось на 2-ой проведенной итерации.

Рисунок 6 - График  для функции для функции 
Говоря о функции х= , - выбрав начальное приближение х0
строится последовательность хп
стремящаяся к , - выбрав начальное приближение х0
строится последовательность хп
стремящаяся к  и условием сходимости здесь является и условием сходимости здесь является  , т.е. тангенс угла наклона касательной должен быть меньше 1 (угол должен составлять менее 45 градусов). , т.е. тангенс угла наклона касательной должен быть меньше 1 (угол должен составлять менее 45 градусов).
Решим уравнение 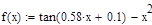 методом касательных: методом касательных:

Рисунок 7 - График функции 


Первая производная от функции
 : :


1,39
>0
Вторая производная от функции
 : :


2.091<0
В качестве х0 выбрали а
из условия, что значение функции в этой точке имеет такой же знак как и у второй производной на отрезке.


Применим формулу:

 =0,001. =0,001.







0,2106
>0.001






0.0477>0.001






0.0026>0.001







Условие выполнено, необходимая точность достигнута. Итерационный процесс можно прекратить. Добиться указанной точности нам удалось на 4-ой проведенной итерации.
Как мы видим, на каждой итерации объем вычислений в методе касательных больший, чем в методе хорд, так как приходится находить не только функции F (х),
но и их производные. Однако скорость сходимости значительно выше в методе касательных.
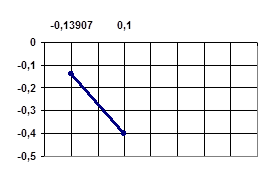
Рисунок 8 - График  функции функции 
Говоря о функции х= , - выбрав начальное приближение х0
строится последовательность хп
стремящаяся к , - выбрав начальное приближение х0
строится последовательность хп
стремящаяся к  и условием сходимости здесь является и условием сходимости здесь является  , т.е. тангенс угла наклона касательной должен быть меньше 1 (угол должен составлять менее 45 градусов). , т.е. тангенс угла наклона касательной должен быть меньше 1 (угол должен составлять менее 45 градусов).
Теорема о сходимости метода простой итерации. Пусть в некоторой  - окрестности корня - окрестности корня  функция функция  дифференцируема и удовлетворяет неравенству дифференцируема и удовлетворяет неравенству  , где , где  - постоянная. Тогда независимо от выбора начального приближения из указанной - постоянная. Тогда независимо от выбора начального приближения из указанной  - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится со скоростью геометрической последовательности и справедлива оценка погрешности: - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится со скоростью геометрической последовательности и справедлива оценка погрешности:
 , ,  . .
Критерий окончания итерационного процесса. При заданной точности  >0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство >0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство

Если величина  , то можно использовать более простой критерий окончания итераций: , то можно использовать более простой критерий окончания итераций:

Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду:

Предположим дополнительно, что производная  знакопостоянна и знакопостоянна и  на отрезке [a,b].
Тогда при выборе итерационного параметра на отрезке [a,b].
Тогда при выборе итерационного параметра
 , ,
метод сходится и значение


Рисунок 9 - График функции 
Будем искать простой корень уравнения, находящийся на отрезке локализации [-0.45,-0.3]:




Найдем корень с помощью встроенной функции root
:


Приведем уравнение к виду x= (x),
где

Проверим условие сходимости:

Максимальное по модулю значение производной итерационной функции достигается в левом конце отрезка:



Выполним итерации по расчетной формуле x= (x):
  
  
  
  
  
  
Погрешность найденного значения:

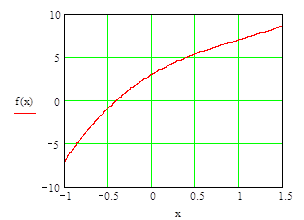
Рисунок 10 - График функции 
Приведем уравнение к виду x=x-f (x),
где итерационная функция (x) =x-f (x),
- итерационный параметр.


Максимальное и минимальное значения производной достигаются на концах отрезка:
  ; ;  
 
 
 
Выполним итерации по расчетной формуле
x= (x) =x - f (x)):

  
  
  
Погрешность найденного значения:

Программная реализация итерационных методов

Рисунок 11 - Решение уравнения методом касательных и методом хорд
Интерполяция является одним из способов аппроксимации функции. Смысл аппроксимации заключается в том, что одна функция заменяется другой в некотором смысле близкой. Такая задача возникает по многим соображениям, в частности из-за удобства вычисления значений функции, вычисления производных и т.д.
Пусть в точках  расположенных на отрезке [a, b] и попарно различных, задана таблица значений некоторой функции расположенных на отрезке [a, b] и попарно различных, задана таблица значений некоторой функции  . Задача интерполяции состоит в построении функции φ (х), удовлетворяющей условию . Задача интерполяции состоит в построении функции φ (х), удовлетворяющей условию  . При этом предполагается, что среди значений . При этом предполагается, что среди значений  нет одинаковых, т.е. нет одинаковых, т.е.  при при  . Другими словами, ставиться задача о построении функции φ (х), график которой проходит через заданные точки . Другими словами, ставиться задача о построении функции φ (х), график которой проходит через заданные точки  . Указанный способ приближения функции принято называть интерполяцией (или интерполированием), а точки . Указанный способ приближения функции принято называть интерполяцией (или интерполированием), а точки  - узлами интерполяции. - узлами интерполяции.
Значение функции 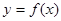 вычисляется, когда известны функция f. Но эти значения могут быть получены, например экспериментальным путем, как значение некой неизвестной функции. вычисляется, когда известны функция f. Но эти значения могут быть получены, например экспериментальным путем, как значение некой неизвестной функции.

Рисунок 12 - Интерполяция
Таким образом, близость интерполирующей функции (сплошная линия) к заданной функции состоит в том, что их значения совпадают на заданной системе точек. Интерполирующая функция φ (х) может строиться сразу для всего рассматриваемого интервала измерения х или отдельно для разных частей этого интервала. В первом случае говорят о глобальной интерполяции, во втором - о кусочной (или локальной) интерполяции.
Рассмотрим случай глобальной интерполяции, т.е. построение интерполяционного многочлена, единого для всего отрезка  . .
Будем искать интерполяционный многочлен в виде линейной комбинации многочленов степени n
:

При этом потребуем, чтобы каждый многочлен  обращался в нуль во всех узлах интерполяции, за исключением одного (i
-го), где он должен равняться единице. Этим условиям при i=0
отвечает многочлен вида: обращался в нуль во всех узлах интерполяции, за исключением одного (i
-го), где он должен равняться единице. Этим условиям при i=0
отвечает многочлен вида:
 . .
По аналогии получим:
 , ,
 , ,
 , ,

Подставляя полученные выражения в
 , находим: , находим:
 . .
Эта формула определяет интерполяционный многочлен Лагранжа.
Обратное интерполирование заключается в установлении зависимости  . .
Задача обратного интерполирования заключается в том, чтобы по заданному значению функции y
определить соответствующее значение аргумента x
.
Функция выглядит следующим образом:
Ln
(
y) =
Повышение точности приближения гладкой функции благодаря увеличению степени интерполяционного многочлена возможно, но связано с существенным повышением сложности вычисления. К тому же использование многочленов высокой степени требует специальных мер предосторожности уже при выборе формы их записи, и вычисления сопровождаются накоплением ошибок округления.
Поэтому на практике предпочитают кусочно-полиномиальную интерполяцию с использованием многочленов невысокой степени. Однако этот способ приближения имеет недостаток: в точках "стыка" двух соседних многочленов производная, как правило, имеет разрыв. Часто это обстоятельство не играет существенной роли. Вместе с тем нередко требуется, чтобы аппроксимирующая функция была гладкой и тогда простейшая кусочно-полиномиальная интерполяция становится неприемлемой.
Естественная потребность в наличии аппроксимирующих функций, которые сочетали бы в себе локальную простоту многочлена невысокой степени и глобальную на всем отрезке [a, b] гладкость, привела к появлению в 1946 г. так называемых сплайн - функций
или сплайнов -
специальным образом построенных гладких кусочно-многочленных функций. Получив в 60-х годах распространение как средство интерполяции сложных кривых, сплайны к настоящему времени стали важной составной частью самых различных вычислительных методов, и нашли широчайшее применение в решении разнообразных научно-технических и инженерных задач.
Дадим строгое определение сплайна. Пусть отрезок [a, b] разбит точками  на n
частичных отрезков на n
частичных отрезков  . Сплайном степени т
называется функция
. Сплайном степени т
называется функция  ,
обладающая следующими свойствами: ,
обладающая следующими свойствами:
функция  непрерывна на отрезке [a, b] вместе со всеми своими производными
непрерывна на отрезке [a, b] вместе со всеми своими производными  до некоторого порядка р
, до некоторого порядка р
,
на каждом частичном отрезке  функция
функция  совпадает с некоторым алгебраическим многочленом
совпадает с некоторым алгебраическим многочленом  степени m
.
степени m
.
Разность т - р
между степенью сплайна и наивысшим порядком непрерывной на отрезке [a, b] производной называется дефектом сплайна.
Простейший пример сплайна дает непрерывная кусочно-линейная функция (рисунок 13), являющаяся сплайном первой степени (линейным сплайном)
с дефектом, равным единице. Действительно, на отрезке [a, b] сама функция  (
нулевая производная) непрерывна. В то же время на каждом частичном отрезке (
нулевая производная) непрерывна. В то же время на каждом частичном отрезке  совпадает с некоторым многочленом первой степени.
совпадает с некоторым многочленом первой степени.
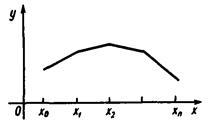 
Рисунок 13 - Кусочно-линейная функция
Наиболее широкое распространение на практике получили сплайны  третьей степени (кубические сплайны)
с дефектом, равным 1 или 2. Такие сплайны на каждом из частичных отрезков [
третьей степени (кубические сплайны)
с дефектом, равным 1 или 2. Такие сплайны на каждом из частичных отрезков [ ] совпадают с кубическим многочленом: ] совпадают с кубическим многочленом:

и имеют на отрезке [a, b] по крайней мере одну непрерывную производную  . .
Формула кубического сплайна:

Полученный кубический сплайн в этом случае, очевидно, что не прерывен с первой производной, но непрерывность второй производной не гарантируется, т.е. дефект интерполяционного сплайна = 2. Если этот сплайн имеет непрерывную вторую производную на отрезке [a, b], т.е. имеет дефект 1, то такой сплайн носит название глобального.
Для построения глобального сплайна, т.е. сплайна с дефектом 1, необходимо начинать со второго узла, поставить условия непрерывности второй производной, т.е. вторая производная при подходе к точке 2 и дальше с лева (х1-0) должен равняться второй производной при подходе справа (х1+0). Такие равенства можем составить для всех внутренних узлов начиная с х1 до хn-1. Затем используем условия на края х0 и хn. Получим систему уравнений, которые и обеспечат дефект 1.

Очевидно, что при наличии S3 на соответствующих узлах, построение таких равенств не представляет особого труда.
 
Прировняв эти значения для определения m получим СЛАУ.
 
В двух крайних точках определяется i производных 
Если функция задана ввиде таблиц, то для вычисления производныхиспользуеться результаты полученные при численном диференцировании порядок точности которых не ниже 3-ей степени.
Для исследования была взята функция: 
Выберем значения узлов на отрезке [b, b+2] интерполяции и найдем значения функции в узлах:






В качестве X1
возьмем точку между первым и вторым узлом:

Строим интерполяционный многочлен:



В качестве Х2
возьмем точку между четвертым и пятым узлом:


Строим интерполяционный многочлен:












Построим график функции и интерполяционного многочлена:


Рисунок 14 - График функции и интерполяционного многочлена
Данный результат очень близок к найденным раннее решениям, методом хорд, касательных и простых итераций и совпадает с ними. Используя эти же узловые точки проведем обратную интерполяцию и определим значение х при у=0.













Исследуем функцию:
 ; ; 
Дефект 
Значение функции в этих точках: 
Производная функции: 
Значение производной в этих точках:

Используя формулу кубического сплайна получим:

 

 

Рисунок 15 - График функции и кубического сплайна
Используя формулу глобального сплайна получим:
 



Рисунок 16 - График функции и кубического и глобального сплайна
К решению систем линейных уравнений сводятся многочисленные практические задачи. Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики. Методы решения линейных уравнений делятся на две группы - прямые и итерационные. Прямые методы используют конечные соотношения для вычисления неизвестных. Они дают решение после выполнения заранее известного числа операций. Эти методы сравнительно просты и наиболее универсальны. Но вместе с тем эти методы имеют ряд недостатков. Как правило, они требуют хранения в оперативной памяти компьютера сразу всей матрицы, и при больших значениях расходуется много места в памяти. Существенным недостатком прямых методов является также накапливание погрешностей в процессе решения, поскольку вычисления на любом этапе используют результаты предыдущих операций.
Итерационные методы в этом отношении предпочтительнее. Они требуют хранения в памяти машины не всей матрицы системы, а лишь нескольких векторов с n
компонентами. Погрешности окончательных результатов при использовании итерационных методов не накапливаются, поскольку точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений. К итерационным методам относят метод простой итерации, метод Зейделя.
Этот метод широко используется для численного решения уравнений и их систем различных видов. Рассмотрим применение метода простой итерации к решению систем линейных уравнений.
Запишем исходную систему уравнений в векторно-матричном виде  и выполним ряд тождественных преобразований: и выполним ряд тождественных преобразований:

Где  - некоторое число, Е - единичная матрица, - некоторое число, Е - единичная матрица,  . .
Получившаяся система эквивалентна исходной системе и служит основой для построения метода простой итерации.
Выберем некоторое начальное приближение  и поставим в правую часть системы: и поставим в правую часть системы:

Поскольку  не является решением системы, в левой части получится некоторый столбец не является решением системы, в левой части получится некоторый столбец  , в общем случае отличный от , в общем случае отличный от  . Полученный столбец . Полученный столбец  будем рассматривать в качестве следующего (первого) приближения к решению. Аналогично, по известному k
-му приближению можно найти (k+1) - е приближение: будем рассматривать в качестве следующего (первого) приближения к решению. Аналогично, по известному k
-му приближению можно найти (k+1) - е приближение:

Эта формула и выражает собой метод простой итерации. Для ее применения нужно задать неопределенный пока параметр  . От значения . От значения  зависит, будет ли сходится метод, а если будет, то какова будет скорость сходимости
, т.е. как много итераций нужно совершить для достижения требуемой точности. В частности справедлива следующая теорема. зависит, будет ли сходится метод, а если будет, то какова будет скорость сходимости
, т.е. как много итераций нужно совершить для достижения требуемой точности. В частности справедлива следующая теорема.
Теорема.
Метод простой итерации сходится тогда и только тогда, когда все собственные числа матрицы  по модулю меньше единицы. по модулю меньше единицы.
Для некоторых типов матрицы А можно указать правило выбора  , обеспечивающее сходимость метода и оптимальную скорость сходимости. В простейшем случае , обеспечивающее сходимость метода и оптимальную скорость сходимости. В простейшем случае  можно положить равным некоторому постоянному числу, например, 1, 0.1 и т.д. можно положить равным некоторому постоянному числу, например, 1, 0.1 и т.д.
Этот метод можно проиллюстрировать на примере решения системы:
a11
x1
+a12
x2
+a13
x3
=b1
a21
x1
+a22
x2
+a23
x3
=b2
a31
x1
+
a32
x2
+
a33
x3
=
b3
Предположим, что диагональные элементы a11
, a
22
, a
33
отличны от нуля (в противном случае можно переставить уравнения). Выразим неизвестные х1
, х2
, х3
соответственно из первого, второго и третьего уравнений системы:

Зададим некоторые начальные (нулевые) приближения значений неизвестных: х1
=х1
(0),
х2
=х2
(0),
х3
=х3
(0).
Подставляя эти значения в правую часть выражения (‘1), получаем новое (первое) приближение для х1
:

Используя это значение для х1
и приближение х3
(0)
для х3
, находим из (‘2) первое приближение для х2
:
 . .
И наконец, используя вычисленные значения х1
=х1
(1),
х2
=х2
(1),
находим с помощью выражения (‘3) первое приближение для х3
:

На этом заканчивается первая итерация решения системы (‘1) (‘2) (‘3). Используя теперь значения х1
(1),
х2
(1),
х3
(1),
можно таким же способом провести вторую итерацию, в результате которой будут найдены вторые приближения к решению х1
=х1
(2),
х2
=х2
(2),
х3
=х3
(2)
и т.д.
Приближение с номером с k
можно вычислить, зная приближение с номером k-1
, как

Итерационный процесс продолжается до тех пор, пока значения х1
(
k),
х2
(
k),
х3
(
k)
не станут близкими с заданной погрешностью к значениям х1
(
k-1),
х2
(
k-1),
х3
(
k-1).
Решим систему линейных уравнений методом простых итераций с точностью равной  . .

Выполним проверку на условие сходимости:


Условие выполнено, можно приступать к вычислению нулевого шага:




Начнем итерационный процесс:
















Проверим выполняется ли условие остановки итерационного процесса: 

Сходимость в сотых долях имеет место уже на 4-ом шаге, тогда можно принять:

Решим ту же систему линейных уравнений методом Зейделя с той же точностью:  . .

Проверку на условие сходимости мы выполнили ранее, при решении методом простых итерации.











Условие сходимости выполнено на 3-ем шаге.
Корнями уравнения можно принять:


Рисунок 17 - Решение системы уравнений методом простых итераций.

Рисунок 18 - Решение уравнения методом Зейделя
Необходимость численного дифференцирования может возникнуть при необходимости исследований функций заданных табличным образом, кроме тех случаев, когда вычисление производной численно может оказаться проще, чем дифференцирование. Предположим, что в окрестности точки xi
функция F (x) дифференцируема достаточное число раз. Исходя из определения производной:

используем для её вычисления две приближенные формулы:
 (1) (1)
 (2) (2)
Формулы (1) и (2) называют правыми и левыми разностными производными.
Для оценки погрешностей формул численного дифференцирования используется формула Тейлора:

откуда можно вычислить:
 (3) (3)
Выражение (3) имеет погрешность порядка (x-xi
), следовательно, формулы правых и левых разностных производных имеют погрешность одного порядка с h, где h=xi
-xi
-1
Такая точность достаточно невысока, поэтому применяется так называемая центрально-симметричная форма производной, погрешность которой одного порядка с h2
 (4) (4)
Хотя очевидно, что формула (4) используется для внутренних точек отрезка.
Для примера возьмём ряд точек:

Вычислим производную функции f (x) =sin (x) в одной из них двумя способами.
Очевидно, что h=
По центрально-симметричной формуле:

По формуле левой разностной производной:

Табличное значение  =cos ( =cos ( ) =0.8660, т.е. значение производной, полученное по центрально-симметричной формуле ближе к истинному. ) =0.8660, т.е. значение производной, полученное по центрально-симметричной формуле ближе к истинному.
В прикладных исследованиях часто возникает необходимость вычисления значения определённого интеграла

Как известно из курса математики, аналитически вычисление интеграла можно провести не во всех случаях. И даже в том случае, когда удаётся найти аналитический вид этого интеграла, процедура вычисления даёт приближённый результат, поэтому возникает задача приближенного значения этого интеграла.

Суть приближенного вычисления заключается в двух операциях: 1. в выборе конечного числа вместо n; 2. в выборе точки  в соответствующем отрезке. в соответствующем отрезке.
В зависимости от выбора  мы получаем различные формулы для вычисления интеграла: Формулы левых и правых прямоугольников (5), (6) мы получаем различные формулы для вычисления интеграла: Формулы левых и правых прямоугольников (5), (6)
 (5) (5)
 (6) (6)
Формула трапеции:

Формула Симпсона

где m=n/2
h=b-a/n
b, a - концы рассматриваемого отрезка.
Для сравнения результатов вычисления вышеизложенными формулами численного интегрирования вычислим 3-мя способами следующий интеграл, разделив отрезок [0,  ] на 6 равных отрезков: ] на 6 равных отрезков:
 h= h=
По формуле левых прямоугольников:

По формуле трапеции:

По формуле Симпсона:

А результат полученный аналитически равен
 =1 =1
Следовательно, можно сделать вывод о том, что численный метод интегрирования по формуле Симпсон является более точным, но используется в общем случае при делении рассориваемого отрезка на чётное число промежутков.
Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции y=y (x). Их можно записать в виде
 , где х - независимая переменная. , где х - независимая переменная.
Наивысший порядок n входящей в уравнение производной называется порядком дифференциального уравнения. производной называется порядком дифференциального уравнения.
Методы решения обыкновенных дифференциальных уравнений можно разбить на следующие группы: графические, аналитические, приближенные и численные.
Графические методы используют геометрические построения.
Аналитические методы встречаются в курсе дифференциальных уравнений. Для уравнений первого порядка (с разделяющимися переменными, однородных, линейных и др.), а также для некоторых типов уравнений высших порядков (например, линейных с постоянными коэффициентами) удается получить решения в виде формул путем аналитических преобразований.
Приближенные методы используют различные упрощения самих уравнений путем обоснованного отбрасывания некоторых содержащихся в них членов, а также специальным выбором классов искомых функций.
Численные методы решения дифференциальных уравнений в настоящее время являются основным инструментом при исследовании научно-технических задач, описываемых дифференциальными уравнениями. При этом необходимо подчеркнуть, что данные методы особенно эффективны в сочетании с использованием современных компьютеров.
Простейшим численным методом решения задачи Коши для ОДУ является метод Эйлера. Рассмотрим уравнение  в окрестностях узлов в окрестностях узлов  (i=1,2,3,…) и заменим в левой части производную (i=1,2,3,…) и заменим в левой части производную  правой разностью. При этом значения функции правой разностью. При этом значения функции  узлах узлах  заменим значениями сеточной функции заменим значениями сеточной функции  : :

Полученная аппроксимация ДУ имеет первый порядок, поскольку при замене  на на  допускается погрешность допускается погрешность  . .
Будем считать для простоты узлы равноотстоящими, т.е.  Тогда из равенства Тогда из равенства  получаем получаем

Заметим, что из уравнения следует следует
 . .
Поэтому  представляет собой приближенное нахождение значение функции представляет собой приближенное нахождение значение функции  в точке в точке  при помощи разложения в ряд Тейлора с отбрасыванием членов второго и более высоких порядков. Другими словами, приращение функции полагается равным её дифференциалу. при помощи разложения в ряд Тейлора с отбрасыванием членов второго и более высоких порядков. Другими словами, приращение функции полагается равным её дифференциалу.
Полагая i=0, с помощью соотношения  находим з значение сеточной функции находим з значение сеточной функции  при при  : :
 . .
Требуемое здесь значение  задано начальным условием задано начальным условием  , т.е. , т.е.
 . .
Аналогично могут быть найдены значения сеточной функции в других узлах:

Построенный алгоритм называется методом Эйлера

Рисунок - 19 Метод Эйлера
Геометрическая интерпретация метода Эйлера дана на рисунке. Изображены первые два шага, т.е. проиллюстрировано вычисление сеточной функции в точках  . Интегральные кривые 0,1,2 описывают точные решения уравнения . Интегральные кривые 0,1,2 описывают точные решения уравнения  . При этом кривая 0 соответствует точному решению задачи Коши, так как она проходит через начальную точку А (x0
,y0
). Точки B,C получены в результате численного решения задачи Коши методом Эйлера. Их отклонения от кривой 0 характеризуют погрешность метода. При выполнении каждого шага мы фактически попадаем на другую интегральную кривую. Отрезок АВ - отрезок касательной к кривой 0 в точке А, ее наклон характеризуется значением производной . При этом кривая 0 соответствует точному решению задачи Коши, так как она проходит через начальную точку А (x0
,y0
). Точки B,C получены в результате численного решения задачи Коши методом Эйлера. Их отклонения от кривой 0 характеризуют погрешность метода. При выполнении каждого шага мы фактически попадаем на другую интегральную кривую. Отрезок АВ - отрезок касательной к кривой 0 в точке А, ее наклон характеризуется значением производной . Погрешность появляется потому, что приращение значения функции при переходе от х0
к х1
заменяется приращением ординаты касательной к кривой 0 в точке А. Касательная ВС уже проводится к другой интегральной кривой 1. таким образом, погрешность метода Эйлера приводит к тому, что на каждом шаге приближенное решение переходит на другую интегральную кривую. . Погрешность появляется потому, что приращение значения функции при переходе от х0
к х1
заменяется приращением ординаты касательной к кривой 0 в точке А. Касательная ВС уже проводится к другой интегральной кривой 1. таким образом, погрешность метода Эйлера приводит к тому, что на каждом шаге приближенное решение переходит на другую интегральную кривую.
Рассмотрим уравнение  в окрестностях узлов в окрестностях узлов  . В левой части уравнения . В левой части уравнения  заменим производную центральной разностью заменим производную центральной разностью
 , ,
а правую часть оставим без изменений:
 . .
Приближенное значение функции  в точке в точке  вычислим с помощью метода Эйлера: вычислим с помощью метода Эйлера:
 . .
Выразим  из из
 , ,
заменив  его приближением его приближением  : :

Данный метод имеет второй порядок точности.
Исходное ОДУ:

y (1,8) =2,6, 
Таблица 1. метод Эйлера (n=5)
| i
|
xi
|
yi+1
|
f (xi
,yi
)
|
h*f (xi
,yi
)
|
| 0
|
1,8
|
3.0393624
|
2.1968119
|
0.4393624
|
| 1
|
2
|
3.4813579
|
2.2099777
|
0.4419955
|
| 2
|
2,2
|
3.9241350
|
2.2138853
|
0.4427771
|
| 3
|
2,4
|
4.3675167
|
2.2169085
|
0.4433817
|
| 4
|
2,6
|
4.8128840
|
2.2268365
|
0.4453673
|
| 5
|
2,8
|
5.2630132
|
2.2506461
|
0.4501292
|
Таблица 2. метод Эйлера (n=20)
| i
|
xi
|
yi+1
|
f (xi
,yi
)
|
h*f (xi
,yi
)
|
| 0
|
1,8
|
2.7098405952
|
2.1968119048
|
0.1098405952
|
| 1
|
1,85
|
2.8199037007
|
2.2012621087
|
0.1100631054
|
| 2
|
1,9
|
2.9301422065
|
2.2047701167
|
0.1102385058
|
| 3
|
1,95
|
3.0405154109
|
2.2074640873
|
0.1103732044
|
| 4
|
2
|
3.1509890866
|
2.2094735145
|
0.1104736757
|
| 5
|
2,05
|
3.2615355030
|
2.2109283275
|
0.1105464164
|
| 6
|
2,1
|
3.3721334073
|
2.2119580866
|
0.1105979043
|
| 7
|
2,15
|
3.4827679715
|
2.2126912836
|
0.1106345642
|
| 8
|
2,2
|
3.5934307091
|
2.2132547518
|
0.1106627376
|
| 9
|
2,25
|
3.7041193685
|
2.2137731878
|
0.1106886594
|
| 10
|
2,3
|
3.8148378077
|
2.2143687841
|
0.1107184392
|
| 11
|
2,35
|
3.9255958562
|
2.2151609716
|
0.1107580486
|
| 12
|
2,4
|
4.0364091696
|
2.2162662661
|
0.1108133133
|
| 13
|
2,45
|
4.1472990802
|
2.2177982138
|
0.1108899107
|
| 14
|
2,5
|
4.2582924517
|
2.2198674293
|
0.1109933715
|
| 15
|
2,55
|
4.3694215376
|
2.2225817186
|
0.1111290859
|
| 16
|
2,6
|
4.4807238516
|
2.2260462796
|
0.1113023140
|
| 17
|
2,65
|
4.5922420502
|
2.2303639716
|
0.1115181986
|
| 18
|
2,7
|
4.7040238326
|
2.2356356483
|
0.1117817824
|
| 19
|
2,75
|
4.8161218599
|
2.2419605453
|
0.1120980273
|
| 20
|
2,8
|
4.9285936957
|
2.2494367159
|
0.1124718358
|

Таблица 3. метод Эйлера (n=5)
| i
|
xi
|
yi
|
f (xi
,yi
)
|
h*f (xi
,yi
)
|
| 0
|
1,8
|
3.0408296
|
2.1968119
|
0.1098406
|
| 1
|
2
|
3.5034503
|
2.2093361
|
0.1104668
|
| 2
|
2,2
|
3.9875064
|
2.2040057
|
0.1102003
|
| 3
|
2,4
|
4.4928015
|
2.1891243
|
0.1094562
|
| 4
|
2,6
|
5.0193000
|
2.1754674
|
0.1087734
|
| 5
|
2,8
|
5.5671264
|
2.1759596
|
0.1087980
|
Таблица 4. метод Эйлера (n=20)
| i
|
xi
|
yi
|
f (xi
,yi
)
|
h*f (xi
,yi
)
|
| 0
|
1,8
|
2.7099548
|
2.1968119
|
0.1098406
|
| 1
|
1,85
|
2.8213531
|
2.2012143
|
0.1100607
|
| 2
|
1,9
|
2.9341858
|
2.2041527
|
0.1102076
|
| 3
|
1,95
|
3.0484445
|
2.2057163
|
0.1102858
|
| 4
|
2
|
3.1641214
|
2.2060049
|
0.1103002
|
| 5
|
2,05
|
3.2812091
|
2.2051292
|
0.1102565
|
| 6
|
2,1
|
3.3997009
|
2.2032109
|
0.1101605
|
| 7
|
2,15
|
3.5195904
|
2.2003825
|
0.1100191
|
| 8
|
2,2
|
3.6408721
|
2.1967877
|
0.1098394
|
| 9
|
2,25
|
3.7635409
|
2.1925804
|
0.1096290
|
| 10
|
2,3
|
3.8875922
|
2.1879256
|
0.1093963
|
| 11
|
2,35
|
4.0130221
|
2.1829984
|
0.1091499
|
| 12
|
2,4
|
4.1398272
|
2.1779839
|
0.1088992
|
| 13
|
2,45
|
4.2680046
|
2.1730767
|
0.1086538
|
| 14
|
2,5
|
4.3975522
|
2.1684808
|
0.1084240
|
| 15
|
2,55
|
4.5284683
|
2.1644085
|
0.1082204
|
| 16
|
2,6
|
4.6607518
|
2.1610801
|
0.1080540
|
| 17
|
2,65
|
4.7944021
|
2.1587230
|
0.1079362
|
| 18
|
2,7
|
4.9294193
|
2.1575712
|
0.1078786
|
| 19
|
2,75
|
5.0658041
|
2.1578639
|
0.1078932
|
| 20
|
2,8
|
5.2035577
|
2.1598449
|
0.1079922
|
Поправка Ричардсона Ri
для метода Эйлера:

| -0.07065289342943
|
| -0.13216188575150
|
| -0.18444601911606
|
| -0.26010250688842
|
| -0.33631248297229
|
| -0.41398824090458
|
Поправка Ричардсона Ri
для метода Рунге-Кутта:

| -0.07315885784
|
| -0.15166859920
|
| -0.23543241393
|
| -0.32440371076
|
| -0.41858637980
|
| -0.51803478491
|
В ходе выполнения курсовой работы был проведен сравнительный анализ численных методов, таких как итерация, интерполяция, численное дифференцирование и интегрирование, а также метод Эйлера.
В настоящее время появилось значительное число различных программных продуктов (MathCAD, MathLAB и т.д.), с помощью которых, задавая только входные данные, можно решить значительное число задач.
Для более глубокого анализа численных методов мы использовали средства MathCAD, а также алгоритмические языки программирования.
1. Р.Ф. Хемминг "Численные методы (для научных работников и инженеров)". - Москва, 1972.
2. А.А. Амосов, А.Ю. Дубинский, Н.В. Копченова "Вычислительные методы для инженеров". - Москва, "Высшая школа", 1994.
3. Ф.В. Формалев, Д.Л. Ревизников "Численные методы". - М.: ФИЗМАТЛИТ, 2004.
4. Ю. Тарасевич "Численные методы на MathCAD’e". - Астраханский гос. пед. ун-т: Астрахань 2000.
|