ОКРЕМІ ВИПАДКИ ЗАДАЧ ОПТИМАЛЬНОГО СТОХАСТИЧНОГО КЕРУВАННЯ
1.Зовнішній інтеграл
Функції  і і  можуть бути довільними, а математичні сподівання можна обчислювати, якщо можуть бути довільними, а математичні сподівання можна обчислювати, якщо  як функція від як функція від  є вимірною. є вимірною.
Якщо ж оптимальна стратегія, отримана в результаті оптимізації, виявиться невимірною, то і функція  може виявитися невимірною. У цьому випадку математичне сподівання невизначено. може виявитися невимірною. У цьому випадку математичне сподівання невизначено.
Для розв’язання цієї проблеми застосовують два підходи. Перший полягає в накладенні на функції  і і  таких обмежень, які забезпечували б вимірність підінтегральної функції на кожному кроці оптимізації таких обмежень, які забезпечували б вимірність підінтегральної функції на кожному кроці оптимізації  : функції : функції  і і  , ,  , повинні бути неперервними по своїх аргументах і повинна існувати щільність імовірності розподілу випадкової величини , повинні бути неперервними по своїх аргументах і повинна існувати щільність імовірності розподілу випадкової величини  , а множини , а множини  значень припустимих стратегій повинні бути компактними. значень припустимих стратегій повинні бути компактними.
На жаль, на практиці ці вимоги не завжди виконуються. Тому другий підхід пов’язаний з використанням зовнішнього інтеграла.
Позначимо через  простір елементарних подій, що є довільною множиною, а простір елементарних подій, що є довільною множиною, а  – деяка система підмножин множини – деяка система підмножин множини  . .
Математичним сподіванням випадкової величини  , заданої на імовірнісному просторі , заданої на імовірнісному просторі  , називається число , називається число  , якщо інтеграл з правої частини існує. , якщо інтеграл з правої частини існує.
Нехай  і і  – борелівські простори, – борелівські простори,  , ,  є є  -алгеброю в -алгеброю в  . Функція . Функція  називається називається  -вимірною, якщо -вимірною, якщо  для будь-якої множини для будь-якої множини  . Тут . Тут  – борелівська – борелівська  -алгебра простору -алгебра простору  . .
Для функції  , ( , ( ) зовнішній інтеграл за мірою ) зовнішній інтеграл за мірою  визначається як нижня грань інтегралів від всіх вимірних функцій визначається як нижня грань інтегралів від всіх вимірних функцій  ( ( ), що мажорують ), що мажорують  , тобто , тобто
 , ,  . .
Тут  – функція розподілу випадкової величини – функція розподілу випадкової величини  , що відповідає ймовірнісній мірі , що відповідає ймовірнісній мірі  . .
Для довільної функції  має місце співвідношення: має місце співвідношення:
 , ,
де  , ,  , і вважають, що , і вважають, що  . .
Оскільки зовнішній інтеграл визначений для будь-якої функції, як для вимірної, так і для невимірної, то ніяких додаткових обмежень на функції  і і  накладати не треба. накладати не треба.
Для вимірних функцій обидва види математичних сподівань співпадають. Отже, у постановках задач можна замінити звичайне математичне сподівання на зовнішнє, і навіть якщо знайдена при цьому функція  виявиться вимірною, то отримана стратегія керування не перестане бути оптимальною. виявиться вимірною, то отримана стратегія керування не перестане бути оптимальною.
Зовнішня міра множини  визначається співвідношенням визначається співвідношенням  . .
Для будь-якої множини 
 , ,
де  – це індикатор множини – це індикатор множини  , що визначається як , що визначається як 
а) якщо  , то , то  ; ;
б) якщо  і і  , то , то  ; ;
в) якщо  або або  , то , то  ; ;
г) якщо  задовольняє рівності задовольняє рівності  , то для будь-якої функції , то для будь-якої функції  має місце рівність має місце рівність  ; ;
д) якщо  , то , то  для будь-якої функції для будь-якої функції  ; ;
е) якщо  і і  , то , то  . Якщо при цьому хоча б одна з функцій . Якщо при цьому хоча б одна з функцій  або або   -вимірна, то останнє співвідношення вірно зі знаком рівності. -вимірна, то останнє співвідношення вірно зі знаком рівності.
Позначимо через  дійсну пряму, а через дійсну пряму, а через  – розширену дійсну пряму і надалі у всіх висновках замість дійсної прямої використовуватимемо поняття розширеної дійсної прямої. – розширену дійсну пряму і надалі у всіх висновках замість дійсної прямої використовуватимемо поняття розширеної дійсної прямої.
Вважатимемо, що для розширеної дійсної прямої мають місце всі співвідношення порядку додавання і множення, які було введено для  , і припустимо, що , і припустимо, що  і і  . .
Позначимо через  множину всіх дійсних у розширеному розумінні функцій множину всіх дійсних у розширеному розумінні функцій  , де , де  – простір станів. – простір станів.
 – банахів простір всіх обмежених дійсних функцій – банахів простір всіх обмежених дійсних функцій  з нормою, що визначається за формулою з нормою, що визначається за формулою
 , ,  . .
Позначатимемо  , якщо , якщо  , ,  , ,  і і  , якщо , якщо  , ,  , ,  . .
Для будь-якої функції  і будь-якого числа і будь-якого числа  позначимо через позначимо через  функцію, що приймає значення функцію, що приймає значення  в кожній точці в кожній точці  , так, що , так, що
 , ,  . .
Припущення монотонності. Для будь-яких станів  , керування , керування  і функцій і функцій  мають місце нерівності мають місце нерівності
 якщо якщо  і і  ; ;
 , якщо , якщо  і і  ; ;
 , якщо , якщо  , ,  і і  . .
Для будь-якого  стратегія стратегія  називається називається  -оптимальною при горизонті -оптимальною при горизонті  , якщо , якщо

і  -оптимальною, якщо -оптимальною, якщо

Багато задач послідовної оптимізації, що становлять практичний інтерес, можуть розглядатися як окремі випадки задач загального виду. Розглянемо деякі з них:
· задачі детермінованого оптимального керування;
· задачі стохастичного керування зі зліченним простором збурень;
· задачі стохастичного керування із зовнішнім інтегралом;
· задачі стохастичного керування з мультиплікативним функціоналом витрат;
· задачі мінімаксного стохастичного керування.
2. Детерміноване оптимальне керування
Розглянемо відображення  , що задане формулою , що задане формулою
 , ,  , ,  , ,  (1) (1)
за таких припущень:
функції  і і  відображають множину відображають множину  відповідно в множини відповідно в множини  і і  , тобто , тобто  , ,  ; скаляр ; скаляр  додатний. додатний.
За цих умов відображення  задовольняє припущенню монотонності. Якщо функція задовольняє припущенню монотонності. Якщо функція  дорівнює нулю, тобто дорівнює нулю, тобто  , ,  , то відповідна , то відповідна  -крокова задача оптимізації (1) набуває вигляду: -крокова задача оптимізації (1) набуває вигляду:
 , (2) , (2)
 . (3) . (3)
Ця задача є задачею детермінованого оптимального керування зі скінченним горизонтом. Задача з нескінченним горизонтом має наступний вигляд:
 , (4) , (4)
 . (5) . (5)
Границя в (4) існує, якщо має місце хоча б одна з наступних умов:
·  , ,  , ,  ; ;
·  , ,  , ,  ; ;
·  , ,  , ,  , ,  і деякого і деякого  . .
У задачі (4) – (5) може бути уведене додаткове обмеження на стан системи  , ,  . У такому разі, якщо . У такому разі, якщо  , позначатимемо , позначатимемо  . .
3. Оптимальне стохастичне керування: зліченний простір збурень
Розглянемо відображення  , що задане формулою , що задане формулою
 , (6) , (6)
за таких припущень:
параметр  приймає значення зі зліченної множини приймає значення зі зліченної множини  з заданим розподілом ймовірностей з заданим розподілом ймовірностей  , що залежать від , що залежать від  і і  ; функції ; функції  і і  відображають множину відображають множину  відповідно в множини відповідно в множини  і і  , тобто , тобто  , ,  ; скаляр ; скаляр  додатний. додатний.
Якщо  , ,  , – елементи множини , – елементи множини  , ,  – довільний розподіл ймовірностей на – довільний розподіл ймовірностей на  , а , а  – деяка функція, то математичне сподівання визначається за формулою – деяка функція, то математичне сподівання визначається за формулою
 , ,
де  , ,
 , ,
 . .
Оскільки  , то математичне сподівання , то математичне сподівання  визначене для будь-якої функції визначене для будь-якої функції  і будь-якого розподілу ймовірностей і будь-якого розподілу ймовірностей  на множині на множині  . .
Зокрема, якщо  , ,  ,… – розподіл ймовірностей ,… – розподіл ймовірностей  на множині на множині  , то формулу (6) можна переписати так: , то формулу (6) можна переписати так:

При використанні цього співвідношення треба пам’ятати, що для двох функцій  , ,  рівність рівність  має місце, якщо виконується хоча б одна з трьох умов: має місце, якщо виконується хоча б одна з трьох умов:
 та та  ; ;
 та та  ; ;
 та та  . .
Відображення  задовольняє припущенню монотонності. Якщо функція задовольняє припущенню монотонності. Якщо функція  – тотожний нуль, тобто – тотожний нуль, тобто  , ,  , то за умови , то за умови  , ,  , функцію витрат за , функцію витрат за  кроків можна подати у вигляді: кроків можна подати у вигляді:
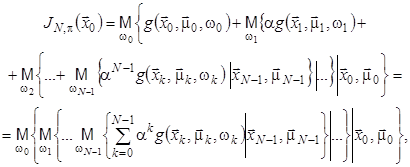 (7) (7)
де  , ,  . .
Ця умова означає, що математичне сподівання обчислюється послідовно по всіх випадкових величинах  . .
При цьому зміна порядку операцій додавання і узяття математичного сподівання припустима, тому що  , ,  , і для довільних простору з мірою , і для довільних простору з мірою  , вимірної функції , вимірної функції  і числа і числа  має місце рівність має місце рівність  . .
Якщо виконується одна з двох нерівностей
 або або
 , ,
то функцію витрат за  кроків кроків  можна записати у вигляді: можна записати у вигляді:
 , ,
де математичне сподівання обчислюється на добутку мір на  , а стани , а стани  , ,  , виражаються через , виражаються через  за допомогою рівняння за допомогою рівняння  . .
Якщо функція  допускає подання у такому вигляді для будь-якого початкового стану допускає подання у такому вигляді для будь-якого початкового стану  та будь-якої стратегії та будь-якої стратегії  , то , то  -крокова задача може бути сформульована так: -крокова задача може бути сформульована так:
 , (8) , (8)
 . (9) . (9)
Відповідна задача з нескінченним горизонтом формулюється так:
 , (10) , (10)
 . (11) . (11)
Границя в (10) існує при виконанні будь-якої з трьох наступних умов:
·  , ,  , ,  , ,  ; ;
·  , ,  , ,  , ,  ; ;
·  , ,  , ,  , ,  , ,  і деякого і деякого  . .
Математичне сподівання визначається і як звичайний інтеграл, і як зовнішній інтеграл з  -алгеброю в множині -алгеброю в множині  , що складається із всіх підмножин , що складається із всіх підмножин  , в залежності від вимірності або невимірності функцій. , в залежності від вимірності або невимірності функцій.
Для багатьох практичних задач виконується припущення про зліченність множини  . .
Якщо ж множина  незліченна, то справа ускладнюється необхідністю обчислення математичного сподівання незліченна, то справа ускладнюється необхідністю обчислення математичного сподівання

для будь-якої функції  . Подолання цих труднощів і пов’язане з використанням зовнішнього інтеграла. . Подолання цих труднощів і пов’язане з використанням зовнішнього інтеграла.
|