КУРСОВАЯ РАБОТА
на тему:
«Разработка сменного модуля для изучения резистивного
соединения типа «Треугольник»»
Содержание
Введение
1. Теоретическая часть
1.1 Основные понятия
1.2 Уравнения передачи четырехполюсников
1.3 Применение матриц к расчету четырехполюсников
1.4 Режимы четырехполюсников
1.5 Расчет четырехполюсников
2. Практическая часть
2.1 Проектирование модуля
2.2 Изготовление модуля
3. Расчетная часть
Лабораторная работа
Литература
Введение
Целью данной курсовой работы является проектирование и изготовление сменного модуля для проведения лабораторных работ по изучению резистивного соединения типа «треугольник».
На практике часто встречаются соединения элементов, которые нельзя свести только к последовательному или параллельному соединению. Примером подобного соединения являются соединения многолучевой звездой и многоугольником. Наиболее часто встречаются случаи трёхлучевой звезды и треугольника.
В данной работе соединение треугольником реализовано в симметричном П-образном четырехполюснике.
1. Теоретическая часть
1.1 Основные понятия
В технике связи под четырехполюсниками
понимают электрическую цепь (или ее часть) любой сложности, имеющую две пары зажимов для подключения к источнику и приемнику электрической энергии. Зажимы, к которым подключается источник, называются входными
, а зажимы, к которым присоединяется приемник (нагрузка), – выходными зажимами (полюсами).
В общем виде четырехполюсник изображают, как показано на рис. 1. Ко входу четырехполюсника 1–1’ подключен источник электрической энергии с задающим напряжением Uг
и внутренним сопротивлением Zг
. К выходным зажимам 2–2’ присоединена нагрузка с сопротивлением Zн
. На входных зажимах действует напряжение U1
; на выходных – U2
. Через входные зажимы протекает ток I1
, через выходные зажимы – I2
. Заметим, что в роли источника и приемника электрической энергии могут выступать другие четырехполюсники.
Рис. 1.
Различают четырехполюсники линейные
и нелинейные
. Линейные четырехполюсники отличаются от нелинейных тем, что не содержат нелинейных элементов (НЭ) и поэтому характеризуются линейной зависимостью напряжения и тока на выходных зажимах от напряжения и тока на входных зажимах. Примерами линейных четырехполюсников являются электрические фильтры, линия связи, трансформатор без сердечника
; примерами нелинейных – преобразователь частоты (содержащий диоды) в радиоприемнике, выпрямитель переменного тока, трансформатор со стальным сердечником (при работе с насыщением стали)
.
Четырехполюсники бывают пассивными
и активными
. Пассивные схемы не содержат источников электрической энергии, активные – содержат. Последние могут содержать зависимые и независимые источники. Примером активного четырехполюсника с зависимыми источниками может служить любой усилитель; примером пассивного – LC-фильтр.
В зависимости от структуры различают четырехполюсники мостовые
(рис. 2) и лестничные
: Г-образные (рис. 3), Т-образные (рис. 4), П-образные (рис. 5). Промежуточное положение занимают Т – образно-мостовые
(Т – перекрытые) схемы четырехполюсников (рис. 6).
Рис. 2 Рис. 3
Рис. 4 Рис. 5

Рис. 6
Четырехполюсники делятся на симметричные
и несимметричные
. В симметричном четырехполюснике перемена местами входных зажимов не изменяет напряжений и токов в цепи, с которой он соединен. Четырехполюсники, кроме электрической симметрии, могут иметь структурную симметрию, определяемую относительно вертикальной оси симметрии. Так, Т – образный, П – образный и Т – перекрытый четырехполюсники имеют вертикальную ось симметрии при Z1
=Z3
. Мостовая схема структурно симметрична. Очевидно, четырехполюсники, симметричные в структурном отношении, обладают электрической симметрией.
Четырехполюсники могут быть уравновешенными
и неуравновешенными
. Уравновешенные четырехполюсники имеют горизонтальную ось симметрии (например, мостовая схема на рис. 2) и используется, когда необходимо сделать зажимы симметричными относительно какой-либо точки (например – земли). Можно сделать уравновешенной любую из лестничных схем четырехполюсников.
Четырехполюсники также делятся на обратимые
и необратимые
. Обратимые четырехполюсники позволяют передавать энергию в обоих направлениях; для них справедлива теорема обратимости или взаимности, в соответствии с которой отношение напряжения на входе к току не меняется при перемене местами зажимов.
1.2 Уравнения передачи четырехполюсников
Основной задачей теории четырехполюсников является установление соотношений между четырьмя величинами: напряжениями на входе и выходе, а также токами, протекающими через входные и выходные зажимы. Уравнения, дающие зависимость между U1
, U2
, I1
, и I2
, называются уравнениями передачи четырехполюсника
. Для линейных четырехполюсников эти уравнения будут линейными. Величины, связывающие в уравнениях передачи напряжения и токи, называются параметрами четырехполюсника
.
Сложная электрическая цепь, имеющая входные и выходные зажимы, может рассматриваться как совокупность четырехполюсников, соединенных по определенной схеме. Зная параметры этих четырехполюсников, можно вычислить параметры сложного четырехполюсника и получить тем самым зависимость между напряжениями и токами на зажимах результирующего сложного четырехполюсника, не производя расчетов всех напряжений и токов внутри заданной схемы.
Кроме того, теория четырехполюсников позволяет решить обратную задачу: по заданным напряжениям и токам найти параметры четырехполюсника и затем построить его схему и рассчитать элементы, т.е. решить задачу синтеза.
Например, если к вторичным выводам четырехполюсника подключен приемник с сопротивлением нагрузки Zн
, а к первичным – источник ЭДС Е1
(рис. 1), то при заданном напряжении на выводах приемника U2
и токе I2
=U2
/Z2
можно определить необходимое напряжение источника питания на первичных выводах U1
=E1
и ток источника I1
по уравнению:
 U1
=A11
U2
+A12
I2 U1
=A11
U2
+A12
I2
I1
=A21
U2
+A22
I2
(1)
Коэффициенты, входящие в систему уравнений, связывающую входные U1
и I1
и выходные U2
и I2
напряжения и токи называются А-параметрами
, или обобщенными параметрами
. Уравнения называются уравнениями передачи
в А-параметрах
. Параметры А11
и А22
являются безразмерными, параметр А12
имеет размерность сопротивления; параметр А21
– размерность проводимости.
Свойства параметров-коэффициентов
Параметры, образованные из коэффициентов уравнений передачи, объединяют одним названием параметры-коэффициенты
.
Свойства:
1. Параметры-коэффициенты определяются только схемой четырехполюсника и ее элементами и не зависят от внешних цепей, между которыми может быть включен четырехполюсник, т.е. они характеризуют собственно четырехполюсник.
2. Все системы параметров-коэффициентов описывают один и тот же четырехполюсник, поэтому между различными системами параметров-коэффициентов существует однозначная взаимосвязь.
3. Пассивный четырехполюсник полностью характеризуется не более чем тремя независимыми параметрами.
4. При изменении направления передачи энергии через четырехполюсник во всех выражениях, включающих А – параметры, коэффициенты А11
и А22
меняются местами.
5. Симметричные пассивные четырехполюсники имеют только два независимых параметра. В самом деле, в случае симметричного пассивного четырехполюсника не имеет значения направление передачи энергии: напряжения и токи на входе и выходе не изменяются при замене местами зажимов.
6. Параметры-коэффициенты имеют определенный физический смысл. Для выявления этого физического смысла следует четырехполюсник поставить в такой режим работы, при котором уравнения передачи содержат лишь один интересующий нас параметр. Подобное произойдет, если использовать режимы холостого хода и короткого замыкания.
7. Из предыдущего свойства следует, что параметры-коэффициенты являются комплексными величинами, так как они определяются отношением комплексных амплитуд (действующих значений) напряжений и токов. В случае анализа четырехполюсника в режиме негармонических колебаний используют спектральные представления электрических величин. Можно показать, что параметры-коэффициенты, рассматриваемые относительно не отдельной частоты, а определенного спектра частот, являются рациональными функциями оператора jω. При переходе от оператора jω к оператору p
параметры-коэффициенты представляют собой рациональные функции оператора p
.
1.3 Применение матриц к расчету четырехполюсников
Любую из систем уравнений передачи четырехполюсника можно записать в матричной форме. В частности для системы уравнений в А – параметрах.
 U1
=A11
U2
+A12
I2 U1
=A11
U2
+A12
I2
I1
=A21
U2
+A22
I2
получим:
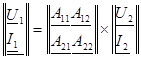 (2) (2)
где   – квадратная матрица коэффициентов; – квадратная матрица коэффициентов;
 и и  – матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах. – матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах.
Всего можно записать шесть различных по форме, но по существу эквивалентных, т.е. математически равносильных, пар уравнений (число сочетаний из четырех по два).
1.4 Режимы четырехполюсников
При расчете режима работы четырехполюсника с применением различных типов уравнений принято выбирать положительные направления токов неодинаковыми. Положительные направления токов по рис. 1 (I1
и I2
) часто выбирают для пассивных четырехполюсников с источником питания на первичных – входных выводах и приемником с сопротивлением Zн
на вторичных выходных выводах и записи уравнений типа А.
Входное сопротивление четырехполюсника
Если к одной паре зажимов четырехполюсника, например 2–2’, подключить произвольное сопротивление Zн
(рис. 7), то со стороны другой пары зажимов, т.е. 1–1’, четырехполюсник можно рассматривать как двухполюсник с входным сопротивлением Zвх1
, которое называют входным сопротивлением четырехполюсника.
Следовательно,
Zвх1
=U1
/I1
. (7)
Рис. 7
Рис. 8
Входное сопротивление можно выразить через параметры четырехполюсника. Проще всего это сделать, воспользовавшись выражениями для U1
и I1
из уравнений передачи в А – параметрах. В этом случае
 (8) (8)
так как
U2
=Z2
I2
На рис. 8 Показан тот же четырехполюсник, нагруженный со стороны зажимов 1–1’ на сопротивление Zг
. Его входное сопротивление со стороны зажимов 2–2’ равно Zвх2
=U’1
/I’1
. (9)
В связи с тем, что изменилось направление передачи энергии, следует воспользоваться уравнениями передачи. Тогда
 (10) (10)
Так как
U’2
=ZГ
I’2
. (11)
Заметим что при изменении направления передачи энергии через четырехполюсник в выражениях (8) и (10) параметры А11
и А22
поменялись местами.
Входное сопротивление четырехполюсника не является его внутренним параметром, так как оно зависит не только от свойств четырехполюсника, но и от свойств внешней цепи (нагрузки), на которую замкнута пара зажимов четырехполюсника.
1.5 Расчеты четырехполюсников
Рассмотрим симметричный четырехполюсник. При питании четырехполюсника со стороны первичных выводов и разомкнутых вторичных получаем Z1х
=Z11
. При питании со стороны вторичных выводов и разомкнутых первичных у симметричного четырехполюсника должно быть такое же входное сопротивление Z2х
=Z1х.
Из уравнений
U1
=Z11
I1
+Z12
I2
U2
=Z21
I1
+Z22
I2
или

при I1
=0 получаем Z22
=U2
/I2
=Zвх
, и, следовательно, Z22
=Z11
.
Такие же рассуждения приводят к равенствам
A11
=A22
; Y11
=Y22
.
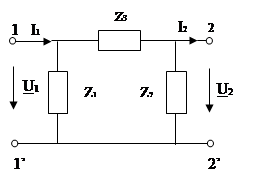
Рис. 9
Найдем коэффициенты уравнений типа А симметричного П – образного четырехполюсника (рис. 9).
При холостом ходе на вторичных выводах (I'2
=0) из рис. 9 следует, что
I1X
=U1
/(Z1
/2+Z2
)
U2X
=Z2
I1X
(12)
Или
U2
X
=U1
Z2
/(Z1
/2+Z2
). (13)
Сравнив эти выражения с уравнениями при I2
’=0, определим
A21
=1/Z2
A11
=1+Z1
/2Z2
. (14)
При коротком замыкании вторичных выводов (U2
=0) из рис. 9 следует, что I2
K
’=I1
K
Z2
/(Z2
+Z1
/2) или
I1
K
=(1+Z1
/2Z2
) I2
K
’;
 . (15) . (15)
Сравнив эти выражения с уравнениями при U2
=0, найдем
A12
=Z1
(1+Z1
/4Z2
),
A22
=(1+Z1
/2Z2
), (16)
т.е. A22
=A11
, как и должно быть у симметричного четырехполюсника.
Экспериментальное определение коэффициентов и входных сопротивлений
Первичные параметры каждого данного четырехполюсника могут быть определены экспериментально при измерении режима (напряжений и токов) на первичных и вторичных выводах. Например, при питании четырехполюсника со стороны первичных выводов (напряжение U1
) и холостом ходе на вторичных (напряжение Uвх
, токи I1
=I1Х
, I2
’=I2Х
’=0) находим:
A11
=U1
/U2
X
A21
=I1
X
/U2
X
, (17)
а при коротком замыкании вторичных выводов (напряжение U2
=U2
K
=0, токи I1
=I1
K
, I2
’=I2
K
’),
A12
=U1
/I2K
’
A22
=I1K
/I2K
’. (18)
При работе четырехполюсника в цепи постоянного тока для вычисления коэффициентов достаточно измерить напряжения и токи.
Сопротивления холостого хода и короткого замыкания могут быть измерены теми же методами, что и любые другие сопротивления, например при помощи измерительного моста или амперметра, вольтметра, включенных только со стороны первичных или только со стороны вторичных выводов.
2 Практическая часть
2.1 Проектирование модуля
1. Проектируется схема для исследования соединения.
2. Подбираются радиодетали, которые будут располагаться на будущей печатной плате модуля. Определяется подключение к исследуемой схеме измерительных приборов, источника сигнала.
3. Разрабатывается печатная плата.
2.2 Изготовление модуля
1. После разработки печатной платы, она выпиливается из текстолита.
2. На стороне, покрытой слоем металла, лаком наносятся дорожки. После этого плата вытравливается в растворе хлористого железа, лак удаляется, и дорожки покрываются оловом. В текстолите для последующей впайки радиодеталей сверлятся отверстия.
3. На плату, в соответствии со схемой, монтируются резисторы, припаиваются провода.
4. Плата помещается в корпус модуля. В соответствии со схемой, провода припаиваются к тумблерам, плате, разъему.
5. Проверяется работоспособность модуля.
Номиналы резистивных элементов:
R1
= 3 кОм,
R2
= 10 кОм,
R3
= 3 кОм.
К входным выводам 1–1’ подключен источник питания, к выходным 2–2’ – нагрузка. Вольтметр V1
имеет возможность переключения с помощью тумблера S1
со входа схемы на выход и обратно.
Тумблеры S2
(S2.1
и S2.2
)и S3
(S3.1
и S3.2
) переключают амперметр с измерения тока на входе схемы на измерение тока на выходе и обратно.
Итоговая схема:
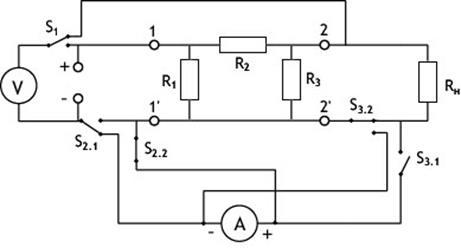
Рис. 14
3. Расчетная часть
Разработан сменный модуль по соединению «треугольник» для установки «Каскад». Сменный модуль соединяется с установкой «Каскад», получаем схему цепи, показанную на рисунке 15.
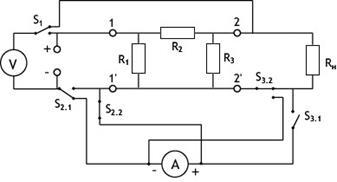
Рис. 15
Сопротивление резистивных элементов:
R1
= R3
= 3 кОм,
R2
= 10 кОм.
После проведения лабораторных измерений получили:
напряжение на входе
U1
=;
напряжение на выходе
U2
=;
ток на входе
I1
=;
ток на выходе
I2
=.
Найдем А-параметры для данного четырехполюсника из уравнений (17), (18):
A11
=U1
/U2X
А11
=
А11
=
A21
=I1X
/U2X
А21
=
А21
=
A12
=U1
/I2K
’
А12
=
А12
=
A22
=I1K
/I2K
’
А22
=
А22
=
Сделаем проверку по формулам (14), (16).
A12
=Z1
(1+Z1
/4Z2
),
A12
=
A12
=
A22
=(1+Z1
/2Z2
)
A22
=
A22
=
A21
=1/Z2
A21
=
A21
=
A11
=1+Z1
/2Z2
.
A11
=
A11
=
Вычисления по формулам (14), (16) отличается от результатов, полученных по формулам (17), (18) на величину погрешности измерений.
Расчет погрешностей:
∆U=0,01 B
∆I=0,01 mA
∆ A =
∆ A =
∆ A =
∆ A =
∆ A =
∆ A =
∆ A =
∆ A =
∆ A =
∆ A=
∆ A=
∆ A=
Лабораторная работа
Исследование соединения типа «Треугольник»
Приборы и оборудование:
блок питания, сменный модуль, измерительные приборы.
Методические указания
В технике связи под четырехполюсниками понимают электрическую цепь (или ее часть) любой сложности, имеющую две пары зажимов для подключения к источнику и приемнику электрической энергии.
В общем виде четырехполюсник изображают, как показано на рис. 1. Ко входу четырехполюсника 1–1’ подключен источник электрической энергии с задающим напряжением Uг
и внутренним сопротивлением Zг
. К выходным зажимам 2–2’ присоединена нагрузка с сопротивлением Zн
. На входных зажимах действует напряжение U1
; на выходных – U2
. Через входные зажимы протекает ток I1
, через выходные зажимы – I2
. Заметим, что в роли источника и приемника электрической энергии могут выступать другие четырехполюсники.
Рис. 1.
Системы уравнений четырехполюсника
Основной задачей теории четырехполюсников является установление соотношений между четырьмя величинами: напряжениями на входе и выходе, а также токами, протекающими через входные и выходные зажимы. Уравнения, дающие зависимость между U1
, U2
, I1
, и I2
, называются уравнениями передачи четырехполюсника. Для линейных четырехполюсников эти уравнения будут линейными. Величины, связывающие в уравнениях передачи напряжения и токи, называются параметрами четырехполюсника.
Например, если к вторичным выводам четырехполюсника подключен приемник с сопротивлением нагрузки Zн
, а к первичным – источник ЭДС Е1
(рис. 1), то при заданном напряжении на выводах приемника U2
и токе I2
=U2
/Z2
можно определить необходимое напряжение источника питания на первичных выводах U1
=E1
и ток источника I1
по уравнению:
 U1
=A11
U2
+A12
I2 U1
=A11
U2
+A12
I2
I1
=A21
U2
+A22
I2
(1)
Коэффициенты, входящие в систему уравнений, связывающую входные U1
и I1
и выходные U2
и I2
напряжения и токи называются А-параметрами, или обобщенными параметрами. Уравнения называются уравнениями передачи в А-параметрах. Параметры А11
и А22
являются безразмерными, параметр А12
имеет размерность сопротивления; параметр А21
– размерность проводимости.
Любую из систем уравнений передачи четырехполюсника можно записать в матричной форме. В частности для системы уравнений в А – параметрах.
 U1
=A11
U2
+A12
I2 U1
=A11
U2
+A12
I2
I1
=A21
U2
+A22
I2
(2)
получим:
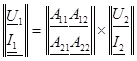 (3) (3)
где  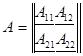 – квадратная матрица коэффициентов; – квадратная матрица коэффициентов;
 и и  – матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах. – матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах.
При расчете режима работы четырехполюсника с применением различных типов уравнений принято выбирать положительные направления токов неодинаковым. Положительные направления токов по рис. 1 (I1
и I2
) часто выбирают для пассивных четырехполюсников с источником питания на первичных – входных выводах и приемником с сопротивлением Zн
на вторичных выходных выводах и записи уравнений типа А.
Входное сопротивление четырехполюсника
Если к одной паре зажимов четырехполюсника, например 2–2’, подключить произвольное сопротивление Zн
(рис. 2), то со стороны другой пары зажимов, т.е. 1–1’, четырехполюсник можно рассматривать как двухполюсник с входным сопротивлением Zвх1
, которое называют входным сопротивлением четырехполюсника. Следовательно,
Zвх1
=U1
/I1
. (4)
Рис. 2

Рис. 3
Входное сопротивление можно выразить через параметры четырехполюсника. Проще всего это сделать, воспользовавшись выражениями для U1
и I1
из уравнений передачи в А – параметрах. В этом случае
 (5) (5)
так как
U2
=Z2
I2
(6)
На рис. 3 Показан тот же четырехполюсник, нагруженный со стороны зажимов 1–1’ на сопротивление Zг
. Его входное сопротивление со стороны зажимов 2–2’ равно
Zвх2
=U’1
/I’1
. (7)
В связи с тем, что изменилось направление передачи энергии, следует воспользоваться уравнениями передачи. Тогда
 (8) (8)
Так как
U’2
=ZГ
I’2
. (9)
Заметим что при изменении направления передачи энергии через четырехполюсник в выражениях (5) и (8) параметры А11
и А22
поменялись местами.
Входное сопротивление четырехполюсника не является его внутренним параметром, так как оно зависит не только от свойств четырехполюсника, но и от свойств внешней цепи (нагрузки), на которую замкнута пара зажимов четырехполюсника.
Рассмотрим симметричный четырехполюсник. При питании четырехполюсника со стороны первичных выводов и разомкнутых вторичных получаем Z1х
=Z11
. При питании со стороны вторичных выводов и разомкнутых первичных у симметричного четырехполюсника должно быть такое же входное сопротивление Z2х
=Z1х.
Из уравнений
U1
=Z11
Z1
+Z12
I2
U2
=Z21
I1
+Z22
I2
или

при I1
=0 получаем Z22
=U2
/I2
=Zвх
, и, следовательно, Z22
=Z11
.
Такие же рассуждения приводят к равенствам
A11
=A22
; Y11
=Y22
.
Рис. 4
Найдем коэффициенты уравнений типа А симметричного П – образного четырехполюсника (рис. 4).
При холостом ходе на вторичных выводах (I'2
=0) из рис. 4 следует, что
I1X
=U1
/(Z1
/2+Z2
)
U2X
=Z2
I1X
(10)
Или
U2
X
=U1
Z2
/(Z1
/2+Z2
). (11)
Сравнив эти выражения с уравнениями при I2
’=0, определим
A21
=1/Z2
A11
=1+Z1
/2Z2
. (12)
При коротком замыкании вторичных выводов (U2
=0) из рис. 4 следует, что I2
K
’=I1
K
Z2
/(Z2
+Z1
/2) или I1
K
=(1+Z1
/2Z2
) I2
K
’;
 . (13) . (13)
Сравнив эти выражения с уравнениями при U2
=0, найдем
A12
=Z1
(1+Z1
/4Z2
),
A22
=(1+Z1
/2Z2
), т.е. A22
=A11
, как и должно быть у симметричного четырехполюсника.
Экспериментальное определение коэффициентов и входных сопротивлений
Первичные параметры каждого данного четырехполюсника могут быть определены экспериментально при измерении режима (напряжений и токов) на первичных и вторичных выводах. Например, при питании четырехполюсника со стороны первичных выводов (напряжение U1
) и холостом ходе на вторичных (напряжение Uвх
, токи I1
=I1Х
, I2
’=I2Х
’=0) находим:
A11
=U1
/U2
X
A21
=I1
X
/U2
X
(14)
а при коротком замыкании вторичных выводов (напряжение U2
=U2
K
=0, токи I1
=I1
K
, I2
’=I2
K
’),
A12
=U1
/I2K
’
A22
=I1K
/I2K
’. (15)
При работе четырехполюсника в цепи постоянного тока для вычисления коэффициентов достаточно измерить напряжения и токи.
Сопротивления холостого хода и короткого замыкания могут быть измерены теми же методами, что и любые другие сопротивления, например при помощи измерительного моста или амперметра, вольтметра, включенных только со стороны первичных или только со стороны вторичных выводов.
Список литературы
1. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. – М.: Радио и связь, 2000.
2. Зевеке Г.В., Ионкин П.А. Основы теории цепей. М.: ЭнергоАтомИздат, 1989.
3. Дмитриева В.Ф., Прокофьев В.Л. Основы физики – М.: Высшая школа, 2003.
|