302
Два положительных точечных заряда  и  закреплены на расстоянии  друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещение зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
 
Решение:
Определим знак заряда, при котором равновесие будет устойчивым.
Если заряд отрицательный, то при смещении его влево сила  (направленная влево) возрастает, а сила  (направленная вправо) возрастает. Под действием этой силы заряд удаляется от положения равновесия. То же происходит и при смещении заряда вправо. Равновесие будет неустойчивым.
Если заряд  положителен, то при смещении его влево сила (направленная вправо) возрастает, а сила (направленная влево) убывает, следовательно, результирующая сила будет направлена вправо и заряд возвращается к положению равновесия. То же происходит и при смещении заряда вправо. Равновесие будет устойчивым.
Предположим, что заряд находится в точке  . Тогда условие равновесия заряда запишется так:
Подставив в уравнение вместо сил их значения по закону Кулона, и произведя сокращения, получим:
Решая относительно  , получаем:
Так как  –эта точка расположена вне отрезка  , что невозможно для равновесия заряда .
Произведем вычисления: 
Ответ:
 положительный.
322
На двух концентрических сферах радиусом  и  равномерно распределены заряды с поверхностными плотностями  и  соответственно. Используя теорему Гаусса, найти зависимость  напряженности электрического поля от расстояния для трех областей:  и  . Принять  ,  . 2) вычислить напряженность  в точке, удаленной от центра на расстояние  и указать направление вектора  для значений  ,  . 3) построить график .
 
Решение:
1) Для определения напряженности  в области  проведем гауссову поверхность радиусом  .
По теореме Остроградского –Гаусса имеем:
Для области :  -заряда внутри сферы нет
Напряженность поля в области равна нулю.
Для области  проведем гауссову поверхность радиуса  :
Площадь гауссовой поверхности: 
Площадь поверхности шара: 
Для области  проведем гауссову поверхность радиуса  . Гауссова поверхность охватывает обе сферы:
2) Найдем напряженность для точки, удаленной от центра на расстояние  :
3) Строим график :
3) Строим график Е(r):
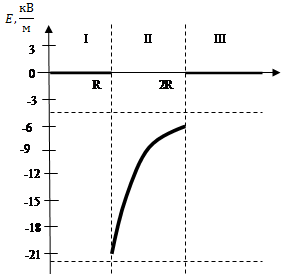
332
Электрическое поле создано зарядами  и  , находящимися в точках  и  соответственно ( ). Точка находится на прямой  ( ). Точка  находится на продолжении отрезка ( ). Определить работу сил поля, совершаемую при перемещении заряда  из точки в точку .
 
Решение:
Для определения работы А12
сил поля воспользуемся соотношением: 
Расстояние между точкой, в которой расположен заряд  и точкой по теореме Пифагора равно 
Применяя принцип суперпозиции электрических полей, определим потенциалы  и  точек и поля:
Разность потенциалов:
Искомая работа:
Проверим единицы измерения:
Произведем вычисления:
Ответ:
 .
352
Конденсаторы емкостями  ,  и  соединены последовательно и находятся под напряжением  . Определить напряжение и заряд на каждом из конденсаторов.
 
Решение:
Так как конденсаторы соединены последовательно, то:
Заряд:
Произведем вычисления:
Разности потенциалов:
Ответ:
 .
402
По двум скрещенным под прямым углом бесконечно длинным проводам текут токи и  ( ). Определить магнитную индукцию  в центре отрезка, перпендикулярного к обоим проводам, если длина его составляет  . Указать направление вектора для выбранных направлений тока.
 
Решение:
В соответствии с принципом суперпозиции магнитных полей, магнитная индукция  , создаваемая токами  и  определяется выражениями: 
Направление векторов и  найдем по правилу буравчика. Вектор , создаваемый 2-м проводом направлен перпендикулярно плоскости рисунка «от нас». Вектор , создаваемый 1-м проводом, направлен вверх от точки . Так как  , скалярно получаем: 
Магнитные индукции, создаваемые проводами определим по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током:
В нашем случае:  ; 
Получаем:
Искомая магнитная индукция:
Произведем вычисления:
Ответ:
412
Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи  . Определить силу  , действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном ее длине.
 
Решение:
Сила, действующая на провод с током в магнитном поле:
где  -угол между направлением тока в проводе и вектором магнитной индукции .
На стороны рамки, расположенные перпендикулярно проводу, действуют силы равные по модулю и противоположные по направлению, которые уравновешивают друг друга.
Магнитная индукция поля прямого тока:
Сила, действующая на ближайшую сторону рамки:
Сила, действующая на дальнюю сторону рамки:
Суммарная сила:
Проверим единицы измерения:
Произведем вычисления:
Ответ:
 .
442
Альфа-частица влетела в скрещенные под прямым углом магнитное ( ) и электрическое  поля. Определить ускорение  альфа-частицы в начальный момент времени, если ее скорость  перпендикулярна векторам и , причем силы, действующие со стороны этих полей, противоположно направлены.
 
Решение:
На движущуюся заряженную частицу в скрещенных магнитном и электрическом полях действуют две силы:
Сила Лоренца, направленная перпендикулярно скорости  и вектору магнитной индукции и кулоновская сила  , противоположно направленная вектору напряженности электростатического поля.
Ускорение можно найти по 2-му закону Ньютона:
Куловская сила: 
Сила Лоренца: 
Искомое ускорение электрона:
 -масса альфа-частицы
 - заряд -частицы
Проверим единицы измерения:
Произведем вычисления:
Ответ:
 .
462
В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. При этом по цепи прошел заряд  . Определить изменение магнитного потока  через кольцо; если сопротивление цепи гальванометра  .
 
Решение:
В тот момент, когда вставили магнит, произошло изменение магнитного поля. В кольце возникнет ЭДС индукции, определяемая основным законом электромагнитной индукции:
Возникшая ЭДС индукции вызовет в рамке индукционный ток, мгновенное значение которого можно определить, воспользовавшись законом Ома для полной цепи:
где –сопротивление гальванометра
Проинтегрируем последнее равенство:
Откуда искомая величина:
Проверим единицы измерения:
Произведем вычисления:
Ответ:
 .
Литература
1. Трофимова Т.И. Курс физики. М. 2000
2. Савельев И.В. Курс общей физики, в 5 т. М. 2001
3. Чертов А.Г., Воробьев А.А. Задачник по физике. М., 1981
|
