КОНТРОЛЬНАЯ РАБОТА №1 ПО ПРЕДМЕТУ «ГЕОДЕЗИЯ»
ВАРИАНТ
ШИФР Я(10) 56
Задание1 Ответы на вопросы «Основные сведения по геодезии»
I.
Сведения о фигуре Земли. Применяемые в геодезии системы координат. Ориентирование линий.
Вопрос: Что называют географическим или истинным азимутом и дирекционным углом? Какова зависимость между прямым и обратным дирекционными углами данной линии?
Ориентировать линию местности — значит найти ее направление относительно меридиана. В качестве углов, определяющих направление линий, служат азимуты, дирекционные углы и румбы.
Азимутом А называется горизонтальный угол, отсчитанный по ходу часовой стрелки от северной части меридиана до заданного направления от 0 до 360° (рис.1).Если азимут отсчитывается по ходу часовой стрелки от северного направления истинного меридиана до заданного направления от 0 до 360°, то такой азимут называется истинным, или географическим

Рис 1
Прямой азимут направления P1
P2
(см. рис.1.) будет A1
, а обратный для того же направления - А2
. Меридианы не параллельны между собой, поэтому азимут линии в каждой ее точке имеет разное значение. Угол между направлениями двух меридианов в данных двух точках называется сближением меридианов и обозначается через γ Как видно из рис 1, зависимость между прямым и обратным азимутами линии выражается формулой
А2
= А1
+180Ο
+ γ ;
А2=А1+/- 180 °
Азимуты в качестве ориентирных углов применимы на сфероидической или сферической поверхности Земли. При изображении земной поверхности на плоскости в какой-либо проекции, например Гаусса — Крюгера, пользуются плоскостным ориентирным углом, называемым дирекционным.


Δ
Рис. 2.
Дирекционным углом линии на плоскости называется угол между изображениями на ней осевого меридиана и заданным направлением по ходу часовой стрелки от 0 до 360°. Дирекционные углы обозначаются буквой α.
Как следует из рис.2, связь между азимутами и дирекционными углами выражается формулой
А = α + γ,
где γ— сближение меридианов в точке Р1
, т. е. угол между изображениями осевого меридиана и меридиана данной точки. При пользовании формулой надо иметь в виду, что сближение меридианов точек, расположенных к востоку от осевого меридиана, имеет знак плюс, а к западу — знак минус. Прямой и обратный дирекционные углы одной и той же линии отличаются на 180° и определяются:
αобр=αпр.+/-180гр.
Если обозначить разность долгот данного меридиана и осевого через I, то сближение меридианов будет связано с разностью долгот приближенной формулой
γ= IsinB,
где B - геодезическая широта данной точки.
I
I.
Общие сведения об измерениях и элементы математической обработки результатов геодезических измерений.
Вопрос: Что такое предельная погрешность и как её определяют?
Виды погрешностей измерений, их классификация измерения в геодезии рассматриваются с двух точек зрения: количественной и качественной, выражающей числовое значение измеренной величины, и качественной - характер её точность. Из практики известно, что даже при самой тщательной и аккуратной работе много кратные измерения не дают одинаковых результатов. Если обозначить истинное значение измеряемой величины X а результат измерения l от истинная ошибка измерения дельта определяется из выражения
Δ= l-X
Случайные погрешности характеризуют след свойствами. При определении условий измерения случайные не могут превышать известного предела, называемого предельной погрешностью. Это свойство позволяет обнаруживать и исключать из результатов измерений грубые ошибки. Положительные и отрицательные ошибки примерно одинаково часто встречаются в ряду измерений, что помогает выявлению систематических ошибок. Чем больше абсолютная величина ошибки, тем реже она встреч в ряде измерений. Среднее арифметическое из случайных ошибок измерений одной и той же величины, выполненных при один условиях, при неограниченном возрастании числа измерений стремится к 0. это свойство компенсации. Последнее свойство случайных ошибок позволяет установить принцип получения из ряда измерений одной и той же величины результата, наиболее близкого к её истинному значению т е. Наиболее точного. Таким результатом является среднее арифметическое из n измеренных значений данной величины. При бесконечно большом числе измерений n lim (l|n)=X точность окончательного результата тем выше чем больше n для правильного использования результатов измерений необходимо знать с какой точностью - с какой степенью близости к истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории ошибок служит предложенная Гауссом средняя квадратическая ошибка m, вычисленная по формуле где n число измерений данной величины. Эта формула применима для случаев, когда известно истинное значение измеряемой величины. Такие случаи в практике встречаются редко. В то же время из измерений можно получить результат, наиболее близкий к истинному значению - ариф середину. Средне квадрат ошибка подчитывается по ф Бесселя где - отклонения отдельных значений измеренной величины от ариф середины, называемую вероятнейшими ошибками. Точность ариф середины естественно будет выше точности отдельного измерения.
I
I
I . Линейные измерения
Вопрос: Каков принцип измерения расстояний нитяным дальномером? Напишите рабочую формулу.
Дальномерные определения расстояний
Идея оптических дальномеров основана на решении треугольника (прямоугольного или равнобедренного), в котором по малому (параллактическому) углу р и противолежащей ему стороне (базису) определяют расстояние D по формуле
D = bctgβ
Одна из величин (угол β или базис b) постоянна, другую измеряют. В соответствии с этим применяют дальномеры с постоянным углом и переменным базисом или с постоянным базисом и переменным углом.
Нитяной дальномер является дальномером с постоянным углом и переменным базисом, которым служит нивелирная рейка, вертикально устанавливаемая на конце отрезка, длину которого определяют. Дальномер состоит из двух горизонтальных нитей, параллельных средней горизонтальной нити сетки зрительной трубы геодезического инструмента (теодолит, нивелир,).Для измерения расстояния на одном конце отрезка устанавливают инструмент, на другом – нивелирную рейку.
Коэффициент дальномера обычно бывает равным 100, поэтому дальномерный отсчет по рейке в сантиметрах выразит искомое расстояние в метрах.Дальномерные нити сетки должны располагаться на равных расстояниях от средней горизонтальной нити, что проверяют по разности отсчетов по рейке по трем нитям: среднее из отсчетов по крайним нитям должно совпадать с отсчетом по средней нити (несовпадение отсчетов до 3 — 4 мм).
Независимо от паспортных данных инструмента следует определять коэффициент дальномера. Для этого на ровной местности выбирают линию длиной примерно 100 м, начало ее отмечают точкой, над которой центрируют инструмент. Далее в створе линии откладывают от начальной точки величину, постоянного слагаемого с (равную для труб с внутренней фокусировкой ,0,1 м) и от этой второй точки отмеряют расстояния, равные 20, 40, 60, 80 и 100 м. Затем определяют эти отложенные расстояния по дальномеру дважды, получая дальномерное расстояние как среднее значение из двух определений.
Сравнивая дальномерные расстояния с фактически отмеренными, вычисляют пять значений коэффициента К, а за окончательное значение принимают среднее арифметическое.
При значительном отклонении, значения К., от 100 целесообразно (для съемочных работ) к данному дальномеру изготовить свою рейку, для чего нужно установить загрунтованную рейку на отмеченном ранее, расстоянии 100 м, отметить на ней проекции дальномерных нитей и разделить полученный интервал (условный метр) на 100 равных частей. Такие же деления следует продолжить и на остальных частях загрунтованной рейки. Относительная погрешность определения расстояний нитяным дальномером составляет примерно 1:300 измеряемого расстояния.
Измеряя дальномером расстояние между двумя точками, получают длину отрезка, наклоненного к горизонту под некоторым углом, если угол наклона превышает 1°30', необходимо отсчитанное по дальномеру расстояние привести к горизонту.
Рабочая формула определения расстояния нитяным дальномером, будет следующая:

Где К- коэффициент дальномера, а с- постоянное слагаемое.
При измерении наклонных расстояний горизонтальное проложение определяют:

v
- угол наклона визирной оси зрительной трубы.
IV.Геодезические сети
Вопрос: В чем сущность прямой и обратной геодезической задач?
Прямая геодезическая задача
Для решения геодезических задач в строительстве наиболее целесообразной является система прямоугольных координат в проекции Гаусса—Крюгера. Для определения координат последующих точек при известных координатах начальной точки, известных расстояниях между точками и известных дирекционных углах сторон между точками решается прямая геодезическая задача.
Пусть имеем точку А с координатами XA
и YA
, а координаты точки В' обозначим через Х'B
и Y'B
(рис3). Проведем через точку A линию, параллельную оси абсцисс, а через точку В' — линию, параллельную оси ординат. В результате получим прямоугольный треугольник, катеты которого будут равны разностям координат:

AВ" = XB
. - XA
.
В'B"=YB
'-YA
'
или
ХВ
'– YА
= ± Δх
YВ'
– YА
= ± Δ y

Рис 4
Величины Δх и Δy называются приращениями координат.
Зная значения Δ х и Δy стороны АВ' и координаты
начальной точки А, можно определить координаты конечной точки В'
XB
'=XA
_±ΔX
YB
'=YA
± Δy
Иначе говоря, координата точки последующей равна координате точки предыдущей плюс соответствующее приращение, т. е. в общем случае:
Xn=Xn-1 +ΔX
Yn=Yn-1 +ΔY
В зависимости от направления стороны АВ' приращения координат Δх и Δ у могут иметь знак плюс или знак минус. Знаки приращений координат определяют по направлениям сторон, т. е по их дирекционным углам.
Из рис. видно, что: Δх=dcosαΔy = dsinα
Из рассмотрения (рис.4) следует, что приращения Δх и Δу координат есть не что иное, как ортогональные проекции горизонтального расстояния d между точками A и B' и другими на оси координат. Формулы являются формулами решения прямой геодезической задачи. Знаки приращений координат совпадают со знаками тригонометрических функций (соответственно синуса и косинуса дирекционного угла).
Приращения координат могут быть вычислены тремя способами: по таблицам натуральных значений тригонометрических функций; по таблицам логарифмов и по специальным таблицам для вычисления приращений координат, правила пользования, которыми изложены в объяснении к таблицам.
В практике геодезических работ для строительства приходится определять координаты не какой-либо одной точки, а ряда точек, связанных между собой горизонтальными приложениями между точками и дирекционными углами сторон, заключенных между этими точками.
Обратная геодезическая задача
В практике строительства весьма часто приходится определять длину стороны и ее дирекционный угол по известным координатам ее конечных точек, т. е. решать обратную геодезическую задачу. Такая задача возникает при проектировании и перенесении объектов строительства на местность.
Если известны координаты двух точек B' и А (см. рис4.), т. е. известны приращения координат по стороне АВ', то тангенс дирекционного угла стороны АВ' определяется из треугольника АВ"В':
tgα=Δy/Δx
Из формулы можно написать:
d=Δx/cosα d=Δy/sinα
D=√ (Xb'-Xa)2
+(Yb'-Ya)2
=√Δx2
+Δy2
При решении обратных геодезических задач пользуются пятизначными таблицами логарифмов. Для определения величины дирекционного угла четверть устанавливают по знакам приращений координат.
При наличии малых вычислительных машин и значительном количестве задач решение их рациональнее выполнять нелогарифмическим способом, пользуясь пятизначными таблицами натуральных значений тригонометрических функций.
Задание2 Решение задач
Задача 1 Определить дирекционные углы линий ВС и СД, если:
 ; ;
 

  =236гр 40,2мин.-189гр59,2мин=46гр41мин =236гр 40,2мин.-189гр59,2мин=46гр41мин
 =46гр41мин+180гр-159гр28,0мин=216гр41мин -159гр28,0мин=67гр13,0мин =46гр41мин+180гр-159гр28,0мин=216гр41мин -159гр28,0мин=67гр13,0мин
67гр13,0мин -10гр32,8мин=56гр40,2мин ( ) )
Задача 2 Определить прямоугольные координаты точки Д, если:
Х(В)=-14,02м
У(В)=627,98м
 =46гр41мин =46гр41мин
 =239,14м =239,14м
Х(С)=(-14,02м)+(cos46гр41мин х 239,14м)= (-14,02м)+( 239,14м х 0,68949)=150,865м
У(С)= 627,98м+(sin46гр41минмин х 239,14м)=627,98м+( 239,14м х 0,72429221172333114981112266078498)= 753,433м
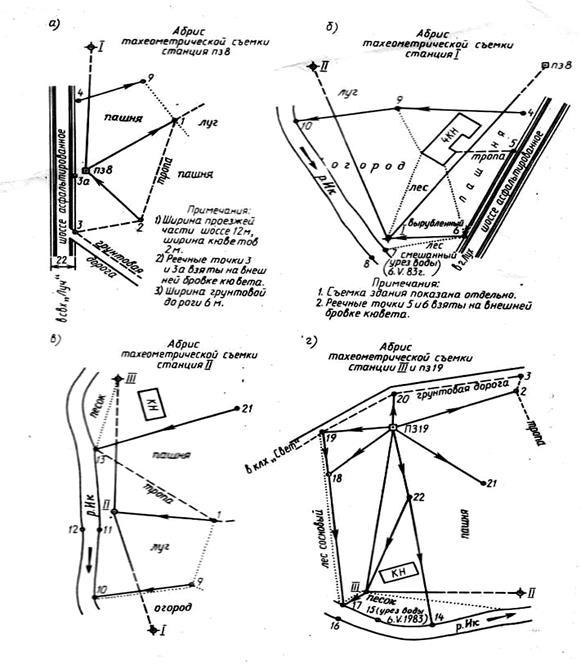
Задание 3. Составление топографического плана строительной площадки
По данным полевых измерений составить и вычертить топографический план строительной площадки в масштабе 1:2000 с высотой сечения рельефа 1м.
Работа состоит из следующих этапов: обработка тахеометрического журнала; построение топографического плана.
Исходные данные
1. Для съемки участка на местности между двумя пунктами полигонометрии П38 и П319 был проложен теодолитно-высотный ход. В нем измерены длины всех сторон а на каждой вершине хода – правый по ходу горизонтальный угол и углы наклона
на предыдущую и последующую вершины.

Результаты измерений горизонтальных углов и линий (табл.2), а также тригонометрического нивелирования (табл.4 и 4а) являются общими для всех вариантов.
Таблица 2. Результаты измерений углов и длин сторон хода
Номера вершин
хода
|
Измеренные углы (правые) |
Длины сторон (горизонтальные проложения), м |
°
|
¢
|
| ПЗ 8 |
330 |
59,2 |
| 263,02 |
| I |
50 |
58.5 |
| 239,21 |
| II |
161 |
20.0 |
| 269,80 |
| III |
79 |
02.8 |
| 192,98 |
| ПЗ 19 |
267 |
08,2 |
Известны координаты полигонометрических знаков ПЗ 8 и ПЗ 19 (т.е. начальной и конечной точек хода):
хПЗ 8 = -14,02
уПЗ 8 = +627,98
Вычисление дирекционных углов и румбов сторон хода.
По исходному дирекционному углу а
0 и исправленным значениям углов b хода по формуле для правых углов вычисляют дирекционные углы всех остальных сторон: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180
°
и минус правый (исправленный) угол хода, образованный этими сторонами.
Пример.
а
ПЗ 8-1 = a
0 + 180° -
bПЗ 8C
=  =236гр 40,2мин.-189гр59,2мин=46гр41мин =236гр 40,2мин.-189гр59,2мин=46гр41мин
Для контроля вычисления дирекционных углов следует найти конечный дирекционный угол а
n
по дирекционному углу а
III-ПЗ 19 последней стороны и исправленному углу bПЗ 19 при вершине ПЗ 19
а
n
= а
III-ПЗ 19 + 180° -
bПЗ 19.
Это вычисленное значение аn
должно совпасть с заданным дирекционным углом аn.
При переходе от дирекционных углов а
к румбам r см. табл.1.
Значения дирекционных углов записывают в графу 4 ведомости с точностью до десятых долей минут, а румбов – в графу 5; при этом значения румбов округляют до целых минут.
Вычисление приращений координат.
Приращения координат вычисляют по формулам:
Dх = d cos a
= ±d cos r; Dу = d sin a
= ±d sin r
Задание4 Решение задач по плану строительного участка
Задача1 Определение отметки точки лежащей между горизонталями.
Нм.г.(отметка меньшей горизонтали)=185
h (заложение)=1м
а (расстояние до меньшей горизонтали) = х 20=
S (расстояние между горизонталями) = м х 20= м
На= + х 1/ м= м
Задача2 Определение уклона ВС
h=1м
d= м
i=
h/ d=1/ =
Задача3 Построение линии ПЗ8-10 с уклоном 0,02
|