|
Данная статья является продолжением работы
«Алгоритм решения Диофантовых уравнений».
Нижегородская область
Г. Заволжье
Белотелов В.Д.
2009 год

Подход к решению уравнений
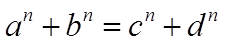 (1)
(1)
 (2)
(2)
Сейчас данные уравнения, насколько мне известно, решены для n
=4.
Т.е. доказано наличие для каждого из уравнений бесконечного количества сочетаний натуральных чисел a
, b
, c
, d
удовлетворяющим условиям равенств уравнений (1), (2)
.
Причём доказательства основаны на компьютерном поиске данных чисел. Нашли компьютерным расчётом для n
=4, отлично - теперь сделайте тоже самое для n
=5 и т.д., т.к. даже для n
=1000 в целом проблема не будет закрыта.
Мне кажется, что есть общий подход к доказательству утверждения о существовании равенств в уравнениях (1), (2)
при любых n
®
¥
.
Я сомневаюсь, что мои рассуждения сойдут за доказательства, но направление, может быть, окажется верным.
I
.
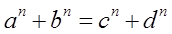
Существует наличие сочетаний a
, b
, c
, d
на чётность и нечётность.
Разберу одну возможность, - пусть все числа a
, b
, c
, d
будут чётными.
А далее буду использовать алгоритм решения Диофантовых уравнений.
Составлю систему уравнений. Бумагу экономить не буду, - распишу подробно.
 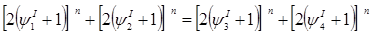
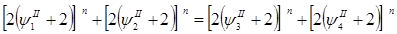
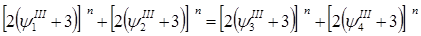
………………………………………………………………. (3)

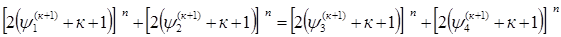
В этих уравнениях пусть  1
> 1
>  3
> 3
>  4
> 4
>  2
– очевидное предположение. 2
– очевидное предположение.
Произведу в уравнениях системы сокращения на 2
n
и члены с  2
перенесу в правую часть уравнений, а члены с 2
перенесу в правую часть уравнений, а члены с  3
– в левую. 3
– в левую.
Сокращением же на 2
n
от чётных значений a
, b
, c
, d
уравнения системы переведены в значения всего натурального ряда.

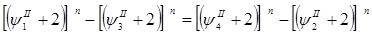
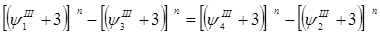
…………………………………………………….
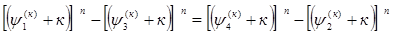
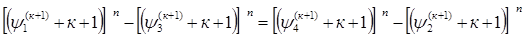
Далее используются формулы разности степеней.
 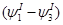 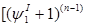 +…..+ +…..+ = =  +…..+ +…..+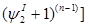
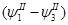 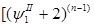 +…..+ +…..+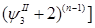 = = 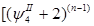 +….+ +….+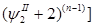
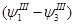 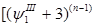 +...+ +...+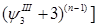 = =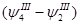 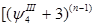 +…+ +…+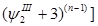
………………………………………………………………. (4)
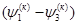  +...+ +...+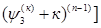 = =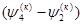 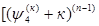 +..+ +..+
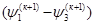 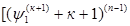 +…..+ +…..+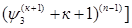 = =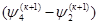  +…..+ +…..+
Т.к. 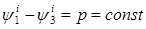 , ,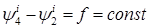 , система (4)
примет вид: , система (4)
примет вид:
 p p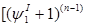 +…..+ +…..+ =f =f +…..+ +…..+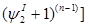
p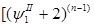 +…..+ +…..+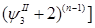 = f = f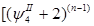 +…..+ +…..+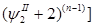
p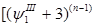 +…..+ +…..+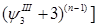 = f = f 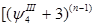 +…..+ +…..+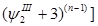 …………………………………………………. ………………………………………………….
p +…..+ +…..+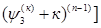 = f = f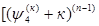 +…..+ +…..+
p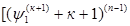 +..+ +..+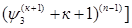 =f =f +…+ +…+
Т.е. у каждого уравнения начальной системы уравнений (3)
произведено понижение формы.
Ну и конечно же доказательство надо вести не от n
к n
-1
, а наоборот, - от n
=2
поэтапно к n
®
¥
.
Уравнение (2)
доказывается аналогичным образом.
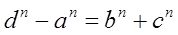 и т.д.
и т.д.
Мне в вышеизложенное и самому не на все 100% верится.
Поэтому я взываю к коллективному разуму.
Главное сомнение же вот в чём:
В таком разе все уравнения с нечётным числом членов решений в натуральных числах не будут иметь, ну или не так строго, могут не иметь.
Т.к. нет понижения формы у одного из членов уравнения.
Как, например, у уравнения (2)
бесконечное число сочетаний натуральных чисел a
, b
, c
, d
существует, тогда, как у уравнения
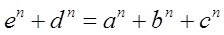 таких сочетаний может и не быть.
таких сочетаний может и не быть.
И без компьютерного расчёта, хотя бы для n
=3
, не обойтись, и если взять мои утверждения, и очень убедительные контрдоводы кого-либо другого.
|