РЕФЕРАТ НА ТЕМУ:
«Ряды динамики»
Изменение социально-экономических явлений во времени изучается статистикой методом построения и анализа динамических рядов.
 Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности. Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности.
Каждый динамический ряд содержит две составляющие:
1) показатели периодов времени (годы, кварталы, месяцы, дни или даты);
2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют
 уровнями ряда. уровнями ряда.
Уровни ряда выражаются как абсолютными, так и средними или относительными величинами. В зависимости от характера показателей строят динамические ряды абсолютных, относительных и средних величин. Ряды динамики из относительных и средних величин строят на основе производных рядов абсолютных величин. Различают интервальные и моментные ряды динамики.
 Динамический интервальный ряд содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объем явления за более длительный период, или так называемые накопленные итоги. Динамический интервальный ряд содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объем явления за более длительный период, или так называемые накопленные итоги.
 Динамический моментный ряд отражает значения показателей на определенный момент времени (дату времени). В моментных рядах исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. Накопленные итоги здесь не рассчитываются. Динамический моментный ряд отражает значения показателей на определенный момент времени (дату времени). В моментных рядах исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. Накопленные итоги здесь не рассчитываются.
Важнейшим условием правильного построения динамических рядов является
 сопоставимость уровней рядов, относящихся к различным периодам. Уровни должны быть представлены в однородных величинах, должна иметь место одинаковая полнота охвата различных частей явления. сопоставимость уровней рядов, относящихся к различным периодам. Уровни должны быть представлены в однородных величинах, должна иметь место одинаковая полнота охвата различных частей явления.
Для того, чтобы избежать искажения реальной динамики, в статистическом исследовании проводятся предварительные расчеты (смыкание рядов динамики), которые предшествуют статистическому анализу динамических рядов. Под
 смыканием рядов динамики понимается объединение в один ряд двух и более рядов, уровни которых рассчитаны по разной методологии или не соответствуют территориальным границам и т.д. Смыкание рядов динамики может предполагать также приведение абсолютных уровней рядов динамики к общему основанию, что нивелирует несопоставимость уровней рядов динамики. смыканием рядов динамики понимается объединение в один ряд двух и более рядов, уровни которых рассчитаны по разной методологии или не соответствуют территориальным границам и т.д. Смыкание рядов динамики может предполагать также приведение абсолютных уровней рядов динамики к общему основанию, что нивелирует несопоставимость уровней рядов динамики.
9.2.
Показатели изменений уровней динамических рядов
Для характеристики интенсивности развития во времени используются статистические показатели, получаемые сравнением уровней между собой, в результате чего получаем систему абсолютных и относительных показателей динамики: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение 1% прироста. Для характеристики интенсивности развития за длительный период рассчитываются средние показатели: средний уровень ряда, средний абсолютный прирост, средний коэффициент роста, средний темп роста, средний темп прироста, среднее абсолютное значение 1% прироста.
Если в ходе исследования необходимо сравнить несколько последовательных уровней, то можно получить или сравнение с постоянной базой (базисные показатели), или сравнение с переменной базой (цепные показатели).
 Базисные показатели характеризуют итоговый результат всех изменений в уровнях ряда от периода базисного уровня до данного (i-го) периода. Базисные показатели характеризуют итоговый результат всех изменений в уровнях ряда от периода базисного уровня до данного (i-го) периода.
 Цепные показатели характеризуют интенсивность изменения уровня от одного периода к другому в пределах того промежутка времени, который исследуется. Цепные показатели характеризуют интенсивность изменения уровня от одного периода к другому в пределах того промежутка времени, который исследуется.
 Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения. Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.
Абсолютный прирост (базисный)
 (9.1) (9.1)
где yi
- уровень сравниваемого периода; y0
- уровень базисного периода.
Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,
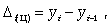 (9.2) (9.2)
где yi
- уровень сравниваемого периода; yi-1
- уровень предшествующего периода.
 Коэффициент роста Ki
определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста. Коэффициент роста Ki
определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.
Коэффициент роста базисный
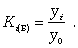 (9.3) (9.3)
Коэффициент роста цепной
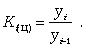 (9.4) (9.4)
 Темп роста Темп роста
 (9.5) (9.5)
 Темп прироста ТП
определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному. Темп прироста ТП
определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.
Темп прироста базисный
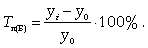 (9.6) (9.6)
Темп прироста цепной
 (9.7) (9.7)
Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей):
1) Тп
= Тр
- 100%; 2) Тп
= Ki
- 1. (9.8)
Абсолютное значение одного процента прироста Ai
. Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.
Данный показатель рассчитывают по формуле
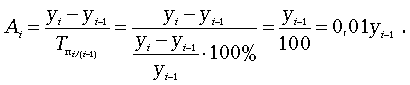 (9.9) (9.9)
Для характеристики динамики изучаемого явления за продолжительный период рассчитывают группу средних показателей динамики. Можно выделить две категории показателей в этой группе: а) средние уровни ряда; б) средние показатели изменения уровней ряда.
 Средние уровни ряда рассчитываются в зависимости от вида временного ряда. Средние уровни ряда рассчитываются в зависимости от вида временного ряда.
Для интервального ряда динамики абсолютных показателей средний уровень ряда рассчитывается по формуле простой средней арифметической:
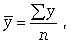 (9.10) (9.10)
где n - число уровней ряда.
Для
 моментного динамического ряда средний уровень определяется следующим образом. моментного динамического ряда средний уровень определяется следующим образом.
Средний уровень моментного ряда с равными интервалами рассчитывается по формуле средней хронологической:
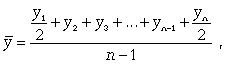 (9.11) (9.11)
где n - число дат.
Средний уровень моментного ряда с неравными интервалами рассчитывается по формуле средней арифметической взвешенной, где в качестве весов берется продолжительность промежутков времени между временными моментами изменений в уровнях динамического ряда:
 (9.12) (9.12)
где t - продолжительность периода (дни, месяцы), в течение которого уровень не изменялся.
Средний абсолютный прирост (средняя скорость роста) определяется как средняя арифметическая из показателей скорости роста за отдельные периоды времени:
 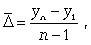 (9.13) (9.13)
где yn
- конечный уровень ряда; y1
- начальный уровень ряда.
Средний коэффициент роста (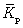 ) рассчитывается по формуле средней геометрической из показателей коэффициентов роста за отдельные периоды: ) рассчитывается по формуле средней геометрической из показателей коэффициентов роста за отдельные периоды:
 (9.14) (9.14)
где Кр1
, Кр2
, ..., Кр n-1
- коэффициенты роста по сравнению с предыдущим периодом; n - число уровней ряда.
Средний коэффициент роста можно определить иначе:
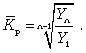 (9.15) (9.15)
Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:
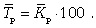 (9.16) (9.16)
Средний темп прироста 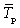 , %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу: , %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу:
 (9.17) (9.17)
Среднее абсолютное значение 1% прироста можно рассчитать по формуле
 (9.18) (9.18)
9.3.
Способы обработки динамического ряда
В ходе обработки динамического ряда важнейшей задачей является выявление основной тенденции развития явления (тренда) и сглаживание случайных колебаний. Для решения этой задачи в статистике существуют особые способы, которые называют методами выравнивания.
Выделяют три основных способа обработки динамического ряда:
а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала;
б) метод скользящей средней;
в) аналитическое выравнивание (выравнивание по аналитическим формулам).
 Укрупнение интервалов - наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней. Укрупнение интервалов - наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней.
По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев расcчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.
 Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом: Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом:
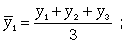   (9.19) (9.19)
При четных периодах скользящей средней можно центрировать данные, т.е. определять среднюю из найденных средних. К примеру, если скользящая исчисляется с продолжительностью периода, равной 2, то центрированные средние можно определить так:
  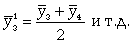 (9.20) (9.20)
Первую рассчитанную центрированную относят ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче на (m - 1)/2, где m - число уровней интервала.
Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является
 аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы. аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы.
Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:
1) используя полусумму уровней, расположенных рядом с интерполируемыми;
2) по среднему абсолютному приросту;
3) по темпу роста.
Способ определения количественных значений за пределами ряда называют
 экстраполяцией. Экстраполирование используется для прогнозирования тех факторов, которые не только в прошлом и настоящем обусловливают развитие явления, но и могут оказать влияние на его развитие в будущем. экстраполяцией. Экстраполирование используется для прогнозирования тех факторов, которые не только в прошлом и настоящем обусловливают развитие явления, но и могут оказать влияние на его развитие в будущем.
Экстраполировать можно по средней арифметической, по среднему абсолютному приросту, по среднему темпу роста.
При аналитическом выравнивании может иметь место
 автокорреляция, под которой понимается зависимость между соседними членами динамического ряда. Автокорреляцию можно установить с помощью перемещения уровня на одну дату. Коэффициент автокорреляции вычисляется по формуле автокорреляция, под которой понимается зависимость между соседними членами динамического ряда. Автокорреляцию можно установить с помощью перемещения уровня на одну дату. Коэффициент автокорреляции вычисляется по формуле
 (9.21) (9.21)
Автокорреляцию в рядах можно устранить, коррелируя не сами уровни, а так называемые остаточные величины (разность эмпирических и теоретических уровней). В этом случае корреляцию между остаточными величинами можно определить по формуле
 (9.22) (9.22)
Анализ
 рядов динамики предполагает и исследование сезонной неравномерности (сезонных колебаний), под которыми понимают устойчивые внутригодовые колебания, причиной которых являются многочисленные факторы, в том числе и природно-климатические. Сезонные колебания измеряются с помощью индексов сезонности, которые рассчитываются двумя способами в зависимости от характера динамического развития. рядов динамики предполагает и исследование сезонной неравномерности (сезонных колебаний), под которыми понимают устойчивые внутригодовые колебания, причиной которых являются многочисленные факторы, в том числе и природно-климатические. Сезонные колебания измеряются с помощью индексов сезонности, которые рассчитываются двумя способами в зависимости от характера динамического развития.
При относительно неизменном годовом уровне явления индекс сезонности можно рассчитать как процентное отношение средней величины из фактических уровней одноименных месяцев к общему среднему уровню за исследуемый период:
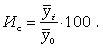 (9.23) (9.23)
В условиях изменчивости годового уровня индекс сезонности определяется как процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев:
 (9.24) (9.24)
Массовые явления, как видели в предыдущих темах, развиваются в пространстве и во времени. Изучение происходящих при этом изменений является одной из важнейших задач статистики.
Процесс развития массового явления во времени принято возникать динамикой, а а показатели, характеризующие это развитие – статистическими рядами динамики. Следовательно:
Рядами динамики называются статистические данные, отображающие развитие явления в последовательные моменты или периоды времени.
Дело в том, что изменения массового явления во времени есть результат взаимодействия разнообразных причин и условий. Отсюда динамика отрицает совокупное действие их через время как собирательный фактор всех других.
В любом ряду динамики имеется два основных элемента: 1) показатель времени t; 2) соответствующие им уровни ряда (уровни развития изучаемого явления) .
В качестве показателя времени в рядах динамики выступают или определенные даты (моменты) времени, или отдельные периоды времени (годы, кварталы, месяца, сутки).
Уровни рядов динамики количественную оценку (меру) развития во времени исследуемого явления. Они могут выражаться абсолютными, относительными, средними или приростными величинами.
Ряды динамики, как правило, представляют в виде таблицы или графически. При графическом изображении ряда динамики (динамического ряда) на оси абсцисс строится шкала времени, а на оси ординат – шкала уравнений ряда (арифметическая или иногда логарифмическая). Изучение рядов динамики осуществляется в разных направлениях анализа состояния .
Закономерности в изменении уравнений ряда в одних проявляется довольно наглядно, в других они могут затушевываться влиянием случайных или других причин. Во всех случаях одной из первых задач статистики исследования является выявление основной тенденции (основного направления) изменения уровней ряда, именуемой «трендом» а чаще количественная оценка темпов развития.
С помощью рядов динамики развития массовых явлений изучаются в следующих основных направлениях: 1) характеристики уровней развития изучаемых явлений во времени; 2) изменение динамики изучаемых явлений посредством системы статистических показателей; 3) выявление и количественная оценка основных тенденций развития (периоды); 4) изучение периодических колебаний: 5) интерполяция и дистрополяция
Ряды динамики различаются по видам.
а) В зависимости от формы выражения уровней (или вида приводимых обобщающих показателей) ряды динамики обычно подразделяют на ряды
1) абсолютных 2) относительных 3) средних 4) приростных величин (показателей).
Исходными, первоначальными являются ряды динамики абсолютных величин, ряды динамики относительных и средних величин составляются на основе рядов динамики абсолютных величин и рассматриваются как производные.
б) В зависимости от формы выражения показателя времени в статике различают 1) моментные ряды и 2) интервальные ряды.
Моментные ряды: динамически отображают состояние изучаемых явлений на определенные даты (моменты) вмени Например, на начало года, или квартала, ли месяца. Так основные фонды учитываются по состоянию на 1-е число каждого месяца, перепись населения страны проводится по состоянию на критический момент времени.
В моментных рядах динамики период месяц датами (моментами времени ) называются интервалами ряда. Величина интервала зависит от характера явлений: для явлений, быстро изменяющихся, ряды динамики должны иметь более короткие интервалы.
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть работников предприятия, составляющих списочную численность на 01.01.1996 г., продолжающая работать в течение данного года, будет отображен в уравнениях последующих периодов (например на 01.02.06, 01.03.06 и т.д.)
Интервальным называется такой ряд, уровни которого характеризуют величину изучаемого показателя за определенный период времени. Например, объем производства продукции можно учитывать за утки, месяц, квартал, полугодие, год и т.д.
В интервальном ряду динамики каждые его уровень складывается из данных за более короткие интервалы времени (суммируя объемы выпуска продукции за каждый день месяца получаем данные за данный месяц и т.д.). Уровни такого ряда можно и дробить. Зная объем производства продукции за месяц и количество рабочих дней путем деления первой величины на вторую можно получить представление о среднесуточном производстве.
Из рассмотренной нетрудно подметить разницу понятия «интервал» и моментном и интервальном рядах. В интервальном ряду интервал – это промежуток, за который обобщены приводимые сведения. В интервальном ряду величина интервала – это накопленный итог учета результатов развития явления во времени.
Необходимо иметь в виду следующее: вид ряда динамики обусловлен не техникой учета, а существом изучаемого явления. Так, состояние явления можно учитывать только моментально, а процесс развития характеризуется по периодам.
Итак, показатели интервальных рядов динамики обладают свойством суммарности, а показатели моментальных рядов такого свойства не имеют. Отсюда порядок величин в интервальном ряду определяется размером интервала (годовой объем продукции в 12 раз больше среднемесячных данных и в 360 раз больше среднесуточных). А в моментальном ряду порядок величин не зависит от размера интервала.
Свойство суммарности интервальных рядов позволяет строить ряды динамики с нарастающими интервалами. Их применение обусловлено потребностями отображения результатов развития изучаемого явления (показателя) не только за данный отдельный период, но и с учетом предшествующих периодов. Например, ввод в действие основных фондов за пятилетку.
Как узнали выше, на основе рядов динамики абсолютных величин могут быть изучены ряды динамики относительных и средних величин. Важнейшими разновидностями статических рядов динамики относительных величин являются ряды, характеризующие темпы динамики, изменение структуры, изменение интервальности.
Нередко в статистических исследованиях в одной таблице приводят ряды динамики абсолютных, относительных и средних величин.
Несопоставимость статистических данных во времени (уровней рядов динамики) может быть обусловлена различными причинами:
- 1) различная система охвата явления статистическими наблюдениями (например, изменение территории, к которой отнесены те или иные показатели);
- 2) разновидность показаний времени (например, учет осуществляется на 1 октября, а затем по состоянию на 1 января);
- 3) неоднородность состава изучаемой совокупности во времени;
- 4) изменения в методике первичного учета и обобщения цеховой информации или в методике расчета показателей;
- 5) различия применяемых в отдельные периоды единиц измерения, цен и т.п.
- 6) различная продолжительность периодов, к которым относятся уровни;
- 7) несовершенство методологии систематического наблюдения и др.
Вопрос о обеспечении сопоставимости может решаться по-разному в зависимости от целей исследования и причин возникновения непоправимости. Для обеспечения сопоставимости осуществляются дополнительные расчеты; изучаются все изменения, происшедшие за анализируемый период в пределах явлений. Например, данные за прошлые годы при территориальных изменениях пересчитываются в новых границах. Аналогично поступают при изменении в методах расчетов показателей, изменении цен и т.д.
Один и тот же ряд динамики для одних цепей является сопоставимым, а для других может быть несопоставимым.
Следовательно, прежде чем анализировать ряды динамики, надо исходя из цели исследования убедиться в сопоставимости уровней ряда и, если имеет место несопоставимость, добиться, при возможности сопоставимости дополнительными расчетами.
Одним из приемов обеспечения сопоставимость рядов динамики является так называемо смыкание рядов динамики.
Под смыканием рядов динамики понимают объединение в один ряд (более длинный) двух или несомых рядов, уровни которых исчислены по разной методологии или в разных границах. При этом для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имеешь данные, исчисленные по разной методологии (или в разных границах).
Для переходного периода определяется коэффициент соотношения двух уровней (отыщите уровни по старой методологии или границе и уровни по новой методологии или границе). Разделив этот коэффициент уровни первого ряда (по старой методологии или территории), можно построить ряд динамики сопоставимых уровней (объединяющих уровни рассматриваемых рядов).
Для количественной оценки рядов динамики применяются различные статистические показатели (характеристики):
- 1) начальный, конечный и средний уровень ряда;
- 2) статистические показатели направления размера изменений уровней ряда во времени;
- 3) средние величины в рядах динамики;
- 4) основная тенденция развития (тренд) и оценка сезонных колебаний;
- 5) Каждый ряд динамики состоит из n-ого числа варьирующих во времени уровней (показателей).
Различают начальный уровень (y1), показывающий величину первого члена ряда и конечный (yn), показывающий величину последнего члена ряда.
Обычно анализ рядов динамики начинается с определения среднего уровня.
Средний уровень ряда даёт обобщённую характеристику показателя за весь период, охватываемый рядом динамики.
Средний уровень в интервальном и моментальном рядах динамики определяется по разному.
В интервальном ряду с равными периодами (интервалами) средний уровень рассчитывается по формуле простой средней арифметической.
Например, средний уровень добычи нефти, выплавки чугуна и так далее ежегодно (за месяц) за рассматриваемый период.
Таким образом, чтобы исчислить среднюю из интервального ряда, нужно сложить члены ряда и разделить полученную сумму на их число.
Эта средняя известна в статистике как Средняя характеристическая для моментального ряда.
Таким образом, средняя хронологическая из моментального ряда динамики равняется сумме показателей этого ряда (при этом начальный и конечный уровни должны быть взяты в половинном размере), делённой на число показателей без одного.
В случае неравных интервалов времени между фактами (моментами, датами) средний уровень ряда определяется в следующей последовательности: 1) определяется средние за интервалы, ограниченные двумя датами; 2) расчёт из них общей средней; при этом средние за более длительные интервалы должны быть взяты с весами, кратные их длине.
Пример. Численность работников предприятия составила на 1.01 - 1100 человек; на 15.02 – 1120 человек; на 22.03 – 1150 человек, на 31.03 тоже 1150 человек.
б) Средний уровень ряда, как любая средняя величина, является обобщающим показателем. Вместе с тем при изучении рядов динамики важно проследить за направлением и размером изменений уровней во времени. С этой целью для динамических рядов (рядов динамики) рассчитываются такие статические показатели, как: 1) темпы роста. 2) абсолютные приросты. 3) темпы прироста. 4) абсолютная величина одного процента роста.
Темпы роста(темпы динамики ТР) – это относительный статистический показатель, определяемый как отношение одного уровня к другому одного и того же и показывающий во сколько раз один уровень больше(меньше) другого.
В зависимости от выбора базы сравнения темпы роста рассчитываются как цепные, когда каждый уровень сопоставляется с уровнем предыдущего периода и как базисные, когда все уровни ряда сопоставляются с уровнем одного какого-то периода, принятого за базу сравнения (как правило, это бывает начальный уровень ряда, но может быть и уровень любого другого периода)
Соответственно цепные темпы роста (Трцi) характеризуют интенсивность развития явления в каждом отдельном периоде, а базисное – интенсивности развития за любой отрезок времени (отделяющий данный уровень от базисного).
В том и другом случае темпы роста могут быть выражены в виде коэффициентов, если основание отношения принимается за единицу, и в виде процентов, если основание принимается за 100.
Между цепным (Трцi) и базисным (Трбi) темпами роста существует непосредственная связь, позволяющая в случае необходимости переходит от одних к другим, то есть от цепных темпов к базисным и наоборот:
1. произведение цепных темпов роста равно базисному
2. результат деления двух базисных темпов роста равны цепному (промежуточному) темпу роста
Показатели темпов облегчают анализ, показывают направления развития: если темпы больше 1 или 100%, то уровни, характеризующие явления, возрастают, если же меньше 1 или 100%, то сокращаются.
Темпы роста поэтому в статистике широко используются при анализе динамики массовых явлений и процессов. Однако темпы роста – это относительная величина и, пользуясь этим для характеристики интенсивности и направления развития никогда не стоит забывать об абсолютных уровнях развития, которые скрываются за темпами роста. Например, рост числа абонентов сети ГТС в 2 раза соответственно с 10 тысячами и 100 тысячами имеет различные экономические содержания.
Поэтому типы роста дополняют показателями об абсолютных и относительных приростах, абсолютным значениям 1% прироста.
Абсолютный прирост (∆y) рассчитывается как разность между двумя уровнями ряда и выражается в единицах измерения исходной информации.
Базисный абсолютный прирост (∆yб) исчисляется как разность между сравниваемым уровнем yi и уровнем, принятым за постоянную базу сравнения y0 по формуле .
Цепной абсолютный прирост (∆уц) – это разность между сравниваемым уровнем yi и уровнем, который ему предшествует yi-1
Абсолютный прирост показывает на смысл единиц (по принятой для уровней рода единиц измерения), увеличивается или уменьшается уровень, характеризует изучаемое явление, соответственно с начал рассматриваемого или предшествующего периода.
Следовательно абсолютный прирост может иметь знак “+” (при увеличении уровней) или “-” (при уменьшении уровней).
Для относительной оценки значений абсолютных приростов рассчитываются показатели цепных приростов.
Средние показатели в рядах динамики
При анализе развития изучаемого явления во времени (или рядов динамики) часто возникает необходимость дать особенную характеристику направления и интенсивности процесса развития за длительный период. Для этого исчисляю также обобщающие статистические показатели, как средние величины . Средние величины могут рассчитываться для каждого из рассмотренных выше статистических показателей динамики.
- 1) Один вид средней величины мы уже рассмотрели в 3-м вопросе в составе 1-й группы статических показателей, используемых статистикой для анализа рядов динамики. Речь идёт о среднем уровне ряда, который характеризует статическую величину абсолютных уровней.
- 2) Средней абсолютный прирост (∆ )представляет собой обобщённую статистическую характеристику индивидуальных (цепных) абсолютных приростов и может определяться по следующим формулам:
- 3) Средний темп роста является обобщающей характеристикой индивидуальных (цепных) темпов роста ряда динамики или накопленного изменения уровня явления за продолжительный период времени.
Средний темп роста может быть рассчитан с использованием различных формул:
а) как средняя геометрическая из цепных темпов роста (в коэффициентах)
Расчёт среднего темпа роста производят с использованием специальных таблиц, с помощью логарифмов и ЭВМ.
Средний темп роста имеет смысл рассчитываться только в тех случаях, кода на протяжении всех лет происходит лишь непрерывный рост, лишь непрерывное сокращение.
Однако на самом деле по второму периоду объём продукции снижен на 6%. Следовательно, вывод о приросте продукции за каждый период в среднем на 2.8% является неправильным, ошибочным.
4) Средние темпы роста (снижения) рассчитываются на основе средних темпов роста ряда с возрастающими (убывающими) уровнями путём высчитывания их средних 1 или 100 %
Как и при расчёте среднего темпа роста, средние темпы прироста (снижения) рассчитываются по рядам, имеющим одно направление развития, и будут в этом отношении качественно однородными.
В тех случаях, когда целесообразно определить средний темп динамики на основе резко колеблющихся уровней рядов динамики (например, урожайность сельхозкультур) расчёты правильнее производить на основе сравнения средних уровней за определенные временные отрезки (например, пятилетние периоды).
Анализ взаимосвязанных рядов динамики
.
В простейших случаях для характеристики взаимосвязи двух или более рядов их
приводят к общему основанию , для чего берут в качестве базисных уровни за
один и тот же период и исчисляют коэффициенты опережения по темпам роста или
прироста .
Коэффициенты опережения по темпам роста – это отношение темпов роста (цепных
или базисных) одного ряда к соответствующим по времени темпам роста (также
цепным или базисным) другого ряда . Аналогично находятся и коэффициенты
опережения по темпам прироста .
Анализ взаимосвязанных рядов представляет наибольшую сложность при изучении
временных последовательностей . Однако нередко совпадение общих тенденций
развития может быть вызвано не взаимной связью , а прочими неучитываемыми
факторами . Поэтому в сопоставляемых рядах предварительно следует избавиться
от влияния существующих в них тенденций , а после этого провести анализ
взаимосвязи по отклонениям от тренда . Исследование включает проверку рядов
динамики (отклонений) на автокорреляцию и установление связи между признаками
.
Под автокорреляцией понимается зависимость последующих уровней ряда от
предыдущих . Проверка на наличие автокорреляции осуществляется по критерию
Дарбина – Уотсона (формула 39) :
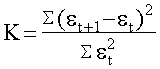 , (39)
, (39)
где  -- отклонение
-- отклонение
фактического уровня ряда в точке t от теоретического (выравненного) значения .
При К = 0 имеется полная положительная автокорреляция , при К = 2
автокорреляция отсутствует , при К = 4 – полная отрицательная автокорреляция
. Прежде чем оценивать взаимосвязь , автокорреляцию необходимо исключить .
Это можно сделать тремя способами .
1. Исключение тренда с авторегрессией. Для каждого из взаимосвязанных рядов
динамики Х и У получают уравнение тренда (формулы 40) :
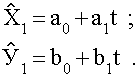 (40)
(40)
Далее выполняют переход к новым рядам динамики , построенным из отклонений от
трендов , рассчитанным по формулам 41 :
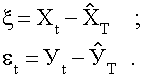 (41)
(41)
Для последовательностей 
выполняется проверка на автокорреляцию по критерию Дарбина – Уотсона . Если
значение К близко к 2 , то данный ряд отклонений оставляют без изменений . Если
же К заметно отличается от 2 , то по такому ряду находят параметры уравнения
авторегрессии по формулам 42 :
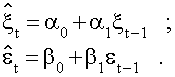 (42)
(42)
Более полные уравнения авторегрессии можно получить на основе анализа
автокорреляционной функции , когда определяются число параметров (
) и соответствующие этим параметрам величины шагов .
Далее по формуле 43 подсчитываются новые остатки :
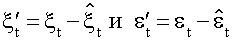 (t = 1, ... , Т) (43)
(t = 1, ... , Т) (43)
и , по формуле 44, коэффициент корреляции признаков :
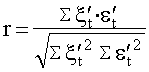 . (44)
. (44)
2. Корреляция первых разностей . От исходных рядов динамики Х и У переходят к
новым , построенным по первым разностям (формулы 45) :
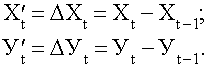 (45)
(45)
По DХ и DУ определяют по формуле 46 направление и силу связи в регрессии:
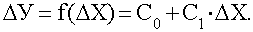 (46)
(46)
3. Включение времени в уравнение связи : 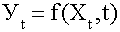 .
.
В простейших случаях уравнение выглядит следующим образом (формула 47):
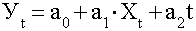 (47)
(47)
Из перечисленных методов исключения автокорреляции наиболее простым является
второй , однако более эффективен первый .
|