Методи обробки ЕЕГ
1. Картування
Спектральний аналіз вихідної ЕЕГ часто замінюється аналізом топографічних карт (рис. 1), які показують розподіл спектральної потужності за смугами спектра.

Рисунок 1 – Картування ЕЕГ
Можливі переваги цього підходу полягають у тому, що деякі задачі розпізнавання, згідно з даними психології, розв'язуються людиною краще на основі візуально-просторового сприйняття.
Для одержання карти розподілу потужності у визначеному спектральному діапазоні роблять обчислення спектрів потужності для кожного з відведень.
Потім усі значення, що лежать просторово між електродами, обчислюють методом лінійної інтерполяції: спектральна щільність потужності у визначеній смузі кодується для кожної точки інтенсивністю сірого кольору при чорно-білому дисплеї чи кольором у заданій колірній шкалі при кольоровому дисплеї.
На екрані виходить зображення голови досліджуваного (як правило, вид зверху), на якому варіації кольору чи інтенсивності відповідають потужності спектральної смуги у відповідній області. Зазвичай використовується система подання спектральної потужності в шести основних спектральних смугах ЕЕГ у вигляді кольорових карт з 11 рівнями кодування інтенсивності. Деякі автори відзначають, що суб'єктивно патологічні асиметрії в топографічних картах сприймаються більш переконливо, ніж на звичайній ЕЕГ. Нині деякі фірми роблять комерційні пристрої для генерування топографічних карт ЕЕГ.
Крім того, використовуються також топографічні карти амплітуд ЕЕГ. Амплітудне картування ЕЕГ (КАЕЕГ) являє собою карту миттєвого розподілу різниці потенціалів на поверхні голови. Оскільки просторова ЕЕГ у будь-якій точці реєстрації являє собою стохастичний процес, то й будь-який миттєвий розподіл потенціалу, що фіксується топографічною картою, є нерепрезентативним. Єдиним адекватним застосуванням КАЕЕГ є використання його для оцінки динаміки виникнення і поширення феноменів ЕЕГ (насамперед епілептиформних паттернів «спайк», «спайк-хвиля», гострі хвилі). Аналіз послідовних карт потенціалу, що показують його розподіл через задані короткі інтервали часу, дозволяє одержати наочне уявлення про місце виникнення феномена, що нас цікавить, його поширення по мозку. Слід зазначити, що цей метод не дає нової інформації, яку не можна було б вилучити з «сирого» запису ЕЕГ. Цей метод подає інформацію у більш наочній формі. Програма побудови карт спектральної щільності потужності за заданими смугами спектра є більш адекватною для задач клінічної діагностики.
Метод картування знаходить все більш широке поширення як метод подання електроенцефалографічних даних у клінічних діагностичних лабораторіях. При цьому іноді йдеться про те, щоб певною мірою замінити візуальний аналіз вихідної ЕЕГ аналізом топографічних карт розподілу потужності по смугах спектра, співвідносин сум спектральних щільностей потужності в різних діапазонах частот (наприклад,  ) чи ж розподіл амплітуд деяких феноменів ЕЕГ, насамперед епілептиформної активності. У численних публікаціях не припиняється дискусія про недоліки і переваги цього методу порівняно з іншими методами дослідження. ) чи ж розподіл амплітуд деяких феноменів ЕЕГ, насамперед епілептиформної активності. У численних публікаціях не припиняється дискусія про недоліки і переваги цього методу порівняно з іншими методами дослідження.
Можливості точної кількісної оцінки параметрів ЕЕГ дозволяють більш детально й об'єктивно оцінювати зміни функціонального стану мозку. Отже, метод картування дозволяє ефективно проводити діагностику. З іншого боку, немає цілком переконливих і статистично безперечних доказів її переваги порівняно з даними аналізу «сирої» ЕЕГ.
2. Згладжування методом Калмана
Для обробки ЕЕГ з метою очищення від шуму застосовується згладжування за допомогою фільтра Калмана (ФК). ФК призначений для оптимального оцінювання лінійної динамічної системи. Ідея синтезу ФК полягає у знаходженні рекурентного алгоритму у вигляді різницевого рівняння (у випадку системи з дискретним часом) чи диференційного рівняння (у випадку системи з безперервним часом). Кожна наступна оцінка стану системи отримується на основі виміру і попередньої оцінки за умови мінімуму дисперсії помилки.
Розглянемо випадок дискретного часу. Рівняння спостереження має вигляд:
 . (1) . (1)
У свою чергу рівняння повідомлення подається як:
 , ,  , (2) , (2)
де  – задані функції часу; – задані функції часу;
 – дискретні білі гауссові шуми з нульовими математичними очікуваннями і дисперсіями – дискретні білі гауссові шуми з нульовими математичними очікуваннями і дисперсіями  і і  відповідно; відповідно;
 – нормально розподілена випадкова величина. – нормально розподілена випадкова величина.
Система рівнянь ФК має вигляд:
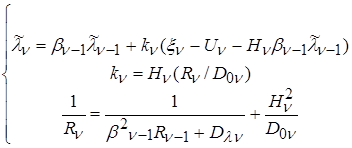 . (3) . (3)
Ця система розв'язується чисельно за допомогою алгоритму, що дозволяє знайти часову залежність процесу за умови мінімуму вихідної дисперсії. На рис. 2 наведені часові залежності ЕЕГ(пунктир) і ЕЕГ, обробленої фільтром Калмана (суцільна).
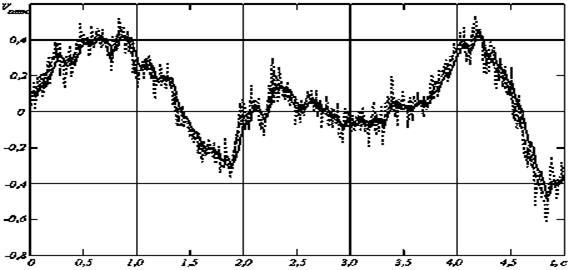
Рисунок 2 – Часові залежності ЕЕГ
Застосуємо до реалізації ЕЕГ і до оброблених ЕЕГ дискетне перетворення Фур'є (ДПФ), що записується у вигляді
 , (4) , (4)
де  – крок за частотою; – крок за частотою;
 – число точок на часовій осі; – число точок на часовій осі;
 – крок за часом; – крок за часом;
 – відліки за частотою; – відліки за частотою;
 – відліки за часом. – відліки за часом.
Отримані спектри наведені на рис. 3, де на графіках показані спектри вихідної ЕЕГ (суцільна), згладженої за допомогою ФК (пунктир). Як видно, видалення шуму фактично являє собою фільтрацію високочастотних складових процесу.
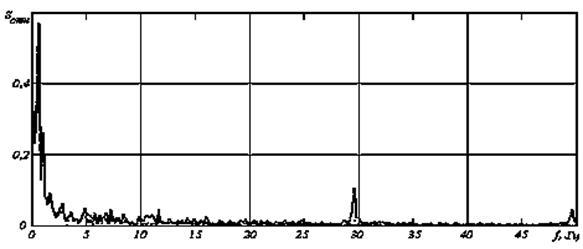
Рисунок 3 – Спектри вихідної ЕЕГ (суцільна), згладженої за допомогою ФК (пунктир)
3. Фазочастотний метод аналізу миттєвих характеристик ЕЕГ
Спектрально-кореляційні методи дозволяють визначити домінування визначених частотних складових на даному відрізку ЕЕГ і за цими даними знайти, зокрема, зону розташування патологічного вогнища. Однак вони не дають можливості детально простежити і чисельно охарактеризувати динаміку зміни структури ЕЕГ у часі, зміну і тривалість ритмів. Фазочастотний метод заснований на представленні випадкового процесу  у вигляді у вигляді  . При цьому випадковий процес . При цьому випадковий процес  розглядається як гармонійне коливання, модульоване за амплітудою і фазою випадковими функціями розглядається як гармонійне коливання, модульоване за амплітудою і фазою випадковими функціями  і і  . Обчислення цих функцій дозволяє спостерігати зміну амплітуди і фази ЕЕГ у часі, а також досліджувати зміну в часі миттєвої і середньої частот коливань, якщо підходити до поняття частоти як похідної фази коливального процесу. Такий метод аналізу дозволяє чисельно охарактеризувати тривалість і частоту зміни окремих ритмів. . Обчислення цих функцій дозволяє спостерігати зміну амплітуди і фази ЕЕГ у часі, а також досліджувати зміну в часі миттєвої і середньої частот коливань, якщо підходити до поняття частоти як похідної фази коливального процесу. Такий метод аналізу дозволяє чисельно охарактеризувати тривалість і частоту зміни окремих ритмів.
Можливість представлення випадкового процесу у вигляді гармонійного коливання, промодульованого випадково за амплітудою і фазою, досить теоретично обґрунтована. Представимо випадковий процес  у формі у формі
 . (5) . (5)
Зв'язок між  , ,  і і  можна встановити за допомогою інтегральних перетворень Гільберта можна встановити за допомогою інтегральних перетворень Гільберта
 , ,  , ,
причому при  беруться головні (у понятті Коші) значення інтегралу. Функція беруться головні (у понятті Коші) значення інтегралу. Функція  називається спряженим процесом стосовно називається спряженим процесом стосовно  . .
Огинаюча процесу  і фаза і фаза  визначаються так: визначаються так:
 , ,  . .
Представлення випадкового процесу у вигляді (5) легко інтерпретувати у випадку вузькосмугових процесів. У цьому випадку велику наочність набуває поняття огинаючої, в яку вписується гармонійне чи майже гармонійне коливання. Крім того, можна визначити миттєву частоту процесу за допомогою співвідношення
 . (6) . (6)
ЕЕГ є широкосмуговим процесом, і в цьому випадку поняття огинаючої не має чіткого фізичного змісту. Середню чи поточну частоту коливального процесу зазвичай визначають за числом періодів в одиницю часу, не користуючись похідною фази. Цими обставинами можна пояснити той факт, що аналіз широкосмугових процесів за допомогою виразу (6) на практиці зазвичай не використовується. Водночас аналіз функції  дозволяє одержати деяку додаткову інформацію про стабільність частотних характеристик, час стаціонарності і характер перехідних режимів у коливальному процесі. дозволяє одержати деяку додаткову інформацію про стабільність частотних характеристик, час стаціонарності і характер перехідних режимів у коливальному процесі.
Введення для широкосмугових процесів поняття поточної частоти шляхом усереднення фазової кривої на деякому інтервалі часу  дає можливість охарактеризувати тривалість і частоту зміни характерних коливань (ритмів у випадку ЕЕГ) у досліджуваному процесі. дає можливість охарактеризувати тривалість і частоту зміни характерних коливань (ритмів у випадку ЕЕГ) у досліджуваному процесі.
Для ілюстрації можливостей методу фазочастотного аналізу на рис. 4 показані відрізки штучно складених реалізацій і відповідні цим реалізаціям фазові і частотні криві. Реалізація, зображена на рис. 4, складена з відрізків синусоїд з різними амплітудами і частотами. З рисунка видно, що фазові залежності в межах синусоїдальних відрізків являють собою прямі лінії, що відповідають коливанням з постійною частотою. Стрибки фаз у коливальному процесі знаходять чітке відображення на фазовій кривій. Відрізкам синусоїд з однаковою частотою, але різними амплітудами відповідає той самий нахил фазової кривої, тобто та сама частота коливань.
Реалізація, показана на рис. 5, отримана шляхом довільного перекручування (модуляції) форми синусоїди накладенням більш високочастотного коливання невеликої амплітуди. Як видно з фазової кривої, наявність високочастотних низькоамплітудних коливань, що модулюють, приводить до перекручування форми фазової кривої та її відхилення від прямої лінії. Однак частота, отримана шляхом згладжування цієї кривої, дорівнює частоті неспотвореної синусоїди. Отже, на фазовій кривій можна виділити частоту високоамплітудного коливання.
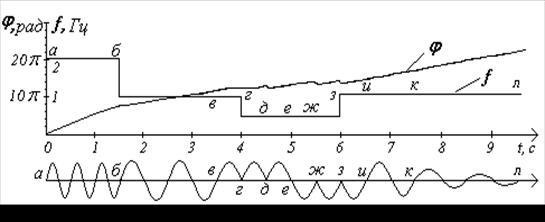
Рисунок 4 – Реалізація, складена з відрізків синусоїд з різними амплітудами і частотами та її фазова й частотні криві
Штучна реалізація, показана на рис. 6, може служити прикладом випадкового слабкокорельованого широкосмугового процесу (на цьому рисунку  і і – амплітудний спектр і автокореляційна функція відповідно). Форма фазової кривої в цьому випадку складна, визначити по ній частотні характеристики процесу можна двома способами. По-перше, згладивши криву в межах відрізків часу – амплітудний спектр і автокореляційна функція відповідно). Форма фазової кривої в цьому випадку складна, визначити по ній частотні характеристики процесу можна двома способами. По-перше, згладивши криву в межах відрізків часу  , протягом яких відрізки кривої добре апроксимуються відрізками прямої, можна одержати значення поточної частоти процесу. , протягом яких відрізки кривої добре апроксимуються відрізками прямої, можна одержати значення поточної частоти процесу.
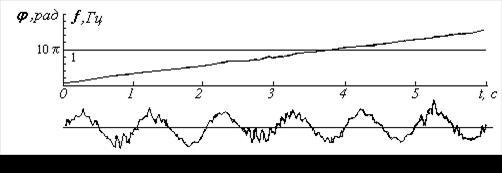
Рисунок 5 – Реалізація, отримана шляхом довільного перетворювання (модуляції) форми синусоїди накладенням більш високочастотного коливання невеликої амплітуди та її фазова й частотні криві
На рис. 6 показана частотна крива, що відповідає такому усередненню.
З урахуванням висновку, зробленого під час розгляду рис. 5, можна сказати, що поточна частота, яка відповідає високоамплітудній низькочастотній складовій спектра коливання за час  , змінюється в невеликих межах. , змінюється в невеликих межах.
Частотна крива на рис. 6 характеризує зміну в часі поточної частоти процесу і горизонтальні площадки на частотній кривій визначаються відрізками часу, протягом яких поточна частота практично не змінюється. В інших можна усереднити усю фазову криву, з'єднавши прямою крайні точки цієї кривої.
У цьому випадку визначення повного приросту фази  за весь аналізований відрізок часу дозволяє знайти деяку середню частоту процесу. за весь аналізований відрізок часу дозволяє знайти деяку середню частоту процесу.

Рисунок 6 – Реалізація ЕЕГ, спектр і функція автокореляції
Розглянемо фазочастотний аналіз ЕЕГ здорових і хворих людей з осередковими ураженнями головного мозку.
На рис. 7 наведені графіки зміни фази ЕЕГ потиличної області правої півкулі мозку здорового випробуваного. На графіку виділені (пунктирними лініями) смуги частот, що відповідають фізіологічним ритмам. Поточні частоти визначалися за фазовою кривою, отриманою при апроксимації відрізків кривої прямими лініями.
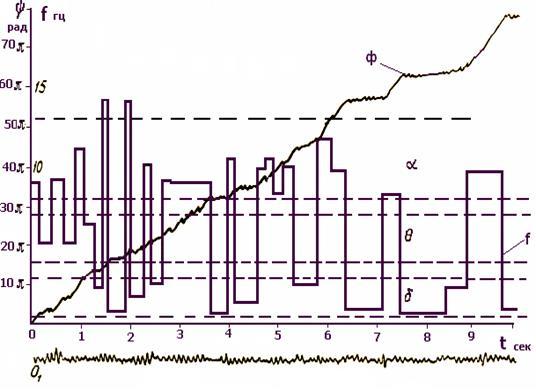
Рисунок 7 – Графіки зміни фази та частоти ЕЕГ потиличної області правої півкулі мозку здорового випробуваного
Під час розгляду рис. 7 насамперед слід звернути увагу на властиву взагалі ЕЕГ особливість поведінки фазових кривих, що полягає в чергуванні чітко виражених ділянок, які надійно апроксимуються прямими лініями. Така поведінка фазових кривих пояснюється наявністю в ЕЕГ ділянок квазігармонічних включень з частотами, що відповідають різним фізіологічним ритмам.
Фазочастотний аналіз ЕЕГ виділяє лише ті ділянки високочастотних ритмів, які виражені самостійно і не накладаються на низькочастотні коливання ЕЕГ.
На рис. 8 наведена ЕЕГ хворої з пухлиною довгастого мозку. Фазовий аналіз ЕЕГ потиличної області показує відсутність самостійної та модулюючої альфа-періодики. Звертає на себе увагу домінування повільної активності.
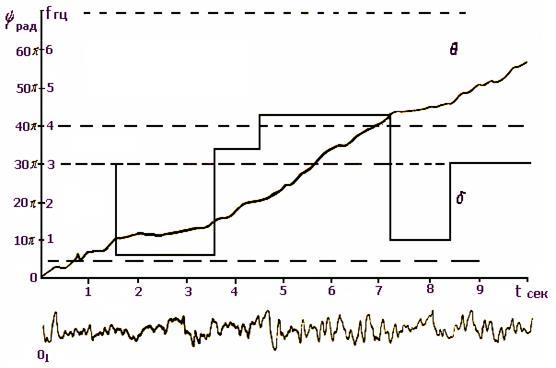
Рисунок 8 – Графіки зміни фази та частоти ЕЕГ хворої з пухлиною довгастого мозку
Фазочастотний метод аналізу ЕЕГ дозволяє простежити за динамікою зміни ЕЕГ, чисельно охарактеризувати тривалість і зміну основних фізіологічних ритмів, а також простежити за зміною частоти в межах кожного ритму. За допомогою цього методу можна простежити зміни в ЕЕГ при патології.
|