| Министерство образования Российской Федерации
Нижегородский государственный университет
Имени Н.И. Лобачевского
Факультет ВМК
Разложение в ряды Тейлора
отчёт по дисциплине:
Информатика и программирование
Выполнила:
Студентка Репина Инна Сергеевна,
(в/о)
Проверила:
Нижний Новгород
2006
Содержание
1.
Введение……………………………………………………….. стр. 3
2.
Постановка задачи................................................................ стр. 5
3.
Руководство пользователя................................................... стр. 6
4.
Руководство программиста.................................................. стр. 7
5.
Заключение............................................................................ стр. 8
6.
Список литературы .............................................................. стр. 10
7.
Приложение.......................................................................... стр. 11
Введение
Ряд Тейлора – степенной ряд вида:
 , (1)
, (1)
где f
(x
) - функция, имеющая при х
= а
производные всех порядков. Во многих практически важных случаях этот ряд сходится к f
(x
) на некотором интервале с центром в точке а:
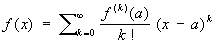 (2)
(2)
(эта формула опубликована в 1715 Б. Тейлором).
Разность Rn
(x
) = f
(x
) - Sn
(x
),
где Sn
(x
) - сумма первых n
+ 1 членов ряда (1), называется остаточным членом Т. р. Формула (2) справедлива, если  . Т. р. можно представить в виде
. Т. р. можно представить в виде
 ,
,
применимом и к функциям многих переменных.
При а
= 0 разложение функции в Т. р. принимает вид:
 ,
,
в частности:
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
 .(7)
.(7)
Ряд (3), являющийся обобщением на случай дробных и отрицательных показателей формулы бинома Ньютона, сходится: при -1< х
< 1, если m
< -1; при -1< x £ 1, если -1< m
< 0; при -1 £ x £ 1, если m
> 0.
Ряды (4), (5) и (6) сходятся при любых значениях х,
ряд (7) сходится при -1< x £ 1.
Функция f
(z
) комплексного переменного z,
регулярная в точке а,
раскладывается в Т. р. по степеням z
- а
внутри круга с центром в точке я и с радиусом, равным расстоянию от а
до ближайшей особой точки функции f
(z
).
Вне этого круга Т. р. расходится, поведение же его на границе круга сходимости может быть весьма сложным. Радиус круга сходимости выражается через коэффициенты Т. р.
Т. р. является мощным аппаратом для исследования функций и для приближённых вычислений. Пэтому данная работа посвящена именно ему.
Постановка задачи
Задача заключается в том, чтобы посчитать через ряд Тейлора функцию и сравнить её значение с значением стандартной функции в паскале.
Предлагается рассмотреть три функции: sin, cos и exp.
Для каждой из них существует разложение в ряд Тейлора.
Разложения:
1. 
2. 
3. 
Бесконечно малыми пренебрежем.
Руководство пользователя
1. Запускаем программу.
На экране появляется главное меню:
1 – sin x
2 – cos x
3 – exp x
4 – Выход
2. Выбираем функцию: синус, косинус или экспонент.
3. Вводим аргумент.
4. Вводим количество слагаемых.
5. Получаем результат и точность в вычислении.
Примечание
Под точностью понимается количество членов ряда.

Главное меню
Руководство программиста
В программе используются переменные процедурного типа.
Точнее, мы присваиваем переменной процедуру, проверяем корректность заданного параметра и потом с помощью переменной процедурного типа вычисляем пошагово в цикле очередной член ряда и прибавляем его к сумме.
В программе функциям передаются следующие параметры: аргумент, точность вычислений (число членов ряда) и переменная процедурного типа, указывающая на функцию, которая возвращает новый член ряда. Функции вычисляют новый член ряда на основе аргумента и номера члена. В функции не передаётся предыдущий член ряда, поскольку результат выполнения этих функций домножается на предыдущий член ряда. Заключение
При большом количестве членов ряда (начиная с 10-14 для разных рядов) погрешность в вычислениях становится настолько мала, что иногда округляется до нуля. При стремлении числа слагаемых в бесконечность погрешность стремится к нулю. В результате мы получаем корректный результат при большем количестве членов ряда.
В результате данной работы была написана программа и были проведены эксперементы, результатами которых явилось:
1.

Sin x
2.
Cos x

3.
Exp
X

Список литературы
1. Л.Д. Кудрявцев «Курс математического анализа»
2. В.Г. Абрамов, Н.П. Трифонов, Г.Н. Трифонова «Введение в язык Паскаль».
Приложение
program teylor;
uses
SysUtils;
var a,x,sum: real;
n,i,answ: integer;
begin
writeln ('Viberite funkciyu');
writeln ('1-sinx');
writeln ('2-cosx');
writeln ('3-expx');
writeln ('4-Vihod');
readln (answ);
writeln ('Vvedite argument i kolichestvo slagaemih');
readln (x,n);
case answ of
1: begin
a:=x;
sum:=a;
for i:=1 to n do
begin
a:=a*(-1)*x*x/(2*i*(2*i+1));
sum:=sum+a;
writeln (i, sum);
end;
writeln ('Pogreshnost', abs(sin(x)-sum));
end;
2: begin
a:=1;
sum:=1;
for i:=1 to n do
begin
a:=a*(-1)*x*x/((2*i)*(2*i-1));
sum:=sum+a;
writeln (i, sum);
end;
writeln ('Pogreshnost', abs(cos(x)-sum));
end;
3: begin
a:=1;
sum:=1;
for i:=1 to n do
begin
a:=a*x/i;
sum:=sum+a;
writeln (i, sum);
end;
writeln ('Pogreshnost', abs(exp(x)-sum));
end;
end{case};
readln;
end.
|