|
Нижегородский Государственный Технический Университет.
Лабораторная работа по физике №2-30.
Экспериментальные исследования диэлектрических
свойств материалов.
Выполнил студент
Группы 99 – ЭТУ
Наумов Антон Николаевич
Проверил:
Н. Новгород 2000г.
Цель работы:
определение диэлектрической проницаемости и поляризационных характеристик различных диэлектриков, изучение электрических свойств полей, в них исследование линейности и дисперсии диэлектрических свойств материалов.
Теоретическая часть:
Схема экспериментальной установки.
В эксперименте используются следующие приборы: два вольтметра PV1 (стрелочный) и PV2 (цифровой), генератор сигналов низкочастотный, макет-схема, на которой установлен резистор R=120 Ом, конденсатор, состоящий из набора пластин различных диэлектриков (толщиной d=2 мм).
Собираем схему, изображенную на РИС. 1. Ставим переключатель SA в положение 1. Подготавливаем к работе и включаем приборы. Подаем с генератора сигнал частоты f=60 кГц и напряжением U=5 В, затем по вольтметру PV1 установить напряжение U1=5 В. Далее, вращая подвижную пластину, измеряем напряжение U2 для конденсатора без диэлектрика и 4-x конденсаторов с диэлектриками одинаковой толщины. При этом напряжение U1 поддерживаем постоянным.
Напряженность поля между пластинами в вакууме Е0
вычисляется по формуле:  где  При внесении пластины в это поле диэлектрик поляризуется и на его поверхности появляются связанные заряды с поверхностной плотностью  . Эти заряды создают в диэлектрике поле  , направленное против внешнего поля  , и имеет величину: 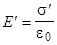 . Результирующее поле:  . В электрическом поле вектор поляризации: , где c - диэлектрическая восприимчивость вещества. Связь модуля вектора поляризации с плотностью связанных зарядов:  .  относительная диэлектрическая проницаемость диэлектрика. Вектор электрической индукции  . Этот вектор определяется только свободными зарядами и вычисляется как  . В рассматриваемой задаче на поверхности диэлектрика их нет. Вектор D связан с вектором Е следующим соотношением  .
Экспериментальная часть:
В данной работе используются формулы:  , где S - площадь пластины конденсатора, d - расстояние между ними. Диэлектрическая проницаемость материала:  . Для емкости конденсатора имеем:  , где U1
- напряжение на RC цепи, U2
- напряжение на сопротивлении R, f - частота переменного сигнала. В плоском конденсаторе напряженность связана с напряжением U1
как:  
Опыт №1.
Измерение диэлектрической проницаемости и характеристик поляризации материалов.
U1
= 5В, R=120Ом, f=60 кГц, d=0,002м.
| Материал
|
U
2
, мВ
|
| Воздух
|
40
|
| Стеклотекстолит
|
97
|
| Фторопласт
|
61
|
| Гетинакс
|
89
|
| Оргстекло
|
76
|
 СВ
=176 пкФ; ССТ
=429 пкФ;
СФП
=270 пкФ; СГН
=393 пкФ; СОС
=336 пкФ;
 ;  ;
 ;  ;
Для гетинакса подсчитаем:
 ;
 ;  ;
 ;  ;
 ;  ;
 ;
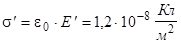Расчет погрешностей:
; 
; 
;
;
;
(так как  ).
; 
Опыт № 2.
Исследование зависимости
e
=
f
(
E
).
R=120Ом, f=60 кГц, d=0,002м.
 
| U
1
, В
|
U
2
, В
(воздух)
|
U
2
, В
(гетинакс)
|
С
0
, пкФ
|
С,
пкФ
|
Е,
В/м
|
e
|
| 1
|
0,009
|
0,019
|
200
|
420
|
500
|
2,10
|
| 2
|
0,016
|
0,036
|
177
|
398
|
1000
|
2,24
|
| 3
|
0,025
|
0,052
|
184
|
387
|
1500
|
2,09
|
| 4
|
0,031
|
0,070
|
171
|
384
|
2000
|
2,26
|
| 5
|
0,039
|
0,086
|
172
|
380
|
2500
|
2,21
|
График зависимости e = f(E) - приблизительно прямая, так как диэлектрическая проницаемость не зависит от внешнего поля.
Опыт № 3.
Исследование зависимости диэлектрической проницаемости среды от частоты внешнего поля.
U1
= 5В, R=120Ом.
| f
, кГц
|
U
2
, В
(воздух)
|
U
2
, В
(гетинакс)
|
Х
С
, кОм
(гетинакс)
|
С
0
,
пкФ
|
С,
пкФ
|
e
|
| 20
|
0,015
|
0,030
|
20,0
|
199
|
398
|
2,00
|
| 40
|
0,029
|
0,059
|
10,2
|
192
|
391
|
2,04
|
| 60
|
0,041
|
0,089
|
6,7
|
181
|
393
|
2,07
|
| 80
|
0,051
|
0,115
|
5,2
|
169
|
381
|
2,25
|
| 100
|
0,068
|
0,146
|
4,1
|
180
|
387
|
2,15
|
| 120
|
0,078
|
0,171
|
3,5
|
172
|
378
|
2,18
|
| 140
|
0,090
|
0,197
|
3,0
|
181
|
373
|
2,18
|
| 160
|
0,101
|
0,223
|
2,7
|
167
|
370
|
2,21
|
| 180
|
0,115
|
0,254
|
2,4
|
169
|
374
|
2,21
|
| 200
|
0,125
|
0,281
|
2,2
|
166
|
372
|
2,24
|
По графику зависимости e = F(f) видно, что диэлектрическая проницаемость среды не зависит от частоты внешнего поля. График зависимости ХС
=F(1/f) подтверждает, что емкостное сопротивление зависит от 1/f прямо пропорционально.
Опыт № 4.
Исследование зависимости емкости конденсатора от угла перекрытия диэлектрика верхней пластиной.
U1
= 5В, R=120Ом, f=60 кГц, d=0,002м, r=0,06м, n=18.
| a
,
0
|
U
2
,В
|
С,
пкФ
|
С
теор
, пкФ
|
| 0
|
0,039
|
172
|
150
|
| 10
|
0,048
|
212
|
181
|
| 20
|
0,056
|
248
|
212
|
| 30
|
0,063
|
279
|
243
|
| 40
|
0,072
|
318
|
273
|
| 50
|
0,080
|
354
|
304
|
| 60
|
0,089
|
393
|
335
|
Опыт № 5.
Измерение толщины диэлектрической прокладки
.
U1
= 5В, R=120Ом, f=60 кГц.
Схема конденсатора с частичным заполнением диэлектриком.
U2
(стеклотекстолит тонкий)=0,051В,
U2
(стеклотекстолит толстый)=0,093В,
U2
(воздух)=0,039В.
С0
=172пкФ - без диэлектрика;
С1
= 411пкФ - стеклотекстолит толстый;
С1
= 225пкФ - стеклотекстолит тонкий.
;  ;  ;  ;
;  ;  ;
Вывод:
На этой работе мы определили диэлектрическую проницаемость и поляризационные характеристики различных диэлектриков, изучили электрические свойства полей, в них исследовали линейность и дисперсность диэлектрических свойств материалов.
|
