МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

Кафедра радиотехники

Курсовая работа

по курсу: «Общая электротехника и электроника»

«Расчет линейной электрической цепи при гармоническом воздействии.»

Работу выполнил

студент группы ИС-091 Бакаев С.В. подпись

Руководитель доцент Бадаев А.С. подпись

Воронеж 2010

Содержание

1.Техническре задание на курсовую со схемами

2.Выбор варианта схемы

3.Расчёт простой электрической цепи

4.Составление системы уравнений для расчёта токов и напряжений

5.Расчёт токов и напряжений в сложной электрической цепи методом Крамера

6.Расчёт токов и напряжений в сложной электрической цепи методом обращения матрицы

7.Определение достоверности значения токов на основе закона Кирхгофа

8.Определение выражения для комплексного коэффициента передачи

9.Построение графиков АЧХ и ФЧХ с определением их характеристик

1.Техническое задание на курсовую работу со схемами

1. Каждому студенту в соответствии порядковым номером по журналу выбрать вариант схемы по рисунку 1. Различные конфигурации схемы образуются в зависимости от положения ключей « К1 – К5 », которые устанавливаются по номеру варианта, представленному в двоичном коде. Номера позиций единиц и нулей в номере варианта следуют слева направо.

2. Определить величины элементов схемы рисунка 1 и частоту генераторов с помощью следующих формул:

R = 100 · [ 4 + 0,2 ·N ] [Ом]; ( 1 )

С = 100 ·[ 5 + 0,2 ·N ] [Пф]; ( 2 )

Ė_n = 2 [ 7 + (-1)^{n + N} · 0,2 ·N ] ·[В]; ( 3 )

f_n = 10 [ 7 + (-1)^N · 0,2 ·N ] [ кГц] , ( 4 )

где N-номер студента по журналу, а n – номер элемента в схеме.

Рисунок 1 - Схема электрической цепи для выбора своего варианта

3. В схеме, полученной в п. 3.1., исключить (замкнуть) все источники кроме Ė₁ и рассчитать, используя простые преобразования цепей, ток в цепи источника Ė₁ . По результатам расчета построить векторную диаграмму для цепи, в которой все элементы цепи, кроме резистора R, подключенного к источнику ,объединены в эквивалентное сопротивление , как это показано на рисунке 2.

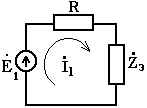
Рисунок 2 – Схема эквивалентной цепи

Осуществить моделирование цепи с помощью программы EWB – 5.12 и определить значение тока в цепи источника Ė₁ , а также напряжения на сопротивлении и R.

4. Используя схему п. 3.1 рассчитать токи и напряжения на её элементах, используя формулы Крамера, а также обращение матриц. Осуществить сравнение результатов.

5. Для схемы из п. 3.3 найти выражение для комплексного коэффициента передачи электрической цепи.

6. Используя формулу для комплексного коэффициента передачи цепи определить выражение для АЧХ и ФЧХ цепи.

7. Построить, используя выражения из п. 3.6, графики для АЧХ и ФЧХ цепи.

8. Определить граничные частоты полосы пропускания и коэффициент прямоугольности цепи, используя результаты п. 3.7.

9. Дать характеристику исследуемой цепи по п. 3.3 с точки зрения фильтрации электрических колебаний.

2.Выбор варианта схемы

Для выбора схемы необходимо представить свой номер по журналу студенческой группы в двоичной форме. Вариант №1 в двоичной форме равен 00001.

Положение ключей в схеме:

Берём данную нам схему для выбора варианта:

Рисунок 2 - Схема электрической цепи для выбора своего варианта

Далее устанавливаем переключатели К1-К5 в положение, соответствующее номеру варианта в двоичной форме. После этого получаем следующую схему:

R R E ₄ C

E ₁ E ₂ E ₃ E ₅

C R R

C

Рисунок3 - Схема цепи для варианта №1

Величины элементов схемы определим по формулам:

R = 100 · [ 4 + 0,2 ·N ] [Ом]

С = 100 ·[ 5 + 0,2 ·N ] [Пф]

Ė_n = 2 [ 7 + (-1)^{n + N} · 0,2 ·N ] ·[В]

f_n = 10 [ 7 + (-1)^N · 0,2 ·N ] [ кГц]

R=100*[4+0,2*1]=420[Ом]

C=100*[5+0,2*1]=520[Пф]

E₁ =E₃ =E₅ =2*[7+0,2*1]*e^{j (25+0,2*1)} =14,4*e^{j *25,2} =13,0295+j*6,1312 [В]

E₂ =E₄ =2*[7-0,2*1]*e^{j (-(25+0,2*1))} =13,6*e^{j (-25,2)} =12,3056-j*5,7906 [В]

f₁ =f₂ =f₃ =f₄ =f₅ =10*[7-0,2*1]=68 [кГц]

3.Расчёт простой электрической цепи

Необходимо определить ток в цепи источника E_1, когда все остальные источники закорочены:

R R C

E ₁

C R R

C

Рисунок4 – Схема простой электрической цепи

Для этого воспользуемся формулами для последовательного и параллельного соединения элементов и вычислим эквивалентное комплексное сопротивление z_э . Значение тока в цепи определим по формуле: İ=Ė/z₀ =Ie^jφ и выразим во временной форме, т. е.: i(t)=I_m cos(ωt+φ)

Получили следующие значения:

x_c = =4501 [Ом]

z_c = -jx_c = -j*4501 [Ом]

z₁ = R+z_c =420-j*4501 [Ом]

z₂ =z₁ *(R+z_c )/(z₁ +R+z_c )=210-j*2251 [Ом]

z₃ =z₂ +R=630-j*2251 [Ом]

z₄ =z₃ * z_c /z₃₊ z_c =324,877-j*1512 [Ом]

z_э =z₄ +R=744,877-j*1512 [Ом]

İ=E₁ /z_э = 1.531*10^-4 +j*8.542*10^-3 [A]

|İ|= 8,543*10^-3 [A]

I_m =|İ|*2^1/2 = 0,012 [A]

i(t)= 0,012*cos(427040t+88,97) [A]

U_R =I*R=3,57*e^j*88,97 [B]

U_{Z э} =I*Z_э =14,3*e ^j*25,2 [B]

Построим векторную диаграмму:

4.Составление системы уравнений для расчёта токов и напряжений

R R E₄ C

E₁ E₂ E₃ E₅

C R R

C

Рисунок 6 – схема сложной электрической цепи

Составим граф электрической схемы, чтобы выбрать независимые контуры и зададим контурные токи:

I₁ I₂ I₃

Рисунок 7 – Граф электрической цепи

Для данных контуров составим систему уравнений по второму закону Кирхгофа с учётом совместного влияния одного контура на другой. Направления обхода во всех контурах выбираются одинаковыми.

I_1* (R+1/(j2πfC))-I₂ *1/(j2πfC)=E₁ -E₂

I₂ *(2R+2/(j2πfC))-I₁ *1/(jπfC)-I₃ *(R+1/(j2πfC))=E₂ -E₃

I₃ *(2R+2/(j2πfC))-I₂ *(R+1/(j2πfC))=E₃ +E₄ -E₅

5.Расчёт токов и напряжений в сложной электрической цепи методом Крамера

Для расчёта электрической схемы составим систему уравнений по методу контурных токов:

I_1* (R+1/(j2πfC))-I₂ *1/(j2πfC)=E₁ -E₂

I₂ *(2R+2/(j2πfC))-I₁ *1/(j2πfC)-I₃ *(R+1/(j2πfC))=E₂ -E₃

I₃ *(2R+2/(j2πfC))-I₂ *(R+1/(j2πfC))=E₃ +E₄ -E₅

По системе уравнений составим матрицу сопротивлений Z, т. е. впишем соответствующие коэффициенты при токах I₁ , I₂ , I₃ :

R+1/(j2πfC) -1/(j2πfC) 0

-1/(j2πfC) 2R+2/(j2πfC) -R-1/(j2πfC)

0 -R-1/(j2πfC) 2R+2/(j2πfC)

Токи в контурах определим по формуле Крамера: İ_n =D_n /D (n=1,2,3….), где D – главный определитель матрицы сопротивлений Z, а D_n – определитель, полученный из D при замене элементов его k-го столбца соответствующими правыми частями уравнений. Правая часть уравнений – матрица-столбец, составленная из свободных членов:

E₁ -E₂ 0,724+j11,992

E= E₂ -E₃ = -0,724-j11,992

E₃ +E₄ -E₅ 12.3056-j5,7906

Главный определитель матрицы равен:

R+1/(j2πfC) -1/(j2πfC) 0

D= -1/(j2πfC) 2R+2/(j2πfC) -R-1/(j2πfC) =

-5,934*10¹⁰ +j*8,404*10¹⁰ [A]

0 -R-1/(j2πfC) 2R+2/(j2πfC)

Найдём определители D₁ ,D₂ ,D₃ :

E₁ -E₂ -1/(j2πfC) 0

D₁ = E₂ -E₃ 2R+2/(j2πfC) -R-1/(j2πfC) = -1.844*10⁸ -j*1.466*10⁸ [A]

E₄ -R-1/(j2πfC) 2R+2/(j2πfC)

R+1/(j2πfC) E₁ -E₂ 0

D₂ = -1/(j2πfC) E₂ -E₃ -R-1/(j2πfC) = -3.144*10⁸ +j*6.83*10⁷ [A]

0 E₄ 2R+2/(j2πfC)

R+1/(j2πfC) -1/(j2πfC) E₁ -E₂

D₃₌ -1/(j2πfC) 2R+2/(j2πfC) E₂ -E₃ = -3.114*10⁸ +j*2.148*10⁷ [A]

0 -R-1/(j2πfC) E₄

Контурные токи будут равны:

I₁ =D₁ /D= -1.302*10^-4 +j*2.286*10^-3 [A]

I₂ =D₂ /D= 2.305*10^-3 +j*2.114*10^-3 [A]

I₃ =D₃ /D= 1.917*10^-3 +j*2.352*10^-3 [A]

6.Расчёт токов и напряжений сложной электрической цепи методом обращения матрицы

Для расчёта токов методом контурных токов, необходимо составить систему уравнений. Воспользуемся системой уравнений, составленной в предыдущем пункте:

I_1* (R+1/(j2πfC))-I₂ *1/(j2πfC)=E₁ -E₂

I₂ *(2R+2/(j2πfC))-I₁ *1/(j2πfC)-I₃ *(R+1/(j2πfC))=E₂ -E₃

I₃ *(2R+2/(j2πfC))-I₂ *(R+1/(j2πfC))=E₃ +E₄ -E₅

Для нахождения токов I₁ , I₂ , I₃ решим систему уравнений методом обращения матрицы. Ī_n =Z_n ^-1 *Ē_n , где Z_n ^-1 – обратная матрица сопротивлений схемы, которая равна:

2,477*10^-4 +j*5,42*10^-4 1,971*10^-4 +j*3,429*10^-4 9,857*10^-5 +j*1,715*10^-4

1,971*10^-4 +j*3,429*10^-4 1,651*10^-4 +j*3,613*10^-4 8,257*10^-5 +j*1,807*10^-4

9,857*10^-5 +j*1,715*10^-4 8,257*10^-5 +j*1,807*10^-4 5,156*10^-5 +j*2,005*10^-4

E₁ -E₂ 0,724+j11,992

E= E₂ -E₃ = -0,724-j11,992

E₃ +E₄ -E₅ 12,3056+j5,7906

2.477*10^-4 +j*5.42*10^-4 1,971*10^-4 +j*3,429*10^-4 9,857*10^-5 +j*1,715*10^-4 0,724+j11,992

I_n = 1,971*10^-4 +j*3,429*10^-4 1,651*10^-4 +j*3,613*10^-4 8,257*10^-5 +j*1,807*10^-4 * -0,724-j11,992 =

9,857*10^-5 +j*1,715*10^-4 8,257*10^-5 +j*1,807*10^-4 5,156*10^-5 +j*2,005*10^-4 12,3056+j5,7906

1.302*10^-4 +j*2.286*10^-3 I₁ = 1.302*10^-4 +j*2.286*10^-3 [A]

= 2.305*10^-3 +j*2.114*10^-3 => I₂ = 2.305*10^-3 +j*2.114*10^-3 [A]

1.917*10^-3 +j*2.352*10^-3 I₃ = 1.917*10^-3 +j*2.352*10^-3 [A]

7.Определение достоверности значения токов на основе закона Кирхгофа

R R E₄ C

E₁ E₂ E₃ E₅

C R R

C

Рисунок 8 - Схема сложной электрической цепи

Рассчитаем токи, проходящие через элементы цепи:

I_R1 =I₁

I_R2 =I₂

I_C1 =I₂ -I₁

I_R3 =I_C2 =I₃ -I₂

I_C3 =I₃ =I_R4

I_R1 +I_C1 -I_R2 = I₁ +(I₂ -I₁ )-I₂ =1.302*10^-4 +j*2.286*10^-3 + (2.305*10^-3 +j*2.114*10^-3 -1.302*10^-4 +j*2.286*10^-3 )-

-2.305*10^-3 +j*2.114*10^-3 =0

8.Определение выражения для комплексного коэффициента передачи

Комплексный коэффициент передачи найдём следующим образом:

K=U_вых /U_вх =U_вых /E₁ , при этом схеме считать R=1000Ом, а С=1 nФ=1*10^-9 Ф.

U_вых – найдём, используя метод контурных токов:

R R C

E ₁

C R R

C

Рисунок 9 – Схема простой электрической цепи для расчёта комплексного коэффициента передачи.

I_1* (R+1/(j2πfC))-I₂ *1/(j2πfC)=E₁

I₂ *(2R+2/(j2πfC))-I₁ *1/(j2πfC)-I₃ *(R+1/(j2πfC))=0

I₃ *(2R+2/(j2πfC))-I₂ *(R+1/(j2πfC))=0

Выразим из (1) ток I₁ . Получим:

I₁ = (E₁ +I₂ Z_c ) / R+Z_c

Полученное выражение подставим во (2) вместо I₁ и выразим ток I₂ . Получим:

I₂ (2R+2Z_c ) – ((E₁ +I₂ Z_c )Z_c / R+Z_c ) – I₃ (R+Z_c ) = 0

I₂ (2R+2Z_c ) (R+Z_c ) – (E₁ Z_c +I₂ Z_c ² ) - I₃ (R+Z_c )² = 0

I₂ (2R+2Z_c ) (R+Z_c ) – E₁ Z_c - I₂ Z_c ² - I₃ (R+Z_c )² = 0

I₂ ((2R+2Z_c ) (R+Z_c ) – Z_c ² ) = E₁ Z_c +I₃ (R+Z_c )²

I₂ = (E₁ Z_c +I₃ (R+Z_c )² ) / ((2R+2Z_c )(R+Z_c )-Z_c ² )

Отсюданаходим I₃ :

I₃ (2R+2Z_c ) – (E₁ Z_c +I₃ (R+Z_c )² )(R+Z_c ) / ((2R+2Z_c )(R+Z_c ) – Z_c ² ) = 0

I₃ (4R³ +12R² Z_c +10RZ_c ² +2Z_c ³ ) - E₁ Z_c R - E₁ Z_c ² – I₃ (R+Z_c )³ = 0

I₃ (4R³ +12R² Z_c +10RZ_c ² +2Z_c ³ - (R+Z_c )³ ) = E₁ Z_c R+E₁ Z_c ²

I₃ (4R³ +12R² Z_c +10RZ_c ² +2Z_c ³ - R³ - 3R² Z_c - 3 RZ_c ² - Z_c ³ ) = E₁ Z_c (R+Z_c )

I₃ (3R³ + 9R² Z_c +7 RZ_c ² + Z_c ³ ) = E₁ Z_c (R+Z_c )

I₃ = E₁ Z_c (R+Z_c ) / (3R³ +9R² Z_c +7RZ_c ² +Z_c ³ )

U_вых = E₁ Z_c (R+Z_c )R / (3R³ +9R² Z_c +7RZ_c ² +Z_c ³ )

K= U_вых /E₁ = Z_c (R+Z_c )R / (3R³ +9R² Z_c +7RZ_c ² +Z_c ³ )

K(f)= 1/(j2πfC) (R+1/(j2πfC))R / (3R³ +9R² 1/(j2πfC)+7R1/(j2πfC)² +1/(j2πfC)³ )

9.Построение графиков АЧХ и ФЧХ с определением их характеристик

Для построения графика АЧХ необходимо вычислить модуль комплексного коэффициента передачи.

j=

R=1000 Ом

C=10^-9 Ф

f=0,100.. 4000000

K(f)= 1/(j2πfC) (R+1/(j2πfC))R / (3R³ +9R² 1/(j2πfC)+7R1/(j2πfC)² +1/(j2πfC)³ )

Для этого воспользуемся соответствующими операциями из программы MathCAD:

x=0,16*0,707

x1=0,16*0,1

Рисунок 10 – График АЧХ цепи

Цепь является полосовым фильтром.

П_0,707 = 50000 – 45000 = 5000 Гц

П_0,1 = 5800 Гц

К_п = П_0,707 / П_0,1 = 0,8

Рисунок 11 – График ФЧХ цепи

Список используемой литературы

1. Попов В.П. Основы теории цепей.-М.:Высшая школа,1985.-420с.

2. Дьяконов В. Mathcad 8/2000: специальный справочник СПб, Питер 2001.-529с.