Задача 1
Фирма осуществляет производство и продажу товара через сеть фирменных магазинов. Данные о цене товара и объеме проданных товаров в среднем за сутки, в одном из географических сегментов рынка приведены в таблице 1.
Таблица 1 Данные о цене и объеме проданных товаров в среднем за сутки
| Цена товара, тыс. руб. |
Объем продажи товара в среднем за сутки |
| 3,00 |
42 |
| 3,05 |
44 |
| 3,10 |
40 |
| 3,15 |
36 |
| 3,20 |
32 |
| 3,25 |
27 |
| 3,30 |
28 |
| 3,35 |
23 |
| 3,40 |
21 |
| 3,45 |
18 |
| 3,50 |
16 |
Необходимо:
1. Проанализировать существующую зависимость между объемом продажи товара и уровнем его цены.
2. Определить коэффициент эластичности между ценой и объемом продажи товара.
3. Определить тесноту связи между ценой и объемом продажи товара.
Решение
Обозначим: «Х» - цена товара, «У» - объем продаж
Представим зависимость графически на рис.1.1

Рис 1.1 – Зависимость объема продажот цены
Произведем сглаживосние по прямой, т.е. построим зависимость У=а+вХ
Применим метод наименьших квадратов и получим зависимость
 , ,
 . .
Решив эту систему, получим такие значения параметров
 , ,
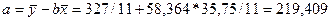 . .
Получается зависимость У=-58,364Х +219,409 или
Q
= 219,409 -58,364 Ц
Таблица 1.2 - Расчетная
| Цена товара, тыс. руб. Х |
Объем продажи товара в среднем за сутки, У |
Х*У |
Х2 |
У2
|
у(х) |
| 3 |
42 |
126 |
9 |
1764 |
44,32 |
| 3,05 |
44 |
134,2 |
9,3025 |
1936 |
41,40 |
| 3,1 |
40 |
124 |
9,61 |
1600 |
38,48 |
| 3,15 |
36 |
113,4 |
9,9225 |
1296 |
35,56 |
| 3,2 |
32 |
102,4 |
10,24 |
1024 |
32,64 |
| 3,25 |
27 |
87,75 |
10,5625 |
729 |
29,73 |
| 3,3 |
28 |
92,4 |
10,89 |
784 |
26,81 |
| 3,35 |
23 |
77,05 |
11,2225 |
529 |
23,89 |
| 3,4 |
21 |
71,4 |
11,56 |
441 |
20,97 |
| 3,45 |
18 |
62,1 |
11,9025 |
324 |
18,05 |
| 3,5 |
16 |
56 |
12,25 |
256 |
15,14 |
| Сумма 35,75
|
327
|
1046,7
|
116,4625
|
10683
|
326,99
|
| Средняя 3,25 |
29,7273 |
95,1545 |
10,5875 |
971,1818 |
29,7260 |
\
Рис 1.2- Линия тренда
2. Коэффициент эластичности рассчитывается по формуле:
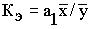
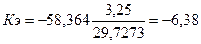
Это число показывает процент изменения объема продаж при изменении цены на 1%.Таким образом, при увеличении цены на 1% объем продаж, в нашем случае, уменьшался на 6,38%.
Теснота связи между показателями цены и объема продаж рассчитывается по формуле:
 (1.4) (1.4)
Если r = 0 – 0,3 –
связь слабая
r = 0,3 – 0,5 –
связь умеренная
r = 0,5 – 0,7 –
связь заметная
r = 0,7 – 0,98 –
связь сильная
r >0,98 –
стремится к функциональной
r > 0 –
связь прямая
r< 0 –
связь обратная
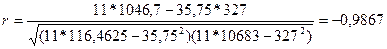
Так как значение r
близко к 1, следовательно, связь между ценой и объемом продажи сильная.
В заключение можно сделать вывод:
1. Спрос эластичен. Коэффициент эластичности по абсолютному значению больше единицы и равен 6,38.
2. Между ценой и объемом производства существует обратная связь, которая стремится к функциональной
Задача 2
Для оперативного регулирования цены с учетом установленной эластичности спроса проанализировать затраты на производство и обращение товара на основании следующих исходных данных.
Таблица 2.1 Исходные данные об объеме производства и суммарных затратах на производство товара в среднем за сутки
| Месяц |
Расходы производства в среднем за сутки, тыс.руб. ТС |
Объем реализации в среднем за сутки, штук, Q |
| 01 |
2480 |
220 |
| 02 |
2385 |
170 |
| 03 |
2430 |
210 |
| 04 |
2400 |
190 |
| 05 |
2360 |
170 |
| 06 |
2370 |
160 |
| 07 |
2500 |
240 |
| 08 |
2550 |
260 |
| 09 |
2535 |
250 |
| 10 |
2600 |
270 |
| 11 |
2615 |
280 |
| 12 |
2460 |
200 |
Таблица 2.2. Исходные данные об объеме реализации и суммарных затратах обращения в среднем за сутки
| Месяц |
Затраты обращения в среднем за сутки, тыс.руб. |
Объем реализации в среднем за сутки, штук, Q |
| 01 |
1155 |
190 |
| 02 |
1135 |
160 |
| 03 |
1145 |
180 |
| 04 |
1190 |
230 |
| 05 |
1140 |
180 |
| 06 |
1200 |
240 |
| 07 |
1300 |
260 |
| 08 |
1225 |
250 |
| 09 |
1300 |
270 |
| 10 |
1195 |
230 |
| 11 |
1230 |
280 |
| 12 |
1220 |
260 |
Необходимо:
1. Используя данные таблицы 2.1 разделить суммарные издержки производства на постоянные и переменные затраты используя метод "максимальной и минимальной точки".
2. Используя данные таблицы 2.2 разделить суммарные издержки обращения товара на постоянные и переменные затраты с помощью метода наименьших квадратов.
3. Составить математическую модель валовых издержек производства и обращения товара.
Решение
Из всей совокупности данных выбираются два периода с наименьшим и наибольшим объемом производства. Из таблицы 2.1 видно, что наибольший объем производства в декабре составил 280 штук. Наименьший объем производства в августе - он составил 160штук.
Для расчета постоянных и переменных затрат составляем вспомогательную таблицу 2.3.
Таблица 2.3 Вспомогательная таблица для расчета постоянных и переменных затрат
| Показатель |
Объем производства |
Разность между максимальными и минимальными величинами |
| максимальный |
минимальный |
1.Уровень производства в среднем за сутки, (Q)
2. Q%
|
280
100%
|
160
57,14 %
|
120
42,86 %
|
| 3. Расходы производства в среднем за сутки, тыс. руб. (ТС) |
2615
|
2370
|
245
|
Определим ставку переменных издержек (удельные переменные расходы в себестоимости единицы продукции) по следующей формуле (2.1)
VC’= (ΔTCx100/ΔQ%)/Qmax
(2.1)
где VC ' – ставка удельных переменных издержек;
ΔТС - разность между максимальными и минимальными величинами, равная 245тыс. рублей;
ΔQ % - разность между максимальными и минимальными величинами, равная 42,86%;
Q max- максимальный объем производства в среднем за сутки, равный 280 штук.
VC ' = (245 х 100 / 42,86 )/280 = 2,04 тыс. руб./ шт.
Общая сумма постоянных издержек (FC) определяется по следующей формуле (2.2):
FC = TСmax
- VC' *Qmax
(2.2)
где TCmax
-
суммарные издержки, соответствующие максимальному уровню производства, равные 2615 тыс. руб.
FC
= 2615-2,04*280=2044 тыс. руб.
Таким образом, получена математическая модель суммарных издержек производства (ТС), которые могут быть рассчитаны по формуле (2.3).
ТС=FС+ VC' * Q = 2044 +2,04 * Q (2.3)
где Q -
объем производства товара, штук.
Полученную математическую модель суммарных издержек производства проверяем на соответствие ее фактическим значениям (ходя бы по данным одного месяца). Так в январе месяце теоретическое значение ТС, рассчитанное с помощью формулы (2.3), получается равное
ТС=2044+2,04*220=2492,8 тыс. рублей, а фактическое значение в январе равно 2480 тыс. рублей, то есть значения близки. Поэтому модель, полученную по формуле 2.3, можно использовать в практической деятельности.
Таким образом, выражение 2.3 позволяет сделать вывод, что в среднем за сутки суммарные постоянные издержки производства товаров составляли 2-44 тысяч рублей, а остальные – переменные издержки. Так, в январе суммарные переменные издержки составляли 2,04*220= 448,8 тысяч рублей.
2.
Согласно этому методу модель суммарных затрат представляет собой уравнение прямой линии, то есть для нахождения постоянных и переменных издержек необходимо рассчитать коэффициенты a и b в уравнении прямой линии:
у = a + b*x,
где y – суммарные издержки обращения;
a – сумма постоянных издержек обращения;
b –
удельные переменные издержки обращения в расчет на единицу товара;
x -
объем реализации, штук.
Определим средние значения показателей:
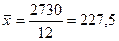 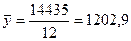
Удельные переменные издержки определяются по формуле (2.4)

 получаем VC '=1,221 получаем VC '=1,221
Для их расчета величины составляем вспомогательную таблицу 2.4.
Таблица 2.4 Вспомогательная таблица для расчета величины b
| Месяц |
Объем реализации (x) |
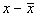 |
Суммарные издержки (y) |
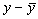 |
(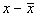 )2 )2
|
(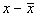 )*( )*(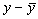 ) ) |
| 01 |
190 |
-37,5 |
1155 |
-47,9 |
1406,25 |
1796,25 |
| 02 |
160 |
-67,5 |
1135 |
-67,9 |
4556,25 |
4583,25 |
| 03 |
180 |
-47,5 |
1145 |
-57,9 |
2256,25 |
2750,25 |
| 04 |
230 |
2,5 |
1190 |
-12,9 |
6,25 |
-32,25 |
| 05 |
180 |
-47,5 |
1140 |
-62,9 |
2256,25 |
2987,75 |
| 06 |
240 |
12,5 |
1200 |
-2,9 |
156,25 |
-36,25 |
| 07 |
260 |
32,5 |
1300 |
97,1 |
1056,25 |
3155,75 |
| 08 |
250 |
22,5 |
1225 |
22,1 |
506,25 |
497,25 |
| 09 |
270 |
42,5 |
1300 |
97,1 |
1806,25 |
4126,75 |
| 10 |
230 |
2,5 |
1195 |
-7,9 |
6,25 |
-19,75 |
| 11 |
280 |
52,5 |
1230 |
27,1 |
2756,25 |
1422,75 |
| 12 |
260 |
32,5 |
1220 |
17,1 |
1056,25 |
555,75 |
| итого |
2730
|
14435
|
17825
|
21787,5
|
| среднее |
227,5
|
1202,9167
|
Тогда суммарные переменные издержки на среднесуточный объем продаж (VC) составят:
VC = Q*VC' = 227,5*1,221 =277,6904тыс. рублей.
Сумма постоянных издержек (FС) рассчитывается по средним значениям таблицы 2.4 и
составляют:
FC = TC - VC
= 1202,9167- 277,6904= 925,226тыс. рублей.
Таким образом, суммарные издержки обращения могут быть рассчитаны по формуле:
ТС= 925,226+1,221 Q, (2.5)
где Q - объем реализации товаров в среднем за сутки, штук.
Полученное выражение (2.5) является математической моделью суммарных издержек обращения товаров, которую необходимо проверить на ее соответствие фактическим данным. Проверку осуществляем по любому месяцу, например январю.
Подставляем в выражение (2.5) объем продаж января месяца, равный 190 штук и получаем суммарные издержки обращения, равные:
ТС=925,226+1,221*190=1157,216 тыс. рублей, что соответствует фактическим данным, приведенным в таблице 2.6., которые равны 1155 тыс. руб.
Таким образом, выражение (2.5) позволяет сделать вывод, что постоянные издержки обращения составляют 925,226 (т.к. они в выражении являются постоянной величиной) тыс. рублей. Переменные затраты на единицу изделия составляют 1,221 тыс.руб. или на весь объем реализации в январе 231,99тыс. руб.
3.Используя результаты, полученные в пунктах 1 и 2 задачи, составляем математическую модель валовых издержек производства и обращения товаров. Эта модель должна объединить две ранее полученные модели. Для этого определяем сумму постоянных издержек производства и реализации товаров, которая в нашем случае равна:
2044+925,23=2969,23 тыс. рублей.
Рассчитываем сумму удельных переменных издержек производства и обращения товаров, которая составила:
2,04+1,22=3,26 тыс. руб./шт.
Таким образом, валовые издержки производства и обращения могут быть рассчитаны по формуле:
ТС = 2969,23+3,26Q
Задание к задаче № 3
Используя результаты, полученные в задачах №1 и №2 необходимо определить:
1. Оптимальный уровень цены с учетом достижения максимальной прибыли (валовой маржи), предварительно разработав экономико-математическую модель задачи.
2. Объем производства и продажи, обеспечивающий прибыль равную 50 тыс. рублей в день при складывающихся на рынке ценах.
3. Оптимальный уровень цены, обеспечивающий уровень прибыли, равный 50 тыс. рублей в день при уровне производства и реализации равном 3000 и более штук.
Решение
Используя результаты предыдущих задач:
1 .Полученную зависимость объема реализации от цены (коэффициенты в выражении можно округлить):
Q
= 220 -59 Ц
где Q -
среднесуточная продажа;
Ц - цена единицы товара, тыс. рублей.
2. Математическую модель суммарных издержек производства и обращения:
ТС = 2969,23+3,26Q
Необходимо определить оптимальный уровень цены с учетом достижения максимального значения прибыли (валовой маржи).
1. Для этого необходимо разработать экономико-математическую модель задачи (формула прибыли):
П = Д - ТС =Q*Ц -VC'*Q - FC= Mв - FC (3.1)
где Мв
- валовая маржа (разность между доходами и суммарными переменными издержками)
Подставляем в формулу (3.1) соответствующие значения Q ,VC' и FC .
Тогда формула преобразуется:
П=Ц(220-59Ц) – 3,26 (220-59Ц) -FC = 220Ц - 59Ц2
– 717,2+192,34Ц - F C=
412,34 Ц- 59Ц2
-717,2 -2969,23 =412,34 Ц- 59Ц2
-3686,43 (3,2)
Оптимальная цена соответствует той, где производная прибыли по цене равна нулю. Для расчета оптимальной цены возьмем производную итогового выражения (3.2) по цене и приравняем к нулю:

Тогда оптимальная цена равна:
Ц опт = 412,34/118=3,5 тыс. руб.
Для проверки результата проведем дополнительные расчеты в таблице 3.1. Для упрощения расчетов в формуле (3.2) не учитываем значение FC=
2969,23, которое не влияет на конечный результат.
Таблица. 3.1- расчетная
| Цена |
412,34Ц |
Ц2
|
59Ц2
|
412,34Ц-59Ц |
Валовая маржа = 412,34-59Ц-717,2 тыс. руб. |
| 3 |
1237,02 |
9 |
531 |
706,02 |
-11,18 |
| 3,05 |
1257,637 |
9,3 |
548,7 |
708,937 |
-8,263 |
| 3,1 |
1278,254 |
9,6 |
566,4 |
711,854 |
-5,346 |
| 3,15 |
1298,871 |
9,9 |
584,1 |
714,771 |
-2,429 |
| 3,2 |
1319,488 |
10,2 |
601,8 |
717,688 |
0,488 |
| 3,25 |
1340,105 |
10,5 |
619,5 |
720,605 |
3,405 |
| 3,3 |
1360,722 |
10,8 |
637,2 |
723,522 |
6,322 |
| 3,35 |
1381,339 |
11,2 |
660,8 |
720,539 |
3,339 |
| 3,4 |
1401,956 |
11,5 |
678,5 |
723,456 |
6,256 |
| 3,45 |
1422,573 |
11,9 |
702,1 |
720,473 |
3,273 |
| 3,5
|
1443,19
|
12,2
|
719,8
|
723,39
|
6,19
|
Из расчетов по табл. 3.1 видно, что максимальная валовая маржа имеет свое значение 6,19 тыс. руб при цене 3,5 тыс.руб.
2. Предположим, что необходимо определить количество товара, который нужно продать, чтобы получить целевую прибыль равную 50 тыс. рублей в день. Используя исходные данные задачи 3 и формулу (3.1), определим:
П = Q*Ц - FC - VC ' * Q=100тыc.pyб.
Тогда: Q=
(50 + 2969,23): Ц - VC'=
3019,23/(Ц – 3,26)
Расчеты объемов производства приведены в таблице 3.2.
Таблица 3.2 Расчеты для определения объема продаж
| Цена единицы товара, тыс. руб. |
Ц – 3,26 |
Среднесуточная продажа товара, шт. |
| 3,3 |
0,04 |
75481 |
| 3,4 |
0,14 |
21566 |
| 3,5
|
0,24
|
12580
|
| 3,6 |
0,34 |
8880 |
| 3,7 |
0,44 |
6862 |
| 3,8 |
0,54 |
5591 |
Таким образом, для получения прибыли в день 50 тыс. рублей по рассчитанной ранее оптимальной цене 3,5 тыс. руб. необходимо продать 12580 штук.
3. Оптимальный уровень цены, обеспечивающий уровень прибыли, равный 50 тыс. рублей в день при уровне производства и реализации равном 3000 и более штук.
Используя исходные данные задачи 3 и формулу (3.1) определяем:
Q Ц - FC - VC'*Q = 100
Ц = (50+FC+VC'*Q): Q =(50+2969,23+3,26 Q):
Q=(3019,23+3,26Q):Q
Расчеты среднего уровня цены приведены в таблице 3.3.
Таблица 3.3 Расчеты для определения среднего уровня цены
Среднесуточная
продажа (Q )
|
Уровень цены (Ц) |
| 3000 |
4,27 |
| 3450 |
4,13 |
Для производственных возможностях 3000 шт.в день средняя цена составляет 4,27 тыс. руб. Для увеличения производства на 15%, средняя цена упадет на 3,28% и составит 4,13 тыс.руб. Это вполне выгодное предложение так как снижение цена на 3,28% приведет к росту объема продаж на 15%. А из-за роста оборота вырастит прибыль на (100-3,28)*1,15=111,23% или на 11,23%
Список использованной литературы
1. Багиев Г. Л. Основы современного маркетинга. - С.П.Б.:2000 ,.
2. Дойль П. Менеджмент: стратегия и практика. – СПб.: ПИТЕР, 2001
3. Классика маркетинга / Сост. Б. М. Энис, К. Т. Кокс., Москва М.П. — СПб.: Питер, 2001.
4. Кемпбелл А., Стоунхаус Дж. Стратегический маркетинг и менеджмент. – М.: ООО «Издательство Проспект», 2003, - 336 с.
5. Крылова Г. Д. Практикум по маркетингу. - М.: ЮНИТИ 2000.
6. Люкшинов А.Н. Стратегический маркетинг и менеджмент: Уч. пособ. Для вузов. – М.: ЮНИТЛ, 2001, - 375 с.
7. Минцберт Г., Альстрэнд Б. Школы стратегий / СПб: Издательство «Питер», 2000 – 336 с.
|