МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Кафедра прикладной математики
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Информатика»
2007
Задания к контрольной работе
Задача №1
Выполнить расчеты с использованием финансовых функций. Оформить таблицу и построить диаграмму, отражающую динамику роста вклада по годам. Описать используемые формулы, представить распечатку со значениями и с формулами:
15.1
Вклад размером 500 тыс. грн. положен под 12% годовых. Рассчитайте, какая сумма будет на сберегательном счете через шесть лет, если проценты начисляются каждые полгода
15.2
Определить текущую стоимость обычных ежегодных платежей размером 20 тыс. грн. в течение трех лет при начислении 16% годовых.
Задача №2
Произвести экономический анализ для заданных статистических данных и сделать вывод.
Таблица 1 – Статистические данные
| X |
1,01 |
1,51 |
2,02 |
2,51 |
3,01 |
3,49 |
3,98 |
4,48 |
4,99 |
5,49 |
| Y |
5,02 |
5,92 |
7,14 |
8,32 |
9,02 |
9,58 |
11,06 |
11,96 |
12,78 |
13,98 |
Задача №3
Связь между тремя отраслями представлена матрицей прямых затрат А. Спрос (конечный продукт) задан вектором
 . Найти валовой выпуск продукции отраслей . Найти валовой выпуск продукции отраслей
 . Описать используемые формулы, представить распечатку со значениями и с формулами. . Описать используемые формулы, представить распечатку со значениями и с формулами.
 
Задача №4
Решить задачу линейного программирования.
Вариант 15
Коммерческий магазин хочет закупить овощи А и В. Количество овощей, закупочные цены и цены, по которым магазин продает овощи, приведены в таблице 8.
Таблица 8
| Овощи |
Цены |
Количество овощей |
| Закупка |
Реализация |
| А |
1,6 |
2,4 |
60 |
| В |
1,7 |
2,2 |
70 |
Как выгоднее вложить деньги, если общая сумма, которой располагается магазин в данное время, составляет 180 д.е., причем овощей А нужно приобрести не менее 10 тонн.
Задача №1
15.1
Вклад размером 500 тыс.грн. положен под 12% годовых. Рассчитайте, какая сумма будет на сберегательном счете через шесть лет, если проценты начисляются каждые полгода
Решение
Для расчета текущей стоимости вклада будем использовать функцию
БЗ (норма; число_периодов; выплата; нз; тип),
где норма
– процентная ставка за один период. В нашем случае
величина нормы составляет 13% годовых.
число периодов
– общее число периодов выплат. В нашем случае
данная величина составляет 6 лет.
выплата
– выплата, производимая в каждый период. В нашем
случае данная величина полагается равной -100000.
нз
– текущая стоимость вклада. Равна 0.
тип
– данный аргумент можно опустить (равен 0).
Получим следующее выражение БЗ (12/2; 12; 0; – 500; 0) = 1006.10 тыс. грн.
Расчет будущей стоимости вклада по годам приведен в таблице 3.
Таблица 3 – Расчет будущего вклада
| РАСЧЕТ ТЕКУЩЕГО ВКЛАДА
|
| ГОД
|
СТАВКА
|
ЧИСЛО
|
ВЫПЛАТА
|
ВКЛАД, тыс. грн
|
ТИП
|
ВЕЛИЧИНА
|
| (ГОД)
|
ПЕРИОДОВ
|
ВКЛАДА, тыс. грн
|
| 1 |
12% |
2 |
0 |
-500 |
0 |
561.80 |
| 2 |
12% |
4 |
0 |
-500 |
0 |
631.24 |
| 3 |
12% |
6 |
0 |
-500 |
0 |
709.26 |
| 4 |
12% |
8 |
0 |
-500 |
0 |
796.92 |
| 5 |
12% |
10 |
0 |
-500 |
0 |
895.42 |
| 6 |
12% |
12 |
0 |
-500 |
0 |
1006.10 |
Гистограмма, отражающая динамику роста вклада по годам представлена ниже.
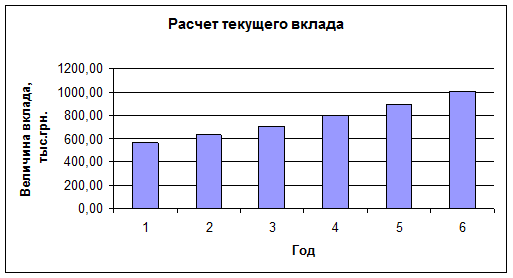
Рисунок 1 – Динамика роста вклада по годам
Вывод:
Расчеты показывают, что на счете через шесть лет будет 1006.10 тыс. грн.
15.2
Определить текущую стоимость обычных ежегодных платежей размером 20 тыс. грн. в течение трех лет при начислении 16% годовых.
Решение
Для расчета используем функцию
ПЗ (норма; Кпер; выплата; бс; тип),
где норма
= 16% – процентная ставка за один период;
Кпер
= 3 – общее число периодов выплат;
выплата
= 20 тыс. грн. – Ежегодные платежи;
При этом:
ПЗ (16%; 3; 20) = – 44,92 тыс. грн.
Результат получился отрицательный, поскольку это сумма, которую необходимо вложить.
Вывод:
Таким образом при заданных условиях текущая стоимость вклада составляет 44,92 тыс. грн.
Задача №2
1.2.
Произвести экономический анализ для заданных статистических данных и сделать вывод.
Таблица 4 – Заданные статистические данные
| X |
1,01 |
1,51 |
2,02 |
2,51 |
3,01 |
3,49 |
3,98 |
4,48 |
4,99 |
5,49 |
| Y |
5,02 |
5,92 |
7,14 |
8,32 |
9,02 |
9,58 |
11,06 |
11,96 |
12,78 |
13,98 |
Решение
1. Вводим значения X и Y, оформляя таблицу;
2. По данным таблицы строим точечную диаграмму (см. рисунок 2);
3. Выполнив пункты меню Диаграмма – Добавить линию тренда, получаем линию тренда (см. рисунок 2);
Из возможных вариантов типа диаграммы (линейная, логарифмическая, полиномиальная, степенная, экспоненциальная), выбираем линейную зависимость, т. к. она обеспечивает наименьшее отклонение от заданных значений параметра Y.
y = 1.9733
x + 3.0667
– уравнение зависимости;
R2
= 0.9962
– величина достоверности аппроксимации;
4. Для обоснования сделанного выбора оформим таблицу 5 – сравнительный анализ принятых и заданных значений параметра Y.
В этой таблице:
Y1
– значение параметра Y, согласно принятой гипотезе;
Y–значение параметра Y, согласно заданным данным.
ε – величина арифметического отклонения ε = Y- Y1
;
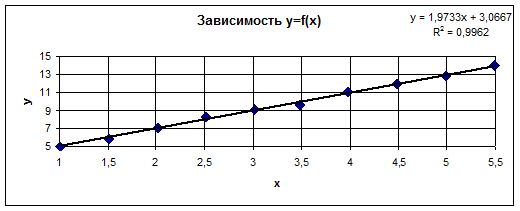
Рисунок 2 – график зависимости у=f(x)
Таблица 5 – Сравнительный анализ заданных и принятых значений Y
| X |
1.01 |
1.51 |
2.02 |
2.51 |
3.01 |
3.49 |
3.98 |
4.48 |
4.99 |
5.49 |
| Y |
5.02 |
5.92 |
7.14 |
8.32 |
9.02 |
9.58 |
11.06 |
11.96 |
12.78 |
13.98 |
| Y1 |
5.06 |
6.05 |
7.05 |
8.02 |
9.01 |
9.95 |
10.92 |
11.91 |
12.91 |
13.90 |
| E |
-0.04 |
-0.13 |
0.09 |
0.30 |
0.01 |
-0.37 |
0.14 |
0.05 |
-0.13 |
0.08 |
Вывод:
На основе собранных статистических данных, представленных в таблице находим экономическую модель – принятая гипотеза имеет степенную зависимость и выражается уравнением
y = 1.9733
x + 3.0667
Экономическое прогнозирование на основе уравнения данной зависимости отличается достоверностью в области начальных значений параметра X– величина ε принимает малые значения и неточностью в долгосрочном периоде – в области конечных значений параметра X.
Задача №3
7.
Связь между тремя отраслями представлена матрицей прямых затрат А. Спрос (конечный продукт) задан вектором X. Найти валовой выпуск продукции отраслей Х. Описать используемые формулы, представить распечатку со значениями и с формулами.
 
Решение
Данная задача связана с определением объема производства каждой из N отраслей, чтобы удовлетворить все потребности в продукции данной отрасли. При этом каждая отрасль выступает и как производитель некоторой продукции и как потребитель своей и произведенной другими отраслями продукции. Задача межотраслевого баланса – отыскание такого вектора валового выпуска X, который при известной матрице прямых затрат обеспечивает заданный вектор конечного продукта Y.
Матричное решение данной задачи:
X
= (
E
-
A
)-1
Y
. [2]
Из существующих в пакете Excel функций для работы с матрицами при решении данной задачи будем использовать следующие:
1. МОБР – нахождение обратной матрицы;
2. МУМНОЖ – умножение матриц;
3. МОПРЕД – нахождение определителя матрицы;
Также при решении данной задачи использовали сочетание клавиш:
F2 CTRL + SHIFT + ENTER – для получения на экране всех значений результата.
Расчетные формулы для решения данной задачи показаны в таблице 7.
Результат решения показан в таблице 6.
Таблица 6 – Расчетные формулы
| Затраты |
Выпуск (потребление) |
Конечный |
Валовый |
| (отрасли) |
отрасль А |
отрасль B |
отрасль C |
продукт |
выпуск |
| отрасль А |
0.05 |
0.1 |
0.4 |
47 |
=МУМНОЖ (F12:H14; E3:E5) |
| отрасль B |
0.1 |
0.1 |
0.3 |
58 |
=МУМНОЖ (F12:H14; E3:E5) |
| отрасль C |
0.3 |
0.15 |
0.2 |
81 |
=МУМНОЖ (F12:H14; E3:E5) |
| Решение |
| Е = |
1 |
0 |
0 |
| 0 |
1 |
0 |
| 0 |
0 |
1 |
| Е-А = |
=B8‑B3 |
=C8‑C3 |
=D8‑D3 |
(Е-А)-1
= |
=МОБР (B12:D14) |
=МОБР (B12:D14) |
=МОБР (B12:D14) |
| =B9‑B4 |
=C9‑C4 |
=D9‑D4 |
=МОБР (B12:D14) |
=МОБР (B12:D14) |
=МОБР (B12:D14) |
| =B10‑B5 |
=C10‑C5 |
=D10‑D5 |
=МОБР (B12:D14) |
=МОБР (B12:D14) |
=МОБР (B12:D14) |
| Det (E-A)= |
=МОПРЕД (B12:D14) |
Таблица 7 – Результат решения
| Затраты |
Выпуск (потребление) |
Конечный |
Валовый |
| (отрасли) |
отрасль А |
отрасль B |
отрасль C |
продукт |
выпуск |
| отрасль А |
0.1 |
0.1 |
0.4 |
47 |
140 |
| отрасль B |
0.1 |
0.1 |
0.3 |
58 |
140 |
| отрасль C |
0.3 |
0.15 |
0.2 |
81 |
180 |
| Решение |
| Е = |
1 |
0 |
0 |
| 0 |
1 |
0 |
| 0 |
0 |
1 |
| Е-А = |
1 |
-0.1 |
-0.4 |
(Е-А)-1
= |
1.322880941 |
0.27438 |
0.76433 |
| -0.1 |
0.9 |
-0.3 |
0.333170015 |
1.25429 |
0.63694 |
| -0.3 |
-0.2 |
0.8 |
0.558549731 |
0.33807 |
1.65605 |
| Det (E-A)= |
0.51025 |
Вывод:
Для удовлетворения спроса на продукцию отрасли А величиной 47 д.е., отрасли В – 58 д.е. и отрасли С – 81 д.е. необходимо произвести продукции отрасли А на сумму 140 д.е., отрасли В на сумму 140 д.е., отрасли С – на сумму 180 д.е.
Задача №4
Вариант 15
Коммерческий магазин хочет закупить овощи А и В. Количество овощей, закупочные цены и цены, по которым магазин продает овощи, приведены в таблице 8.
Таблица 8
| Овощи |
Цены |
Количество овощей |
| Закупка |
Реализация |
| А |
1,6 |
2,4 |
60 |
| В |
1,7 |
2,2 |
70 |
Как выгоднее вложить деньги, если общая сумма, которой располагается магазин в данное время, составляет 180 д.е., причем овощей А нужно приобрести не менее 10 тонн.
Решение
Решение данной задачи состоит из трех основных этапов:
1. составление математической модели (формализация задачи);
Обозначим величину прибыли от овоща А как А, а величину прибыли от обоща В как В, тогда получим, что прибыль от продажи овоща А составляет (2,4–1,6) А, соответственно овоща В – (2,2–1,7) В. Суммарная прибыль магазина от продажи овощей составит (2,4–1,6) А+(2,2–1,7) В=0,8А+0,5В.
Тогда целевая функция имеет вид Z
=0,8А
– 0,5В
суммарная прибыль должна быть наибольшей (максимальной).
Данная задача содержит две неизвестных переменных, т.е. ее можно назвать плоской и она может быть решена графически.
Составим систему ограничений, исходя из условия задачи:
- ограничение на покупку овощей по деньгам:
На покупку овоща А расходуется 1,6 д.е на 1 тонн. На все количество овоща А расходуется 1,6 А д.е. На овощ В расходуется 1,7 д.е. на 1 тонну на закупку овоща В тратят 1,7 В. Значит, исходя из условия задачи, суммарная сумма на которую закупаются овоща не должна превышать 180 д.е. Получим первое неравенство системы:
1,6 А + 1,7 В ≤ 180;
– дополнительные условия:
В условии задачи содержится дополнительное условие – закупка овоща А не менее 10 тонн и не более 60 тонн. т.е. имеем дополнительные неравенства для овоща А:
А ≥ 10;
А ≤ 60;
Для овоща В наложено верхнее ограничение не более 70 тонн, из условия задачи понятно что нижним ограничение является 0. Получаем дополнительные неравенства для овоща В:
В ≥ 0;
В ≤ 70;
Получили математическую модель задачи:
 1,6А + 1,7В ≤ 180; 1,6А + 1,7В ≤ 180;
А
≥ 10; А
≤ 60;
В
≥ 0; В
≤ 70;
2. решение формализованной задачи;
Решив задачу графически и с использованием пакета Excel, получим одинаковое решение:
А = 60 тонн.
В = 49,412 тонн.
Ход решения – см. таблица 9 и рисунок 3
Вывод: Для получения максимальной прибыли в размере 72,7 ден. ед. необходимо следующим образом потратить существующие деньги:
- овощ А закупить в количестве 60 тонн.
- овощ В закупить в количестве 49,412 м.
При этом необходимо потратит все деньги: 180 д.е.
Графическое решение задачи 4
Необходимо найти значения (А, В), при которых функция Z
=0,8 А
– 0,5 В
достигает максимума. При этом А и В должны удовлетворять системе ограничений, приведенной ранее:
 1,6А + 1,7В ≤ 180; 1,6А + 1,7В ≤ 180;
А
≥ 10; А
≤ 60;
В
≥ 0; В
≤ 70;
Решение
1. Строим область, являющуюся пересечением всех полуплоскостей, уравнения которых приведены в системе ограничений. Например, полуплоскость 1,6А + 1,7В ≤ 180;
представляет собой совокупность точек, лежащих ниже прямой, соединяющей точки с координатами (65; 44,705) и (32,813; 75). Аналогично – остальные. Построение – рисунок 3.
2. Находим градиент функции Z.
gradz = {0,8; 0,5}
Строим вектор с началом в точке (0; 0) и концом в точке (0,8; 0,5).
Построение – рисунок 3.
3. Строим прямую, перпендикулярную вектору градиента. Так как по условию мы ищем максимум функции Z, то передвигаем прямую в направлении указанном вектором. Точка максимума – последняя точка области, которую пересечет эта прямая. В нашем случае, искомая точка лежит на пересечении прямых А=60 и 1,6 А + 1,7 В = 180;
Построение – рисунок 3
4. Решаем систему уравнений
 А=60; А=60;
1,6А + 1,7В = 180; В = 49,412;
Т.е графическое построение дало результат (60; 49,412).
Максимальное значение функции Z = 0,8*60+0,5*49,412=72,7.

Рисунок 3 – Графическое решение задачи 4
Решение задачи 4 с использованием пакета
Excel
В пакете Excel решение задачи линейного программирования осуществляется с помощью пункта меню Сервис – Поиск решения.
Распечатка решения задачи в Excel приведена в таблице 9.
Формулы, по которым был произведен расчет, приведены в таб. 10.
Таблица 9 – Решение задачи в Excel
| Переменные |
| A |
B |
| Значения |
60 |
49.412 |
| Нижняя граница |
10 |
0 |
| Верхняя граница |
60 |
70 |
| Z=(2.4–1.6) A+(2.2–1.7) B |
0.8 |
0.5 |
72.706 |
max |
| Коэффициенты целевой функции |
| Коэффициенты |
Значение |
Фактические ресурсы |
Неиспользованные ресурсы |
| Система ограничений |
1.6 |
1.7 |
180 |
<= |
180 |
0 |
Таблица 10 – Формулы для расчета в Excel
Переменные
|
| A |
B |
| Значения |
60 |
49.412 |
| Нижняя граница |
10 |
0 |
| Верхняя граница |
60 |
70 |
| Z=(2.4–1.6) A+(2.2–1.7) B |
0.8 |
0.5 |
=СУММПРОИЗВ
(B3:C3; B6:C6)
|
max |
| Коэффициенты целевой функции |
| Коэффициенты |
Значение |
Фактические ресурсы |
Неиспользо-
ванные ресурсы
|
| Система ограничений |
1.6 |
1.7 |
=СУММПРОИЗВ
(B3:C3; B10:C10)
|
<= |
180 |
=F10‑D10 |
Список используемой литературы
1.Финансово-экономические расчеты в Excel. – 2-е изд., доп. – М: Информационно-издательский дом «Филинъ», 2005. – 184 с.
2.Методический указания и контрольные задания по дисциплине «Информатика» для студентов заочного факультета экономического направления обучения. Ч. 3/ Сост. В.Н. Черномаз, Т.В. Шевцова, О.А. Медведева. – ДГМА, 2006 – 40 стр.
|