Проходження світла через кристали. Нелінійні оптичні явища
Оптичні середовища, показник заломлення яких залежить від напряму поширення світлової хвилі, називають анізотропними або кристалічними.
Анізотропія кристалів зумовлена симетрією їх внутрішнього стану. В ізотропному середовищі при впливі електричного поля  виникає зміщення електричних зарядів, що характеризується вектором електричного зміщення виникає зміщення електричних зарядів, що характеризується вектором електричного зміщення  , причому вектори , причому вектори  і і  колінеарні і пов'язані рівнянням (1). колінеарні і пов'язані рівнянням (1).
В анізотропному середовищі в загальному випадку електричні заряди зміщуються не у напрямі прикладеного електричного поля і вектори не співпадають ні по модулю, ні у напрямі.
Однак в будь-якому кристалі існують три головних напрями, для яких зберігається колінеарність векторів  і і  і справедливі співвідношення: і справедливі співвідношення:
 ; ;  ; ;  , (1) , (1)
причому осі координат  , ,  , ,  вибрані вздовж головних напрямів. У загальному випадку вибрані вздовж головних напрямів. У загальному випадку  (рис. 1. а). (рис. 1. а).

У вибраній системі координат  , ,  , ,  для будь-якого кристала для будь-якого кристала
Рис. 1 Проходження світла через кристали
Головні напрями можна записати рівняння так званої характеристичної поверхні:
 , ,
де  , ,  , ,  - головні показники заломлення. - головні показники заломлення.
Характеристична поверхня являє собою еліпсоїд Френеля, причому довжини головних напівосей цього еліпсоїда рівні відповідно ( ), ( ), ( ) і ( ) і ( ) (рис. 1 б). ) (рис. 1 б).
З аналітичної геометрії відомо, що будь-який еліпсоїд має два кругових перетини.
Напрями, що перпендикулярні круговим перетинам еліпсоїда Френеля, називають оптичними осями кристала. Отже, кристал у загальному випадку має дві оптичні осі (двовісний кристал). Якщо  , то еліпсоїд Френеля вироджується в еліпсоїд обертання, що характеризує одновісний кристал з оптичною віссю вздовж осі , то еліпсоїд Френеля вироджується в еліпсоїд обертання, що характеризує одновісний кристал з оптичною віссю вздовж осі  . .
Будь-яку площину, проведену через оптичну вісь, називають головним перетином кристала.
При поширенні світлових хвиль в анізотропному середовищі з напрямом коливань вздовж головних напрямів  , ,  , ,  фазові швидкості мають той же напрям, що і вектор фазові швидкості мають той же напрям, що і вектор  . У цьому випадку на основі (1) отримаємо . У цьому випадку на основі (1) отримаємо
 ; ;  ; ;  . .

Однак при довільному напрямі коливань вектор фазової швидкості хвилі неколінеарний вектору  , що характеризує також напрям світлового променя і групової швидкості хвилі. , що характеризує також напрям світлового променя і групової швидкості хвилі.
Нехай лінійно поляризована плоска світлова хвиля розповсюджується вздовж осі  , причому вектор , причому вектор  складає кут складає кут  з віссю з віссю  (рис. 2). (рис. 2).
Розкладемо початкове коливання  на дві що складають, одна з яких має напрям вздовж осі на дві що складають, одна з яких має напрям вздовж осі  , а інша – вздовж осі , а інша – вздовж осі  . Таким чином, в кристалі вздовж осі . Таким чином, в кристалі вздовж осі  розповсюджуються дві хвилі з різними фазовими швидкостями розповсюджуються дві хвилі з різними фазовими швидкостями  і і  . На виході кристала між цими хвилями виникає різниця фаз . На виході кристала між цими хвилями виникає різниця фаз
 , ,
де  – товщина кристала. – товщина кристала.
У залежності від значення  між двома хвилями виникає різниця фаз між двома хвилями виникає різниця фаз  , що в загальному випадку призводить до еліптичної поляризації. , що в загальному випадку призводить до еліптичної поляризації.
При 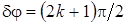 , де , де  , і , і  виконуються умови виникнення кругової поляризації, і лише при виконуються умови виникнення кругової поляризації, і лише при  зберігається лінійна поляризація світлової хвилі. зберігається лінійна поляризація світлової хвилі.
В анізотропних середовищах має місце подвійне променезаломлення. Пояснимо це явище на прикладі одноосного кристала. Нехай з повітря на кристал під кутом  падає пучок неполяризованого світла, причому для даного кристала падає пучок неполяризованого світла, причому для даного кристала  і оптична вісь направлена по осі і оптична вісь направлена по осі  . Визначимо . Визначимо  , а , а  . .
Розкладемо падаючу хвилю на дві, що складають, в одній з яких вектор  коливається вздовж осі коливається вздовж осі  , а в іншій – в площині
, а в іншій – в площині  . Для цих хвиль на основі закону заломлення можна написати такі співвідношення: . Для цих хвиль на основі закону заломлення можна написати такі співвідношення:
 ; ;
 . .
Рисунок 3 – Хвильова поверхня кристалів
Оскільки  , то , то  , і заломлені промені розповсюджуються в кристалі в двох різних напрямах. Отже, на межі ізотропного середовища з кристалом відбувається розкладання падаючих пучків світла на два непаралельних пучків, званих звичайним , і заломлені промені розповсюджуються в кристалі в двох різних напрямах. Отже, на межі ізотропного середовища з кристалом відбувається розкладання падаючих пучків світла на два непаралельних пучків, званих звичайним  і і  незвичайним, кожний з яких повністю лінійно поляризований. незвичайним, кожний з яких повністю лінійно поляризований.
Якщо  , кристали називають негативними, а при , кристали називають негативними, а при  – позитивними. У кристалах хвильова поверхня є подвійною, і у разі одноосных кристалів вона складається з сфери і еліпсоїда (рис. 4). – позитивними. У кристалах хвильова поверхня є подвійною, і у разі одноосных кристалів вона складається з сфери і еліпсоїда (рис. 4).
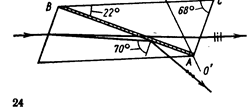
Рисунок 4 – Призма Ніколя
Для звичайної хвилі показник заломлення  не залежить від напряму поширення хвилі, а для незвичайної хвилі не залежить від напряму поширення хвилі, а для незвичайної хвилі  неоднаковий в різних напрямах. неоднаковий в різних напрямах.
Сфера і еліпсоїд торкаються один одного в двох точках  і і  , які визначають напрям оптичної осі , які визначають напрям оптичної осі  ,що співпадає з головною віссю симетрії кристала. Хвиля, що розповсюджується вздовж оптичної осі, не випробовує подвійного заломлення, а при поширенні хвилі перпендикулярно оптичної осі різниця ,що співпадає з головною віссю симетрії кристала. Хвиля, що розповсюджується вздовж оптичної осі, не випробовує подвійного заломлення, а при поширенні хвилі перпендикулярно оптичної осі різниця  і відповідна різниця фазовий швидкостей і відповідна різниця фазовий швидкостей  максимальні. максимальні.
Подвійне променезаломлення широко використовує для виготовлення поляризаторів. Розглянемо для прикладу призму Ніколя, що отримала широке практичне застосування (рис. 4).
Призму Ніколя звичайно виготовляють з прозорого кристала ісландського шпата (кальцита), що має сильне подвійне променезаломлення ( ; ; ). ).
Призму розпилюють, як показано на рис. 5, у напрямі  і склеюють ялицевим бальзамом з і склеюють ялицевим бальзамом з  . Таким чином, витримується співвідношення . Таким чином, витримується співвідношення  . .
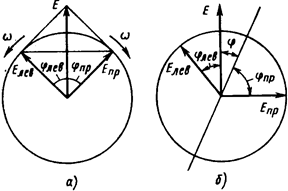
Рисунок 5- Лінійно поляризоване коливання
Пучок природного світла, входячи в призму Ніколя, випробовують подвійне променезаломлення і розділяються на два пучки: звичайний і незвичайний, які лінійно поляризовані у взаємно ортогональних напрямах.
На межі з ялицевим бальзамом виконується нерівність  , і звичайний промінь випробовує повне внутрішнє відображення, тобто повністю відхиляється в сторону. , і звичайний промінь випробовує повне внутрішнє відображення, тобто повністю відхиляється в сторону.
Незвичайний промінь, для якого  , проходить через шар ялицевого бальзаму і розповсюджується далі. Таким чином, призма Ніколя пропускає одні лінійно поляризовані пучки з інтенсивністю, приблизно рівній половині інтенсивності падаючих пучок. , проходить через шар ялицевого бальзаму і розповсюджується далі. Таким чином, призма Ніколя пропускає одні лінійно поляризовані пучки з інтенсивністю, приблизно рівній половині інтенсивності падаючих пучок.
Деякі середовища володіють здатністю обертати площину поляризації.
Ці середовища називають оптично активними. Прикладами таких середовищ є деякі одноосні кристали, наприклад кварц, а також аморфні речовини, наприклад, цукор, нікотин та ін. У одноосних оптично активних кристалах поворот площини поляризації відбувається при поширенні світла вздовж оптичної осі.
Обертання площини поляризації деякою мірою аналогічне подвійному променезаломленню. Для пояснення цього зазначимо спочатку, що будь-яке лінійно поляризоване коливання можна розкласти на два кругових коливання з правим і лівим обертанням (рис. 5, а). У оптично активній речовині швидкість поширення хвилі з лівим обертанням відмінна від швидкості поширення хвилі з правим обертанням.
Тому час, необхідний кожній хвилі для проходження одного і того ж відрізка в активному середовищі, що досліджується, виявиться різним. У результаті вектори  і і  повернуться на різні кути повернуться на різні кути  і і  , що еквівалентно повороту площини поляризації на кут , що еквівалентно повороту площини поляризації на кут  (рис. 5, б): (рис. 5, б):
 . .
Відмінність швидкостей хвилі в правообертаючому і лівообертаючому кристалічних речовинах пов'язано з асиметрією зовнішньої форми (відсутність центра симетрії), а у разі аморфних однорідних тіл з несиметричною будовою складних молекул активного середовища, що не мають ні центра, ні площини симетрії.
При високій щільності енергії оптичного випромінювання, яку можна забезпечити за допомогою сучасних лазерів, в ряді оптичних середовищ виникають нелінійні явища.
Спрощене якісне пояснення цих явищ полягає в наступному. Світлова хвиля, що розповсюджується в матеріальному середовищі розгойдує електрони середовища, відхилення яких від положення рівноваги у разі малої щільності енергії випромінювання пов'язане лінійною залежністю з напруженістю електричного поля хвилі. Коливальні електрони є джерелами повторних хвиль, які складаються між собою і з первинною хвилею, внаслідок чого формується сумарна світлова хвиля.
При збільшенні щільності енергії первинної хвилі лінійна залежність між відхиленням електронів і напруженістю електричного поля порушується, що призводить до того, що повторні хвилі, а отже, і сумарна хвиля містять різні кратні частоти первинної світлової хвилі. У процесі підсумовування (інтерференції) повторні хвилі можуть посилювати або послаблювати одна одну.
Умови, при яких відбувається утворення сумарної хвилі з частотами, відмінними від частоти первинної світлової хвилі, називають умовами просторового синхронізму.
Розглянемо одне з найпростіших нелінійних явищ - генерацію другої гармоніки. Нехай в нелінійному середовищі в напрямі  розповсюджується монохроматична світлова хвиля, яка відповідно до виразу (1.7) може бути записана у такому вигляді: розповсюджується монохроматична світлова хвиля, яка відповідно до виразу (1.7) може бути записана у такому вигляді:
 , ,
де  - показник заломлення середовища для світлової хвилі з частотою - показник заломлення середовища для світлової хвилі з частотою  ; ;  - швидкість світлової хвилі у вакуумі. - швидкість світлової хвилі у вакуумі.
У довільних точках  і і  виникають повторні хвилі на частоті виникають повторні хвилі на частоті  , яку можна описати такими виразами: , яку можна описати такими виразами:
 ; ;
де  - показник заломлення середовища для повторних хвиль з частотою - показник заломлення середовища для повторних хвиль з частотою  . .
З записаних виразів видно, що повторні хвилі після виникнення в точках  і і  розповсюджуються зі швидкістю розповсюджуються зі швидкістю  , яка відрізняється від швидкості первинної хвилі , яка відрізняється від швидкості первинної хвилі  . .
Повторні хвилі приходять в будь-яку точку  в однаковій фазі і посилюють одна одну тільки при виконанні рівності в однаковій фазі і посилюють одна одну тільки при виконанні рівності  , яка є умовою просторового синхронізму при подвоєнні частоти. , яка є умовою просторового синхронізму при подвоєнні частоти.
Генерацію другої гармоніки уперше спостерігали в 1961 р. при поширенні випромінювання рубінового лазера в одноосних кристалах. Для виконання умови просторового синхронізму був вибраний напрям, при якому  . .
Особливо ефективно явище спостерігається при використанні невидимого випромінювання з  , коли з нелінійного середовища вийде яскраво-зелене випромінювання з , коли з нелінійного середовища вийде яскраво-зелене випромінювання з  . .
Аналогічно можна пояснити генерацію сумарних і різнистних частот. Для спостереження цих явищ в нелінійне середовище необхідно ввести дві первинні хвилі з хвильовими векторами  і і  . У кожній точці нелінійного середовища виникають повторні хвилі з комбінаційними частотами . У кожній точці нелінійного середовища виникають повторні хвилі з комбінаційними частотами  і і  . .
Можна показати, що повторні хвилі з сумарною частотою  посилюють одна одну тільки при виконанні векторної умови просторового синхронізму, який має такий вигляд: посилюють одна одну тільки при виконанні векторної умови просторового синхронізму, який має такий вигляд:
 , ,
де  - хвильовий вектор світлової хвилі з сумарною частотою - хвильовий вектор світлової хвилі з сумарною частотою  . .
При наявності дисперсії ця умова не може бути виконана в изотропних середовищах.
Однак в кристалах при певних кутах між звичайними і незвичайними променями умова просторового синхронізму виконується. Можна вивести аналогічну умову просторового синхронізму для генерації різницевої частоти  і інших комбінаційних частот. і інших комбінаційних частот.
Якщо в середовищі розповсюджуються три хвилі, що задовольняють умові просторового синхронізму, між ними відбувається обмін енергією, і більш слабі хвилі посилюються (параметричне посилення). На цьому принципі працюють параметричні генератори світла, в яких можлива плавна перебудова частоти випромінювання.
Показник заломлення деяких ізотропних середовищ і кристалів, наприклад сірковуглеця, залежить від інтенсивності світлової хвилі. Якщо інтенсивність в поперечному перетині пучок нерівномірна, то показник заломлення середовища буде також нерівномірним, що еквівалентно неоднорідному середовищі.
При вісесиметричному розподілі інтенсивності світла в пучок і її плавній зміні від осі до периферії нелінійне середовище еквівалентне лінзі, і після такого середовища паралельні пучки стають такими, що сходяться або що розходяться.
Це явище називають самофокусовкою. Для спостереження самофокусовки потрібні порівняно високі потужності пучок. Енергетична освітленість, наприклад, у разі сірковуглеця складає приблизно  . .
Нелінійна оптика розвивається дуже швидко, і коло нелінійних оптичних явищ постійно розширяється. Росте також число практичних застосувань нелінійної оптики в різних оптико-електронних приладах.
|