Уравнения поверхности и линии в пространстве
Основные понятия
Поверхность и ее уравнение
Поверхность в пространстве, как правило, можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R
с центром в точке О
1
есть геометрическое место всех точек пространства, находящихся от точки О1на расстоянии R.
Прямоугольная система координат О
xyz
в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел x
, y
и z
– их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.
Уравнением данной поверхности в прямоугольной системе координат О
xyz
называется такое уравнение F
(
x
,
y
,
z
)=0
с тремя переменными x
, y
и z
, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности.
Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка М
1
(
x
1
;
y
1
;
z
1
)
на данной поверхности, достаточно подставить координаты точкиM1 в уравнение поверхности вместо переменных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют – не лежит.
Уравнение сферы
Найдем уравнение сферы радиуса R
c центром в точке О
1
(
x
0
;
y
0
;
z
0
)
. Согласно определению сферы расстояние любой ее точки М(
x
,
y
,
z
)
от центра О
1
(
x
0
;
y
0
;
z
0
)
равно радиусу R
, т.е. О
1
М =
R
. Но О
1
М=|
 |
, где |
, где  =(
x
-
x
0
;
y
-
y
0
;
z
-
z
0
).
Следовательно, =(
x
-
x
0
;
y
-
y
0
;
z
-
z
0
).
Следовательно,
 =R =R
или

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.
Если центр сферы О
1
совпадает с началом координат, то уравнение сферы принимает вид 
Если же дано уравнение вида F
(
x
;
y
;
z
) =0,
то оно, вообще говоря, определяет в пространстве некоторую поверхность.
Выражение «вообще говоря» означает, что в отдельных случаях уравнение F
(
x
;
y
;
z
) =0
может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».
Так, уравнению  не удовлетворяют никакие действительные значения x
,
y
,
z
.
Уравнению не удовлетворяют никакие действительные значения x
,
y
,
z
.
Уравнению 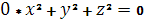 удовлетворяют лишь координаты точек, лежащих на оси О
x
(из уравнения следует: y
=0,
z
=0
, а x
- любое число). удовлетворяют лишь координаты точек, лежащих на оси О
x
(из уравнения следует: y
=0,
z
=0
, а x
- любое число).
Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:
1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.
2. Дано уравнение F
(
x
;
y
;
z
)=0.
Исследовать форму поверхности, определяемой этим уравнением.
Уравнение линии в пространстве
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 1) или как геометрическое место точек, общих двум поверхностям.
Если F
1
(
x
;
y
;
z
)=0
и F
2
(
x
;
y
;
z
)=0
– уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

Уравнения этой системы называются уравнениями линии в пространстве.
Например,  есть уравнения оси О
x
. есть уравнения оси О
x
.
 Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 2). В этом случае ее задают векторным уравнением Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 2). В этом случае ее задают векторным уравнением
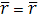 (t) (t)
Рис. 1 Рис. 2
или параметрическими уравнениями

Проекцией вектора на оси координат.
Например, параметрические уравнения винтовой линии
имеют вид
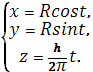
 Если точка М
равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка М
описывает винтовую линию (см. рис. 3). Если точка М
равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка М
описывает винтовую линию (см. рис. 3).
Рис. 3
|