Задача 1
Для стального трубчатого вала 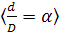 , который оборачивается с постоянной угловой скоростью, требуется: , который оборачивается с постоянной угловой скоростью, требуется:
1. Определить, пренебрегая трением в подшипниках, мощность на шкиве P0
.
2. Найти крутящиеся моменты, переданные каждым шкивом.
3. Построить эпюру моментов.
4. Из условия жесткости и крепости определить внутренний и внешний диаметры вала.
5. Построить эпюру углов закручивания по длине вала, приняв за недвижимый срез под первым левым шкивом.
Дано:
P1
= 24 кВт; a
= 1,2 м;α
= 0,8; G =
0,9·105
Мпа.
P
2
= 32 кВт; b
= 1,0 м; ω
= 130 рад/с;
P
3
= 27 кВт; c
= 0,4 м; [σ] = 180 МПа;
P
4
= 12 кВт; d
= 1,0 м; [θ] = 3,0º;
Решение:
Схема вала приведена на Рис. 1.
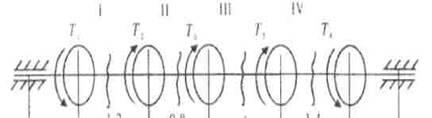
Рис. 1. Вал
Определяем мощность на шкиву P0
:
∑ Pi
= P
1
– P
2
- P
0
+ P
4
-
P
0
= 0;
P
0
= P
1
– P
2
– P
3
+ P
4
= 24 – 32 – 27 + 12 = - 23 кВт.
1. Определяем крутящиеся моменты на шкивах:
Т1
= 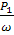 = = 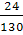 = 0,185 кНм; = 0,185 кНм;
Т2
= 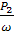 = = 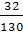 = 0,246 кНм; = 0,246 кНм;
Т3
= 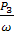 = = 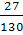 = 0,207 кНм; = 0,207 кНм;
Т4
= 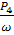 = = 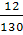 = 0,092 кНм; = 0,092 кНм;
Т0
= 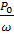 = = 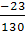 = - 0,177 кНм. = - 0,177 кНм.
2. Определяем крутящиеся моменты на участках вала:
Ткр1
= Т1
= 0,185 кНм;
Ткр2
= Т1
– Т2
= 0,185 – 0,246 = - 0,061 кНм;
Ткр3
= Т1
– Т2
– Т0
= - 0,061 + 0,177 = 0,116 кНм;
Ткр4
= Т1
– Т2
– Т0
– Т3
= 0,116 – 0,207 = - 0,091 кНм.
Строим епюру крутящих моментов. Максимальный крутящий момент на первом участке:
Ткр
max
= 0,185 кНм.
3. Определяем диаметр вала из условия прочности:
τ = 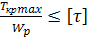
[τ]= 0,6·[σ] = 0,6·180 = 108 Мпа.
Для трубчатого вала
Wp
= 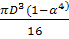
Тогда условие крепости будет
τ = 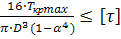
Из условия получаем
D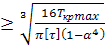 = = 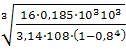 = = 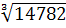 = 24,25 мм. = 24,25 мм.
Определяем диаметр вала из условия жесткости
Θ
=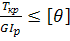 ; ;
Ip
= 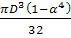 . .
Допустимый угол закручивания задан в градусах, а нужно в радианах, поэтому:
[θ]= 3,0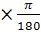 = 0,0523 рад/м. = 0,0523 рад/м.
Условие жесткости:
Θ
=
Из условия получаем:
D
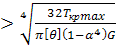 = = 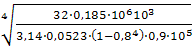 = 32,3 мм. = 32,3 мм.
Принимаем D
= 33 мм.
d
=
α·D
= 0,8·33 = 26,4 мм.
Тогда:
Ip
= 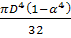 = = 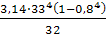 = 6,87·104
мм4 = 6,87·104
мм4
4. Найдем углы закручивания участков вала по формуле:
φi
= 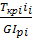 ; ;
φ1
= 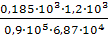 = 0,0359 рад = 2,06º; = 0,0359 рад = 2,06º;
φ2
= 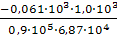 = - 0,00987 рад = - 0,565º; = - 0,00987 рад = - 0,565º;
φ3
= 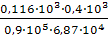 = 0,0075 рад = 0,43º; = 0,0075 рад = 0,43º;
φ4
= 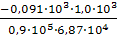 = - 0,0147 рад = - 0,84º. = - 0,0147 рад = - 0,84º.
Приняв за недвижимый срез под левым шкивом, строим эпюру угла закручивания:
α1
= 0;
α2
= φ1
= 2,06º;
α0
= φ1
+ φ2
= 2,06º + (-0,565º) = 1,495º;
α3
= φ1
+ φ2
+ φ3
= 1,925º;
α4
= φ1
+ φ2
+ φ3
+ φ4
= 1,085º.
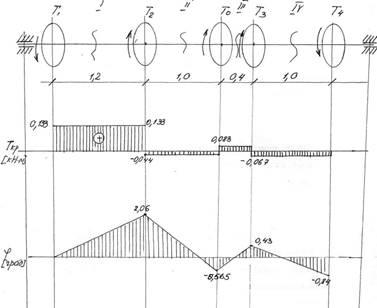
Рис. 2. Вал и его эпюры
Задача 2
Для статически определимого бруса квадратного ступенчато-переменного сечения, нагруженного показанными на рис.3 осевыми сосредоточенными нагрузками, требуется:
1. Построить эпюру продольных сил.
2. Из условия прочности определить площади и размеры сечений участков бруса.
3. Вычислить абсолютные продольные деформации участков бруса и построить эпюру его осевых перемещений.
4. Сделать эскиз ступенчатого бруса.
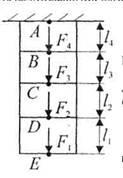
Рис.3. Ступенчатый брус
Дано:
F
1
= +94
kH
;
l
1
=2,6
м;
F
2
=-56
kH
; l
2
=2,0 м;
F
3
= +37 кН;
l
3
= 1,2 м;
F
4
= +84 кН;
l
4
=3,2 м;
[σ
]= 170 МПа;Е = 1,9·105
МПа.
Решение:
1. Изображаем в масштабе (по длине) брус и указываем нагрузку и размеры участков. На каждом участке проводим сечение и рассматриваем равновесие нижней отсеченной части, находим продольную силу в этих сечениях. Так как на исходном рисунке все силы направлены вниз, то продольная сила в любом сечении будет равна алгебраической сумме всех заданных сил, находящихся ниже данного сечения.
Сечение 1-1:
N
1
=
F
1
=94 кН;
Сечение 2-2:
N
2
=
F
1
+
F
2
=90+(-56)= 38 кН;
Сечение 3-3: N
3
=
F
1
+
F
2
+
F
3
=
90 + (-56) + 37 = 75 кН;
Сечение 4-4: N
4
=
F
1
+
F
2
+
F
3
+
F
4
= 90 + (-56) + 37 + 84 = 159 кН.
По этим данным строим эпюру N
,
учитывая, что на протяжении участка продольная сила постоянна.
2. Из условия прочности:
σ =
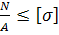
находим площади поперечных сечений участков бруса:
A
1
≥ 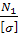 = = 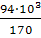 = 552,9 мм2
; = 552,9 мм2
;
а1
=
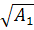 = =
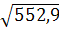 =
23,51 мм; =
23,51 мм;
A
2
≥ 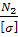 = = 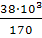 = 223,53 мм2
; = 223,53 мм2
;
а2
=
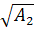 = =
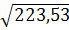 =
14,95 мм; =
14,95 мм;
A
3
≥ 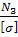 = = 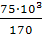 = 441,18 мм2
; = 441,18 мм2
;
а3
=
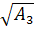 = =
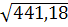 =
21 мм; =
21 мм;
А4
≥ 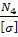 = = 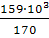 = 935,29 мм2
; = 935,29 мм2
;
а4
=
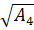 = =
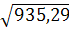 =
30,58 мм. =
30,58 мм.
Примечание: N
и [σ
] имеют одинаковый знак поэтому при вычислении площади поперечного сечения их значения берутся по модулю.
3.Определяем удлинения (укорочения) участка бруса:
Δ
l
1
=
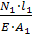 = =
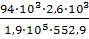 =
23,2 мм
; =
23,2 мм
;
Δ
l
2
=
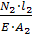 = =
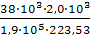 =
17,89 мм; =
17,89 мм;
Δ
l
3
=
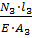 = =
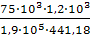 =
10,73 мм; =
10,73 мм;
Δ
l
4
=
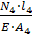 = =
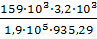 =
28,63 мм
. =
28,63 мм
.
Строим эпюру перемещений, для чего определяем перемещение точек А
,
В, С.
D
и Е.
σA
= 0;
σ
В
= σ
А
+ Δ
l
4
= 0 + 28,63 = 28,63 мм ;
σC
=
σ
В +
Δ
l
3
= 28,63 + 10,73 = 39,36 мм ;
σD
=
σC
+
Δ
l
2
= 39,36 + 17,89 = 57,25 мм
;
σE
= σD
+ Δ
l1
= 57,25 +23,2 =80,45мм
.
4.
Делаем эскиз ступенчатого бруса. Задача 3
Для заданной двухопорной балки, нагруженной двумя сосредоточенными силами F1
и F2
, равномерно распределенной нагрузкой q
и парой сил М,
требуется определить опорные реакции (Рис.5).
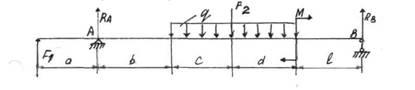
Рис.5. Схема нагрузки балки
Дано:
F1
= 32 кН; а = 1,0 м;
F2
= 12 кН; b
= 1,2 м;
q = 20 кН/м; с = 1,6 м;
М = 32 кН·м; d = 1,4 м;
l
= 1,2 м.
Решение:
1. Составляем уравнение равновесия балки:
∑МА
= 0;
- F1
·a – q
(c+d
) (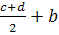 ) – F2
(b+c
) – M + RB
(b+c+d+l
) = 0; ) – F2
(b+c
) – M + RB
(b+c+d+l
) = 0;
∑МВ
= 0;
- F1
(a+b+c+d+l
) – RA
(b+c+d+l
) + F2
(d+l
) + q
(c+d
) (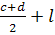 ) – M=
0; ) – M=
0;
2. Определяем реакции опор:
RB
=
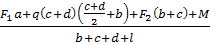 = =
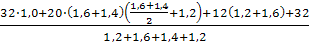 = =
= 48,07 кН
;
RA
=
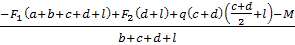 = =
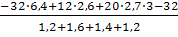 = =
= - 8,07 кН
;
Отрицательное значение RA
указывает, что направление силы RA
противоположно тому, которое изображено на рисунке, т.е. опорная реакция RA
направлена по вертиккали вниз.
Проверка:
∑ Fiy
= 0;
F
1
+
RA
-
F
2
–
q
(c
+
d
) +
RB
=
0;
32 – 8,07 – 12 - 20·3,0 + 48,07 = 0,
Потому
RA
=
- 8,07 кН
;
RB
=
48,07 кН.
Задача 4
Для заданной двухопорной балки, нагруженной двумя сосредоточенными силами, распределенной нагрузкой и парой сил, требуется:
1. Определить опорные реакции.
2.Построить эпюры поперечных сил и изгибающих моментов и определить сечение, в котором действует наибольший изгибающий момент.
3.Исходя из условия прочности по нормальным напряжениям, определить требуемый момент сопротивления и подобрать двутавровое, круглое и прямоугольное сечение (с заданным соотношением h
/
b
)
и сравнить их по экономичности, приняв для стали [σ]= 160 МПа.
Схема балки приведена на рис.6.
Дано:
а = 1,6 м;
b
= 1,2 м;
с = 1,0 м;
d
= 1,6 м;
l
= 1,4 м.
F
1
= 26 кН;
F
2
= 12 кН;
q
=
16 кН /м;
М = 32 кН·м;
h
/
b
=
2
.
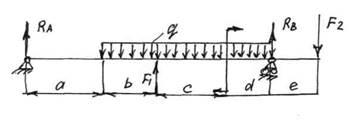
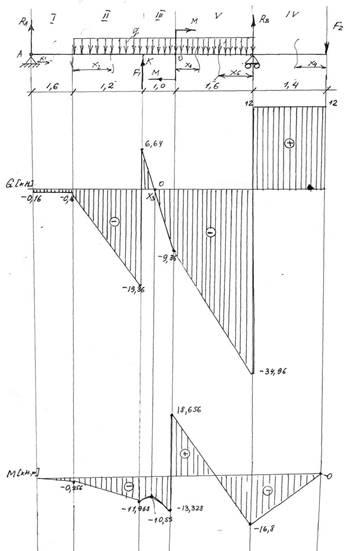
Рис. 6. Схема нагружения балки
Решение:
1.Определяем опорные реакции:
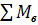 = 0; = 0;
-RA
·
5,4-
F
1
·
2,6 –
M
+
q·
3,8
·
1,9 -
F
2
·
1,4 = 0
RA
=
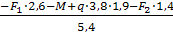 = - 0,16 кН; = - 0,16 кН;
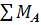 = 0; = 0;
R
В
·5,4 +
F
1
·
2,8-
q·
3,8
·
3,5 –М -
F
2
·
6,8 = 0
R
В
=
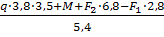 = 46,96 кН. = 46,96 кН.
Проверка:
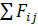 = 0. = 0.
RA
-
q·
3,8 +
F
1
+
R
В
-
F
2
= -0,16 – 60,8 + 26 + 46,96 – 12 = 0.
Значит, RA
= - 0,16 кН;
R
В
= 46,96 кН.
2. Разбиваем балку на 5 участков и, проведя на каждом участке произвольное сечение, определяем поперечную силу и изгибающий момент:
Участок I: 0≤ х1
≤ 1,6 м
Qx
1
= RA
= - 0,16 кН
Мx
1
= RA
·х1
= - 0,16
· х1
х1
= 0 МА
= 0
х1
= 1,6 м
МА
= -0,256 кН·м
Участок II: 0≤ х2
≤ 1,2 м
Qx
2
= RA
- q х2
Мx
2
= RA
(1,6 + х2
) - q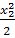 = -0,16(1,6 + х2
) - 16· = -0,16(1,6 + х2
) - 16·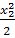
x2
= 0 Qx
2
= - 0,16 кН
Мx
2
= -0,256 кН·м
x2
= 1,2 м
Qк
= -19,36 кН
Мк
= -11,968 кН·м
Участок III: 0≤ х3
≤ 1,0 м
Q = RA
– q (1,2 + х3
) +F
1
= -0,16 – 16(1,2 +
х3
) + 26 = 25,84 – 16(1,2 + х3
)
М = RA
(2,8 + х3
) +F
1
·
х3
- 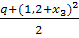 = -0,16(2,8+x3
) + 26 x3
- = -0,16(2,8+x3
) + 26 x3
- 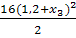
x3
= 0 Qk
= 6,64 кН
Мk
= -11,968 кН·м
x3
= 1,0м
Q = - 9,36 кН
М = -13,328 кН·м
Участок IV: 0≤ х4
≤ 1,4 м
Q = F
2
=12 кН
М = -F
2
х4
= -12 х4
х4
= 0 М = 0
х4
= 1,4 м
М = - 16,8 кН·м
Участок V: 0≤ х5
≤ 1,6 м
Q = F
2
–
RВ
+ q· х5
= 12 – 46,96 + 16 х5
= -34,96 + 16 х5
M
= -
F
2
(1,4 +
х5
) + RВ
х5
- q·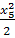 = -12(1,4 + х5
) +46,96 х5
- 16 = -12(1,4 + х5
) +46,96 х5
- 16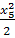
x5
= 0 Q = -34,96 кН
М = -16,8 кН·м
x5
= 1,6 м
Q = -9,36 кН
М = 18,656 кН·м
По полученным данным строим эпюры Q и М (рис.7).
На участке III поперечная сила Q принимает нулевое значение, поэтому в этом положении на эпюре «М» будет екстремум.
Qх
3
= 0;
25,84 – 16(1,2+х3
) = 0;
Х3
= 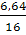 = 0,415 м = 0,415 м
М (0,415) = - 10,59 кНм;
Наибольшее значение изгибающего момента Мmax
=
18,856
кН·м
1. Из условия прочности по нормальным напряжениям:
σmax
= 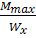 ≤[σ] ≤[σ]
находим требуемый момент сопротивления:
Wx
≥
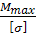 = =
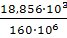 = 181 см3 = 181 см3
По таблицам сортамента выбираем двутавр № 20, у которого Wx
= 184 см3
а площадь поперечного сечения А = 26,8 см2.
Подбираем прямоугольное сечение:
Wx
=
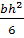
при h = 2·b
Wx
=
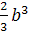
Откуда b = 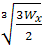 = = 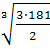 = 6,5 см = 6,5 см
h
= 2
b
= 13 см
А0
=
b·h
= 6,5
·
13= 84,5 см2
Подбираем круглое сечение
Wx
=
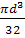
d
=
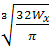 = 12,15 см = 12,15 см
А0
=
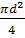 = =
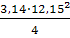 = 115,88 см2 = 115,88 см2
Находим отношение площадей, приняв площадь сечения двутавра за единицу:
А1
: Ао
: А0
= 1 : 3,15 : 4,32.
Список использованой литературы
1. Степин П.А. Сопротивление материалов: Учебник – М., Высшая школа , 1983 – 303 с.
2. Пособие к решению задач по сопротивлению материалов: Уч. пособие/ Миролюбов И.Н. и др. – М., Высшая школа, 1985 – 399с.
3. Тарг С.М. Краткий курс теоретической механики – М., Высшая школа, 1986 – 416 с.
4. Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике – М., Высшая школа, 1985 – 367 с.
5. Архипов О.Г., Кравцова Е.М., Галабурда Н.Ш. Механіка: Навч. посібник- Луганськ: Вид-во Східноукр. Нац. Ун-ту, 2005 – 256с.
|