Оптимальные линейные системы
Типичной прикладной задачей статистической радиотехники является оптимизация системы обработки сигнала  , присутствующего на входе совместно с шумом, описываемым случайным процессом  . В зависимости от цели обработки (обнаружение сигнала, различение двух или более сигналов, измерение параметров сигнала и т.п.) выбор оптимальной системы осуществляется на основе различных критериев оптимальности.
1. Параметрическая оптимизация
Простейшим методом оптимизации по заданному критерию является параметрическая оптимизация
, когда, в случае линейной системы, вид функциональной зависимости импульсного отклика системы от времени  или функции передачи системы в частотной области  считаются заданными с точностью до конечного числа неизвестных параметров этих зависимостей. Таким образом, структура линейной системы считается известной, необходимо определить лишь оптимальные значения тех или иных параметров этой структуры.
Другим методом оптимизации линейной системы является полная оптимизация
по заданному критерию, когда неизвестными являются функции , , или, иначе говоря, неизвестны не только параметры, но и сама структура системы. В этом случае целью оптимизации является нахождение оптимальных функций  или  .
Заметим, что вопрос оптимальности полученной системы в классе любых других возможных систем (не принадлежащих к классу линейных) при любом из таких методов оптимизации остается открытым.
Рассмотрим эти методы оптимизации на конкретных примерах.
2. Параметрическая оптимизация по критерию максимума отношения сигнал/шум
Рассмотрим обработку сигнала вида
на фоне «белого шума»  , имеющего энергетический спектр  вида
 .
В качестве критерия оптимальности выберем критерий максимума отношения  сигнала к шуму в некоторый момент времени  на выходе линейной системы. Подобная задача возникает в случае, когда, например, важным является обнаружение
полезного сигнала, причем восстановление его формы (воспроизведение
сигнала) не является необходимым.
Пусть  и  ‑ соответственно сигнал и шум на выходе рассматриваемой линейной системы. Тогда в момент :
 .
Выберем в качестве примера линейную систему, имеющую импульсный отклик
причем целью оптимизации является выбор значения  , обеспечивающего максимальное значение величины  .
Полезный сигнал на выходе системы определяется выражением:
Подставляя импульсный отклик рассматриваемой линейной системы, получаем:
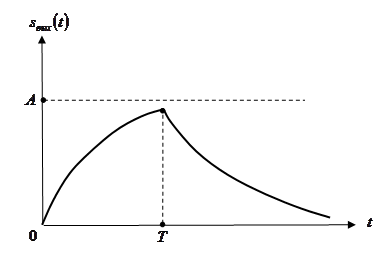
Итак,
 при 
С другой стороны, как было показано в 3,
Тогда в момент 
 .
После дифференцирования по  получаем уравнение для определения :
 ,
откуда
При этом
или
где
 и  ‑ энергия полезного сигнала.
3.
Параметрическая оптимизация по критерию минимума среднеквадратической ошибки воспроизведения полезного сигнала
Пусть теперь полезным сигналом является реализация некоторого случайного процесса  . Это может быть реализация сообщения при передаче речи или изображения, реализация сигнала в системе телеметрии и т.п. В таких условиях важным является не факт обнаружения полезного сигнала, а его воспроизведение на выходе линейной системы с возможно более высокой точностью. Поэтому в качестве критерия оптимальности целесообразно выбрать критерий минимума среднеквадратической ошибки (СКО) воспроизведения полезного сигнала на выходе линейной системы.
Пусть энергетические спектры процессов и равны соответственно
Полная ошибка  воспроизведения сигнала на выходе линейной системы описывается случайным процессом вида:
  ,
где  ‑ искажение сигнала в результате прохождения процесса  через рассматриваемую линейную систему.
Среднеквадратическая ошибка  , очевидно, равна:
где   ‑ энергетический спектр процесса  . В свою очередь по определению (см. 3.4):
где  ‑ спектр отрезка (длительностью  ) произвольной  -ой реализации процесса . Очевидно,
где  и  ‑ спектры отрезков (длительностью ) -ой реализации процессов и , а ‑ функция передачи рассматриваемой линейной системы в частотной области. Тогда
Выберем в качестве оптимизируемой линейной системы фильтр с характеристикой вида:
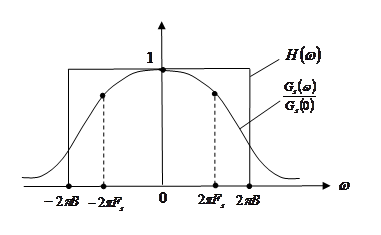
Тогда, очевидно,
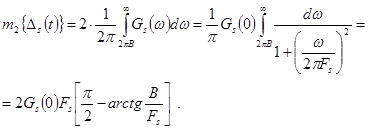
Кроме того, с учетом 3.12.2 имеем:
 .
Тогда полная СКО воспроизведения полезного сигнала:
Оптимальное значение  параметра  находим в результате решения уравнения:
откуда
С целью выявления физического смысла полученной зависимости введем в рассмотрение отношение сигнал/шум  на входе линейной системы. При этом средняя мощность  полезного сигнала с учетом результатов 3.12.2 равна:
Среднюю мощность шума  на входе линейной системы определим как среднюю мощность «белого шума» в некоторой полосе частот  , занимаемой полезным сигналом:
где определяется как половина ширины эквивалентного прямоугольника по формуле (см.3.6):
Подставляя рассматриваемую функцию  , получаем
Таким образом,
так что
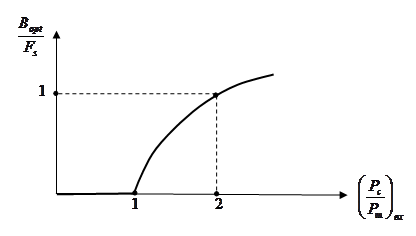
Вычислим теперь величину минимальной СКО воспроизведения полезного сигнала, соответствующую оптимальному выбору полосы  рассматриваемой линейной системы. В области  имеем:
Тогда минимальная относительная СКО
воспроизведения полезного сигнала равна 
Соответственно в области  когда  имеем:
 
4.
Оптимизация по критерию максимума отношения сигнал/шум
Рассмотрим, аналогично 1, обработку сигнала на фоне «белого шума» , по-прежнему используя в качестве критерия оптимальности критерий максимума отношения квадрата мгновенного значения сигнала  к средней мощности  шума на выходе системы. В отличие от 1, будем полагать форму сигнала  произвольной, а характеристику соответствующей линейной системы неизвестной. С учетом результатов 1 и 3 имеем:
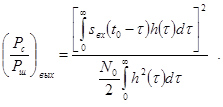
В силу неравенства Коши получаем:
так что
Легко видеть, что отношение достигает своего предельного значения, если
Линейная система с таким импульсным откликом называется фильтром
, согласованным с сигналом
. При этом действительно
Выбирая  , где ‑ момент окончания сигнала , имеем
так что
где  ‑ энергия сигнала .
Сравнивая полученный результат с отношением сигнал/шум на выходе линейной системы, рассмотренной в 4.1.1, легко видеть, что полная оптимизация в данном случае обеспечивает выигрыш в достигаемом значении отношения сигнал/шум, равный  дБ.
Функция передачи  согласованного фильтра в частотной области имеет вид:
где, при ,  ‑ функция, комплексно сопряженная со спектром  сигнала . В частности,  , откуда становится ясным физический смысл полученного результата: при мешающем воздействии в виде «белого шума» согласованный фильтр подавляет в большей степени относительно малые по амплитуде частотные составляющие сигнала , в определенном смысле «жертвуя» ими в целях более эффективного подавления «белого шума».
Рассмотрим теперь ситуацию, когда шум на входе оптимизируемой системы не является «белым», т.е. является «окрашенным», или коррелированным
, когда функция имеет произвольный вид, отличный от  -функции.
Представим характеристику рассматриваемой линейной системы в виде произведения
что соответствует каскадному соединению двух соответствующих линейных систем.
Выберем характеристику  так, чтобы она удовлетворяла соотношению:
Тогда на выходе первого каскада имеется сигнал  со спектром  и шум с энергетическим спектром  . Итак, рассматриваемая задача сводится к задаче оптимального приема сигнала на фоне «белого шума» с энергетическим спектром  . Следовательно, оптимальная характеристика  должна соответствовать характеристике фильтра, согласованного с сигналом :
где величина  определяется длительностью сигнала . Таким образом, характеристика искомой оптимальной системы имеет вид:
 .
В частности,
 .
Как видно из полученного соотношения, механизм оптимальной обработки сигнала в данном случае подобен механизму работы согласованного фильтра, однако, в дополнение к этому, оптимальная система подавляет в большей степени те частотные составляющие входного воздействия, которые соответствуют относительно большим составляющим энергетического спектра помехи .
5.Оптимизация по критерию минимума среднеквадратической ошибки воспроизведения полезного сигнала
Рассмотрим задачу воспроизведения полезного сигнала, представленного реализацией случайного процесса  , на фоне шума . По-прежнему энергетические спектры этих процессов обозначим соответственно и , однако, в отличие от 2, эти функции могут иметь произвольный вид, причем вид характеристики анализируемой линейной системы также заранее не известен.
С учетом результатов 2 в общем случае имеем:
 ,
так что суммарная СКО воспроизведения полезного сигнала:
 .
Представим полученное выражение в форме:
Представим сумму вещественных функций  как некоторую вспомогательную вещественную функцию  :
Тогда:
В полученном интеграле оба слагаемые подынтегрального выражения неотрицательны, причем лишь первое из них зависит от вида функции . Поэтому можно считать, что величина  достигает своего минимального значения, если выполняется соотношение:
 .
Следовательно, оптимальный вид функции определяется выражением:
 .
При этом величина СКО воспроизведения полезного сигнала, очевидно, вычисляется по формуле:
 .
Заметим, что в случае, когда энергетические спектры процессов и не перекрываются, величина  оказывается равной нулю, что и следовало ожидать. Далее, в условиях  , т.е. при отсутствии шума получаем  , что также имеет ясный физический смысл. В то же время в общем случае величина  принимает наименьшее значение на тех частотах, где величина максимальна. В этом смысле механизм оптимальной фильтрации по критерию минимума СКО воспроизведения полезного сигнала подобен механизму оптимальной фильтрации по критерию максимума отношения сигнал/шум на выходе системы.
Сравним теперь величину потенциально допустимой относительной СКО в рассмотренном случае с результатом параметрической оптимизации, полученным в 4.1.2. Итак, пусть
Тогда
Вычисляя интеграл и учитывая, что  и  , получаем:
 ,
откуда окончательно минимальная относительная СКО воспроизведения полезного сигнала равна:
 .
Полученный результат иллюстрируется на рисунке ниже. Здесь же пунктиром приведен соответствующий результат параметрической оптимизации в рассмотренном в частном случае использования фильтра с прямоугольной функцией передачи в частотной области.
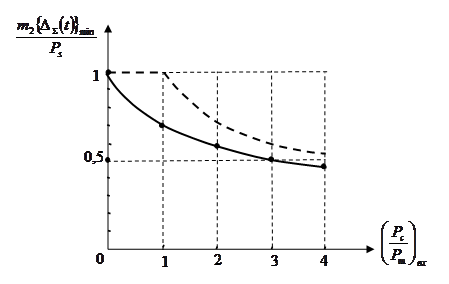
Как видно из приведенных выше зависимостей, полная оптимизация позволяет получить реальный выигрыш в величине СКО воспроизведения полезного сигнала в сравнении с параметрической оптимизацией.
|
