| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Филиал в г. Белебей республики Башкортостан
Кафедра ГиЕН
Курсовая работа
по высшей математике
Математические методы обработки результатов эксперимента
г. Белебей 2008 г.
Задача 1.
Провести анализ и обработку статистического материала выборок Х1, Х2, Х3.
Х1 – д. с. в. (n=100)
Применим метод разрядов.
xmax
= 1,68803
xmin
= 0,60271
Шаг разбиения:
h = 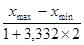
h = 0,14161
x0
= 0,53191
x1
= 0,81513
x2
= 0,95674
x3
= 1,09835
x4
= 1,23996
x5
= 1,38157
x6
= 1,52318
x7
= 1,80640
SR2
| xi-1
; xi
|
x0
; x1
|
x1
; x2
|
x2
; x3
|
x3
; x4
|
x4
; x5
|
x5
; x6
|
x6
; x7
|
| ni
|
13
|
11
|
15
|
13
|
16
|
12
|
20
|
| 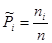
|
0,13
|
0,11
|
0,15
|
0,13
|
0,16
|
0,12
|
0,20
|
| 
|
0,91801
|
0,77678
|
1,05925
|
0,91801
|
1,12986
|
0,84740
|
1,41233
|
SR3
| 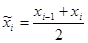
|
0,67352
|
0,88594
|
1,02755
|
1,16916
|
1,31077
|
1,45238
|
1,66479
|
| 
|
0,13
|
0,11
|
0,15
|
0,13
|
0,16
|
0,12
|
0,20
|
Статистическая средняя величина:


Вычисление статистической дисперсии и стандарта случайной величины
| 
|
-0,53458
|
-0,32216
|
-0,18055
|
-0,03894
|
0,10267
|
0,24428
|
0,45669
|
| 
|
0,28578
|
0,10379
|
0,03260
|
0,00152
|
0,01054
|
0,05967
|
0,20857
|
| Pi
|
0,13
|
0,11
|
0,15
|
0,13
|
0,16
|
0,12
|
0,20
|
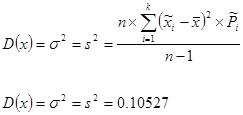

h1
= 0,91801
h2
= 0,77678
h3
= 1,05925
h4
= 0,91801
h5
= 1,12986
h6
= 0,84740
h7
= 1,41233
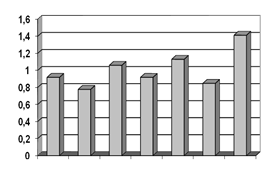
Можем выдвинуть гипотезу о равномерном распределении Х1. Числовые характеристики распределения найдем по формулам:
 и и 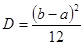 . .
M = 1,20810, D = 0,10527, откуда следует, что a= 0,64613 и b= 1,77007.
Функция плотности вероятности:
f(x) =
f(x) =
Теоретические вероятности:
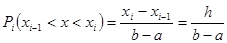
Р = 0,12599
Р>0,1, значит гипотеза не противоречит опытным данным.
Х2 – д. с. в. (n=100)
xmax
= -10,63734
xmin
= 27,11468
Шаг разбиения:
h = 4,92589
x0
= -13,10029
x1
= -3,24851
x2
= 1,67738
x3
= 6,60327
x4
= 11,52916
x5
= 16,45505
x6
= 31,23272
 SR2 SR2
| xi-1
; xi
|
x0
; x1
|
x1
; x2
|
x2
; x3
|
x3
; x4
|
x4
; x5
|
x5
; x6
|
| ni
|
8
|
15
|
26
|
22
|
18
|
11
|
| 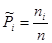
|
0,08
|
0,15
|
0,26
|
0,22
|
0,18
|
0,11
|
| 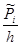
|
0,01624
|
0,03045
|
0,05278
|
0,04466
|
0,03654
|
0,02233
|
SR3
| 
|
-8,17440
|
-0,78557
|
4,14033
|
9,06622
|
13,99211
|
23,84389
|
| 
|
0,08
|
0,15
|
0,25
|
0,22
|
0,18
|
0,11
|
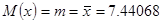
Вычисление статистической дисперсии и стандарта случайной величины
| 
|
-15,61508
|
-8,22625
|
-3,30035
|
1,62554
|
6,55143
|
16,40321
|
| 
|
243,83072
|
67,67119
|
10,89231
|
2,64238
|
42,92124
|
269,06530
|
| Pi
|
0,08
|
0,15
|
0,26
|
0,22
|
0,18
|
0,11
|
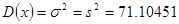
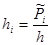
h1
= 0,01624
h2
= 0,03045
h3
= 0,05278
h4
= 0,04466
h5
= 0,03654
h6
= 0,02233
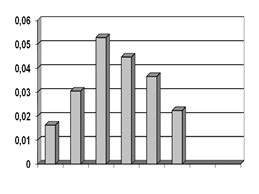
Можем выдвинуть гипотезу о нормальном распределении Х2.

| 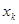
|
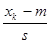
|
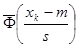
|
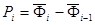
|
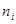
|

|
| -13,10029
|
-2,43597
|
-0,4918
|
0,0956
|
8
|
9,56
|
| -3,24851
|
-1,26764
|
-0,3962
|
| 0,1445
|
15
|
14,45
|
| 1,67738
|
-0,68347
|
-0,2517
|
| 0,2119
|
26
|
21,19
|
| 6,60327
|
-0,09931
|
-0,0398
|
| 0,2242
|
22
|
22,42
|
| 11,52916
|
0,48486
|
0,1844
|
| 0,1710
|
18
|
17,10
|
| 16,45505
|
1,06902
|
0,3554
|
| 0,1420
|
11
|
14,20
|
| 31,23272
|
2,82152
|
0,4974
|
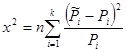
x2
=0.5724
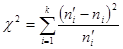

Следовательно, гипотеза не противоречит опытным данным.
Х3 – д. с. в. (n=100)
Применим метод разрядов.
xmax
= 1,45013
xmin
= 0,64637
Шаг разбиения:
h = 0,10487
x0
= 0,59394
x1
= 0,80368
x2
= 0,90855
x3
= 1,01342
x4
= 1,11829
x5
= 1,22316
x6
= 1,32803
x7
= 1,53777
SR2
| xi-1
; xi
|
x0
; x1
|
x1
; x2
|
x2
; x3
|
x3
; x4
|
x4
; x5
|
x5
; x6
|
x6
; x7
|
| ni
|
7
|
23
|
19
|
23
|
14
|
9
|
5
|
| 
|
0,07
|
0,23
|
0,19
|
0,23
|
0,14
|
0,09
|
0,05
|
| 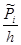
|
0,66749
|
2,19319
|
1,81178
|
2,19319
|
0,33499
|
0,85821
|
0,47678
|
SR3
| 
|
0,69881
|
0,85612
|
0,96099
|
1,06586
|
1,17073
|
1,27560
|
1,43290
|
| 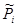
|
0,07
|
0,23
|
0,19
|
0,23
|
0,14
|
0,09
|
0,05
|
Статистическая средняя величина:

Вычисление статистической дисперсии и стандарта случайной величины
| 
|
-0,32511
|
0,16780
|
-0,06293
|
-0,68893
|
0,14681
|
0,25168
|
0,40896
|
| 
|
0,10570
|
0,02816
|
0,00396
|
0,47462
|
0,02155
|
0,06334
|
0,16726
|
| Pi
|
0,07
|
0,23
|
0,19
|
0,23
|
0,14
|
0,09
|
0,05
|

h1
= 0,66749
h2
= 2,19319
h3
= 1,81177
h4
= 2,19319
h5
= 1,33499
h6
= 0,85821
h7
= 0,47678
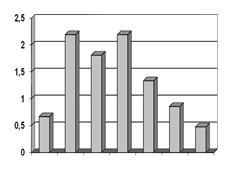
Можем выдвинуть гипотезу о экспоненциальном распределении Х3.

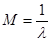 , , 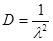
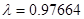 , , 

| x
|
f
|
| 0.2
|
0.80441
|
| 0.3
|
0.73004
|
| 0.4
|
0.66081
|
| 0.5
|
0.59932
|
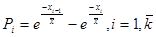
P1
= 0.10369
P2
= 0.04441
P3
= 0.04008
P4
= 0.03618
P5
= 0.03266
P6
= 0.02948
P7
= 0.05063

P = 0.33713
Значит, эксперимент не удался.
Задача 2
Пусть (x, z) – система двух случайных величин, где х – та случайная величина (Х1, Х2, Х3), которая распределена нормально. Определить, существует ли линейная корреляционная зависимость между этой случайной величиной и случайной величиной z.
Z – д. с. в. (n = 100)
Применим метод разрядов.
zmax
= -19.25521
zmin
= 56.81482
Шаг разбиения:
h = 9.925563
z0
= -24.21803
z1
= -4.36677
z2
= 5.55886
z3
= 15.48449
z4
= 25.41012
z5
= 35.33575
z6
= 65.11264
 SR2 SR2
| zi-1
; zi
|
z0
; z1
|
z1
; z2
|
z2
; z3
|
z3
; z4
|
z4
; z5
|
z5
; z6
|
| ni
|
10
|
19
|
25
|
22
|
16
|
8
|
| 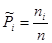
|
0,1
|
0,19
|
0,25
|
0,22
|
0,16
|
0,08
|
| 
|
0,01007
|
0,01914
|
0,02519
|
0,02216
|
0,01612
|
0,00806
|
SR3
| 
|
-14,2924
|
0,59605
|
10,52168
|
20,44731
|
30,37294
|
50,22420
|
| 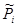
|
0,1
|
0,19
|
0,25
|
0,22
|
0,16
|
0,08
|
Статистическая средняя величина:
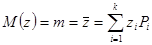

Вычисление статистической дисперсии и стандарта случайной величины
| 
|
-28,98285
|
-14,0944
|
-4,16877
|
5,75686
|
15,68249
|
35,53375
|
| 
|
840,00560
|
198,65211
|
17,37864
|
33,14144
|
245,94049
|
1262,64739
|
| Pi
|
0,1
|
0,19
|
0,25
|
0,22
|
0,16
|
0,08
|
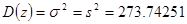

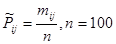
P11
= 0.06
P21
= 0.03
P22
= 0.15
P23
= 0.02
P32
= 0.05
P33
= 0.18
P43
= 0.05
P44
= 0.16
P45
= 0.01
P54
= 0.06
P55
= 0.12
P65
= 0.03
P66
= 0.08
Матрица вероятностей
| x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
| z1
|
0.06
|
0.03
|
0
|
0
|
0
|
0
|
| z2
|
0.03
|
0.15
|
0.05
|
0
|
0
|
0
|
| z3
|
0
|
0.02
|
0.18
|
0.05
|
0
|
0
|
| z4
|
0
|
0
|
0
|
0.16
|
0.06
|
0
|
| z5
|
0
|
0
|
0
|
0.01
|
0.12
|
0.03
|
| z6
|
0
|
0
|
0
|
0
|
0
|
0.08
|
Закон распределения системы 
| -8,17440
|
-0,78557
|
4,14033
|
9,06622
|
13,99211
|
23,84389
|
| -28,98285
|
0.06
|
0.03
|
0
|
0
|
0
|
0
|
| -14,0944
|
0.03
|
0.15
|
0.05
|
0
|
0
|
0
|
| -4,16877
|
0
|
0.02
|
0.18
|
0.05
|
0
|
0
|
| 5,75686
|
0
|
0
|
0
|
0.16
|
0.06
|
0
|
| 15,68249
|
0
|
0
|
0
|
0.01
|
0.12
|
0.03
|
| 35,53375
|
0
|
0
|
0
|
0
|
0
|
0.08
|
Закон распределения системы 
| -15,61508
|
-8,22625
|
-3,30035
|
1,62554
|
6,55143
|
16,40321
|
| -43,6733
|
0.06
|
0.03
|
0
|
0
|
0
|
0
|
| -28,78485
|
0.03
|
0.15
|
0.05
|
0
|
0
|
0
|
| -18,85922
|
0
|
0.02
|
0.18
|
0.05
|
0
|
0
|
| -8,93359
|
0
|
0
|
0
|
0.16
|
0.06
|
0
|
| 0,99204
|
0
|
0
|
0
|
0.01
|
0.12
|
0.03
|
| 20,8433
|
0
|
0
|
0
|
0
|
0
|
0.08
|
Корреляционный момент связи 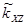
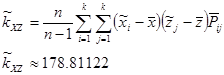
Следовательно, x и z – зависимы.
Коэффициент корреляции равен
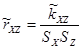
Sx
= 8.43235 Sz
= 16.54517
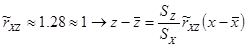
z = 2.5115x – 3.99682
|