задача № 1
Произведите группировку магазинов 1…22 по признаку численность продавцов, образовав при этом 5 групп с равными интервалами.
Сказуемое групповой таблицы должно содержать следующие показатели:
1. число магазинов
2. численность продавцов
3. размер товарооборота
4. размер торговой площади
5. размер торговой площади, приходящийся на одного продавца
6. уровень производительности труда (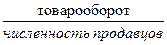 ) )
Примечание: в п.п. 2-4 показатели необходимо рассчитать в сумме и в среднем на один магазин
Решение:
Определяем длину интервала:
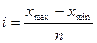
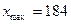
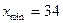

Строим групповую таблицу распределение магазинов по численности продавцов:
Таблица 1.1.
| № группы
|
Группировка магазинов по численности продавцов
|
Число магазинов
|
Чиленность продавцов, чел
|
товарооборота (млн.руб.)
|
Торговая площадь, кв.м
|
Размер торговой площади, приходяшийся на одного продавца
|
уровень производительности труда
|
| 34-64 |
10 |
41 |
80 |
946 |
23,073 |
1,951 |
| 40 |
113 |
1435 |
35,875 |
2,825 |
| 50 |
142 |
1256 |
25,120 |
2,840 |
| 57 |
156 |
1138 |
19,965 |
2,737 |
| 62 |
130 |
1246 |
20,097 |
2,097 |
| 60 |
184 |
1332 |
22,200 |
3,067 |
| 34 |
96 |
680 |
20,000 |
2,824 |
| 38 |
95 |
582 |
15,316 |
2,500 |
| 40 |
101 |
990 |
24,750 |
2,525 |
| 50 |
148 |
1354 |
27,080 |
2,960 |
| ИТОГО
|
10
|
472
|
1245
|
10959
|
| В среднем на один магазин
|
47,2
|
124,5
|
1095,9
|
| 64 - 94 |
3 |
64 |
148 |
1070 |
16,719 |
2,313 |
| 85 |
180 |
1360 |
16,000 |
2,118 |
| 92 |
132 |
1140 |
12,391 |
1,435 |
| ИТОГО
|
3
|
241
|
460
|
3570
|
| В среднем на один магазин
|
80,333
|
153,333
|
1190
|
| 94 - 124 |
6 |
105 |
280 |
1353 |
12,886 |
2,667 |
| 100 |
213 |
1216 |
12,160 |
2,130 |
| 112 |
298 |
1352 |
12,071 |
2,661 |
| 106 |
242 |
1445 |
13,632 |
2,283 |
| 109 |
304 |
1435 |
13,165 |
2,789 |
| 115 |
252 |
1677 |
14,583 |
2,191 |
| ИТОГО
|
6
|
647
|
1589
|
8478
|
| В среднем на один магазин
|
107,833
|
264,833
|
1413
|
| 124-154 |
2 |
130 |
314 |
1848 |
14,215 |
2,415 |
| 132 |
235 |
1335 |
10,114 |
1,780 |
| ИТОГО
|
2
|
262
|
549
|
3183
|
| В среднем на один магазин
|
131
|
274,5
|
1591,5
|
| 154 - 184 |
1 |
184 |
300 |
1820 |
9,891 |
1,630 |
| ИТОГО
|
1
|
184
|
300
|
1820
|
| В среднем на один магазин
|
184
|
300
|
1820
|
| ВСЕГО
|
22
|
1806
|
4143
|
28010
|
Задача №2
Используя построенный в задаче №1 интервальный ряд распределения магазинов по численности продавцов, определите:
1. среднее квадратическое отклонение
2. коэффициент вариации
3. модальную величину
Постройте гистограмму распределения и сделайте выводы.
Решение:
1. Среднеквадратическое отклонение представляет вычисляется по формуле:
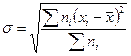
Для нахождения характеристики ряда распределения строим таблицу 2.1.
Таблица 2.1.
| Группировка магазинов по численности продавцов
|
Число магазинов, 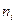
|
Середина интервала, 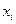
|
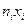
|
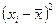
|
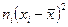
|
| 34-64 |
10 |
49 |
490 |
1162,19 |
11621,901 |
| 64-94 |
3 |
79 |
237 |
16,73554 |
50,207 |
| 94-124 |
6 |
109 |
654 |
671,281 |
4027,686 |
| 124-154 |
2 |
139 |
278 |
3125,826 |
6251,653 |
| 154-184 |
1 |
169 |
169 |
7380,372 |
7380,372 |
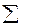
|
2
2
|
1828
|
29331,818
|
Вычисляем среднюю величину:
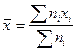

Среднеквадратическое отклонение:

2. Коэффициент вариации:

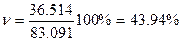
3. Модальная величина:
 мода – варианта с наибольшей частотой. мода – варианта с наибольшей частотой.
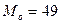

Рис.2.1. Гистограмма распределения.
Вывод:
Средняя величина количества продавцов составляет 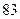 человек. Среднеквадратическое отклонение показывает, что значение признака в совокупности отклоняется от средней величины в ту или иную сторону в среднем человек. Среднеквадратическое отклонение показывает, что значение признака в совокупности отклоняется от средней величины в ту или иную сторону в среднем 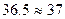 человек. человек.
По величине коэффициента вариации можно судить о степени вариации признака, а следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу. В нашем случае коэффициент вариации равен 44%, это говорит о том что разброс значений признака вокруг средней составляет 44%.
Задача №3
Проведено 6-процентное обследование качества поступившей партии товара. На основе механического способа отбора в выборочную совокупность взято 900 едениц, из которых 48 оказались бракованными. Средний вес одного изделия в выборке составил 10.8 кг, а среднее квадратическое отклонение – 0.35
Определите:
1. с вероятностью 0.954 пределы, в которых находится генеральная доля бракованной продукции
2. с вероятностью 0.997 пределы, в которых находится средний вес одного изделия во всей партии товара.
Решение:
1. Определим с вероятностью 95.4% возможные границы доли бракованной продукции.
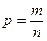
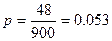
Доверительный интервал для доли бракованной продукции:
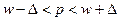 , где , где 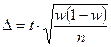
значение 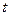 определяем по таблице распределения Лапласа: определяем по таблице распределения Лапласа:  ; ; 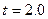
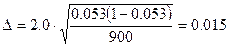
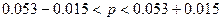
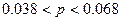
Таким образом, с вероятностью 95.4% мы можем утверждать, что доля бракованной продукции будет составлять от 3.8% до 6.8%
2. Определяем ошибку выборки:

где значение 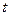 определяем по таблице распределения Лапласа: определяем по таблице распределения Лапласа:  ; ; 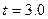
тогда:
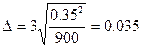
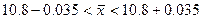
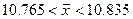
Таким образом, с вероятностью 99.7% мы можем утверждать, что средний вес одного изделия во всей партии товара будет, находится в пределах от 10.765 кг. до 10.835 кг.
Задача №4
Имеются следующие данные о продаже тканей торговой организацией ( в сопоставимых ценах) в 1994 – 1998 г.:
| Годы |
1994 |
1995 |
1996 |
1997 |
1998 |
| Продажа тканей , млн.руб. |
1.46 |
2.32 |
2.18 |
2.45 |
2.81 |
На основе приведенных данных:
1. Для анализа ряда динамики определите:
Для характеристики интенсивности динамики постройте соответствующий график.
2. Для анализа общей тенденции продажи тканей методом аналитического выравнивания:
Полученные результаты оформите в виде статистической таблицы. Сделайте выводы.
Решение:
1.1. Анализ ряда динамики
1. Абсолютный прирост  : :
· цепные:

· базисные:
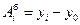
где 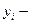 поточный (отчетный) уровень; поточный (отчетный) уровень; 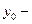 базисный уровень; базисный уровень;  предыдущий уровень предыдущий уровень
2. Темпы (коэффициент) роста 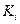 : :
· цепные:
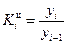
· базисные:

3. Темпы прироста 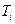 : :
· цепные:
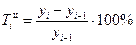
· базисные:
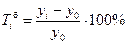
4. Абсолютное значение одного процента прироста 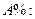
· цепные:
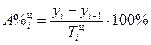
· базисные:

Все результаты расчетов по данным формулам представлены в таблице 3.1.
Таблица 3.1.
| годы
|
Продажа тканей, млн.руб
|
Показатели динамики
|
Абсолютный прирост 
|
Темпы (коэффициент) роста 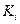
|
Темпы прироста 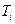
|
Абсолютное значение одного процента прироста 
|
| Базисные
|
Цепные
|
Базисные
|
Цепные
|
Базисные
|
Цепные
|
Базисные
|
Цепные
|
| 1994 |
1,46 |
- |
- |
- |
- |
- |
- |
- |
- |
| 1995 |
2,32 |
0,86 |
0,86 |
1,589 |
1,589 |
58,904 |
58,904 |
0,0146 |
0,0146 |
| 1996 |
2,18 |
0,72 |
-0,14 |
1,4932 |
0,9397 |
49,315 |
-6,034 |
0,0146 |
0,0232 |
| 1997 |
2,45 |
0,99 |
0,27 |
1,6781 |
1,1239 |
67,808 |
12,385 |
0,0146 |
0,0218 |
| 1998 |
2,81 |
1,35 |
0,36 |
1,9247 |
1,1469 |
92,466 |
14,694 |
0,0146 |
0,0245 |
1.2. Средние показатели динамики:
1. Средний уровень ряда динамики 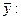
- интервального ряда:

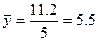
- моментного ряда:
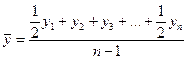
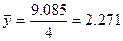
2. Средний абсолютный прирост 

или
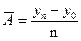
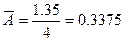
3. Средний коэффициент роста:
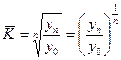
или


где, 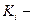 цепной коэффициент роста; цепной коэффициент роста; 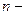 количество цепных коэффициентов количество цепных коэффициентов
4. Среднегодовой темп прироста (в процентах)
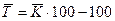
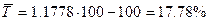
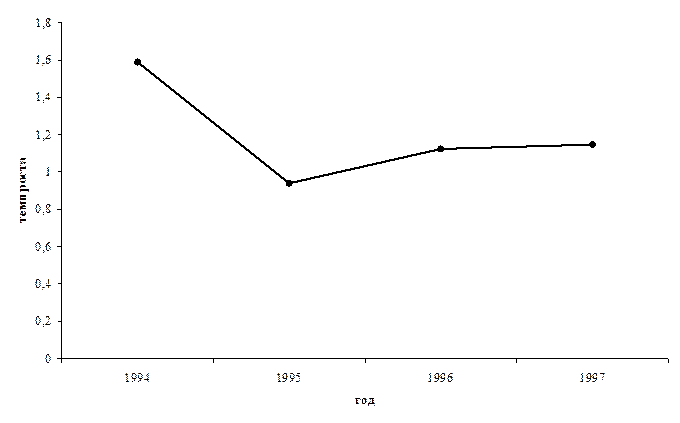
Рис.4.1. График интенсивности динамики.
Вывод:
Анализируя полученные показатели и график интенсивности мы можем сказать, что в 2003 году продажа тканей снизилась на 33% по сравнению с предыдущими годами, но начиная с 2004 года продажа тканей начала увеличиваться, т.е. в среднем ежегодно продажа тканей поднялась на 10.05%
2. Выявим основную тенденцию продажи тканей методом аналитического выравнивания по уравнению линейного тренда.
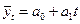
Нормальное уравнения служат для отыскания параметров при выравнивании по прямой. Для выравнивания по прямой 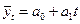 , система нормальных уравнений принимает вид: , система нормальных уравнений принимает вид:
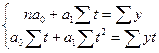
При 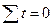 , ,
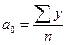 
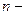 число членов ряда. число членов ряда.
Составим расчетную таблицу.
Таблица 3.2.
| годы
|
Продажа тканей,
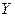 , млн.руб , млн.руб
|
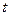 |
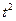 |
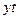 |
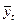 |
| 1994 |
1,46 |
-2 |
4 |
-2,92 |
1,674 |
| 1995 |
2,32 |
-1 |
1 |
-2,32 |
1,957 |
| 1996 |
2,18 |
0 |
0 |
0 |
2,24 |
| 1997 |
2,45 |
1 |
1 |
2,45 |
2,523 |
| 1998 |
2,81 |
2 |
4 |
5,62 |
2,806 |
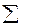
|
11,22
|
0
|
10 |
2,83 |
11,2 |
По приведенным выше формулам найдем:

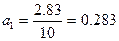
Уравнение прямой будет 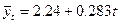 , расчетные значения , расчетные значения 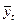 заносим в таблицу 3.2. заносим в таблицу 3.2.
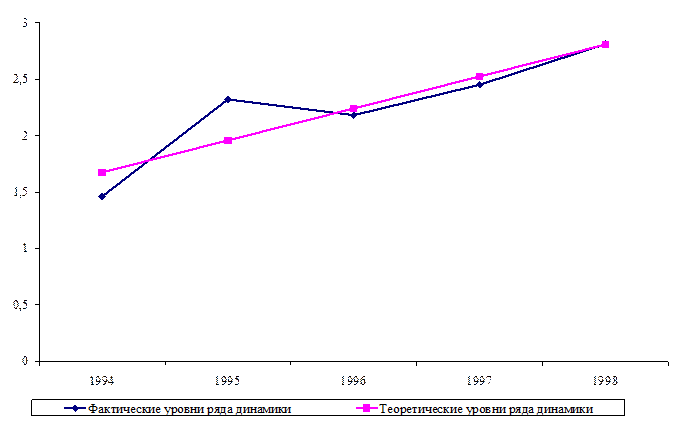
Рис.4.1. Фактические и теоретические значения продажи тканей
Продажу тканей в 1999 году 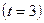 по формуле будет по формуле будет  млн.руб. млн.руб.
Вывод:
Естественно, эта величина условная, рассчитанная при предположении, что линейная закономерность продажи тканей , принятая для 1994-1998 гг., сохранится на последующий период до 1999 г.
Задача №
5
Имеются следующие данные о продаже товаров торговыми предприятием за три периода:
| Товары |
Количество, шт. |
Цена, руб.за 1 шт. |
| 1-й период |
2-й период |
3-й период |
1-й период |
2-й период |
3-й период |
| А |
115 |
102 |
120 |
75,2 |
78,4 |
82,2 |
| Б |
286 |
385 |
440 |
140,4 |
160,6 |
156,4 |
| В |
184 |
242 |
206 |
39,3 |
40,0 |
42,4 |
Определите индивидуальные и общие индексы: цен, физического объема товарооборота и товарооборота в фактических ценах на цепной и базисной основе. Покажите их взаимосвязь. Проведите сравнительный анализ.
Решение:
Для исчисления индивидуальных индексов применяются следующие формулы:
Индивидуальный индекс цен:
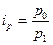
Где  цена за единицу количества продукта в текущем или отчетном периоде; цена за единицу количества продукта в текущем или отчетном периоде; 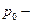 цена за единицу количества продукта в базисном периоде. цена за единицу количества продукта в базисном периоде.
Индивидуальный индекс физического объема:
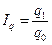
Где  количество реализованного товара в текущем периоде; количество реализованного товара в текущем периоде; 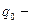 количество реализованного товара в базисном периоде. количество реализованного товара в базисном периоде.
Все расчеты занесем в таблицу
| Товар А
|
Индивидуальный индекс
|
pq
|
| Базисный
|
Цепной
|
| Количество, шт
|
1- й период
|
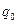 |
115 |
1 |
- |
8648 |
| 2-й период
|
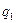 |
102 |
0,887 |
0,887 |
7996,8 |
| 3-й период
|
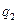 |
120 |
1,043 |
1,176 |
9864 |
| Цена
, руб.за 1 шт
|
1- й период
|
 |
75,2 |
1 |
- |
| 2-й период
|
 |
78,4 |
1,043 |
1,043 |
| 3-й период
|
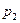 |
82,2 |
1,093 |
1,048 |
| Товар Б
|
Индивидуальный индекс
|
pq
|
| Базисный
|
Цепной
|
| Количество, шт
|
1- й период
|
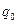 |
286 |
1 |
40154,4 |
| 2-й период
|
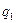 |
385 |
1,346 |
1,346 |
61831 |
| 3-й период
|
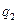 |
440 |
1,538 |
1,538 |
68816 |
| Цена
, руб.за 1 шт
|
1- й период
|
 |
140,4 |
1 |
| 2-й период
|
 |
160,6 |
1,144 |
1,144 |
| 3-й период
|
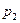 |
156,4 |
1,114 |
1,114 |
| Товар В
|
Индивидуальный индекс
|
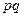
|
| Базисный
|
Цепной
|
| Количество, шт
|
1- й период
|
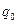 |
184 |
1 |
7231,2 |
| 2-й период
|
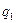 |
242 |
1,315 |
1,315 |
9680 |
| 3-й период
|
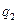 |
206 |
1,120 |
1,120 |
8734,4 |
| Цена
, руб.за 1 шт
|
1- й период
|
 |
39,3 |
1 |
| 2-й период
|
 |
40 |
1,018 |
1,018 |
| 3-й период
|
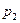 |
42,4 |
1,079 |
1,079 |
Формулы агрегатных цепных индексов стоимостного товарооборота, выражаются следующими отношениями:
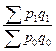 ; ; 
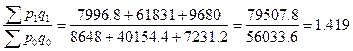

Формулы агрегатных базисных индексов стоимостного товарооборота за тот же период следующие:
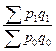 ; ; 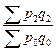
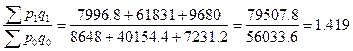
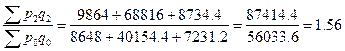
Пересчет цепных индексов стоимостного товарооборота в базисные, и наоборот, производится так же, как и индивидуальных индексов.
Произведение цепных агрегатных индексов стоимостного товарооборота образует базисный индекс стоимостного товарооборота.
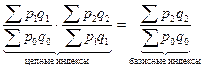

Вывод:
Базисные индексы показывают снижение продажи товаров торговым предприятием во 2-м периоде, а 3-м периоде повышение продажи товаров по сравнению с постоянной базой ( с уровнем 1-го периода).
Индексы с переменной базой (цепные) показывают, как увеличивалось продажа товаров торговыми предприятиями от одного периода к другому. При расчете базисных индексов принималась постоянная база сравнения (1-й период). При расчете цепных индексов принималась переменная база сравнения.
Задача №6
Деятельность торговой фирмы за два периода характеризуется следующими данными:
| Товары
|
Объем продажи товаров в фактических ценах, (тыс.руб.)
|
Среднее изменение цен, (%)
|
| 1-й период
|
2-й период
|
| А |
685 |
2540 |
+210 |
| Б |
434 |
735 |
+170 |
| В |
610 |
1816 |
+180 |
Определите:
1. Индивидуальные и общие индексы цен
2. Индивидуальные и общий индекс физического объема
3. Общий индекс товарооборота в фактических ценах
4. Прирост товарооборота во втором периоде по сравнению с первым периодом (общий и за счет действий отдельных факторов)
Решение:
1. Для исчисления индивидуального индекса цен применяются следующая формула:
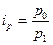
Где  цена за единицу количества продукта в текущем или отчетном периоде; цена за единицу количества продукта в текущем или отчетном периоде; 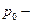 цена за единицу количества продукта в базисном периоде. цена за единицу количества продукта в базисном периоде.
Расчеты представлены в таблице 6.1:
Таблица 6.1.
| товары
|
Объем продажи товаров в фактических ценах, (тыс.руб.)
|
Среднее изменение цен, (%)
|
Индивидуальный индекс цен
|
Цена, тыс.руб.
|
Количество
|
| 1-й период
|
2-й период
|
1-й период
|
2-й период
|
1-й период
|
2-й период
|
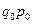
|
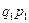
|
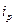
|

|

|
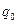
|
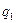
|
| А |
685 |
2540 |
+210 |
3.1 |
100 |
310 |
6.85 |
3.19 |
| Б |
434 |
735 |
+170 |
2.7 |
100 |
270 |
4.34 |
2.72 |
| В |
610 |
1816 |
+180 |
2.8 |
100 |
280 |
6.1 |
5.486 |
Общий индекс цен:
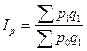
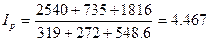 или 446.7% или 446.7%
Все расчеты представлены в таблице 6.1.
2. Индивидуальный индекс объема определяем по формуле:
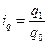
Продукт А:
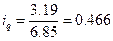
Продукт Б:

Продукт В:
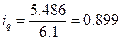
Общий индекс физического объема определяется по формуле:
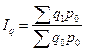
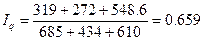 или 65.9% или 65.9%
3. Определяем общий индекс товарооборота:
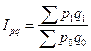
 или 294% или 294%
4.
1. Разница между числителем и знаменателем характеризует абсолютный прирост стоимости продукции за сентябрь и август.
 тыс.руб. тыс.руб.
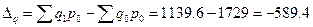 тыс.руб. тыс.руб.
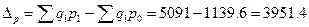 тыс.руб. тыс.руб.
Вывод:
По полученным результатам, мы можем сказать, что во 2-м периоде стоимостной объем продажи товаров по сравнению с 1-м периодом составил 294%, или увеличился на 194%.
Так же полученный индекс физического объема показывает, что физический объем товарооборота в отчетном периоде (2-й период) уменьшился по сравнению с базисным периодом (1-й период) на 34.1%.
Задача №7
Темпы роста товарооборота торгового предприятия в 1994 – 1998 г.г. составили (в % к предыдущему году)
| Годы |
1994 |
1995 |
1996 |
1997 |
1998 |
| Темп роста, (%) |
103.6 |
105.6 |
108.8 |
110.6 |
112.4 |
Известно, что в 1998 году товарооборот составил 26.6 млн.руб.
Определите:
1. Общий прирост товарооборота за 1994 – 1998 г.г. (в %).
2. Среднегодовой темп роста и прироста товарооборота.
3. Методом экстраполяции возможный размер товарооборота в 1999 г.
Решение:
1. Средний абсолютный прирост вычисляется по формуле:

Для определения товарооборота составляем таблицу:
Таблица 7.1.
| Год
|
Темп роста, %
|
Товарооборот, млн.руб
|

|
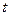
|
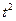
|
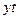
|
| 1994 |
103,6 |
18,63 |
- |
-2 |
4 |
-37,26 |
| 1995 |
105,6 |
19,67 |
1,04 |
-1 |
1 |
-19,67 |
| 1996 |
108,8 |
21,4 |
1,73 |
0 |
0 |
0 |
| 1997 |
110,6 |
23,67 |
2,27 |
1 |
1 |
23,67 |
| 1998 |
112,4 |
26,6 |
2,93 |
2 |
4 |
53,2 |
| Итого |
109,97 |
10 |
19,94 |
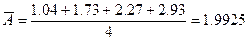
Общий прирост товарооборота составляет 7.97 млн.руб.
2. Среднегодовой темп роста можна рассчитать как среднюю геометрическую из годовых темпов роста:
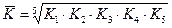
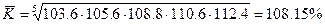
Среднегодовой прирост определяется по формуле:

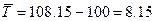
3. Выявим основную тенденцию продажи тканей методом аналитического выравнивания по уравнению линейного тренда.
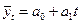
Нормальное уравнения служат для отыскания параметров при выравнивании по прямой. Для выравнивания по прямой 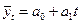 , система нормальных уравнений принимает вид: , система нормальных уравнений принимает вид:
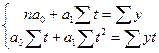
При  , ,
 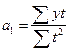
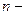 число членов ряда. число членов ряда.
Составим расчетную таблицу (таб.6.1)
По приведенным выше формулам найдем:
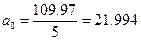
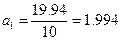
Товарооборот в 1999 году  по формуле будет по формуле будет 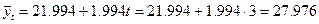 млн.руб. млн.руб.
Естественно, эта величина условная, рассчитанная при предположении, что линейная закономерность товарооборота , принятая для 1994-1998 гг., сохранится на последующий период до 1999 г.
3.
Задача №8
Используя исходные данные к задаче №1, рассчитайте парный коэффициент корреляции между объемом товарооборота и стоимостью основных фондов для магазинов №№1…22
Решение:
Для характеристики силы линейной корреляционной связи между величинами 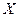 и и 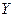 находим коэффициент корреляции: находим коэффициент корреляции:
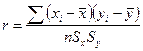
где 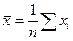 ; ; 
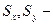 выборочные средние квадратического отклонения: выборочные средние квадратического отклонения:
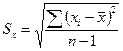 ; ; 
Для вычисления всех показателей составляем таблицу:
Таблица 8.1
| № п/п |
Товарооборот
,  , млн.руб. , млн.руб.
|
Стоимость основных фондов
,  , млн.руб , млн.руб
|
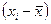 |
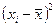 |
 |
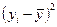 |
 |
| 1 |
148 |
5,3 |
-0,023 |
0,001 |
-44,864 |
2012,746 |
1,020 |
| 2 |
180 |
4,2 |
-1,123 |
1,261 |
-12,864 |
165,473 |
14,442 |
| 3 |
132 |
4,7 |
-0,623 |
0,388 |
-60,864 |
3704,382 |
37,901 |
| 4 |
314 |
7,3 |
1,977 |
3,910 |
121,136 |
14674,019 |
239,520 |
| 5 |
235 |
7,8 |
2,477 |
6,137 |
42,136 |
1775,473 |
104,383 |
| 6 |
80 |
2,2 |
-3,123 |
9,751 |
-112,864 |
12738,200 |
352,442 |
| 7 |
113 |
3,2 |
-2,123 |
4,506 |
-79,864 |
6378,200 |
169,529 |
| 8 |
300 |
6,8 |
1,477 |
2,182 |
107,136 |
11478,200 |
158,270 |
| 9 |
142 |
5,7 |
0,377 |
0,142 |
-50,864 |
2587,110 |
-19,189 |
| 10 |
280 |
6,3 |
0,977 |
0,955 |
87,136 |
7592,746 |
85,156 |
| 11 |
156 |
5,7 |
0,377 |
0,142 |
-36,864 |
1358,928 |
-13,908 |
| 12 |
213 |
5 |
-0,323 |
0,104 |
20,136 |
405,473 |
-6,499 |
| 13 |
298 |
6,7 |
1,377 |
1,897 |
105,136 |
11053,655 |
144,801 |
| 14 |
242 |
6,5 |
1,177 |
1,386 |
49,136 |
2414,382 |
57,847 |
| 15 |
130 |
4,8 |
-0,523 |
0,273 |
-62,864 |
3951,837 |
32,861 |
| 16 |
184 |
6,8 |
1,477 |
2,182 |
-8,864 |
78,564 |
-13,094 |
| 17 |
96 |
3 |
-2,323 |
5,395 |
-96,864 |
9382,564 |
224,988 |
| 18 |
304 |
6,9 |
1,577 |
2,488 |
111,136 |
12351,291 |
175,292 |
| 19 |
95 |
2,8 |
-2,523 |
6,364 |
-97,864 |
9577,291 |
246,883 |
| 20 |
352 |
8,3 |
2,977 |
8,864 |
159,136 |
25324,382 |
473,792 |
| 21 |
101 |
3 |
-2,323 |
5,395 |
-91,864 |
8438,928 |
213,374 |
| 22 |
148 |
4,1 |
-1,223 |
1,495 |
-44,864 |
2012,746 |
54,856 |
| cумма
|
4243
|
117,1
|
65,219
|
149456,591
|
2734,668
|
| среднее значение
|
192,864
|
5,323
|
Выборочное среднее квадратическое отклонение:
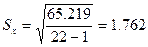 ; ;
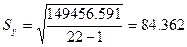
Тогда коэффициент корреляции будет равен:
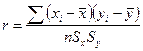

Таким образом, по значению 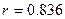 можно судить о том, что между объемом товарооборота и стоимостью основных фондов существует достаточно тесная корреляция. можно судить о том, что между объемом товарооборота и стоимостью основных фондов существует достаточно тесная корреляция.
|