ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА МАТЕМАТИКИ И ИНФОРМАТИКИ
ЛАБОРАТОРНАЯ РАБОТА
по эконометрике
Вариант № 1
Омск, 2010 г.
ПОСТАНОВКА ЗАДАЧИ
По данным, представленным в табл.1, изучается зависимость цены колготок от их плотности, состава и фирмы-производителя в торговых точках Москвы и Московской области весной 2006.
Таблица 1.
| № |
prise |
DEN |
polyamid |
lykra |
firm |
| Y
|
X1
|
X2
|
X3
|
X4
|
| 1 |
49,36 |
20 |
86 |
14 |
0 |
| 2 |
22,51 |
20 |
97 |
3 |
1 |
| 3 |
22,62 |
20 |
97 |
3 |
1 |
| 4 |
59,89 |
20 |
90 |
17 |
0 |
| 5 |
71,94 |
30 |
79 |
21 |
0 |
| 6 |
71,94 |
30 |
79 |
21 |
0 |
| 7 |
89,9 |
30 |
85 |
15 |
1 |
| 8 |
74,31 |
40 |
85 |
13 |
1 |
| 9 |
77,69 |
40 |
88 |
10 |
1 |
| 10 |
60,26 |
40 |
86 |
14 |
1 |
| 11 |
111,19 |
40 |
82 |
18 |
0 |
| 12 |
73,56 |
40 |
83 |
14 |
1 |
| 13 |
84,61 |
40 |
84 |
16 |
0 |
| 14 |
49,9 |
40 |
82 |
18 |
1 |
| 15 |
89,9 |
40 |
85 |
15 |
0 |
| 16 |
96,87 |
50 |
85 |
15 |
0 |
| 17 |
39,99 |
60 |
98 |
2 |
1 |
| 18 |
49,99 |
60 |
76 |
24 |
0 |
| 19 |
49,99 |
70 |
83 |
17 |
1 |
| 20 |
49,99 |
70 |
88 |
10 |
1 |
| 21 |
49,99 |
70 |
76 |
24 |
0 |
| 22 |
49,99 |
80 |
42 |
8 |
1 |
| 23 |
129,9 |
80 |
50 |
42 |
0 |
| 24 |
84 |
40 |
82 |
18 |
0 |
| 25 |
61 |
20 |
86 |
14 |
0 |
| 26 |
164,9 |
30 |
16 |
30 |
1 |
| 27 |
49,9 |
40 |
82 |
18 |
1 |
| 28 |
89,9 |
30 |
85 |
15 |
1 |
| 29 |
129,9 |
80 |
50 |
42 |
0 |
| 30 |
89,9 |
40 |
86 |
14 |
1 |
| 31 |
105,5 |
40 |
85 |
15 |
1 |
| 32 |
79,9 |
15 |
88 |
12 |
1 |
| 33 |
99,9 |
20 |
88 |
12 |
1 |
| 34 |
99,9 |
30 |
73 |
25 |
1 |
| 35 |
119,9 |
20 |
85 |
12 |
1 |
| 36 |
109,9 |
20 |
83 |
14 |
1 |
| 37 |
59,9 |
20 |
86 |
14 |
0 |
| 38 |
79,9 |
40 |
82 |
18 |
0 |
| 39 |
82,9 |
20 |
86 |
14 |
0 |
| 40 |
111,8 |
40 |
82 |
18 |
0 |
| 41 |
83,6 |
40 |
82 |
18 |
0 |
| 42 |
60 |
20 |
86 |
14 |
0 |
| 43 |
80 |
40 |
82 |
18 |
0 |
| 44 |
90 |
50 |
76 |
24 |
0 |
| 45 |
120 |
70 |
74 |
26 |
0 |
Цена колготок – это зависимая переменная Y. В качестве независимых, объясняющих переменных выбраны: плотность (DEN) Х1
, содержание полиамида Х2
и лайкры Х3
, фирма-производитель Х4
.
Описание переменных содержится в таблице 2.
Требуется:
1.
Рассчитать матрицу парных коэффициентов корреляции; оценить статистическую значимость коэффициентов регрессии.
2.
Оценить статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения проверить с помощью F-критерия; оценить качество уравнения регрессии с помощью коэффициента детерминации.
Таблица 2.
| Переменная |
Описание |
| № |
номер торговой точки |
| price |
цена колготок в рублях |
| DEN |
плотность в DEN |
| polyamid |
содержание полиамида в % |
| lykra |
содержание лайкры в % |
| firm |
фирма-производитель: 0 - Sanpellegrino, 1 - Грация |
3.
Построить уравнение множественной регрессии только со статистически значимыми факторами.
4.
Отобразить графически исходные данные и расчетные значения.
РЕШЕНИЕ ЗАДАЧИ
1. Рассчитать матрицу парных коэффициентов корреляции; оценить статистическую значимость коэффициентов регрессии.
Сначала нужно отобрать факторы, которые должны войти в модель. Для этого строится матрица коэффициентов парной корреляции (табл.3.)
Таблица 3.
| Y
|
X1
|
X2
|
X3
|
X4
|
| Y |
1 |
| X1 |
0,071711 |
1 |
| X2 |
-0,55678 |
-0,42189 |
1 |
| X3 |
0,607569 |
0,435579 |
-0,66726 |
1 |
| X4 |
-0,12119 |
-0,10354 |
0,060901 |
-0,43912 |
1 |
Анализ показал, что независимые переменные Х2
(полиамид) и Х3
(лайкра) имеют тесную линейную связь с результативным фактором Y. Проверяем наличие мультипликативности: │ 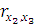 │= 0,66726. Считается, что две переменных явно коллинеарны, т.е. находятся между собой в линейной зависимости, если │= 0,66726. Считается, что две переменных явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 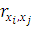 ≥ 0,7. Х2
и Х3
могут включаться в модель, т.к. мультипликативности нет. Х1
и Х4
в незначительной степени влияют на Y, их отбрасываем. ≥ 0,7. Х2
и Х3
могут включаться в модель, т.к. мультипликативности нет. Х1
и Х4
в незначительной степени влияют на Y, их отбрасываем.
Коэффициенты множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов. Для упрощения работы эти коэффициенты можно получить в Excel с помощью отчета по регрессии. Получаем уравнение линейной модели: у = -0,476х1
-0,588х2
+2,245х3
+7,554х4
+ 104,163.
Это означает, что с увеличением лайкры в составе колготок на 1%, их цена поднимется на 2,245 у.е. А при увеличении полиамида в составе колготок на 1%, их цена упадет на 0,588 у.е.
2. Оценить статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения проверить с помощью F-критерия; оценить качество уравнения регрессии с помощью коэффициента детерминации.
Подставляя значения факторов Х в уравнение регрессии, вычисляем урасч
,а записываем ряд остатков, составляем таблицу 4.
Таблица 4.
| № |
prise |
polyamid |
lykra |
у расч. |
остатки |
| Y
|
X2
|
X3
|
| 1 |
49,36 |
86 |
14 |
75,4920707 |
-26,1321 |
| 2 |
22,51 |
97 |
3 |
51,8771925 |
-29,3672 |
| 3 |
22,62 |
97 |
3 |
51,8771925 |
-29,2572 |
| 4 |
59,89 |
90 |
17 |
79,8758598 |
-19,9859 |
| 5 |
71,94 |
79 |
21 |
90,5623507 |
-18,6224 |
| 6 |
71,94 |
79 |
21 |
90,5623507 |
-18,6224 |
| 7 |
89,9 |
85 |
15 |
81,1152196 |
8,78478 |
| 8 |
74,31 |
85 |
13 |
71,8598003 |
2,4502 |
| 9 |
77,69 |
88 |
10 |
63,359152 |
14,33085 |
| 10 |
60,26 |
86 |
14 |
73,5171042 |
-13,2571 |
| 11 |
111,19 |
82 |
18 |
77,2971365 |
33,89286 |
| 12 |
73,56 |
83 |
14 |
75,2814724 |
-1,72147 |
| 13 |
84,61 |
84 |
16 |
71,6300376 |
12,97996 |
| 14 |
49,9 |
82 |
18 |
84,8513019 |
-34,9513 |
| 15 |
89,9 |
85 |
15 |
68,7964882 |
21,10351 |
| 16 |
96,87 |
85 |
15 |
64,0319222 |
32,83808 |
| 17 |
39,99 |
98 |
2 |
29,9853791 |
10,00462 |
| 18 |
49,99 |
76 |
24 |
84,769301 |
-34,7793 |
| 19 |
49,99 |
83 |
17 |
67,7240545 |
-17,7341 |
| 20 |
49,99 |
88 |
10 |
49,065454 |
0,924546 |
| 21 |
49,99 |
76 |
24 |
80,004735 |
-30,0147 |
| 22 |
49,99 |
42 |
8 |
66,8636812 |
-16,8737 |
| 23 |
129,9 |
50 |
42 |
130,949041 |
-1,04904 |
| 24 |
84 |
82 |
18 |
77,2971365 |
6,702864 |
| 25 |
61 |
86 |
14 |
75,4920707 |
-14,4921 |
| 26 |
164,9 |
16 |
30 |
155,377089 |
9,522911 |
| 27 |
49,9 |
82 |
18 |
84,8513019 |
-34,9513 |
| 28 |
89,9 |
85 |
15 |
81,1152196 |
8,78478 |
| 29 |
129,9 |
50 |
42 |
130,949041 |
-1,04904 |
| 30 |
89,9 |
86 |
14 |
73,5171042 |
16,3829 |
| 31 |
105,5 |
85 |
15 |
76,3506536 |
29,14935 |
| 32 |
79,9 |
88 |
12 |
79,7614203 |
0,13858 |
| 33 |
99,9 |
88 |
12 |
77,3791373 |
22,52086 |
| 34 |
99,9 |
73 |
25 |
110,626959 |
-10,727 |
| 35 |
119,9 |
85 |
12 |
79,1435056 |
40,75649 |
| 36 |
109,9 |
83 |
14 |
84,8106044 |
25,0894 |
| 37 |
59,9 |
86 |
14 |
75,4920707 |
-15,5921 |
| 38 |
79,9 |
82 |
18 |
77,2971365 |
2,602864 |
| 39 |
82,9 |
86 |
14 |
75,4920707 |
7,407929 |
| 40 |
111,8 |
82 |
18 |
77,2971365 |
34,50286 |
| 41 |
83,6 |
82 |
18 |
77,2971365 |
6,302864 |
| 42 |
60 |
86 |
14 |
75,4920707 |
-15,4921 |
| 43 |
80 |
82 |
18 |
77,2971365 |
2,702864 |
| 44 |
90 |
76 |
24 |
89,533867 |
0,466133 |
| 45 |
120 |
74 |
26 |
85,6718339 |
34,32817 |
Расчет остатков связан с тем, что изменение уi
будет неточно описываться изменением Х, поскольку присутствуют другие факторы, неучтенные в данной модели.
В Excel находим t-критерий для х2
и х3
. 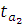 =-1,763; =-1,763;  =3,270. Сравним с табличным =3,270. Сравним с табличным 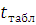 (0,05;42)=2,023. (0,05;42)=2,023.
При │tрасч
│>tα
связь существует и коэффициент корреляции является статистически значимым. В данном случае значимым является только а3
. На практике на а2
(коэффициент содержания полиамида в составе колготок при определении цены) опираться не стоит, т.к. этот коэффициент не является статистически значимым.
Приступая к оценке значимости уравнения множественной регрессии через критерий Фишера, найдем Fрасч
(есть в отчете по регрессии)=9,589 и Fтабл
(0,05;2;42)=3,220. Т.к. Fрасч
> Fтабл
, то модель является в целом надежной и по ней можно строить прогноз.
Оценить коэффициенты регрессии можно также с помощью коэффициента детерминации R2
. В данном случае он равен 0,4895 (из отчета по регрессии). Это говорит о том, что 48,95% всех случайных изменений у зависят от х и объясняются регрессионной моделью и учтены в ряде остатков. Для практического применения модели это очень маленький процент, и от нее следует отказаться. Для множественной регрессии применяют также скорректированный коэффициент детерминации 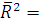 1-(1-R2
) 1-(1-R2
)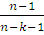 = 0,4385. Модель имеет низкую точность. = 0,4385. Модель имеет низкую точность.
3. Построить уравнение множественной регрессии только со статистически значимыми факторами.
Ранее был сделан вывод о том, что плотность колготок (х1
) и фирма-производитель (х2
) незначительно влияют на изменение цены (у) продукции. Таким образом, эти факторы можно отбросить.
В п.2. данной работы был проведен анализ коэффициентов корреляции, который показал, что а2
– коэффициент фактора содержания полиамида в составе колготок (х2
) – не является статистически значимым. Его также отбрасываем.
Уравнение принимает вид: у = 2,245х3
+ 104,163.
Таким образом, наиболее значимым фактором в изменениях цены (у) является содержание лайкры в составе колготок (х3
).
4. Отобразить графически исходные данные и расчетные значения.
Для отображения графически исходные значения цены и рассчитанные по модели цены лучше всего использовать Excel (диаграммы).
|