| Министерство образования Российской Федерации
Институт дистанционного образования
ГОУ ВПО «Тюменский государственный университет»
Контрольная работа
по дисциплине: «Теоретическая механика»
Выполнил студент Петренко Н.В.
Нижневартовск 2010
Вариант 5
Задача 5.1
К шарниру B прикреплён трос, перекинутый через блок и несущий груз силой тяжести G=60 кН. Углы на рис. 5.1 равны, соответственно: α=45º, β=90º, γ=50º. Рисунок не выдержан в масштабе. Определить силы реакции в стержнях АВ и АС. (стержень ВС).

Рис.5.1
Задача 5.2
По заданному графику проекции скорости точки (рис. 5.2), движущейся прямолинейно, построить графики ее перемещения и ускорения. Какой путь прошла точка? На каком максимальном расстоянии от исходного положения она находилась в процессе движения? На каком расстоянии от исходного положения она находится в конце движения?
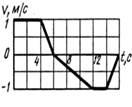
Рис. 5.2
Задача 5.3
В механизме качающегося грохота (рис.5.3) определить угловую скорость кривошипа О2
В=3r и скорость ползуна D при вертикальном положении кривошипа O1
A, если АВ=CD=2r. Отношение BC/CO2
=3/2, угловая скорость кривошипа О1
А равна ω=9 рад/с, углы α=45º, β=30º. Длина кривошипа O1
A равна r=0.1м.
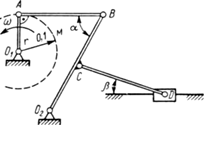
Рис.5.3
Задача 5.4
Доска длиной l=6м, свободно положенная на две разновысокие опоры А и В, получив начальную скорость v0
=0.2м/с, соскальзывает с опор вниз. Упадет ли доска с них, если коэффициент трения между доской и опорами f=0.3, а размеры на рис.0.4: a=0.4l, b=0.3l, h=0.15l.
Задача 5.5
На однородной балке массой m=3т (рис.5.5) установлена лебедка силой тяжести G=12кН, поднимающая на тросе, наматывающемся на барабан d=0.2l, груз силой тяжести Q=5кН с ускорением а=3м/с2
. Определить нагрузки на опоры А и В, если b=0.3l, c=0.1l. Массу троса не учитывать.
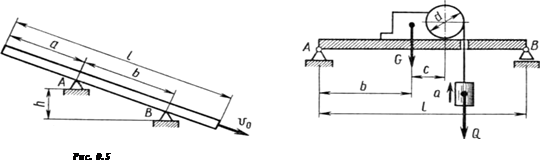
Рис.5.4 Рис.5.5
Решение
Задача 5.1
Все соединения считаем шарнирными, весом стержней пренебрегаем, трос считаем невесомым и нерастяжимым.
Решаем графоаналитическим методом с применением тригонометрических соотношений.
На шарнир В в направлении к блоку действует натяжение троса равное весу груза G
, вызывающее появление двух усилий направленных вдоль стержней АВ и ВС. При этом стержень АВ растягивается, а стержень ВС сжимается.
Так как рассматривается равновесие шарнира В, то отбросим стержни заменив их реакциями 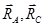 вместе с тремя силами вместе с тремя силами 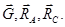
Силы 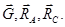 образуют уравновешенную систему, значит построенный из них треугольник является замкнутым. образуют уравновешенную систему, значит построенный из них треугольник является замкнутым.
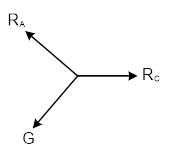 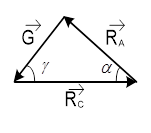
К полученному треугольнику применим теорему синусов:
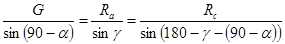 ; ;
Найдем модули сил:
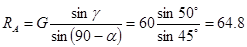 ; ;

Задача 5.2
График проекции скорости точки разобьем на пять отдельных участков (AB, BC, CD, DE и EF). Для каждого участка рассмотрим начальное (с индексом «н») и конечное (с индексом «к») значение какого либо параметра (время t, скорость v, перемещение S ).
Ускорение на любом из участков будем считать постоянным. Начальное значение параметра на последующем участке будем приравнивать к конечному значению параметра на предыдущем участке, например: значение 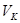 на участке АВ равно значению на участке АВ равно значению  на участке BC. на участке BC.
Для определения постоянного значения ускорения применим формулу
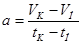
Для определения конечного значения перемещения на участке:
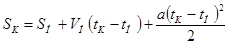
Значение параметров, определенные по заданному графику 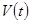 и по двум указанным формулам занесем в таблицу 5.2. и по двум указанным формулам занесем в таблицу 5.2.
Таблица 5.2
| участок
|
tн,c
|
tk,c
|
Vн, м/с
|
Vк , м/с
|
a , м/с2
|
Sн, м
|
Sк, м
|
/ Sк- Sн/
|
| A-B
|
0
|
4
|
1
|
1
|
0
|
0
|
4
|
4
|
| B-C
|
4
|
6
|
1
|
0
|
-1/2
|
4
|
5
|
1
|
| C-D
|
6
|
12
|
0
|
-1
|
-1/6
|
5
|
2
|
3
|
| D-E
|
12
|
14
|
-1
|
-1
|
0
|
2
|
0
|
2
|
| E-F
|
14
|
16
|
-1
|
0
|
1/2
|
0
|
-1
|
1
|
По значениям таблицы 5.2 построим графики 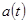 и и  . .
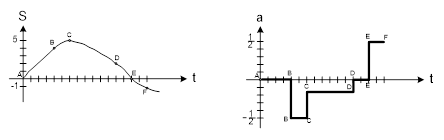
В последнем столбце приведено абсолютное значение пути пройденной точкой на данном участке. Очевидно, что путь, пройденный точкой, равен сумме абсолютных значений перемещения на всех участках т.е.
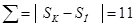 . .
Максимальное расстояние, на котором точка находилась от начального положения это Sк=5 на участке ВС - максимальное удаление. В конце движения точка Sк для участка E-F находится на расстоянии 1м. от исходного положения.
Задача 5.3
Механизм совершает плоскопараллельное движение. Ведущим звеном, движение которого задано, является кривошип ОА, совершающий вращение вокруг оси О. Определим модуль скорости конца кривошипа, т.е. точки А:
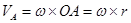
Вектор 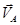 перпендикулярен ОА и направлен в сторону вращения кривошипа. Перейдем к звену АВ и найдем скорость точки В. Вектор перпендикулярен ОА и направлен в сторону вращения кривошипа. Перейдем к звену АВ и найдем скорость точки В. Вектор 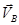 направлен перпендикулярно к звену ВО2
, т.к. точка В принадлежит одновременно и звену ВО2
, которое может вращаться вокруг точки О2.
Мгновенный центр скоростей звена АВ находится в точке Р – пересечения перпендикуляров к направлен перпендикулярно к звену ВО2
, т.к. точка В принадлежит одновременно и звену ВО2
, которое может вращаться вокруг точки О2.
Мгновенный центр скоростей звена АВ находится в точке Р – пересечения перпендикуляров к 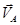 и и 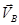 . .
Из ∆ АВР находим:
 ; ;
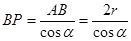
Так как вектор скорости любой точки Х звена АВ перпендикулярен отрезку ХР и направлен в строну вращения звена, то 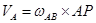 , отсюда: , отсюда:
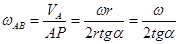 . .
Аналогично находим 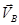 : :
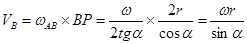
Перейдем к звену СО2
. Зная скорость точки В найдем 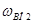 : :
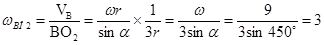
Точка С принадлежит звену ВО2
и вращается относительно О2
с угловой скоростью 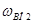 , следовательно: , следовательно:
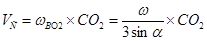
Далее рассмотрим движение звена СD. Спроецируем на ось Z, направленную вдоль движения ползуна D скорости точек  и и 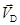 . По теореме о проекциях скоростей двух точек . По теореме о проекциях скоростей двух точек 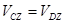 , т.к. , т.к. 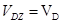 и и
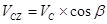 , то , то  . .
Т.к.
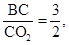
то
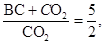
иначе

значит
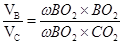 , ,
отсюда
 , ,
следовательно
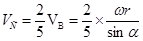 , ,
тогда
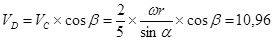
Задача 5.4
В центре доски приложена сила тяжести  , которую можно разложить на две составляющие: , которую можно разложить на две составляющие: 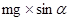 - направленную вдоль доски и - направленную вдоль доски и  - направленную перпендикулярно доске. В опорах А и В возникают реакции RА
и RB
соответственно, которые можно найти рассматривая равновесие доски относительно опор А и В. - направленную перпендикулярно доске. В опорах А и В возникают реакции RА
и RB
соответственно, которые можно найти рассматривая равновесие доски относительно опор А и В.
Сумма моментов сил относительно опоры А равна нулю:
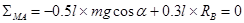 , ,
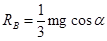 . .
Аналогично для узла В:
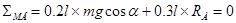 , ,
 . .
Силы трения в узлах равны:
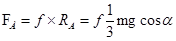 , ,
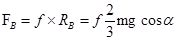 . .
Проекция сил, действующих на доску на ось Х , параллельную доске, движущейся с ускорением 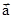 : :
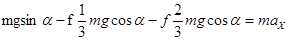 , ,
Отсюда найдем ускорение движения доски:

Из заданного рисунка видно, что
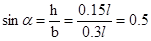
т.е. 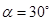 и тогда и тогда 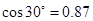 , далее получим: , далее получим:

Положительное значение ускорения в выбранном направлении оси х говорит о том, что происходит равноускоренное движение доски, которое при любом положительном значении начальной скорости 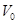 закончится падением доски. закончится падением доски.
Задача 5.5
На балку действует 4 силы: собственный вес 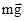 , приложенный на середине длины балки (0,5l от опоры А и опоры В), вес лебедки , приложенный на середине длины балки (0,5l от опоры А и опоры В), вес лебедки 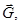 приложенный на расстояние b=0,3l от опоры А (и 0,7l от опоры В соответственно), вес поднимаемого груза Q, приложенный на расстоянии, равном приложенный на расстояние b=0,3l от опоры А (и 0,7l от опоры В соответственно), вес поднимаемого груза Q, приложенный на расстоянии, равном
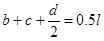
от опоры А ( и опоры В соответственно) и сила 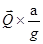 , заставляющая груз подниматься с ускорением ( здесь , заставляющая груз подниматься с ускорением ( здесь 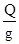 - масса груза). - масса груза).
Эти 4 воздействующие на балку силы вызывают реакции в опорах А и В, обозначим их 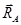 и и 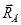 соответственно. соответственно.

Рассмотрим уравнение моментов сил относительно точки А. Моменты сил, стремящиеся вызвать поворот против часовой стрелки - примем положительными, а моменты сил направленные по часовой стрелке – отрицательными.
Для опоры А сумма моментов сил равна нулю, т.к. балка покоится:
 ; ;
Отсюда:

Если
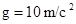 , ,
то

Аналогично для опоры В:
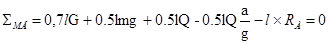
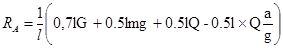
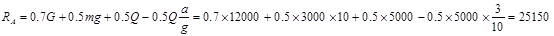
Литература
1. Тарг С.М. Краткий курс теоретической механики. М., 1963 и последующие издания.
2. Пилипенко В.А. Теоретическая механика, 2009 ТюмГУ
|