| Содержание
Введение
1. Основные понятия и определения
2. Топологическое представление радиоцепи
3. Расчет цепей на основе направленных графов
Список используемой литературы
Список обозначений
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ВЫСОКОЧАСТОНЫХ РАДИОЦЕПЕЙ
НА ОСНОВЕ НАПРАВЛЕННЫХ ГРАФОВ
Введение
В статье рассматриваются некоторые вопросы применения теории графов для расчета высокочастотных радиоцепей, описываемых матрицей рассеяния: составление графа цепи из нескольких 2 - полюсников, различные способы преобразования и примеры расчета.
1. Основные понятия и определения
Для расчетов радиоцепей большое распространение получили методы матричной алгебры. Однако эти методы применительно к анализу сложных цепей приводят к чрезвычайно трудоемким расчетам, затрудняют установление зависимостей между отдельными параметрами и представление исходной цепи в виде комплекса простых структур. Эти недостатки в значительной степени устраняются применением метода направленных графов [ 1, 2 ], сущность которого заключается в том, что матричные уравнения, описывающие систему, могут быть заменены соединениями элементарных графов, преобразования которых соответствуют матричным преобразованиям, но выполняются значительно проще. Преимущество этого метода также в том, что математическое описание задачи с помощью направленных графов естественным образом вытекает из физического строения системы и не требует записи исходных матричных уравнений. Направленный граф служит топологической формой представления уравнений системы относительно выбранных переменных, т.е. топологической моделью системы.
Рассмотрение топологических моделей высокочастотных цепей начнем с основных понятий теории графов. Необходимость этого вытекает из отсутствия единой терминологии и устранения возможности неправильного толкования отдельных терминов.
Графом
- называется система точек и связывающих их линий. Каждая точка - узел
графа; линия, связывающая две точки, - ветвь.
Направленный граф
- граф, в котором все ветви имеют направление, ненаправленный
- если ветви направления не имеют.
Направленному графу однозначно соответствует система линейных алгебраических уравнений, в которых узлы графа - переменные, а ветви - коэффициенты. Например системе уравнений
 (1) (1)
соответствует граф, приведенный на рис. 1.
Узлы, имеющие только выходящие ветви - источники; узлы, имеющие только входящие ветви - стоки. На рис.1. источники - и и  , сток - , сток -  . .
Путь
- непрерывная последовательность ветвей, вдоль которой каждый узел встречается не более одного раза. Если путь начинается и кончается в одной и той же точке, то он образует контур
. Если контур образован одной ветвью, то это - элементарный контур
. Дерево
- совокупность соединенных ветвей, касающихся всех узлов, но не образующих ни одного контура.
Каждая ветвь характеризуется величиной, называемой передачей ветви
. Например, ветвь, соединяющая  и и  , имеет передачу b. Величина пути , имеет передачу b. Величина пути
 - произведение передач ветвей пути k. Величина дерева
- произведение передач ветвей этого дерева. - произведение передач ветвей пути k. Величина дерева
- произведение передач ветвей этого дерева.
 
Рис. 1 Рис. 2
Определитель графа
 - сумма величин различных деревьев, содержащихся в данном графе. И, наконец, передача - сумма величин различных деревьев, содержащихся в данном графе. И, наконец, передача
 - сумма величин возможных путей между двумя узлами - сумма величин возможных путей между двумя узлами  и и  . .
в основе правил преобразования направленных графов потока сигналов лежит следующее утверждение - на величину сигнала в узде непосредственно влияют только входящие ветви; наличие выходных ветвей, если они не образуют элементарных контуров, на величину сигнала в узле не влияют. непосредственно влияют только входящие ветви; наличие выходных ветвей, если они не образуют элементарных контуров, на величину сигнала в узле не влияют.
Преобразования графов соответствуют преобразованиям, совершаемым с системой алгебраических уравнений, или, в более общем смысле, преобразованиям матрицы этой системы. Преобразования могут преследовать две цели - либо изменение структуры графа для более удобного (в каком-то смысле) установления зависимостей между величинами, либо для нахождения передачи между двумя узлами.
2.Топологическое представление радиоцепи
В теории электрорадио цепей существует несколько способов математического представления структуры цепи с помощью графов. Представления на основе токов и напряжений в качестве узловых переменных [ 1, 3 ] приводит к структурам графа, совпадающим с физической структурой электронной цепи. Радиотехнические цепи высоких и сверхвысоких частот также могут представлены [ 4 ] на основе полных токов и напряжений с использованием параметров матриц проводимостей и сопротивлений. Однако наибольший интерес для цепей с распределенными постоянными имеет представление на основе падающих и отраженных волн [ 5 ] , т.е. составляющих полных либо тока, либо, что чаще, напряжения. Если этот интерес определился ясным физическим смыслом и удобством параметров представления ( параметров матрицы рассеяния ), то с использованием графов сюда следует добавит другой важный фактор - совпадение физической структуры графа. Построение топологической модели сложной схемы начнем с простейшей - четырехполюсник, включенный между генератором и нагрузкой (рис. 2.). если  - есть падающие и рассеиваемые волны на граничных сечениях четырехполюсника и - есть падающие и рассеиваемые волны на граничных сечениях четырехполюсника и  - соответствующие волны в сечениях генератора и нагрузки, то имеют место следующие две системы уравнений, связывающих эти величины: - соответствующие волны в сечениях генератора и нагрузки, то имеют место следующие две системы уравнений, связывающих эти величины:
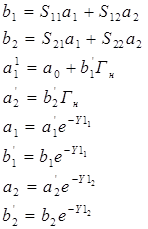 (2) (2)  (3) (3)
         
Рис. 3.
Соответствующие графы этих систем приведены на рис.3 а, б. Как видно на рис.3,а граф четырехполюсника, представленного, матрицей рассеяния [ S ] , совпадает с физической структурой системы и поэтому имеет простую интерпретацию.
С точки зрения теории графов, граф Т - матрицы получается из графа S - матрицы путем инверсии пути  . В некоторых случаях такая инверсия упрощает расчет цепи, т.к. устраняет нежелательные контуры. Примером может служить последовательное соединение четырехполюсников, коэффициент передачи которых проще рассчитывается на основе Т - матрицы. Тем не менее, учитывая известные преимущества S - матрицы, ограничим рассмотрение соответствуемыми ей графами. . В некоторых случаях такая инверсия упрощает расчет цепи, т.к. устраняет нежелательные контуры. Примером может служить последовательное соединение четырехполюсников, коэффициент передачи которых проще рассчитывается на основе Т - матрицы. Тем не менее, учитывая известные преимущества S - матрицы, ограничим рассмотрение соответствуемыми ей графами.
Связь между падающими и прошедшими волнами для шестиполюсника описывается следующей системой алгебраических уравнений:
 (4) (4)
Этой системе уравнений соответствует граф, приведенный на рис. 4. Анализируя этот граф, нетрудно установить некоторые закономерности его построения, на основании которых можно построить любой 2х - полюсник, не записывая соответствующую систему уравнений.
Действительно:
1) все а - источники, b - стоки;
2) из каждого узла а идут ветви к каждому узлу b ;
3) передача ветвей  есть коэффициент матрицы рассеяния есть коэффициент матрицы рассеяния  ; ;
4) узлы а так же, как и b ,непосредственной связи между собой не имеют.
Располагая а и b попарно ( по полюсам ) и а напротив b, получаем граф, структура которого совпадает с физической структурой распространения волн в рассматриваемом многополюснике.
Рис. 4
Если шестиполюсник нагружен отражающими нагрузками с коэффициентами отражения 

то все узлы становятся зависимыми. Фактически это означает, что стоки b имеют утечку энергии за счет отражения. Генератор - источник энергии включается в любой а - узел, а индикатор - в b - узел.
Рассмотрим несколько примеров построения графов измерительных систем.
Рис. 5

На рис.5, а приведен граф рефлектометра - двух последовательно соединенных направленных ответвителей, из которых один, ближний к нагрузке, настроен на выделение отраженной волны, а второй падающей. Сигналы  , поступающие на вход индикаторных устройств, являются очень сложными функциями всех параметров системы, в том числе измеряемого параметра , поступающие на вход индикаторных устройств, являются очень сложными функциями всех параметров системы, в том числе измеряемого параметра  . Знание этих функций позволяет наиболее правильно выбрать способ уменьшения влияния остаточных параметров и оценить остаточные погрешности. На рис.5, б приведен граф идеального рефлектометра, в котором остаточные параметры отсутствуют. . Знание этих функций позволяет наиболее правильно выбрать способ уменьшения влияния остаточных параметров и оценить остаточные погрешности. На рис.5, б приведен граф идеального рефлектометра, в котором остаточные параметры отсутствуют.
Рис. 6
На рис.6 показан граф измерительной линии, в котором x
и y
- независимые переменные, связанные соотношением х + у =
const
,
а  , ,  - входные матрицы и матрица элементов связи, на рис.7 приведен граф резонансного измерителя параметров четырехполюсников с малыми потерями, где х
и у
- независимые переменные. - входные матрицы и матрица элементов связи, на рис.7 приведен граф резонансного измерителя параметров четырехполюсников с малыми потерями, где х
и у
- независимые переменные.
Графы сложных устройств и их отдельных частей могут быть составлены на основании блок - схем этих устройств. Например, на рис. 8 дана блок - схема высокочастотной части гетеродинного измерителя ослабления и фазы коэффициента передачи с использованием направленных ответвителей для смещения сигналов. Граф этой схемы ( рис. 9 ) составлен на основе соединения графов четырехполюсников и шестиполюсников.
Рис. 7
[ S ] - матрица измеряемого элемента
Рис. 8 1 - измерительное устройство;
             2, 3 - направленные ответвители; 2, 3 - направленные ответвители;
        4, 5 - тройники с развилками. 4, 5 - тройники с развилками.
      Рассмотренные графы линейных систем могут быть распространены и на нелинейные системы. Примером может служить диод с фильтром нижних частот, включенный в измерительную схему. Если характеристика диода описывается уравнением Рассмотренные графы линейных систем могут быть распространены и на нелинейные системы. Примером может служить диод с фильтром нижних частот, включенный в измерительную схему. Если характеристика диода описывается уравнением
 , ,
то, представив это уравнение в виде
 , ,
можно сопоставить ему граф, по структуре совпадающий с линейным графом, но имеющий нелинейный коэффициент передачи.
   Рис. 9 Рис. 9           - матрицы рассеяния - матрицы рассеяния
    измеряемого устройства, измеряемого устройства,
     направленных ответвителей направленных ответвителей  и тройников в соответствии и тройников в соответствии

с рис. 8
3. Расчет цепей на основе направленных графов
Для расчетов сложных цепей, содержащих нелинейные элементы, данный граф цепи необходимо разбить на линейные подграфы. На рис. 10 показан общий случай такого разбиения. Необходимым условием правильного разбиения является отсутствие обратных связей между подграфами. Если  - матрицы передач между выходными и входными узлами соответствующих подграфов, а - матрицы передач между выходными и входными узлами соответствующих подграфов, а  - матрицы - столбцы передачи нелинейных ветвей, то матрица передач измерительной системы - матрицы - столбцы передачи нелинейных ветвей, то матрица передач измерительной системы  при воздействии на входе системы источников при воздействии на входе системы источников  равна. равна.
 (5) (5)
где l - число линейных подграфов, а показания индикаторного прибора  равны равны
 (6) (6)
Примером сложного графа с несколькими линейными подграфами может служить система с многократным преобразованием частоты. Расчет таких систем сводится к расчету линейных подграфов и определению  на основе уравнения (5). на основе уравнения (5).
Рис. 10
Графы сложных линейных систем могут быть также разбиты на подграфы. Критерии разбиения разнообразны - наличие симметрии, последовательно или параллельно соединенных четырехполюсников, изменение структуры и т.д.
Расчет линейных графов, т.е. определение передачи между выбранными входными м выходными узлами графа ( подграфа ), может быть проведена двумя способами: 1) непосредственным расчетом на основе правила не касающихся контуров и 2) последовательным упрощением графа на основе известных правил преобразования.
Правило не касающихся контуров, впервые предложенное Мэзоном / 1 /, удобно при расчете сравнительно не сложных цепей . в формулировке автора оно выражается следующим образом:
 , (7) , (7)
где  - величина k-го пути между узлами - величина k-го пути между узлами  ; ;
D - определитель графа;
D k - определитель части графа, не касающегося k-го пути, т.е. не имеющего с k-ым путем общих узлов.
Уравнение (7) может быть представлено в удобном для практического использования виде:
 (8) (8)
где  - все контуры графа ( m = 1, 2, ..... n ), - все контуры графа ( m = 1, 2, ..... n ),
причем

если путь  и контур и контур  имеет хотя бы один общий узел. имеет хотя бы один общий узел.
Практика показывает, что произведение контуров второго и более высоких порядков мало влияют на величину передачи и в большинстве случаев могут не учитываться.
При этом правило Мэзона имеет простую форму и легко применимо для нахождения зависимости между двумя любыми переменными в графе.
Рассмотрим пример - направленный ответвитель, к плечам которого подключены генератор, нагрузка и индикатор ( рис.11, а ). Передача между узлами  в соответствии с уравнением (8) равна в соответствии с уравнением (8) равна
 (9) (9)
Как видно из уравнения (9), даже простая система приводит к сравнительно сложному выражению для передачи, требующему каких-то упрощений для практического использования. Для упрощения подобных графов удобно воспользоваться условием зависимости и устранить ветви, не имеющие ни какой информации ( например,  ). Эта операция может быть проведена понижением порядка графа - устранением вершины ). Эта операция может быть проведена понижением порядка графа - устранением вершины  . Для этого выделяем связи, имеющие непосредственный интерес и не проходящие через вершину . Для этого выделяем связи, имеющие непосредственный интерес и не проходящие через вершину  ( рис.11, б ). ( рис.11, б ).
 (10) (10)
Связи  для наглядности структуры графа удобно сохранить в отдельности, несмотря на их равенство. Теперь для преобразованного графа сигнал для наглядности структуры графа удобно сохранить в отдельности, несмотря на их равенство. Теперь для преобразованного графа сигнал  равен: равен:
 (11) (11)
Наложим условие, необходимое для направленного ответвления отраженного от нагрузки сигнала
 (12 ) (12 )
Тогда в режиме выделения отраженного сигнала имеем
Рис. 11
 (14) (14)
Рассмотренный пример показывает удобство преобразования исходной структуры графа к более простому виду, сохраняя при этом общность с физической структурой системы и используя обобщенные параметры  , доступные экспериментальному определению. Критериями упрощения являются выделение основных связей и устранение второстепенных, являющихся в процессе эксперимента постоянными. Узлы, которые при измерительных манипуляциях получают связи с другими узлами, исключать при преобразовании нельзя. Практически наиболее часто упрощаются части графа, имеющие непосредственные связи с индикаторным каналом, как и в рассмотренном выше случае. , доступные экспериментальному определению. Критериями упрощения являются выделение основных связей и устранение второстепенных, являющихся в процессе эксперимента постоянными. Узлы, которые при измерительных манипуляциях получают связи с другими узлами, исключать при преобразовании нельзя. Практически наиболее часто упрощаются части графа, имеющие непосредственные связи с индикаторным каналом, как и в рассмотренном выше случае.
На рис. 12, а представлен граф восьмиполюсника, к плечам 1 и 2 которого подключены генератор и нагрузка соответственно, а к плечам 3 и 4 - индикаторы. Пользуясь описанным выше примером, приведем этот граф к виду, показанному на рис. 12, б. Передачи ветвей преобразованного графа есть следующие функции передач ветвей основного графа:
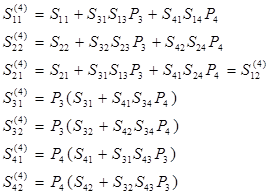 (15) (15)
где  - передачи контуров индикаторных плеч - передачи контуров индикаторных плеч
 (16) (16)
Преобразованный граф ( рис. 12, б ) - это граф с односторонними связями с индикаторными плечами, что является удобным для практического анализа. Реакции индикаторных плеч на остальную схему учитывается в передачах преобразованного графа.
Для общего случая 2n - полюсника, в котором (n - k) индикаторных плеч упрощаются к рассмотренным выше односторонним связям, могут быть получены следующие рекуррентные формулы. Для связей в не индикаторных плечах:
 (17) (17)
Для связей между неиндикаторными плечами:
 (18) (18)
Для связей индикаторных с неиндикаторными плечами:
 (19) (19)
Рассмотрим другой вид преобразования, имеющий практический интерес и выполненный методами алгебраических матриц значительно сложнее - 2n - полюсника.
Преобразуем нагруженный восьмиполюсник ( рис. 12, а ) к шестиполюснику путем исключения связей с индексом «4». При этом передача каждой ветви получаемого шестиполюсника есть сумма передач соответствующей ветви восьмиполюсника плюс величина пути между рассматриваемыми узлами, проходящие через исключаемые узлы 4 и 4’.
Пользуясь этим простым правилом, получим
 (20) (20)
На основании формул (20) нетрудно получить рекуррентную формулу для преобразования 2n - полюсника в 2(n -1) - полюсник:
 (21) (21)
Производя дальнейшее понижение порядка 2n - полюсника до 2(n - k) - полюсника, аналогично можно получить общую рекуррентную формулу
 (22) (22)
Формулы (21) и (22) могут быть получены алгебраическим путем - понижением порядка матрицы, что соответствует исключению узлов графа, однако эта процедура несравненно сложнее, что наглядно показывает преимущество топологического представления перед алгебраическим матричным.
Список используемой литературы
1. Мэзон С., Циммерман Г. Электронные цепи, сигналы и системы. ИЛ,1963.
2. Берж К. Теория графов и ее применение. ИЛ, 1962.
3. Абрахамс Дж., Каверли Дж. Анализ электрических цепей методом графов. Изд-во «Мир», 1967.
4. Заездный А.М., Гуревич И.В. Основы расчетов радиотехнических цепей. Изд. 2-е, М., «Связь», 1968.
5. Хантон Дж. Анализ микроволновых цепей посредством графов потока сигналов. IEEE Traus on Microwave Theory and Tech. MTT-8, № 2, 1960.
6. Петров В.П. Радиотехнические цепи. М., «Связь», 1989.
Список обозначений
 - комплексный коэффициент отражения; - комплексный коэффициент отражения;
 - коэффициенты матрицы рассеяния; - коэффициенты матрицы рассеяния;
Y = a + jb - постоянная распространения;
 - волновое сопротивление; - волновое сопротивление;
КСВ - коэффициент стоячей волны;
z = r + j x - комплексное сопротивление;
y = g + j b - комплексная проводимость;
Z = R + j X - комплексное нормированное сопротивление;
Y = G + j B - комплексная нормированная проводимость;
l - длина волны;
f - частота;
w = 2pf - круговая частота;
Н - ослабление, дБ;
e = e’ - je’’ - комплексная диэлектрическая проницаемость;
m = m’- jm’’ - комплексная магнитная проницаемость;
Q - добротность4
D - наружный диаметр проводника;
d - внутренний диаметр проводника.
Применяемые индексы
вх - вход;
вых - выход;
г - генератор;
н - нагрузка;
1, 2, 3.... - при Г, Z, Y относятся к сечениям 1-1’; 2-2’; 3-3’...... ;
‘0 - начальное значение;
max - максимальный;
min - минимальный;
пад - падающая волна;
отр - отраженная волна;
хх - холостой ход;
кз - короткое замыкание.
|