| Федеральное агентство по образованию Российской Федерации
Южно-Уральский государственный университет
Кафедра «Системы электроснабжения»
Курсовая работа
по курсу «Переходные процессы в электрических системах»
Э-468.1004.035.00.00 ПЗ
Нормоконтролер
Столбов Ю.А.
«__»________2006 г.
Руководитель
Столбов Ю.А.
«__»________2006 г.
Автор проекта
студент группы Э–468
Павлов Е.В.
«__»________2006 г.
Проект защищен с оценкой
________________
«__»________2006 г.
Челябинск
2006
Задание
Генераторная станция работает на шины бесконечной мощности через две параллельные линии 2хАС-F
и передает мощность  при при  (рис. 1). Напряжение на шинах приемной системы поддерживается неизменным, равным (рис. 1). Напряжение на шинах приемной системы поддерживается неизменным, равным  . Генераторы оснащены системой АРВ пропорционального действия. . Генераторы оснащены системой АРВ пропорционального действия.
Рисунок 1. Схема системы
1. Используя постоянные четырехполюсника, построить круговые диаграммы и угловые характеристики передачи при условии поддержания неизменным тока возбуждения генератора.
2. Построить статическую  и динамическую и динамическую  угловые характеристики генераторной станции и определить коэффициент запаса статической устойчивости для каждой из характеристик при угле угловые характеристики генераторной станции и определить коэффициент запаса статической устойчивости для каждой из характеристик при угле  , соответствующем передаваемой мощности , соответствующем передаваемой мощности  . .
3. Выявить влияние коэффициента мощности нагрузки  на запас статической устойчивости системы при условии поддержания неизменной величины передаваемой активной мощности на запас статической устойчивости системы при условии поддержания неизменной величины передаваемой активной мощности  . .
4. Проверить статическую устойчивость системы без учета действия АРВ, найти частоту и период собственных колебаний в различных режимах без учета и с учетом демпферного момента. Определить зависимость изменения угла во времени при отклонении ротора на один градус от положения установившегося режима при  ; ;  ; ;  и и  . .
5. По заданной принципиальной электрической схеме системы АРВ составить структурную схему электрической системы с АРВ пропорционального действия.
6. Последовательными преобразованиями упростить структурную схему и определить эквивалентную передаточную функцию системы, а также характеристический многочлен системы с учетом наличия АРВ пропорционального действия.
7. Произвести анализ устойчивости системы по алгебраическому критерию Гурвица и частотному критерию Михайлова.
8. Используя D-разбиения, найти область допустимых значений параметра системы АРВ пропорционального действия –  . .
9. Произвести расчет динамической устойчивости системы с определением предельного угла отключения аварии при двухполюсном коротком замыкании на землю одной из параллельных линий вблизи шин генераторной станции.
Вариант курсового проекта № 35. Исходные данные занесены в
таблицу 1.
Таблица 1
| № вар.
|
Расчетные данные
|
|  , кВ , кВ
|
 , МВт , МВт
|
 , км , км
|
 , МВт , МВт
|
 , с , с
|
 , с , с
|
 , с , с
|

|
| 35
|
320
|
484
|
510
|
2 х 300
|
10
|
2,0
|
4,0
|
83
|
| 
|

|

|
 , МВА , МВА
|
 ,% ,%
|
 ,% ,%
|
 ,о.е. ,о.е.
|
| 0,85
|
2,0
|
0,3
|
2 х 400
|
2
|
10,5
|
30
|
Аннотация
Павлов Е.В. Исследование статической и динамической устойчивости простейшей регулируемой системы, состоящей из генераторной станции, работающей на шины бесконечной мощности через две параллельные линии
электропередачи. – Челябинск: ЮУрГУ, Э, 2006.
58 с. 28 илл. Библиография литературы – 3 наименования.
Данная курсовая работа посвящена исследованию статической и динамической устойчивости регулируемой системы, включающей в себя генераторную станцию, работающей на шины бесконечной мощности через две параллельные линии электропередачи.
Содержание
1. Определение параметров схемы замещения и построение круговых диаграмм и угловых характеристик передачи. 6
2. Построение статической  и динамической и динамической  угловых характеристик генераторной станции и определение коэффициента запаса статической устойчивости 16 угловых характеристик генераторной станции и определение коэффициента запаса статической устойчивости 16
3. Влияние коэффициента мощности нагрузки  на запас статической устойчивости системы.. 20 на запас статической устойчивости системы.. 20
4. Проверка статической устойчивости системы без учета действия АРВ и определение зависимости изменения угла во времени. 22
5. Структурная схема электрической системы с АРВ пропорционального действия 29
6. Упрощение структурной схемы.. 34
7. Анализ устойчивости системы по алгебраическому критерию Гурвица и частотному критерию Михайлова. 40
8. Нахождение области допустимых значений параметра системы АРВ пропорционального действия –  ....... 43 ....... 43
9. Расчет динамической устойчивости системы.. 46
Заключение. 57
Литература. 58
Для определения параметров схемы замещения системы необходимо выбрать сечение линий электропередач по экономической плотности тока. При этом следует иметь ввиду, что при заданном номинальном напряжении 330 кВ провод в фазе расщепляется на два. В этом случае радиус эквивалентного провода может быть подсчитан по формуле
 , ,
где  – действительный радиус провода, мм: – действительный радиус провода, мм:
 ; ;
 – число проводов в фазе; – число проводов в фазе;
 – среднегеометрическое расстояние между проводами – среднегеометрическое расстояние между проводами
одной фазы линии (для данной линии не менее 300 мм), мм.

Затем по известным из курса электрических сетей формулам определяются удельные километрические индуктивные и емкостные сопротивления передачи:

Где  - среднегеометрическое расстояние между проводами, - среднегеометрическое расстояние между проводами,  мм; мм;

Емкостная проводимость


и активное сопротивление одной цепи линий электропередачи


При составлении электрической схемы замещения системы (рис. 2), можно пренебречь активными сопротивлениями и проводимостями трансформатора.
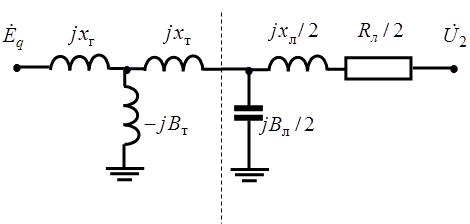
Рисунок 2. Схема замещения системы
Параметры всех элементов, входящих в схему замещения должны быть выражены в относительных единицах, приведенных к базисным условиям. Для упрощения расчетов удобно за базисную мощность принять полную мощность, передаваемую генерирующей станцией в систему бесконечной мощности  , ,

а за базисное напряжение – напряжение на шинах приемной системы  . .
 , ,
где












 , с , с
 . .
Ветвь проводимости, подсоединенная к линиям системы бесконечной мощности, исключается из схемы замещения.
Таким образом, эквивалентная схема замещения системы может быть представлена последовательным соединением двух четырехполюсников, разделенных на рис.2 вертикальной пунктирной линией, Т-образного четырехполюсника, содержащего элементы  , и Г-образного, состоящего из элементов , и Г-образного, состоящего из элементов  и и  . .
Обобщенные постоянные Т-образного четырехполюсника:








Выполним проверку:

Обобщенные постоянные Г-образного четырехполюсника:
 ; ;






Делаем проверку расчетов:

Обобщенные постоянные эквивалентного четырехполюсника (рис.3) подсчитываются по формулам



 




Рисунок 3. Эквивалентный четырехполюсник
Для системы с эквивалентными постоянными  уравнения для токов и напряжений будут представлены в виде: уравнения для токов и напряжений будут представлены в виде:

При построении круговых диаграмм вектор напряжения  в конце передачи удобно совместить с действительной осью комплексной плоскости мощностей, т.е. в конце передачи удобно совместить с действительной осью комплексной плоскости мощностей, т.е.  . Тогда . Тогда  , а ЭДС генератора будет опережать напряжение на угол нагрузки , а ЭДС генератора будет опережать напряжение на угол нагрузки  , т.е. , т.е.  . Из первого уравнения системы получаем: . Из первого уравнения системы получаем:

Тогда комплексы полных мощностей начала и конца передачи определяются выражениями:
 , ,
 . .
Таким образом, выражения для мощностей начала и конца системы представляют собой сумму двух векторов: для мощности в начале системы первый вектор  и второй и второй  . Их геометрическая сумма и дает комплекс мощности . Их геометрическая сумма и дает комплекс мощности  в начале передачи. в начале передачи.
Комплекс мощности  в конце передачи состоит из суммы векторов в конце передачи состоит из суммы векторов  и и  . .
Действительные части этих комплексов представляют собой соответственно активные мощности  и и  , а мнимые – реактивные , а мнимые – реактивные  и и  . При постоянстве ЭДС . При постоянстве ЭДС  в начале и напряжения в начале и напряжения  в конце системы единственной переменной величиной является угол в конце системы единственной переменной величиной является угол  . В этом случае комплексы . В этом случае комплексы  и и  остаются неизменными по величине и по фазе, а комплексы остаются неизменными по величине и по фазе, а комплексы  и и  , оставаясь неизменными по величине, изменяют угол поворота с изменением угла , оставаясь неизменными по величине, изменяют угол поворота с изменением угла  . При . При  они занимают положение они занимают положение   , где , где  – аргумент комплекса – аргумент комплекса  , ,  . При угле . При угле  , отличном от нуля, они поворачиваются на этот угол: для начала системы – против часовой стрелки и для конца системы – по часовой стрелке (рис. 4). , отличном от нуля, они поворачиваются на этот угол: для начала системы – против часовой стрелки и для конца системы – по часовой стрелке (рис. 4).
Из рисунка видно, что при этих условиях концы комплексов полных мощностей начала и конца перемещаются по окружностям, центры которых определяются радиус-векторами:
для мощности в начале системы


для мощности в конце системы


Радиусы обеих окружностей одинаковы:


Отсчет углов  производится от линии, проведенной из центра окружностей под углом производится от линии, проведенной из центра окружностей под углом  к горизонтали. к горизонтали.
Из характерных для четырехполюсников соотношений известно:






где  и и  – собственные, а – собственные, а  – взаимная проводимости системы. – взаимная проводимости системы.
Угловые характеристики для активных мощностей начала и конца передачи определяются по выражениям:
 , ,
 , ,
где













Рис. 4. Круговая диаграмма передачи
2
. Построение статической  и динамической и динамической  угловых характеристик генераторной станции и определение коэффициента запаса статической устойчивости угловых характеристик генераторной станции и определение коэффициента запаса статической устойчивости
При наличии у генератора автоматического регулятора пропорционального типа машина характеризуется переходным сопротивлением  , и действующей за ним переходной ЭДС , и действующей за ним переходной ЭДС  , величина которой поддерживается постоянной при изменении нагрузки. , величина которой поддерживается постоянной при изменении нагрузки.
Для качественной оценки влияния АРВ на коэффициент статической устойчивости системы рассмотрим упрощенную схему замещения сети, пренебрегая активными сопротивлениями элементов и контуром намагничивания трансформатора.
На рис.5 изображена совмещенная схема замещения системы, в которой генерирующая станция при отсутствии АРВ представлена ЭДС холостого хода  и продольной синхронной реактивностью и продольной синхронной реактивностью  , а при наличии АРВ – переходной ЭДС , а при наличии АРВ – переходной ЭДС  за переходным сопротивлением за переходным сопротивлением  . .

Рисунок 5. Совмещенная схема замещения системы

Угловая характеристика генератора при отсутствии АРВ, представленная на рис.6, построена согласно выражению
 . .
Это – так называемая статическая характеристика синхронной машины при поддержании в ней неизменного тока возбуждения ( ). ).
При изменении нагрузки, например, при ее возрастании угловая характеристика от начального угла  пойдет по другой кривой, соответствующей выражению пойдет по другой кривой, соответствующей выражению
 . .
Входящие в формулы для угловых характеристик выражения  и и  представляют собой взаимные сопротивления схемы замещения сети (рис.5) при отсутствии и наличии у генераторов АРВ соответственно: представляют собой взаимные сопротивления схемы замещения сети (рис.5) при отсутствии и наличии у генераторов АРВ соответственно:




Угловая характеристика  представляет собой динамическую характеристику генератора и имеет место только в переходном режиме, т.е. в процессе изменения передаваемой мощности. Началом динамической характеристики является предшествующий изменению передаваемой мощности установившийся режим, соответствующий углу представляет собой динамическую характеристику генератора и имеет место только в переходном режиме, т.е. в процессе изменения передаваемой мощности. Началом динамической характеристики является предшествующий изменению передаваемой мощности установившийся режим, соответствующий углу  на статической характеристике на статической характеристике  . Естественно, что при этом угле статическая и динамическая характеристики будут иметь общую точку, т.е. . Естественно, что при этом угле статическая и динамическая характеристики будут иметь общую точку, т.е.  при при  , (рис.6). Если сравнить амплитуды угловых характеристик мощностей, полученных при постоянстве , (рис.6). Если сравнить амплитуды угловых характеристик мощностей, полученных при постоянстве  и и  , то нетрудно заметить, что амплитуда динамической угловой характеристики значительно превышает амплитуду статической характеристики и, кроме того, максимум динамической угловой характеристики смещается вправо и превышает угол , то нетрудно заметить, что амплитуда динамической угловой характеристики значительно превышает амплитуду статической характеристики и, кроме того, максимум динамической угловой характеристики смещается вправо и превышает угол  , соответствующий статическому пределу мощности нерегулируемой системы. , соответствующий статическому пределу мощности нерегулируемой системы.
Необходимые для построения угловых характеристик значения ЭДС  и и  можно определить по векторной диаграмме системы (рис.7) по следующим соотношениям: можно определить по векторной диаграмме системы (рис.7) по следующим соотношениям:




Переходная ЭДС  равна проекции вектора ЭДС равна проекции вектора ЭДС  на поперечную ось машины на поперечную ось машины  : :


Рисунок 6. Векторная диаграмма системы
Если сравнить амплитуды угловых характеристик мощностей, полученных при постоянстве  и и  , то нетрудно заметить, что коэффициент статической устойчивости , то нетрудно заметить, что коэффициент статической устойчивости  значительно превышает коэффициент статической устойчивости значительно превышает коэффициент статической устойчивости  . .





Рисунок 7. Статическая и динамическая характеристики генератора
На величину предела передаваемой мощности весьма сильное влияние оказывает коэффициент мощности нагрузки. Чем меньше коэффициент мощности нагрузки при нормальном режиме работы, тем больше должна быть ЭДС генератора при заданном напряжении в конце системы  и следовательно, тем выше будет предел передаваемой мощности (рис. 8). и следовательно, тем выше будет предел передаваемой мощности (рис. 8).
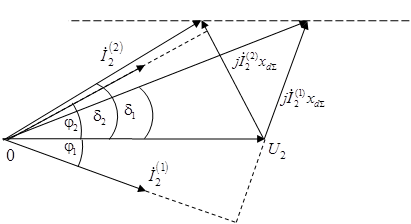
Рисунок 8. Зависимость ЭДС генератора от коэффициента мощности
Площадь треугольника  пропорциональна активной мощности, задаваемой генераторной станцией. Тогда при изменении коэффициента мощности нагрузки и поддержании неизменной величины передаваемой активной мощности пропорциональна активной мощности, задаваемой генераторной станцией. Тогда при изменении коэффициента мощности нагрузки и поддержании неизменной величины передаваемой активной мощности  конец вектора ЭДС конец вектора ЭДС  будет скользить по прямой, параллельной вектору напряжения системы будет скользить по прямой, параллельной вектору напряжения системы  . .
Для выявления указанной зависимости расчет коэффициента статической устойчивости системы произвести для следующих значений  : :  в индуктивном и емкостном квадрантах работы генератора. в индуктивном и емкостном квадрантах работы генератора.
При этом рекомендуется следующая последовательность расчета:
1. Для заданного коэффициента мощности  нагрузки определяется величина и фаза тока нагрузки определяется величина и фаза тока  ; причем для отстающего тока в индуктивном квадранте берется знак «-», а для опережающего тока, соответствующего емкостному квадранту, – знак «+
». ; причем для отстающего тока в индуктивном квадранте берется знак «-», а для опережающего тока, соответствующего емкостному квадранту, – знак «+
».
2. По формуле  определяется ЭДС определяется ЭДС  , соответствующая рассматриваемому коэффициенту мощности. , соответствующая рассматриваемому коэффициенту мощности.
3. Рассчитывается коэффициент статической устойчивости системы по формуле  . .
Результаты расчетов сводим в таблицу 2.
Таблица 2.
| Квадрант
|

|

|

|

|
| Емкостный
|

|

|

|

|
| 
|

|

|

|
| 
|

|

|

|
| 
|

|

|

|
| Индуктивный
|

|

|

|

|
| 
|

|

|

|
| 
|

|

|

|
Построим зависимость  (рис. 9): (рис. 9):

Рисунок 9. Зависимость  от коэффициента мощности нагрузки от коэффициента мощности нагрузки
4.
Проверка статической устойчивости системы без учета действия АРВ и определение зависимости изменения угла во времени
Проверка статической устойчивости нерегулируемой системы (без учета действия АРВ) заключается в исследовании уравнения движения ротора машины:
 , ,
которое после линеаризации принимает вид:
 , ,
где
 – синхронизирующая мощность в окрестности угла – синхронизирующая мощность в окрестности угла  . .
Здесь и в дальнейшем будем пренебрегать активными сопротивлениями системы, а также реактивной проводимостью трансформатора ввиду малости их значений. Тогда величина результирующего сопротивления системы будет равна взаимному сопротивлению, найденному из упрощенной схемы передачи, изображенной на рис. 10:
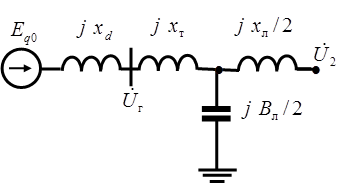
Рисунок 10. Упрощенная схема замещения нерегулируемой системы


Сначала рассмотрим так называемую консервативную систему, в которой отсутствует обмен энергии с окружающей средой, что будет соответствовать равенству нулю демпферного момента ( ) в уравнении движения ротора. Определим при этом условии частоту и период колебаний ротора генератора при отклонении его на один градус для следующих начальных значений угла: ) в уравнении движения ротора. Определим при этом условии частоту и период колебаний ротора генератора при отклонении его на один градус для следующих начальных значений угла:  ; ;  ; ;  . .
Характеристическое уравнение движения ротора имеет вид
 . .
Тогда на восходящем участке угловой характеристики генератора в диапазоне рабочих углов  корни характеристического уравнения будут выражаться чисто мнимыми числами, что указывает на колебательный характер движения ротора с неизменной амплитудой. Это соответствует квазиустойчивому состоянию системы. С возрастанием рабочего угла корни характеристического уравнения будут выражаться чисто мнимыми числами, что указывает на колебательный характер движения ротора с неизменной амплитудой. Это соответствует квазиустойчивому состоянию системы. С возрастанием рабочего угла  будет также возрастать и период колебания ротора, определяемый корнями характеристического уравнения будет также возрастать и период колебания ротора, определяемый корнями характеристического уравнения
 . .
Частота колебаний может быть выражена либо в  , либо в , либо в  : :
 , ,
 . .
Период колебаний – это величина, обратная частоте
 . .
Тогда решение уравнения движения ротора имеет вид
 . .
При работе на нисходящем участке угловой характеристики, что соответствует углам  больше больше  , синхронизирующая мощность будет отрицательна, и один из корней характеристического уравнения будет выражен действительным положительным числом, что соответствует неустойчивому состоянию системы. , синхронизирующая мощность будет отрицательна, и один из корней характеристического уравнения будет выражен действительным положительным числом, что соответствует неустойчивому состоянию системы.
Проведем вычисления и занесем их в таблицу 3, а кривые, иллюстрирующие движение ротора генератора при этих условиях представим на рис. 11.
Таблица 3
| 
|

|

|

|

|

|
| 
|
1,132
|
5,521
|
 j 5,521 j 5,521
|
0,879
|
1,138
|
| 
|
0,887
|
4,886
|
 j 4,886 j 4,886
|
0,778
|
1,286
|
| 
|
-0,478
|
j 3,589
|
 j 3,589 j 3,589
|
j 0,571
|
-j 1,751
|

Рисунок 11. Изменение приращения угла  при при  : :
кривая 1 для  ; ;
кривая 2 для  ; ;
кривая 3 для 
При учете демпферного момента корни определяются из следующего характеристического уравнения:
 , ,
 . .
Решение линеаризованного уравнения второго порядка имеет вид
 . .
Постоянные интегрирования  и и  определяются из начальных условий: определяются из начальных условий:
 ; ;
 . .
Решив совместно эти два уравнения, можно определить искомые постоянные:
 , ,
 . .
Таким образом,
 . .
Из курса теории автоматического управления известно, что необходимым и достаточным признаком устойчивости линейной системы второго порядка является положительность всех коэффициентов ее характеристического уравнения. В этом случае возврат системы к прежнему состоянию при отклонении одного или нескольких определяющих параметров будет происходить либо по периодическому закону с затухающей амплитудой, либо по затухающей экспоненте.
Известно, что колебательный процесс возникает при наличии комплексно-сопряженных корней характеристического уравнения. Этот режим возможен при сравнительно малых углах  и, соответственно, значительных величинах синхронизирующей мощности и, соответственно, значительных величинах синхронизирующей мощности  . Тогда в выражениях для корней характеристического уравнения вычитаемое под знаком радикала по абсолютной величине будет больше уменьшаемого, и корни выражаются комплексно-сопряженными числами: . Тогда в выражениях для корней характеристического уравнения вычитаемое под знаком радикала по абсолютной величине будет больше уменьшаемого, и корни выражаются комплексно-сопряженными числами:
 , ,
где
 – декремент затухания амплитуды колебаний: – декремент затухания амплитуды колебаний:

 – частота колебаний. – частота колебаний.
Увеличение угла нагрузки генератора  будет сопровождаться уменьшением величины синхронизирующей мощности будет сопровождаться уменьшением величины синхронизирующей мощности  , и при определенных условиях подкоренное выражение обращается в нуль. Угол , и при определенных условиях подкоренное выражение обращается в нуль. Угол  , при котором наступает это равенство, носит название граничного угла и может быть подсчитан по формуле: , при котором наступает это равенство, носит название граничного угла и может быть подсчитан по формуле:
 , где , где  , ,
Тогда величина граничного угла определяется выражением


При значениях угла  процесс носит колебательный характер, а в диапазоне процесс носит колебательный характер, а в диапазоне  процесс будет носить апериодический характер, так как в этом случае оба корня характеристического уравнения выражаются отрицательными действительными числами. процесс будет носить апериодический характер, так как в этом случае оба корня характеристического уравнения выражаются отрицательными действительными числами.
При достижении углами нагрузки значений больше  синхронизирующая мощность синхронизирующая мощность  становится отрицательной, что приводит к появлению корня, выраженного действительным положительным числом, и система теряет устойчивость. становится отрицательной, что приводит к появлению корня, выраженного действительным положительным числом, и система теряет устойчивость.
Для всех рассмотренных режимов по вышеприведенным формулам был проведен расчет, результаты которого занесены в таблицу 4, а зависимости  представлены на графиках (рис. 12). представлены на графиках (рис. 12).
Таблица 4
| 
|

|

|

|
| 
|
1,132
|
-1,286+j 5,369
|
-1,286-j 5,369
|
| 
|
0,887
|
-1,286+j 4,714
|
-1,286-j 4,714
|
| 

|
0,04
|
-0,518
|
-2,053
|
| 
|
-0,478
|
2,527
|
-5,098
|
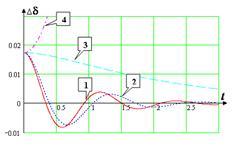
Рисунок 12. Колебания ротора синхронного генератора при  : :
кривая 1 для  ; ;
кривая 2 для  ; ;
кривая 3 для  ; ;
кривая 4 для  . .
5.
Структурная схема электрической системы с АРВ пропорционального действия
При исследовании статической устойчивости системы с учетом автоматического регулятора пропорционального действия, установленного на генераторной станции, необходимо принципиальной схеме с АРВ, представленной на рис. 13, сопоставить структурную схему.
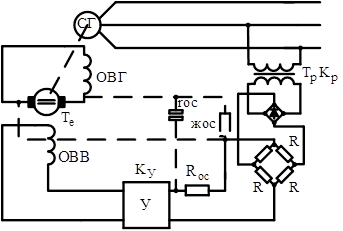
Рисунок 13. Принципиальная схема АРВ пропорционального действия
Для упрощения исследования в структурной схеме, изображенной на рис. 14, исключено инерционное звено с постоянной времени  , которую можно положить равной нулю ввиду ее малости. Это понижает на единицу порядок характеристического уравнения системы. , которую можно положить равной нулю ввиду ее малости. Это понижает на единицу порядок характеристического уравнения системы.
Поясним принцип составления структурной схемы.
Для проведения качественного анализа статической устойчивости системы можно пренебречь также демпферным моментом в уравнении движения ротора, т.е. принять  : :
 (1) (1)
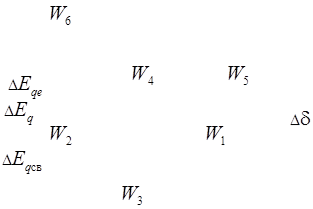 
Рисунок 14. Структурная схема системы с АРВ
Второе уравнение, учитывающее электромагнитный переходный процесс в обмотке возбуждения, имеет вид
 . (2) . (2)
ЭДС  генератора может рассматриваться как выходная функция входной величины генератора может рассматриваться как выходная функция входной величины  , (рис. 15). , (рис. 15).

Рисунок 15. Функциональная зависимость 
 или с учетом того, что или с учетом того, что  , а произведение , а произведение  – коэффициент усиления системы, получим – коэффициент усиления системы, получим
 . (3) . (3)
Линеаризуем исходные уравнения (1) и (2) движения системы.
При этом следует иметь ввиду, что каждая из раскладываемых по первому приближению в ряд Тейлора функций является функцией двух переменных – угла  и ЭДС и ЭДС  : :
 . .
Тогда уравнению (1) будет соответствовать линеаризованное уравнение
 , (4) , (4)
где
 , ,
 . .
Уравнение (2) перепишем в виде

и разложим в ряд Тейлора:
 . .
С учетом (3) получим выражение для приращения ЭДС  : :
  . .
В последнем выражении выделим составляющие, обусловленные действием АРВ, и составляющие, обусловленные электромагнитным переходным процессом.
Так как,  , а , а  , ,
то
 , (5) , (5)
где принужденная составляющая приращения ЭДС  , обусловленная действием АРВ, , обусловленная действием АРВ,
 . (6) . (6)
Уравнения (4), (5) и (6) позволяют построить структурную схему системы, изображенную на рис. 14. Для этого уравнение (4), положив в нем  выходным сигналом, а выходным сигналом, а  – выходным, удобно переписать в следующем виде: – выходным, удобно переписать в следующем виде:

или
 , ,
где
 – передаточная функция колебательного звена; – передаточная функция колебательного звена;
 – передаточная функция усилительного звена – передаточная функция усилительного звена
с отрицательным коэффициентом усиления.
Сложив последовательно эти звенья, получаем звено  , передаточная функция которого , передаточная функция которого
 . .
Таким образом, входная величина  складывается из свободной составляющей, обусловленной электромагнитным переходным процессом в роторе складывается из свободной составляющей, обусловленной электромагнитным переходным процессом в роторе  и принужденной составляющей и принужденной составляющей  , определяемой действием АРВ. , определяемой действием АРВ.
Поэтому в структурной схеме должно появиться звено  и сумматор, на вход которого подаются и сумматор, на вход которого подаются  и и  . Физически сумматор соответствует напряжению на кольцах ротора. Это напряжение подается далее на обмотку возбуждения, обладающую значительной индуктивностью, и поэтому в структурной схеме она должна быть представлена инерционным звеном с передаточной функцией . Физически сумматор соответствует напряжению на кольцах ротора. Это напряжение подается далее на обмотку возбуждения, обладающую значительной индуктивностью, и поэтому в структурной схеме она должна быть представлена инерционным звеном с передаточной функцией  . .
Определяемая выражением (6) принужденная ЭДС суммируется из двух составляющих приращений напряжения – по углу и по ЭДС. Поэтому на структурной схеме необходимо показать еще один сумматор, на вход которого поступают выходные величины звеньев  и и  . .
В соответствии с уравнением (6) эта сумма поступает на вход инерционного звена  , представляющего собой последовательно соединенные звенья , представляющего собой последовательно соединенные звенья  и и  , (рис. 15). Его передаточная функция имеет вид , (рис. 15). Его передаточная функция имеет вид
 . .
Как видно из структурной схемы, система АРВ отражается внешней обратной связью по отношению к объекту регулирования.
6. У
прощение структурной схемы
Последовательными преобразованиями структурная схема системы упрощается до одного направленного звена, знаменатель передаточной функции которого и будет представлять характеристическое уравнение регулируемой системы.
Сначала переносится узел за звено  , (рис. 16). , (рис. 16).
         
Рисунок 16. Поэтапное преобразование структурной схемы
Складываем последовательно звенья  с с  и и  с с 
 , ,
 . .
Складывая параллельно два звена  и и  , получаем , получаем
 . .
При сложении последовательно последней функции с  получаем звено с передаточной функцией получаем звено с передаточной функцией  : :
 , ,
 , ,
 . .
Таким образом, структурная схема системы после всех приведенных выше преобразований принимает вид, показанный на рис. 17.
     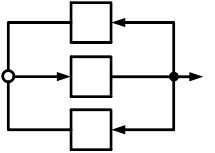
Рисунок 17. Структурная схема системы после преобразований
Если звено  является звеном обратной связи по отношению к является звеном обратной связи по отношению к  , тогда , тогда
 . .
Выражение для передаточной функции эквивалентного направленного звена системы в целом
 . .
Знаменатель передаточной функции  представляет собой характеристический многочлен системы с АРВ пропорционального действия, который после подстановки выражений для представляет собой характеристический многочлен системы с АРВ пропорционального действия, который после подстановки выражений для  , ,  , ,  и записи его по убывающим степеням и записи его по убывающим степеням  принимает вид принимает вид

Общая форма записи характеристического уравнения движения системы  -го порядка записывается в виде -го порядка записывается в виде
 . .
Для расчета коэффициентов уравнения определяются сопротивления в соответствии со схемой замещения системы, представленной на рис. 18:
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 . .
Тогда напряжения источников ЭДС, приведенных в схеме (рис.18), определяются из очевидных соотношений:
 ; ;
 ; ;
;
 ; ;

Рисунок 18. Схема замещения системы, поясняющая принцип определение частных производных
Значение переходной ЭДС  определится как проекция ЭДС определится как проекция ЭДС  на поперечную ось генератора на поперечную ось генератора  : :
 ; ;
 . .
Напряжение на выводах генератора  определяется аналогично: определяется аналогично:
 ; ;
 . .
Величина угла
 ; ;
 . .
ся частными производными угловых характеристик простейшей системы. Их аналитические выражения:
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;

Так как рассматриваемая система – система четвертого порядка, то
 ; ;  ; ;
 ; ;
 ; ;
 , ,
Для соблюдения размерностей при расчете коэффициентов  характеристического уравнения постоянные времени характеристического уравнения постоянные времени  и и  подставляются в секундах, а постоянная инерции при подстановке ее значения подставляются в секундах, а постоянная инерции при подстановке ее значения  в секундах должна быть поделена на в секундах должна быть поделена на  . .
 ; ;
 ; ;
 ; ;
 ; ;
 . .
Коэффициенты  и и  целесообразно представить в виде двух слагаемых целесообразно представить в виде двух слагаемых
 и и  . .
ставляющие  и и  , содержащие коэффициент усиления системы, в большой степени влияют на величину коэффициентов характеристического уравнения и, тем самым, на устойчивость системы. , содержащие коэффициент усиления системы, в большой степени влияют на величину коэффициентов характеристического уравнения и, тем самым, на устойчивость системы.
 ; ;
 ; ;
 ; ;
 . .
7.
Анализ устойчивости системы по алгебраическому критерию Гурвица и частотному критерию Михайлова
После вычисления коэффициентов характеристического уравнения заполняется квадратная табличка-матрица для определения устойчивости системы по алгебраическому критерию Гурвица:
 . .
Так как рассматриваемое характеристическое уравнение имеет четвертый порядок, то единственным нетривиальным условием, определяющим устойчивое состояние системы, будет положительность предпоследнего определителя:
 . .

Из отрицательности предпоследнего определителя делаем вывод о неустойчивости системы. Определим нижний и верхний пределы, в которых должна лежать величина коэффициента усиления  при обеспечении устойчивости системы. при обеспечении устойчивости системы.
Нижний предел определяется из условия нахождения коэффициента  на грани нарушения тривиального условия, т.е. на грани нарушения тривиального условия, т.е.  , откуда , откуда
 . (7) . (7)

Верхний предел коэффициента усиления  находится из условия находится из условия  : :
 (8) (8)
 . .
Для систем более высокого порядка использование алгебраического критерия Гурвица превращается в весьма громоздкую операцию и затрудняет оценку параметров системы на ее устойчивость. Поэтому большой интерес представляет предложенный А.В. Михайловым достаточно простой, удобный и наглядный графоаналитический критерий устойчивости.
В данном случае рассматриваемое уравнение четвертого порядка
 . .
Обозначив характеристический многочлен, находящийся в его левой части, через  , получим , получим
 . .
Подставим теперь в это выражение  вместо вместо  . При этом . При этом  в общем случае не равно нулю, если только в общем случае не равно нулю, если только  не является корнем рассматриваемого уравнения. В этом случае не является корнем рассматриваемого уравнения. В этом случае
 , ,
где
 (9) (9)

Величина  является комплексным числом, которое может быть изображено на комплексной плоскости. Если теперь начать изменять параметр является комплексным числом, которое может быть изображено на комплексной плоскости. Если теперь начать изменять параметр  от от  до до  , то конец вектора , то конец вектора  опишет на комплексной плоскости некоторую кривую, которая называется кривой Михайлова, являющейся годографом вектора опишет на комплексной плоскости некоторую кривую, которая называется кривой Михайлова, являющейся годографом вектора  при при  и дающей ответ об устойчивости системы. и дающей ответ об устойчивости системы.
Формулировка критерия устойчивости Михайлова такова.
Если результирующий угол поворота вектора  при изменении при изменении  от от  до до  равен равен  , то система устойчива. Если же этот угол отличается от , то система устойчива. Если же этот угол отличается от  , то система неустойчива. При этом за положительный угол поворота считается направление против часовой стрелки. Для уравнения четвертой степени в устойчивой системе конец вектора , то система неустойчива. При этом за положительный угол поворота считается направление против часовой стрелки. Для уравнения четвертой степени в устойчивой системе конец вектора  должен повернуться вокруг начала системы координат на результирующий угол должен повернуться вокруг начала системы координат на результирующий угол  и описать годограф. Таким образом, для найденного и описать годограф. Таким образом, для найденного  получаем годограф следующего вида (рис.19). получаем годограф следующего вида (рис.19).
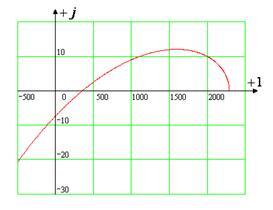
Рисунок 19. Годограф Михайлова
Полученная кривая не удовлетворяет исходным условиям. Таким образом, и алгебраический критерий Гурвица, и критерий Михайлова показали, что система с коэффициентом усиления регулятора  является неустойчивой. является неустойчивой.
8. Н
ахождение области допустимых значений параметра системы АРВ пропорционального действия – 
Как было установлено в предыдущем пункте, система является неустойчивой при  . Необходимо установить такое значение этого коэффициента, при котором корни характеристического уравнения движения системы располагаются только в левой полуплоскости. Это можно осуществить с помощью . Необходимо установить такое значение этого коэффициента, при котором корни характеристического уравнения движения системы располагаются только в левой полуплоскости. Это можно осуществить с помощью  -разбиения по одному параметру. Для этого характеристическое уравнение необходимо привести к виду -разбиения по одному параметру. Для этого характеристическое уравнение необходимо привести к виду
 , ,
где
 – совокупность членов, не зависящих от – совокупность членов, не зависящих от  ; ;
 – совокупность членов, содержащих – совокупность членов, содержащих  множитель. множитель.
 ; ;
 ; ;
 ; ;
 . .
Граница  - разбиения определится при - разбиения определится при  уравнением уравнением
 , (10) , (10)
откуда
 . .
По этому выражению находится значение параметра  (в общем случае комплексного (в общем случае комплексного  ), при котором уравнение (10) имеет один мнимый корень. Давая ), при котором уравнение (10) имеет один мнимый корень. Давая  значение от значение от  до до  , можно вычислить , можно вычислить  и и  и построить на комплексной плоскости и построить на комплексной плоскости  границу границу  -разбиения (рис. 20). Теперь при изменении параметра -разбиения (рис. 20). Теперь при изменении параметра  от от  до до  в плоскости в плоскости  движемся по границе движемся по границе  - разбиения и штрихуем ее слева. Претендентом на область устойчивости является область, внутрь которой направлена штриховка. Поэтому в этой области будет содержаться наибольшее число левых корней. - разбиения и штрихуем ее слева. Претендентом на область устойчивости является область, внутрь которой направлена штриховка. Поэтому в этой области будет содержаться наибольшее число левых корней.

Рисунок 20. Кривая D
-разбиения по одному параметру 
Чтобы установить, является ли эта область действительно областью устойчивости, зададимся каким-либо значением  , лежащим в этой области. Пусть , лежащим в этой области. Пусть  . Используя критерий Михайлова, проверим систему на устойчивость. . Используя критерий Михайлова, проверим систему на устойчивость.
Для этого пересчитаем коэффициенты, содержащие  : :
 ; ;

Тогда по формуле (9):
 . .
Остальные значения останутся прежними.
По полученным значениям строим годограф (рис.21):
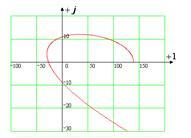
Рисунок 21. Годограф Михайлова для 
Вид годографа удовлетворяет необходимым условиям, поэтому данная область является областью устойчивости.
Так как исследуемый параметр является вещественным числом, то из полученной области выделяется только отрезок устойчивости, представляющий собой отрезок вещественной числовой оси, лежащей в области устойчивости  , (рис. 20). Причем, координаты точек пересечения вещественной оси кривой , (рис. 20). Причем, координаты точек пересечения вещественной оси кривой  -разбиения -разбиения  и и  равны значениям этих же коэффициентов, найденных по выражениям (7) и (8) в соответствии с алгебраическим критерием Гурвица. равны значениям этих же коэффициентов, найденных по выражениям (7) и (8) в соответствии с алгебраическим критерием Гурвица.
Заключительным этапом при выполнении курсовой работы является проверка системы на динамическую устойчивость при больших возмущениях в системе, вызванных коротким замыканием вблизи шин передающей станции и последующим его отключением.
Расчет динамической устойчивости производится при условии сохранения неизменной величины переходной ЭДС  у генераторов станции. Для проверки системы на динамическую устойчивость необходимо на одном графике построить три угловых характеристики передачи, соответствующие нормальному (I), аварийному (II) и послеаварийному (III) режимам работы. Амплитуды указанных характеристик определяются по схемам замещения системы для каждого из указанных режимов работы (рис. 22, 23 и 24). у генераторов станции. Для проверки системы на динамическую устойчивость необходимо на одном графике построить три угловых характеристики передачи, соответствующие нормальному (I), аварийному (II) и послеаварийному (III) режимам работы. Амплитуды указанных характеристик определяются по схемам замещения системы для каждого из указанных режимов работы (рис. 22, 23 и 24).
Сопротивление шунта короткого замыкания, входящее в схему замещения системы в аварийном режиме, определяется сопротивлениями схем замещения обратной и нулевой последовательностей, способ соединения которых между собой

Рисунок 22. Схема замещения системы в нормальном режиме работы

Рисунок 23. Схема замещения системы в аварийном режиме работы
 
Рисунок 24. Схема замещения системы в послеаварийном режиме работы
определяется видом короткого замыкания. Так, для трехфазного короткого замыкания  , двухфазного – , двухфазного –  , однофазного – , однофазного –  и для двухфазного короткого замыкания на землю и для двухфазного короткого замыкания на землю  . .
Величины результирующих сопротивлений обратной и нулевой последовательностей определяются из соответствующих схем замещения системы (рис. 25, 26).

Рисунок 25. Схема замещения системы обратной последовательности
Сопротивление генератора обратной последовательности подсчитывается по формуле
 , ,
где
 – сверхпереходная реактивность генератора и может быть принята для генераторов всех типов равной – сверхпереходная реактивность генератора и может быть принята для генераторов всех типов равной  . .
 . .
После элементарных преобразований схемы (рис. 25) получаем
 ; ;
 . .
При определении результирующего сопротивления нулевой последовательности следует иметь в виду, что трансформатор блока имеет схему соединения обмоток  . Поэтому генератор может быть исключен из схемы замещения нулевой последовательности, а сопротивление трансформатора можно принять равным его сопротивлению прямой последовательности. . Поэтому генератор может быть исключен из схемы замещения нулевой последовательности, а сопротивление трансформатора можно принять равным его сопротивлению прямой последовательности.
Сопротивление нулевой последовательности линии электропередач в значительной степени отличается от сопротивления прямой последовательности и колеблется в весьма широких пределах от  в зависимости от конструктивного исполнения передачи. Для данного курсового проекта приняли в зависимости от конструктивного исполнения передачи. Для данного курсового проекта приняли  . .

Рисунок 26. Схема замещения системы нулевой последовательности
Тогда результирующее сопротивление нулевой последовательности
 ; ;
 , ,
а сопротивление шунта короткого замыкания для двухфазного короткого замыкания на землю подсчитывается по формуле
 ; ;
 . .
Проводимость шунта короткого замыкания:
 ; ;
 . .
Сопротивления связи  , определяющие амплитуды угловых характеристик для каждого из режимов, определяются по схемам замещения системы (рис. 22, 23, 24): , определяющие амплитуды угловых характеристик для каждого из режимов, определяются по схемам замещения системы (рис. 22, 23, 24):
 Тогда амплитуды угловых характеристик, представленных на рис. 27, определяются по формулам: Тогда амплитуды угловых характеристик, представленных на рис. 27, определяются по формулам:
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 . .

Рис. 27. Определение предельного угла отключения аварии
Используя правило площадей (рис. 27), можно найти предельный угол отключения аварии  , величина которого определяется из условия равенства площадки ускорения , величина которого определяется из условия равенства площадки ускорения  площадке торможения площадке торможения  . .
 ; ;
 . .
Величину критического угла можно найти из выражения:
 ; ;
 . .
Тогда
 ; ;

Зная предельный угол отключения аварии, можно определить максимально допустимое время отключения короткого замыкания. Для этого необходимо решить дифференциальное уравнение движения ротора:
 . .
Данное уравнение в силу своей нелинейности может быть решено только численными методами, наиболее предпочтительным из которых является метод последовательных интервалов.
Сущность этого метода заключается в следующем.
Весь процесс качания машины разбивается на ряд небольших и равных между собой интервалов времени. Обычно продолжительность интервала принимается равной  с и для каждого из этих интервалов последовательно вычисляется приближенное значение приращения угла с и для каждого из этих интервалов последовательно вычисляется приближенное значение приращения угла  . .
Возникающий в момент короткого замыкания избыток мощности  сообщает ротору некоторое ускорение сообщает ротору некоторое ускорение  . Для достаточно малого интервала времени . Для достаточно малого интервала времени  можно допустить, что избыток мощности в течение этого периода остается неизменным. Тогда по формулам равноускоренного движения нетрудно вычислить приращение скорости машины можно допустить, что избыток мощности в течение этого периода остается неизменным. Тогда по формулам равноускоренного движения нетрудно вычислить приращение скорости машины  и угла и угла  в течение первого интервала: в течение первого интервала:
 ; ;
 . .
 ; ;

Величина ускорения  и, следовательно, и, следовательно,
 ; ;
здесь угол выражен в градусах, а время – в секундах.
Обозначив
 ; ;
 , ,
получим
 ; ;
 . .
Зная приращение угла в первом интервале, можно найти абсолютное значение угла в конце этого интервала времени:
 ; ;
 . .
Для нового значения угла  можно определить величину избытка мощности можно определить величину избытка мощности  в начале второго интервала времени по формуле в начале второго интервала времени по формуле
 ; ;
 . .
Тогда приращение угла на втором интервале
 ; ;
 . .
Для произвольного  -го интервала приращение угла определяется выражением -го интервала приращение угла определяется выражением
 . .
Получаем, следующие значения (табл.5):
Таблица 5
| 
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
| 
|
25,451
|
26,681
|
30,344
|
36,359
|
44,597
|
54,901
|
67,1
|
| 
|
0
|
0,05
|
0,1
|
0,15
|
0,2
|
0,25
|
0,3
|
Применив совместно метод последовательных интервалов и способ площадей, можно найти максимально допустимое время отключения короткого замыкания. Для этого с помощью метода последовательных интервалов вычисляют время, в течение которого ротор достигает угла  . Этот промежуток времени и соответствует предельному времени отключения короткого замыкания . Этот промежуток времени и соответствует предельному времени отключения короткого замыкания  с (рис. 28). с (рис. 28).

Рисунок 28. Расчет предельного времени отключения аварии
Таким образом, в ходе работы было проведено исследование статической и динамической устойчивости простейшей регулируемой системы, состоящей из генераторной станции, работающей на шины бесконечной мощности через две параллельные линии электропередачи. Анализируя устойчивость системы по алгебраическому критерию Гурвица и частотному критерию Михайлова, выяснили, что система с исходным параметром системы АРВ пропорционального действия –  (см. табл.1) неустойчива. Используя D-разбиение, была найдена область допустимых значений (см. табл.1) неустойчива. Используя D-разбиение, была найдена область допустимых значений  . Кроме того, произведен расчет динамической устойчивости системы с определением предельного угла отключения аварии при двухполюсном коротком замыкании на землю одной из параллельных линий вблизи шин генераторной станции. . Кроме того, произведен расчет динамической устойчивости системы с определением предельного угла отключения аварии при двухполюсном коротком замыкании на землю одной из параллельных линий вблизи шин генераторной станции.
1. Столбов Ю.А., Пястолов В.В. Электромеханические переходные процессы: Учебное пособие по курсовому проектированию.– Челябинск: ЮУрГУ, 2005. – 47 с.;
2. Веников В.А. Переходные электромеханические процессы в электрических системах.- Москва: ВШ, 1978. – 415 с.;
3. СТП.– Челябинск: ЮУрГУ, 2001.
|
![]() . Этот промежуток времени и соответствует предельному времени отключения короткого замыкания
. Этот промежуток времени и соответствует предельному времени отключения короткого замыкания ![]() с (рис. 28).
с (рис. 28).
![]() (см. табл.1) неустойчива. Используя D-разбиение, была найдена область допустимых значений
(см. табл.1) неустойчива. Используя D-разбиение, была найдена область допустимых значений ![]() . Кроме того, произведен расчет динамической устойчивости системы с определением предельного угла отключения аварии при двухполюсном коротком замыкании на землю одной из параллельных линий вблизи шин генераторной станции.
. Кроме того, произведен расчет динамической устойчивости системы с определением предельного угла отключения аварии при двухполюсном коротком замыкании на землю одной из параллельных линий вблизи шин генераторной станции.

 – действительный радиус провода, мм:
– действительный радиус провода, мм: ;
;






 ,
,
 ,
,











 , с
, с .
.

 ,
, .
. и второй
и второй  . Их геометрическая сумма и дает комплекс мощности
. Их геометрическая сумма и дает комплекс мощности  и
и  .
. остаются неизменными по величине и по фазе, а комплексы
остаются неизменными по величине и по фазе, а комплексы  и
и  , оставаясь неизменными по величине, изменяют угол поворота с изменением угла
, оставаясь неизменными по величине, изменяют угол поворота с изменением угла 
 , где
, где 













 .
. .
.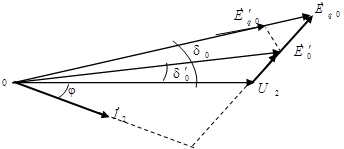






 ; причем для отстающего тока в индуктивном квадранте берется знак «-», а для опережающего тока, соответствующего емкостному квадранту, – знак «+
».
; причем для отстающего тока в индуктивном квадранте берется знак «-», а для опережающего тока, соответствующего емкостному квадранту, – знак «+
». .
.
 ,
, – синхронизирующая мощность в окрестности угла
– синхронизирующая мощность в окрестности угла 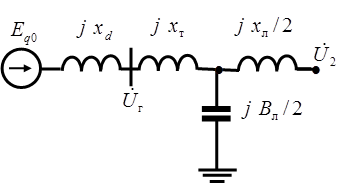


 .
. ,
, .
. .
.

 .
. .
. ,
, .
. .
. ,
, – декремент затухания амплитуды колебаний:
– декремент затухания амплитуды колебаний:
 – частота колебаний.
– частота колебаний. , где
, где  ,
,



 (1)
(1)

 . (2)
. (2)
 или с учетом того, что
или с учетом того, что  . (3)
. (3)  .
. ,
,  .
. .
.
 .
. , а
, а  ,
, , (5)
, (5) . (6)
. (6)
 – передаточная функция колебательного звена;
– передаточная функция колебательного звена; .
. и принужденной составляющей
и принужденной составляющей  .
. и
и  .
. .
.
 ,
, .
. .
. ,
, ,
, .
.
 .
. .
.
 ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
;  ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; ,
, ;
; .
. и
и  , содержащие коэффициент усиления системы, в большой степени влияют на величину коэффициентов характеристического уравнения и, тем самым, на устойчивость системы.
, содержащие коэффициент усиления системы, в большой степени влияют на величину коэффициентов характеристического уравнения и, тем самым, на устойчивость системы. ;
; ;
; .
. .
. . (7)
. (7)
 (8)
(8) .
.
 , то система устойчива. Если же этот угол отличается от
, то система устойчива. Если же этот угол отличается от  , то система неустойчива. При этом за положительный угол поворота считается направление против часовой стрелки. Для уравнения четвертой степени в устойчивой системе конец вектора
, то система неустойчива. При этом за положительный угол поворота считается направление против часовой стрелки. Для уравнения четвертой степени в устойчивой системе конец вектора  и описать годограф. Таким образом, для найденного
и описать годограф. Таким образом, для найденного 
 ;
; .
. .
.
 ;
;




 .
.
 ,
, .
. ;
; .
.
 ;
; ,
, ;
; .
. ;
; .
. Тогда амплитуды угловых характеристик, представленных на рис. 27, определяются по формулам:
Тогда амплитуды угловых характеристик, представленных на рис. 27, определяются по формулам: ;
; ;
; ;
; ;
; ;
; .
.
 ;
; .
. ;
; .
. ;
;
 .
. и, следовательно,
и, следовательно, ;
; ;
; ,
, ;
; .
.