СОДЕРЖАНИЕ
Введение
1. Механика твёрдого тела. Динамика поступательного и вращательного движения твёрдого тела. Определение момента инерции тела с помощью маятника Обербека
Контрольные вопросы
Решение
2. Колебания и волны
2.1 Кинематика колебательного движения
Контрольные вопросы
Решение
2.2Динамика колебательного движения
Контрольные вопросы
Решение
Заключение
Список литературы
Целью расчётно-графической работы является углубление и закрепление знания основных понятий и законов двух разделов: «Механика твёрдого тела» и «Гармонические колебания». Для того, чтобы укрепить знания по разделу «Механика твёрдого тела» необходимо с помощью маятника Обербека исследовать зависимость углового ускорения от момента внешней силы при условии, что I
0
=
const
, и зависимость момента инерции от расстояния грузов до оси вращения, рассчитав при этом момент инерции согласно теореме Штейнера.
1. МЕХАНИКА ТВЁРДОГО ТЕЛА ДИНАМИКА ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
Контрольные вопросы
1. Момент инерции точки
относительно данной оси – скалярная величина, равная произведению массы точки на квадрат расстояния от этой точки до оси. (Ii
=
mi
ri
2
). Момент инерции тела
относительно оси вращения – физическая велиина равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси. (I=ΣIi
=Σmi
ri
)
2. Роль момента инерции во вращательном движении.
Момент инерции является мерой инертности тела при вращательном движении подобно тому, как масса есть мера инертности при поступательном движении. Момент инертности показывает распределение массы в пространстве относительно оси вращения.
3. Рассмотрим сечение твердого тела произвольной формы, изображенное на рисунке

Выберем координатную систему XY
с началом координат O
в центре масс C
тела. Пусть одна из осей вращения проходит через центр масс C
, а другая через произвольную точку P
, расположенную на расстоянии d
от начала координат. Обе оси перпендикулярны плоскости чертежа. Пусть Δm
i
– некоторый малый элемент массы твердого тела. По определению момента инерции:
 
Выражение для IP
можно переписать в виде:

Поскольку начало координат совпадает с центром масс C, последние два члена обращаются в нуль. Это следует из определения центра масс. Следовательно, I
0
=
Ic
+
ma
2
=0,5
mR
2
+
m
=1,5
mR
2
где m – полная масса тела.
Теорема Штейнера:
момент инерции тела относительно любой оси вращения равен моменту его инерции
Ic
относительно оси, проходящей через центр масс плюс произведение массы тела на квадрат расстояния «а» между осями.
4. Момент силы относительно неподвижной оси
– скалярная величина М равная проекции на эту ось вектора момента силы  , определённого относительно произвольной точки на данной оси Z. Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки
равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы: , определённого относительно произвольной точки на данной оси Z. Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки
равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы: Направление момента силы совпадает с направлением поступательного движения правого винта при его вращении. Направление момента силы совпадает с направлением поступательного движения правого винта при его вращении.
Уравнение динамики вращательного движения тела
: Элементарная работа всех внешних сил при таком повороте равна элементарному изменению кинетичекой энергии:
dA=dEk
=> M=dε => M=Idω/dt
=> M=d(Iω)/dt
5. M
=
Iε
– это основное уравнение динамики вращательного движения тела
: угловое ускорение вращающегося тела прямо пропорционально сумме моментов всех действующих на него сил относительно оси вращения тела и обратно пропорционально моменту инерции тела относительно этой оси вращения. Полученное уравнение аналогично по форме записи выражению второго закона Ньютона для поступательного движения тела:F
=
ma
Ускорению поступательного движения тела а
соответствует угловое ускорение вращательного движения ε
. Аналогом силыF
при поступательном движении, является момент силы М
во вращательном движении, а аналогом массы тела m
при поступательном движении, служит момент инерции тела I
при вращательном движении.
Решение
| Вариант |
m0 |
m |
m1 |
m2 |
m3 |
l1 |
l2 |
l3 |
a |
R |
| 22 |
0,04
|
0,2
|
0,2
|
0,1
|
0,3
|
0,3
|
0,1
|
0,5
|
0,3
|
0,03
|
Найдём момент инерции
J
0
системы, если известны масса груза
m
, радиус блока
R
,
l
=0, трением пренебречь.
J0
=m(g-a)R/ε=m(g-a)R2
/a
Вычислим и получим результат:J
0
=0,0057кгм2
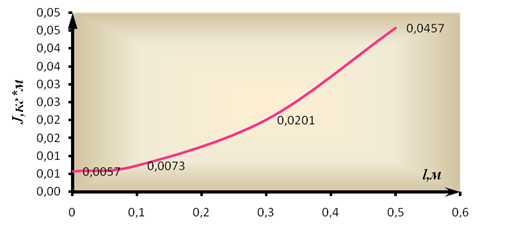
Строим график зависимости
J
=
f
(
l
)
при
l
1
,
l
2
,
l
3
.
Момент инерции маятника Обербека согласно теореме Штейнера может быть записан в виде:
J
=
J
0
+4
m
0
l
2
где l
– расстояние центров грузов m
от оси вращения.
Рассчитаем момент инерции системы для различных l
:
при l
=0 J
=
J
0
=
0,0057кгм2
при l
1
=0,3 J
1
=0,0201кгм2
при l
2
=0,1 J
2
=
0,0073кгм2
при l
3
=0,5 J
3
=
0,0457кгм2
Составим таблицу результатов расчётов и отразим это графиком:
| l, м |
0 |
0,3 |
0,1 |
0,5 |
| J, кгм2
|
0,0057 |
0,0201 |
0,0073 |
0,0457 |
2. Строим график зависимости ε=
f
(
M
)
при
m
1
,
m
2
,
m
3
при
J
=
const
Вращающий момент равен M
=
TR
, где силу натяжения нити T
находим из уравнения T
=
m
(
g
-
a
),
тогда M
=
m
(
g
-
a
)
R
.
Из основного уравнения динамики для вращательного движения находим главное угловое ускорение:ε=
m
/
J
=
m
(
g
-
a
)
R
/
J
, где J
=const(по условию)
Возьмём значение момента инерции из п.2: J
=
J
0
=
0,0057 кгм2
Сделаем расчёт вращающего момена М
при различных значениях m:
при m
1
=0,2 M
1
=
0,2(9,8-0,3)0,03=0,057Нм
при m
2
=0,1 M
2
=
0,1(9,8-0,3)0,03=0,0285Нм
при m
3
=0,3 M
3
=
0,3(9,8-0,3)0,03=0,0855Нм
Сделаем расчёт для углового ускорения ε
:
при m
1
=0,2 ε=
M
1
/
J
0
=
10с-2
при m
2
=0,1 ε=
M
2
/
J
0
=
5с-2
при m
3
=0,3 ε=
M
3
/
J
0
=
15с-2
Составим таблицу результатов расчёта и отразим это графиком:
| m, кг |
0,1 |
0,2 |
0,3 |
| M, Н*м |
0,0285 |
0,057 |
0,0855 |
| ε, с-2 |
5 |
10 |
15 |
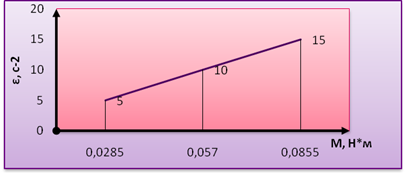
Мы получили линейную зависимость ε
от М
при J
=
const
и различных массах m
1
, m
2
, m
3
.
2. Колебания и волны
2.1 Кинематика колебательного движения
Контрольные вопросы
1. Колебания
– это процессы обладающие некоторой повторяемостью во времени. Гармонические колебания – колебания, происходящие по закону синуса и косинуса. Амплитуда – максимальное отклонение колеблющейся величины от положения равновесия в данный момент времени. Фаза – угловое отклонение колеблющейся величины от положения равновесия в данный момент времени. Циклическая частота – число колебаний за 2π единиц времени. Период – время одного полного колебания.
2. Дано: А=5см; Т=4с; φ0
=π/2 Уравнение: ω=2π/T=π/2 => х=5sin(π/2t+π/2)
при t1
=0, Х=0; при t2
=1,5, Х=-5.

3. Дано: А=5 см; Т=8, ω = π/4(по формуле п.2). Написать уравнение гармонического колебания:
a. φ0
=0; x=5cos(π/4t+0)= 5cos(π/4t)
b. φ0
=π/2; x=5cos(π/4t+ π/2)=-5cos(π/4t)
c. φ0
=π; x=5cos(π/4t+π)=-5cos(π/4t)
d. φ0
=3π/2; x=5cos(π/4t+3π/2)=5sin(π/4t)
e. φ0
=2π; x=5cos(π/4t+2π)= 5cos(π/4t)
| X=Acos(ωt+φ0) |
t=5c |
| A=5м |
ω=π |
φ0=π |
Из уравнения гармонического колебательного движения точки определяем смещение точки и строим график
X
=
f
(
t
) в пределах одного периода:
X
=
Acos
(
ωt
+
φ
0
)= 5
cos
(
πt
+
π
приt
1
=
4 c; X
1
=
-5
приt
2
=
4,5с; X
2
=
0
приt
3
= 5с;X
3
=
5
приt
4
= 5,5с;X
4
=
0
приt
5
= 6с; X
5
=
-5Период равен:T
=2π/ω=2
c
2.
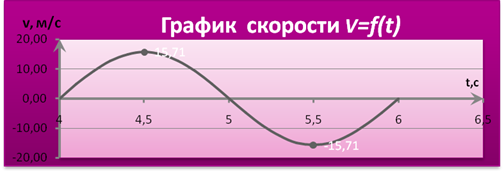
Определяем скорость колеблющейся точки и по результатам расчёта строим график
 в пределах одного периода: в пределах одного периода:

При t
1
=4 cV
1
= 0
Приt
2
=4,5 cV
2
=
15,7 м/с
При t
3
=5 cV
3
= 0
При t
4
=5,5 cV
4
=-15,7 м/с
При t
5
=6 cV
5
= 0
| t,с |
4 |
4,5 |
5 |
5,5 |
6 |
| V,м/с |
0 |
15,7 |
0 |
-15,7 |
0 |
3.
Определяем ускорение колеблющейся точки и по результатам расчёта строим
a
=
f
(
t
)
график.
A=dv/dt=-Aω2
cos(ωt+φ0
)=-5π2
cos(πt+π/2)
Приt1
=4 c, a1
= 0
Приt
2
=4,5c,a
2
=
49,3 м/с2
При t
3
=5 c,a
3
=
0
При t
4
=5,5 c,a
4
=
-49,3 м/с2
При t
5
=6 c,a
5
=
0
| t,c |
4 |
4,5 |
5 |
5,5 |
6 |
| X, м |
-5 |
0 |
5 |
0 |
-5 |
| t, c |
4 |
4,5 |
5 |
5,5 |
6 |
| a, м/с2 |
0 |
49,3 |
0 |
-49,3 |
0 |
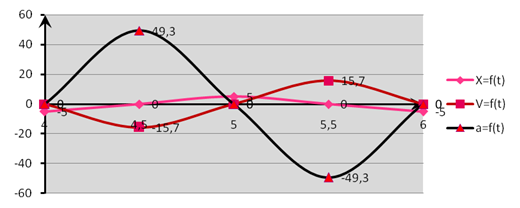
4. Для большей наглядности сведём все три графика X=f(t), V=f(t), a=f(t) на одни оси.
· Сила действующая на колеблющуюся материальную. точку массой m:
· F= - mω0
x
· Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания: Ek
=
mA
2
ω2
cos
2
(ω
t
+φ)/2
· Потенциальная энергия материальной точки, совершающей гармонические колебания:E
п
=
E
0
sin
2
(ω
t
+φ)
· Полная энергия материальной точки, совершающей гармонические колебания: E
=
mA
2
ω2
/2
1. Дано: x=0,1sin(π/8•t+π/4), m=0,16 кг.
Fmax
=F0
=mAω2
=0,16*0,1*(π/8)2
=0,003H
F=-F0
sin(ωt+φ)=-0,52sin(π/8•t+π/4)

При t
1
=0c, F
1
=-0,37
H
Приt
2
=1c, F
2
=
-0,48
H
При t
3
=2 c, F
3
=
-0,52
H
При t
4
=3 c, F
4
=
-0,48
H
При t
5
=4с, F
5
=-0,37H
При t
6
=5c, F
6
=
-0,2
H
При t
7
=6,F
7
=0H
При t
8
=7, F
8
=
0,2H
При t
9
=8,F
9
=
0,37
2. Дано: m=0,16 кг, x=2sin(π/4·t+π/4)
E0
=E
пол
=
0,16·4(π/4)2
/2=0,2Дж
Ek
=E0
cos2
(ωt+φ)=0,2cos2
(π/4·t+π/4)
Eп
=E0
sin2
(ωt+φ) =0,2sin2
(π/4·t+π/4)
При t
1
=0 c,Ek
1
=0,1Дж E
п
=0,1Дж
Приt
2
=0,5 c,Ek
2
=0,03ДжE
п
=0,17Дж
При t
3
=1 c,Ek
3
=0E
п
=0,2Дж
При t
4
=1,5 c,Ek
4
=0,03ДжE
п
=0,17Дж
При t
5
=2 c, Ek
5
= 0,1ДжE
п
=0,1Дж

| Вариант |
X=f(t) |
m, кг |
t, c |
A, м |
ω, с-1 |
φ0, рад |
| 22 |
Asin(ωt+φ0) |
0,12 |
3 |
7 |
π/4 |
π/2 |
1. Найдём силу для момента времени t
и максимальную силу Fm
:
F= - mA(π/4)2
sin(π/4·t+π/2)=0,37H
Fmax
=F0
=mAω2
=0,52H
F=-F0
sin(ωt+φ)= - 0,52 sin(π/4·t+π/2)
При t
1
=1 c, F
1
=-
0,37H
Приt
2
=1,5c, F
2
= -
0,2H
При t
3
=2 c, F
3
=
0
При t
4
=2,5 c, F
4
=
0,2H
При t
5
=3c, F
5
=
0,37H
При t
6
=3,5,F
6
=0,48H
При t
7
=4, F
7
=
0,52H
При t
8
=4,5,F
8
=
0,48H
При t
9
=5, F
9
=
0,37H
При t
10
= 5,5c, F
10
=0,2H
Приt
11
=6c, F
11
=
0
При t
12
=6,5 c, F
12
= -
0,2H
При t
13
=7 c, F
13
= -
0,37H
| t, c |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
| F, H |
-0,37 |
-0,2 |
0 |
0,2 |
0,37 |
0,48 |
0,52 |
0,48 |
0,37 |
0,2 |
0 |
-0,2 |
-0,37 |

2.
Найдём максимальную кинетическую энергию:
E0
=Ekmax
=mA2
ω2
/2=1,81
Дж
3.
Найдём кинетическую и потенциальную энергию для момента времени
t
=3
c
:
Ek
=
mV
2
/2=
mA
2
ω
2
cos
2
(ω
t
+φ)/2=0,86Дж
E
п(
max
)
=
E
0
=1,81Дж
Ek
=
E
0
cos
2
(ω
t
+φ)=
E
0
cos
2
(
π
/4·
t
+
π
/2)
При t
1
=0 c,Ek
1
=0 Дж
Приt
2
=0,5c, Ek
2
=0,27Дж
При t
3
=1 c,Ek
3
=0,9Дж
При t
4
=1,5 c,Ek
4
=1,53Дж
При t
5
=2 c,Ek
5
= 1,81Дж
При t
6
=2,5Ek
6
=1,53Дж
При t
7
=3Ek
7
=0,9Дж
При t
8
=3,5Ek
8
=0,27Дж
При t
9
=4, Ek
9
=0
При t
10
=4,5Ek
10
=0,27Дж
При t
11
=5Ek
11
=0,9Дж
При t
12
=5,5Ek
12
=1,53Дж
При t
13
=6Ek
13
= 1,81Дж
Приt
14
=6,5Ek
14
=1,53Дж
При t
15
=7Ek
15
=0,9Дж
Приt
16
=7,5 Ek
16
=0,27Дж
Приt
17
=8, Ek
17
=0
Т.к E0
=1,81 Дж (из п.2)
| t,с |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
| F,Н |
0 |
0,27 |
0,9 |
1,53 |
1,81 |
1,53 |
0,9 |
0,27 |
0 |
0,27 |
0,9 |
1,53 |
1,81 |
1,53 |
0,9 |
0,27 |
0 |

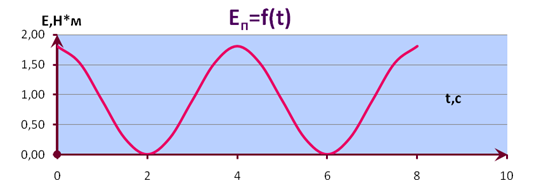
Найдём значение потенциальной энергии для отдельных моментов времени в пределах одного периода:
E
п
=Епол
-Ек
=
mA
2
ω
2
/2 –
mA
2
ω
2
cos
2
(ω
t
+φ)/2=
E
0
sin
2
(π/4·
t
+π/2)
При t
1
=0 c,E
п1
=1,81Дж
Приt
2
=0,5 c,E
п2
=1,53Дж
При t
3
=1 c,E
п3
=0,9Дж
При t
4
=1,5 c,E
п4
=0,27Дж
При t
5
=2 c,E
п5
= 0
При t
6
=2,5E
п6
=0,27Дж
При t
7
=3E
п7
=0,9Дж
При t
8
=3,5E
п8
=1,53Дж
При t
9
=4, E
п9
=1,81Дж
При t
10
=4,5E
п10
=1,53Дж
При t
11
=5E
п11
=0,9Дж
При t
12
=5,5E
п12
=0,27Дж
При t
13
=6E
п13
= 0
Приt
14
=6,5E
п14
=0,27Дж
При t
15
=7E
п15
=0,9Дж
Приt
16
=7,5E
п16
=1,53Дж
Приt
17
=8, E
п17
=1,81Дж
Заключение
В этой расчётно-графической работе мы исследовали зависимости при определении момента инерции тела с помощью маятника Обербека, а также на примере проследили действие законов из таких разделов физики, как «Механика твёрдого тела» и «Колебания и волны». Данная расчётно-графическая работа актуальна, так как она помогает овладеть аналитико-синтетическим методом, усилив внимание на качественной стороне физической сущности явлений; развивает практические навыки работы со справочной литературой; помогает овладеть элементами научно-исследовательской и самостоятельной творческой работы; позволяет использовать один из вариантов внедрения ПК в учебный процесс с помощью решения задач и построения графиков.
Список литературы
1. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1999 г.
2. Бачище А.В. Краткий курс общей физики. Механика. Молекулярная физика. Термодинамика. – Новороссийск: НГМА, 1999 г.
|