Задание 1
Вычислите 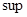 и и 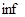 последовательности последовательности  . .
Решение.
Рассмотрим последовательность 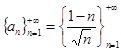 . .
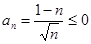 для любого натурального для любого натурального 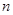
Следовательно, множество 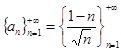 является ограниченным сверху. Это означает, что последовательность является ограниченным сверху. Это означает, что последовательность 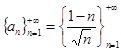 имеет верхнюю точную грань: имеет верхнюю точную грань: 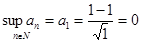 . .
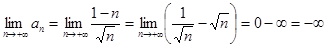
Следовательно, множество 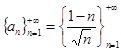 не является ограниченным снизу. Это означает, что нижняя грань не является ограниченным снизу. Это означает, что нижняя грань 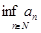 последовательности последовательности 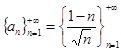 не существует. не существует.
Ответ.
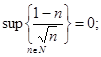 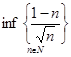 не существует не существует
Задание 2
Пользуясь определением предела последовательности, докажите, что 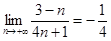 . .
Доказательство.
Число 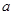 называется пределом последовательности называется пределом последовательности 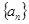 , если для любого положительного числа , если для любого положительного числа 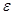 существует номер существует номер 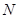 такой, что при такой, что при  выполняется неравенство выполняется неравенство 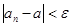 . .
Используя определение предела последовательности, докажем, что 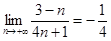 . .
Возьмем любое число 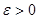 . .
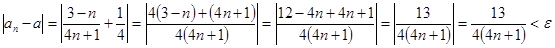
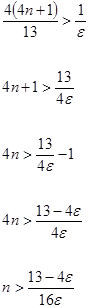
Если взять  , то для всех , то для всех  будет выполняться неравенство будет выполняться неравенство 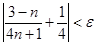 . Следовательно, . Следовательно, 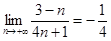 . .
Доказано
Задание 3
Пользуясь определением предела функции, докажите, что 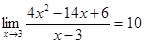 . .
Доказательство
Число 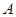 называется пределом функции называется пределом функции 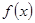 при при 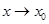 , если для любого числа , если для любого числа 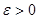 существует число существует число 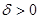 такое, что для всех такое, что для всех 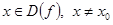 , удовлетворяющих неравенству , удовлетворяющих неравенству 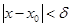 , выполняется неравенство , выполняется неравенство 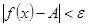 . .
Используя определение предела функции, докажем, что 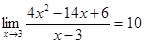 . .
Возьмем любое 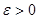 . .
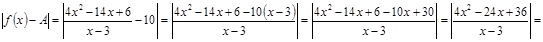
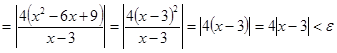

Положим 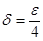 . .
Если взять 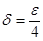 , то для всех , то для всех 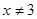 , удовлетворяющих неравенству , удовлетворяющих неравенству 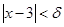 , выполняется неравенство , выполняется неравенство 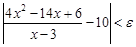 . Следовательно, . Следовательно, 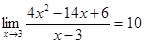 . .
Доказано.
Задание 4
Вычислите предел 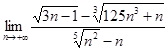 . .
Решение.


Ответ.
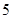
Задание 5
Вычислите предел  . .
Решение.
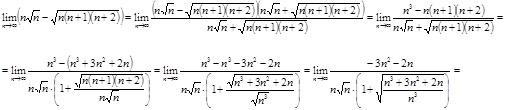
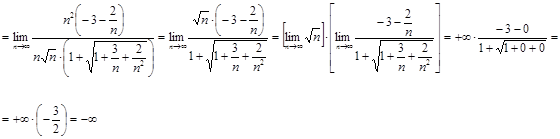
Ответ.
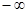
Задание 6
Вычислить предел 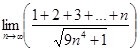 . .
Решение.
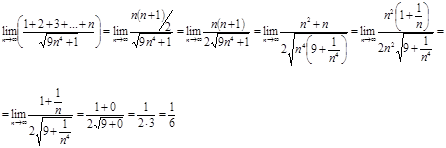
Ответ.
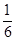
Задание 7
Вычислить предел 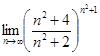 . .
Решение.
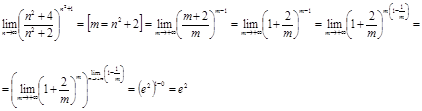
Ответ.
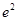
Задание 8
Вычислить предел 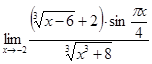 . .
Решение
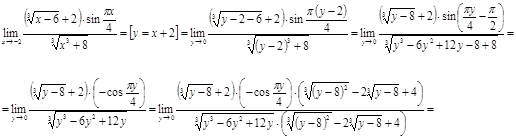
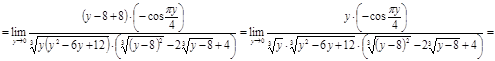
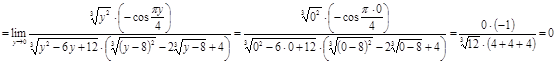
Ответ.

Задание 9
Вычислить предел 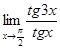 . .
Решение.
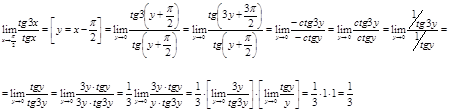
Ответ.
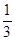
Задание 10
Вычислить предел 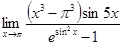 . .
Решение.
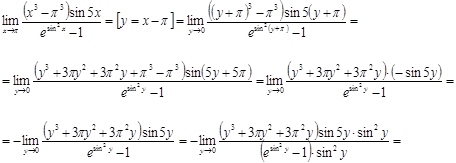
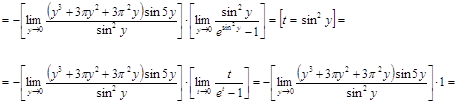
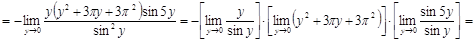
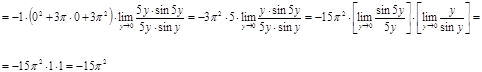
Ответ.
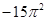
Задание 11
Вычислить предел 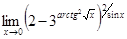 . .
Решение.
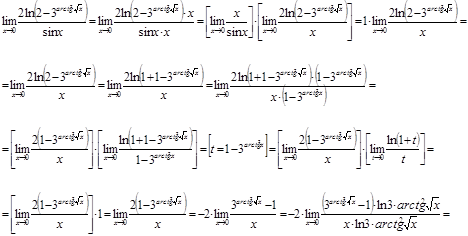
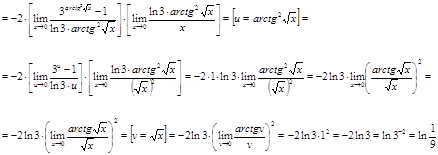
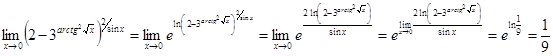
Ответ.
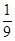
Задание 12
Вычислить предел  . .
Решение.
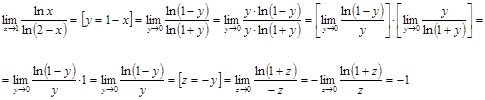

Ответ.
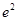
Задание 13
Вычислить предел 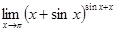 . .
Решение.

Ответ.
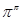
Задание 14
Вычислить предел 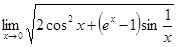 . .
Решение.
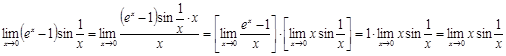
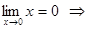 при при 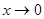 функция функция 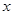 является бесконечно малой является бесконечно малой
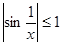 для любого для любого 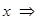 функция функция  является ограниченной. является ограниченной.
Известно, что произведение бесконечно малой функции и ограниченной функции есть бесконечно малая функция. Следовательно, функция 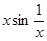 является бесконечно малой при является бесконечно малой при 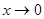 . Это означает, что . Это означает, что 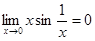 . .
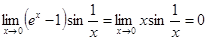
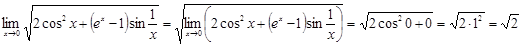
Ответ. 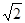
|