МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
КУРСОВАЯ РАБОТА
по дисциплине
Теоретические основы электротехники
Тема
Расчет сложных электрических цепей гармонического тока
МОСКВА 2009 г.
1. Введение
1.1 Цель работы
1. Освоить применение метода комплексных амплитуд к расчёту сложных цепей гармонического тока;
2. Приобрести навыки расчёта комплексных величин и проверки баланса мощностей;
3. Научиться проводить построение векторных диаграмм токов и напряжений для цепей гармонического тока.
1.2 Решаемая задача
Для заданной цепи рассчитать методом контурных токов мгновенное значение токов в ветвях, проверить баланс мощностей, проверить векторную диаграмму токов и напряжений.
Для этого выполняем следующее:
а) выписываем индивидуальные исходные данные для выполнения контрольного домашнего задания;
б) изображаем граф и схему цепи и обозначаем её элементы;
в) подготавливаем схему цепи для расчёта методом контурных токов, для чего преобразовываем генераторы тока в эквивалентные генераторы напряжения;
г) произвольно выбираем положительное направление токов в ветвях и контурных токов;
д) составляем систему уравнений цепи относительно комплексных амплитуд контурных токов;
е) составляем таблицу числовых коэффициентов системы уравнений;
ж) производим расчёт комплексных амплитуд контурных токов;
з) определяем комплексные амплитуды и записываем мгновенные значения токов в ветвях;
и) проверяем баланс мощностей;
к) строим векторные диаграммы токов и напряжений для заданных узла и контура;
л) делаем выводы по результатам выполненного контрольного домашнего задания.
1.3 Исходные данные.
Задание №9, вариант схемы №1.
| Элементы участков цепи |
№ контура для векторной диаграммы напряжений |
Узел для векторной диаграммы токов |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
, Ом
|
, Ом
|
, Ом
|
, Ом
|
, Ом
|
, Ом
|
, Ом
|
, Ом
|
, Ом
|
, Ом
|
, В
|
, Ом
|
, В
|
, Ом
|
, А
|
,
С
м
|
| J12 |
-j8 |
6 |
5-j11 |
10-j4 |
16 |
8-j2 |
J3 |
5+j8 |
4-j10 |
10sin(ωt +110є) |
-j5 |
5sin(ωt+38є) |
10 |
1,2sin(ωt+63є) |
-j0,04 |
II |
В |
2. Расчет цепи методом контурных токов
2.1 Подготовка схемы
При расчёте цепи используем метод контурных токов. Выбор этого метода объясняется тем, что количество независимых контуров в схеме меньше числа ветвей, что определяет количество уравнений, составляемых по второму закону Кирхгофа.
По данному графу изображаем принципиальную схему цепи, для чего, в соответствующие участки графа включаем заданные элементы.
Подготавливаем схему цепи для расчёта методом контурных токов, для чего преобразовываем генератор тока в эквивалентный генератор напряжения и далее рассматриваем цепь только с источниками э.д.с.
Пересчёт параметров генератора тока в эквивалентный генератор напряжения производим по формулам:
 ,   .
 
2.2 Выбор токов в ветвях и контурных токов
Изображаем принципиальную схему цепи после проведения преобразований источников энергии.
Выбираем положительные направления токов в ветвях и контурных токов.
2.3 Система уравнений цепи относительно комплексных амплитуд контурных токов
Составляем  уравнения по второму закону Кирхгофа:
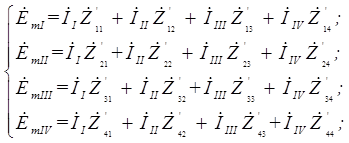
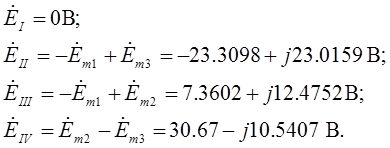
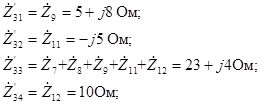
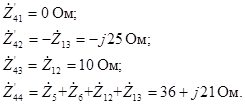
2.4 Таблица числовых коэффициентов системы уравнений
| Коэффициенты системы уравнений |
Левые части уравнений |
| K=1 |
K=2 |
K=3 |
K=4 |
K=5 |
| Re |
Im |
Re |
Im |
Re |
Im |
Re |
Im |
Re |
Im |
| А(1, К) |
9 |
2 |
-4 |
10 |
5 |
8 |
0 |
0 |
0 |
0 |
| А(2, К) |
-4 |
10 |
15 |
-1 |
0 |
-5 |
0 |
-25 |
-23.3098 |
23.0159 |
| А(3, К) |
5 |
8 |
0 |
-5 |
23 |
4 |
10 |
0 |
7.3602 |
12.4752 |
| А(4, К) |
0 |
0 |
0 |
-25 |
10 |
0 |
36 |
21 |
30.67 |
10.5407 |
2.5 Расчёт комплексных амплитуд контурных токов
Для расчета комплексных амплитуд контурных токов находим определители матриц и вычисляем искомые токи по методу Крамера:
 
 
После выполнения расчета проверим правильность полученного результата. Для этого найденные комплексные амплитуды контурных токов подставим в одно из уравнений системы, например, в третье:
( )(5+j8)+( )( - j5)+( )(23+j4)+
+( )(10)= 7.3593+j12.475 В;
7.3593+j12.475 В = 7.3602+j12.4752 В.
В результате проверки выяснилось, что появилась небольшая погрешность. Это говорит о том, что метод контурных токов дает практически точный результат.
2.6 Определение комплексных амплитуд и мгновенных значений токов в ветвях
Комплексная амплитуда тока в ветви определяется как алгебраическая сумма комплексных амплитуд контурных токов, протекающих в данной ветви. Если направление контурного тока совпадает с выбранным ранее направлением тока в ветви, то комплексная амплитуда контурного тока берется со знаком «+», если противоположно – со знаком «–».
  
После определения комплексных амплитуд токов в ветвях запишем их мгновенные значения по формуле:
 ,
где
   
 
 
2.7 Уравнение баланса мощностей
Для того, чтобы убедиться в правильности расчета токов, составляем уравнение баланса мощностей для заданной цепи гармонического тока:
 .
Левая часть уравнения описывает полную мощность источников энергии, которая определяется как алгебраическая сумма мощностей, отдаваемых каждым источником. Со знаком «+» берется слагаемое при совпадении направлений э.д.с. и протекающего в этой ветви тока, в противном случае слагаемое берется со знаком «–».
Правая часть уравнения характеризует полную мощность, потребляемую всеми пассивными элементами цепи.
Комплексное уравнение баланса мощностей при расчетах распадается на два вещественных:  и  , где  - активные мощности;  - реактивные мощности.
Точность расчета токов должна обеспечить выполнение равенств с ошибкой не более 5%:
2.8 Векторная диаграмма комплексных амплитуд токов для заданного узла
Составляем уравнение баланса токов для узла В и строим векторную диаграмму комплексных амплитуд токов согласно первому закону Кирхгофа:
0 = 0.
Аргументы токов узла В:
Модули токов узла В:
 Im
0.5
   Re
0 0.5 1
 Im10
-0.5
 Im9
Im11
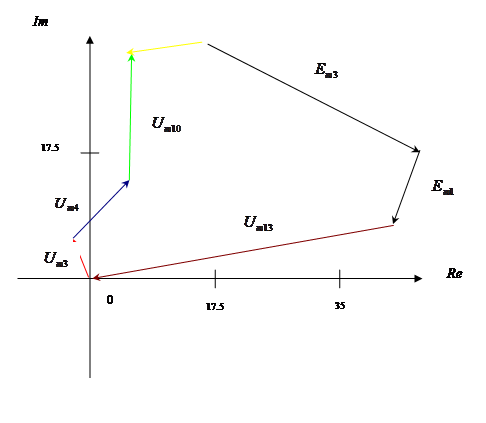
2.9 Векторная диаграмма напряжений для заданного контура
Для построения векторной диаграммы напряжений рассчитаем комплексные амплитуды напряжений на всех элементах заданного контура. Затем, выбрав положительное направление обхода контура, составим уравнение по второму закону Кирхгофа: алгебраическая сумма падений напряжений на элементах замкнутого контура равна алгебраической сумме э.д.с., действующих в этом контуре. Для II-го контура имеем:
 -23.31+j23.016 = -23.31+j23.016.
Рассчитаем комплексные амплитуды напряжений на всех элементах контура:
  
Аргументы напряжений контура:
Модули напряжений контура:
 Выводы
Метод контурных токов удобно применять для расчёта сложных цепей гармонического тока, он позволяет определить токи в ветвях и определить баланс токов, напряжений и мощностей с большой степенью точности.
Литература
1.В.А. Сергеев «Теоретические основы электротехники» Москва 1985 год
2. В.В. Сурков «Статистический анализ расчета цепей постоянного тока» Москва 1971 год
|
