1. (237)
Эта вероятность равна 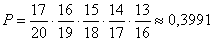
Первая дробь 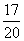 показывает вероятность того, что первому студенту достался билет со сложными вопросами (их 17 из 20)
показывает вероятность того, что первому студенту достался билет со сложными вопросами (их 17 из 20)
Вторая дробь 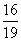 показывает вероятность того, что второму студенту достался билет со сложными вопросами (их осталось 16 из 19)
показывает вероятность того, что второму студенту достался билет со сложными вопросами (их осталось 16 из 19)
Третья дробь 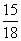 показывает вероятность того, что третьему студенту достался билет со сложными вопросами (их осталось 15 из 18)
показывает вероятность того, что третьему студенту достался билет со сложными вопросами (их осталось 15 из 18)
И так далее до пятого студента. Вероятности перемножаются т.к. по условию требуется одновременное выполнение этих условий.
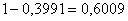
2. (248) Задана функция распределения
F(
x) непрерывной случайной величины Х. Требуется:
1)
f(
x)
2)
3)
F(
x) и
f(
x)
4)
5)
a ,
b)

Решение:
1. Используем свойство 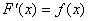 . Получаем:
. Получаем:
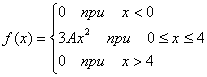
2. Используем свойство 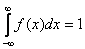
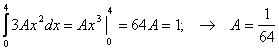
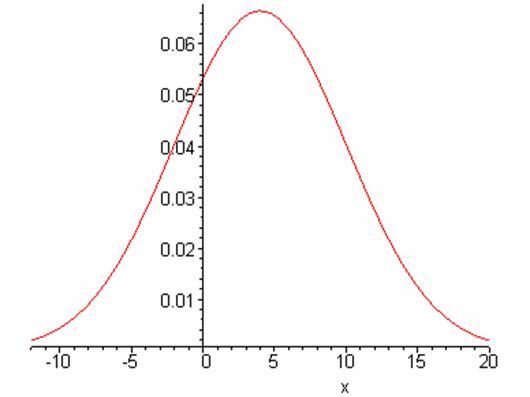
3. Ниже показаны графики функции распределения и плотности распределения.
f(x)
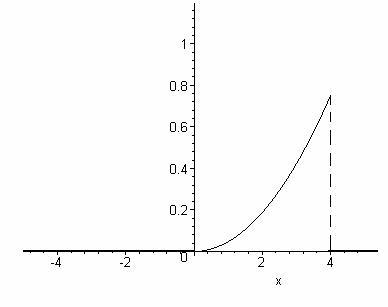
F(x)

4. Математическое ожидание:
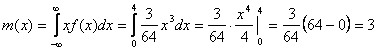
Дисперсия: 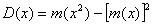
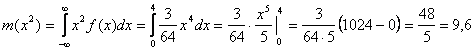
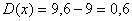
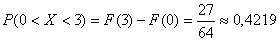
3. (258) Заданы математическое ожидание а = 4
s = 6 нормально распределенной случайной величины. Требуется
Для решения необходимо знать, что нормальным называют распределение вероятностей непрерывной случайной величины, если дифференциальная функция имеет вид:
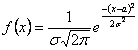
где а – мат. ожидание;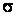 - среднее квадратичное отклонение
- среднее квадратичное отклонение
Вероятность того, что Х примет значение, принадлежащее интервалу 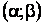 равна:
равна:
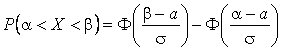
где  - функция Лапласа.
- функция Лапласа.
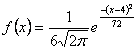
Вероятность того, что Х примет значение, принадлежащее интервалу 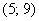 равна:
равна:
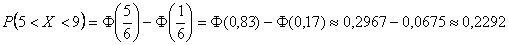
Значения функции Лапласа находятся по таблице.
Непосредственное интегрирование в системе Maple дает более точный результат:


4. (268) Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью р
= 0,6. Опыт повторяют в неизменных условиях п
раз. Сколько раз надо провести этот опыт, чтобы с вероятностью большей, чем 0,9 можно было ожидать отклонения относительной частоты появления события А от вероятности р
= 0,6 не более, чем 0,05?
Поскольку условия опыта неизменны, то применяется схема независимых испытаний Бернулли.
Используется формула: 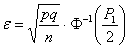
В этой формуле:
e = 0,05 – заданная величина отклонения относительной частоты от вероятности.
p = 0,6 – вероятность появления события А в одном опыте.
q = 1 – p = 0,4 – вероятность непоявления события А в одном опыте.
P1
= 0,9 – граница заданной вероятности появления А в п
опытах.
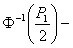 аргумент функции Лапласа для значения
аргумент функции Лапласа для значения 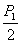
Получаем:

Ответ: для выполнения условий задачи опыт требуется выполнить 258 раз.
5. (298) В результате 10 независимых измерений некоторой случайной величины Х, выполненных с одинаковой точностью, получены опытные данные, приведенные в таблице.
| X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
X8
|
X9
|
X10
|
| 6,9
|
7,3
|
7,1
|
9,5
|
9,7
|
7,9
|
7,6
|
9,1
|
6,6
|
9,9
|
Решение:
Фактически требуется построить доверительный интервал для оценки математического ожидания а
при неизвестном значении среднеквадратического отклонения из нормально распределенной генеральной совокупности.
Требуется отыскать такое число  , для которого верно равенство
, для которого верно равенство

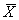 - выборочное среднее
- выборочное среднее
S
- стандартное (среднеквадратическое) отклонение
a
- математическое ожидание
n
- объем выборки (нашем случае 10)
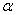 - величина, в сумме с доверительной вероятностью дающая 1
- величина, в сумме с доверительной вероятностью дающая 1
(в нашем случае 0,05)
Величину  (в нашем случае
(в нашем случае 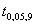 ) находим по таблицам распределения Стьюдента. Она равна 2,262.
) находим по таблицам распределения Стьюдента. Она равна 2,262.
Находим выборочное среднее как среднее арифметическое 
Рассчитаем среднеквадратическое отклонение через исправленную выборочную дисперсию:
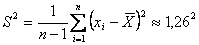
Тогда 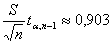
Получаем: 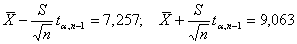
Ответ
: истинное значение случайной величины лежит в доверительном интервале (7,257; 9,063) с доверительной вероятностью
0,95.
Ниже представлен расчет данной задачи в системе Maple7.
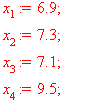  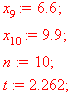 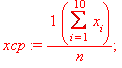  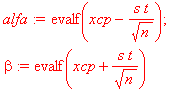
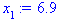  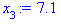 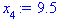 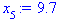
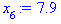 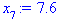 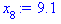 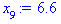 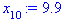
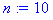 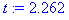
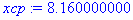
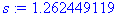
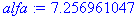
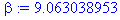
6. (308) Отдел технического контроля проверил п
= 500 партий однотипных изделий и установил, что число Х нестандартных деталей в одной партии имеет эмпирическое распределение, приведенное в таблице.
| хi
|
0
|
1
|
2
|
3
|
4
|
5
|
| ni
|
194
|
186
|
88
|
26
|
5
|
1
|
x
– число нестандартных изделий в одной партии,
n
– количество партий, содержащих х
нестандартных изделий.
Находим выборочную среднюю 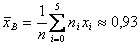
В качестве оценки параметра l распределения Пуассона 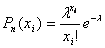 выберем полученное значение выборочного среднего
выберем полученное значение выборочного среднего 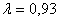 .
.
Расчет теоретических частот ведем по формуле 
Ниже представлена расчетная таблица значений.

Прим
. таблица
Microsoft
Excel. Параметры рассчитаны автоматически.
Малочисленные частоты 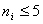 можно объединить. Также объединяются и соответствующие им теоретические частоты.
можно объединить. Также объединяются и соответствующие им теоретические частоты.
Получили: 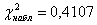
Число степеней свободы k =
s –
r – 1,
т.к. проверяется гипотеза о распределении Пуассона (т.е. проверяется один параметр), то r = 1,
k =
s – 2 = 3 (
s = 5
, т.к.
после исключения малочисленных частот в таблице осталось 5 строк)
По таблице получаем: 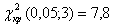
Ответ: поскольку
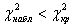 , гипотеза о том, что случайная величина распределена по закону Пуассона может быть принята.
, гипотеза о том, что случайная величина распределена по закону Пуассона может быть принята.
|