Контрольная работа: Системы с отрицательной обратной связью

ВВЕДЕНИЕ

Теория хаоса определяется как учение о сложных нелинейных динамических системах. Под термином сложные это и понимается, а под термином нелинейные понимается рекурсия и алгоритмы из высшей математики, и, наконец, динамические — означает непостоянные и непериодические. Таким образом, теория хаоса - это учение о постоянно изменяющихся сложных системах, основанное не математических концепциях рекурсии, в форме ли рекурсивного процесса или набора дифференциальных уравнений, моделирующих физическую систему.

Наиболее часто встречающееся несоответствие состоит в том, что люди полагают, что теория хаоса — это теория о беспорядке. Ничто не могло бы быть так далеко от истины! Это не опровержение детерминизма и не утверждение о том, что упорядоченные системы невозможны; это не отрицание экспериментальных подтверждений и не заявление о бесполезности сложных систем. Хаос в теории хаоса и есть порядок — и даже не просто порядок, а сущность порядка.

Это, правда, что теория хаоса утверждает, что небольшие изменения могут породить огромные последствия. Но одной из центральных концепций в теории является невозможность точного предсказания состояния системы. В общем, задача моделирования общего поведения системы вполне выполнима, даже проста. Таким образом, теория хаоса сосредотачивает усилия не на беспорядке системы — наследственной непредсказуемости системы — а на унаследованном ей порядке — общем в поведении похожих систем.

Теория хаоса говорит, что сложные нелинейные системы являются наследственно непредсказуемыми, но, в то же время, теория хаоса утверждает, что способ выражения таких непредсказуемых систем оказывается верным не в точных равенствах, а в представлениях поведения системы — в графиках странных аттракторов или во фракталах. Таким образом, теория хаоса, о которой многие думают как о непредсказуемости, оказывается, в то же время, наукой о предсказуемости даже в наиболее нестабильных системах

Однако согласно вышесказанному не следует, что теория хаоса не имеет приложений в реальной жизни. Техники теории хаоса использовались для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех, что можно себе представить. Системы динамических равенств использовались для моделирования всего — от роста популяций и эпидемий до аритмических сердцебиений.

ТЕОРИТИЧКСКАЯ ЧАСТЬ

Системы с отрицательной обратной связью

Те, кто живет в умеренном климате, знакомы с цикличностью функционирования отопительных систем. В простейшем случае имеется термостат с нагревательным элементом, находящимся на некотором расстоянии. Нагревательный элемент либо выключен, либо включен в зависимости от того, превышает ли температура некоторое значение, называемоеустановкой, или ниже него. После того, как температура упадет ниже заданной, нагреватель активируется, но из-за некоторый конечный период времени прежде чем температура в термостате превысит установку. Как только это случится, нагревательный элемент выключится, но обычно наблюдается выброс (перерегуляция) температуры до тех пор, пока тепло, выделяемое нагревательным элементом, не рассеется.

Легко видеть, что эта система функционирует циклично и что период колебаний уве­личивается при увеличении расстояния от нагревательного эле­мента до датчика температуры (порождающего временную за­держку).

С теоретической точки зрения простые механизмы с обратной связью имеют фундаментальное значение для регулирования боль­шого числа различных физиологических процессов. Нейронные се­ти с отрицательной обратной связью могут также лежать в основе механизма генераторов центрального типа (ГЦТ). Для начала рассмотрим простое дифференциальное уравнение:

(1)

где x-регулируемая переменная, а λ и γ - параметры. Так как dx/dt>0 при x<λ/γ и dx/dt<0 при x>λ/γ, эту систему можно рассматривать как простую систему автоматического регулирования с установкой λ/γ.

В физиологических системах временные задержки часто имеют важное значение, и λ и γ не являются постоянными, а регулируются механизмами с обратной связью. Чтобы построить модель таких систем, допустим, что λ и γ- соответствующие функции от x(t) и x(t-ι). Здесь ι есть временная задержка, используемая для аппроксимации временных задержек, существующих в физиологических системах.

Системы с отрицательной обратной связью — это такие си­стемы, в которых отклонения переменной состояния от стацио­нарного значения сводятся к минимуму с помощью обратной связи. В результате этого переменная состояния либо прибли­жается к своему стационарному значению, либо при некоторых обстоятельствах возникают колебания.

Рассмотрим простую модель регулирования вентиляции легких уровнем СО₂ в крови. Пусть х обозначает рС0₂ , парциальное давление С0₂ . С0₂ удаляется из организма путем вентиляции и образуется в тканях организма с постоянной скоростью λ при постоянных условиях. Вентиляция V есть монотонно возрастаю­щая функция артериального уровня СО₂ в некоторый момент вре­мени ι в прошлом. Эта задержка обусловлена временем прохождения крови от ствола мозга (где вентиляция определяется хеморецепторами и «дыхательным осциллятором») к легким (где происходит удаление СО₂ ). Для расчетов положим

(2)

где Vm -максимальная вентиляция, а θ и n – параметры, используемые для описания кривой «чувствительности» к СО₂ .Допустим также, что скорость удаления СО₂ путем вентиляции пропорциональна произведению рС0₂ на V . Учитывая оба эти фактора, получаем

(3)

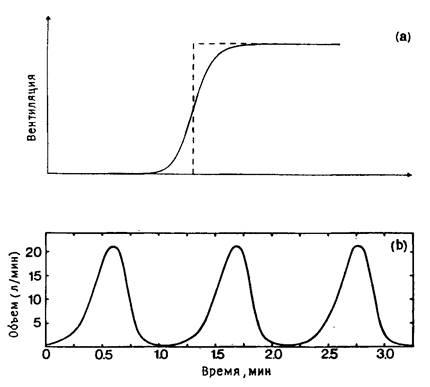
Рисунок 1. (а) Вид функции, описывающей регуляцию легочной вентиляции. (б) Колебательное решение, полученное интегрированием уравнения (3) для значений параметров, при которых вентиляция имеет колебательный характер из-за неустойчивости в петле регуляции отрицательной обратной связи. (с) Вентиляция при дыхании Чейна-Стокса.

Это пример системы с отрицательной обратной связью, так как увеличение (уменьшение) уровня артериального СО₂ приводит к увеличению (уменьшению) вентиляции, что в свою очередь при­водит к уменьшению (увеличению) уровня артериального С0₂ .

В стационарном состоянииdx/dt-0 . Обозначим значения х и V в стационарном состоянии через х* и V* соответственно и положимS*= dV/dx. Из литературы находим следующие экспериментальные значения этих параметров в стационарном состоянии:

(4)

В математическом приложении мы показываем, как может быть определена устойчивость стационарного состояния в дифферен­циальном уравнении с временной задержкой. Из представленного анализа следует приближенная оценка, согласно которой стацио­нарное состояние будет устойчивым при условии, что

(5)

Анализ также показывает, что как только стационарное состояние становится неустойчивым, при значениях параметров (4) возни­кают колебания рС0₂ (и, следовательно, вентиляции) с периодом, примерно равным 4π (рисунок 1с).

Уравнение (5) предсказывает, что стационарный уровень рС0₂ и х* может дестабилизироваться следующим образом: если крутизна S * функции регуляции СО₂ в стационарном состоянии, временная задержка τ или скорость продукции СО₂ во всем организме значительно увеличиваются, стационарное состояние становится неустойчивым; если стационарная вентиля­ция V* достаточно сильно уменьшается, это также может вызвать дестабилизацию стационарного состояния, что приводит к колеба­ниям с периодом, примерно равным 4π. Этот тип перехода от устой­чивого стационарного состояния к колебательному состоянию называетсябифуркацией Хопфа .

Эти наблюдения представляют интерес при рассмотрении типа дыхания, известного под названием дыхания Чейна-Стокса (рисунок 1с), при котором происходит регулярное увеличение и уменьшение вентиляции.ДыханиеЧейна-Стокса часто возни­кает в патологических условиях при перегрузке сердца (связанной с увеличением времени циркуляции крови от легких к хемочувствительным центрам в стволе мозга, регулирующим вентиляцию) у тучных людей (увеличенное τ) и наблюдалось также после по­вреждения нейронов ствола мозга (связано с повышенной чувстви­тельностью вентиляции к СО₂ , т. е. с увеличениемS*). Дыхание Чейна-Стокса вызывалось у нормальных собак искусственным удлинением артерий, что приводило к увеличению времени цир­куляции.

У здоровых людей дыхание Чейна-Стокса возникает на боль­шой высоте, особенно во время сна. Это явление служит причиной часто наблюдаемой неспособности к здоровому сну во время первых нескольких ночей после восхождения на большую высоту. Считается, что при таких обстоятельствах имеют существенное значение как концентрация кислорода, так и концентрация СО₂ в крови. Низкое содержание кислорода в крови стимулирует гипервентиляцию, что приводит к снижению СО₂ до нижней асимптоты кривой чувствительности к С0₂ . Вентиляция затем резко падает или вообще прекращается, пока либо увеличение С0₂ , либо уменьше­ние кислорода не приведет к ее возобновлению.

Другой пример отрицательной обратной связи дают исследо­вания системы регуляции сокращений зрачка:

Рисунок 2. (а) Иллюстрация метода, используемого для инициации колебаний диаметра зрачка. Так как свет фокусируется на границе радужной оболочки и зрачка, небольшое движение радужной оболочки приводит к большим изменениям в интенсивности света. (б) Пример спонтанных колебаний площади зрачка, полученных с помощью устройства, показанного на рисунке (а) при постоянной интенсивности света.

Небольшое пятно света направляется на край зрачка и стабилизируется таким образом, что оно всегда попадает на одно и то же место глаза (рисунок 2а). В ответ на воздействие пятнышком света зрачок сокращается. Поскольку свет больше не проникает в глаз, зрачок рефлекторно расширяется. Теперь свет снова попадает в глаз, что приводит к сокращению зрачка. Вследствие наличия времен­ных задержек в проведении нервного импульса и нелинейности петли обратной связи в системе возникают спонтанные колебания, которые могут принимать регулярный волновой характер, как показано на рисунке 2б.

Другие примеры, в которых системы регулирования обратной связью с временными задержками анализируются для выяснения механизмов периодических физиологических ритмов, могут быть найдены в гематологии, регулировании двигательной активности, психиатрии и в регулировании кровяного давления.

ПРАКТИЧЕСКАЯ ЧАСТЬ

1. Создал модель нормальной вентиляции легких (рисунок 3) по следующим формулам:

(6),

(7),

(8),

где были использованы заданные параметры нормальной вентиляции:

n =10

Для того чтобы рассчитать нужно использовать , при подсчете используем .

2. По формулам 6,7,8 построил модель вентиляции при дыхании Чейна-Стокса (рисунок 4) по следующим параметрам:

n =12

3. Построил фазовые портреты при нормальной вентиляции легких и при дыхании Чейна-Стокса (рисунки 5 и 6).

4. Построил бифуркационные диаграммы при n и (рисунки 7 и 8).

Рисунок 3. Модель нормальной вентиляции легких.

Рисунок 4. Модель дыхания Чейна-Стокса.

Рисунок 5. Фазовый портрет при нормальной вентиляции легких.

Рисунок 6. Фазовый портрет при дыхании Чейна-Стокса.

Рисунок 7. Бифуркация при изменяющемся параметре

Рисунок 8. Бифуркация при изменяющемся параметре n .

ЗАКЛЮЧЕНИЕ

В данной работе были созданы модель процесса нормальной вентиляции легких и модель дыхания Чейна-Стокса, относящиеся к системам с отрицательной обратной связью, с использованием средств MSExcel по заданным параметрам. Построены: графики, отражающие функционирование данных моделей, фазовые портреты и бифуркационные диаграммы.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Гласс Л., Мэки М. От часов к хаосу: Ритмы жизни: Пер. с англ.-М.: Мир, 1991.

2. Сидорова М.А., Можакова О.А., Истомина Т.В. Моделирование биологических процессов и систем.- Пенза: ПГУ, 2003.