Сарапульский политехнический институт (филиал)
Государственного образовательного учреждения
высшего профессионального образования
«Ижевский государственный технический университет»
Кафедра КиПР
Курсовая работа
По дисциплине: Физические основы микроэлектроники.
На тему: Дислокации. Вектор Бюргерса. Влияние дислокации на свойства
конструкционных материалов.
Выполнил: Проверил:
студент гр. 471 преподаватель
Волков А.В Иванников В.П.
Сарапул, 2010
Содержание:
Введение................................................................... 1
Виды дислокации................................................... ..2
Контур и вектор Бюргерса.......................................2-3
Движение дислокации......................................... ...3-4
Плотность дислокации..............................................4
Сила, действующая на дислокации........................4-5
Энергия дислокации..................................................5
Размножение и скопление дислокации..................5-6
Дислокации Франка и дефекты упаковки................6
Дислокации и физические свойства кристаллов.....7
Зависимость прочности от наличия дислокации...7-8
Рост кристаллов..........................................................8
Дислокации и электропроводимость.......................8-9
Заключение......................................................................10
Список используемой литературы........................... 11
Введение
Теория дислокации появилась в 50-е гг. прошлого века в связи с тем, что теоретические расчеты прочности материалов значительно отличались от практических.
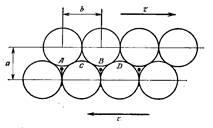
Теоретическая прочность кристалла на сдвиг впервые была вычислена Френкелем, исходя из простой модели двух рядов атомов, смещенных под действием напряжения сдвига. Межплоскостное расстояние (расстояние между рядами) равно а
, а расстояние между атомами в направлении скольжения равно b
. Под действием напряжения сдвига τ
эти ряды атомов смещаются относительно друг друга, попадая в равновесные позиции в таких точках, как А
, В
и С
, D
, где напряжение сдвига, необходимое для данной конфигурации сдвига равно нулю. В промежуточных положениях напряжение сдвига имеет конечные значения, которые периодически изменяются в объеме решетке. Предполагают, напряжение сдвига τ
будет функцией смещение х
с периодом b
:
  (1.1) (1.1)
Для малых смещений:
 (1.2) (1.2)
Используя закон Гука:
 , (1.3)
, (1.3)
где G – модуль сдвига, а  – деформация сдвига, находим коэффициент пропорциональности к
:
– деформация сдвига, находим коэффициент пропорциональности к
:
 (1.4) (1.4)
Подставляя данное значение к
в (1.1) получим:
 (1.5) (1.5)
Максимальное значение τ
, отвечающее напряжению при котором решетка переходит в неустойчивое состояние:

Можно принять а ≈
b
, тогда напряжение сдвига  . .
Вычисленные таким образом теоретические напряжения сдвига различных материалов оказалось значительно большим по сравнению с практическими значениями. Так для меди
теоретическое значение  = 760 кгс/мм, а практическое значение для реальных кристаллов = 760 кгс/мм, а практическое значение для реальных кристаллов  = 100 кгс/мм. = 100 кгс/мм.
В связи с сильным расхождением теоретических и практических результатов предположили наличие в кристалле микроскопических линейных дефектов, дислокаций.
Дислокации – нарушения непрерывности смещения между двумя частями кристалла, из которых одна претерпевает сдвиг, а другая нет. Таким образом деформация представляется последовательным прохождением дислокаций по плоскости скольжения, а не путем одновременного сдвига по всему кристаллу.
-1-
Виды дислокаций.
Различают два основных вида дислокации: краевые и винтовые.
1.Краевые дислокации.
Модель краевой дислокации можно представить прорезав в куске упруго твердого тела щель ABCD
, оканчивающуюся по линии АВ
внутри этого куска (рис.1). Материал по одну сторону сдвигается, образуется ступенька CDEF
. Линия А
B
,соответствующая концу щели, является границей между деформированным и недеформированным материалом, определяет точки выхода дислокационной линии на поверхность тела.
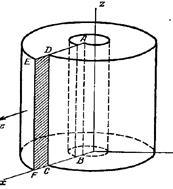 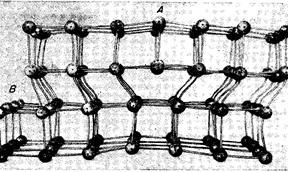
рис.1 рис.2
На рис.2 представлена наглядная модель краевой дислокации в простой кубической решетке. Краевая дислокация обусловлена наличием лишней полуплоскости А, перпендикулярной плоскости скольжения В(рис.2).
Лишняя полуплоскость может быть выше плоскости скольжения (как на рис.2) тогда дислокацию называют положительной, если полуплоскость ниже то отрицательной.
2.Винтовые дислокации:
Модель винтовой дислокации, подобна краевой, но направление сдвига винтовой параллельно линии АВ, образуется ступенька ADEF(рис3).
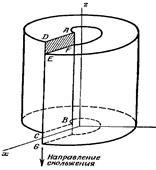 
рис.3 Модель винтовой дислокации.
Контур и вектор Бюргерса:
Для описания дислокаций в кристаллах вводится понятие о контуре и векторе Бюргерса. Контур, проведенный в совершенной решетке является замкнутым прямоугольником, в котором последний из проведенных векторов приходит в начальную точку рис.4. Контур, охватывающий дислокацию имеет разрыв, и вектор который необходимо провести для того, чтобы контур замкнулся, называется вектором Бюргерса, а проведенный контур контуром Бюргерса. Вектор Бюргерса определяет величину и направления разрыва, обычно он равен одному межатомному расстоянию и постоянен вдоль всей длины дислокации, независимо от того, меняется ли её направление или расположение. В совершенном кристалле вектор Бюргерса равен нулю. В кристалле с краевой дислокации он параллелен направлению скольжения и соответствует вектору скольжения рис.5. В кристалле с винтовой дислокацией он перпендикулярен плоскости скольжения рис.6
-2-
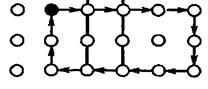 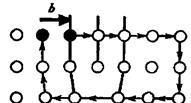 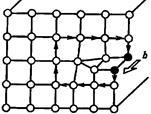
рис.4 рис.5 рис.6
В кристалле возможны и такие дислокации, которые полностью лежат внутри кристалла, а не выходят на его поверхность как у выше рассмотренных. Дислокации внутри кристалла могут прерываться на других дислокациях, на границах зерен и других поверхностях раздела. Поэтому внутри кристалла возможны дислокационные петли или взаимосвязанные сетки дислокаций. Такая дислокация может быть отделена от недеформированной области дислокационной линией в форме кольца или петли, в частности может быть получена путем вдавливания в кристалл тела. На рис.7 показано формирование призматической дислокации путем вдавливания по площади АВСD.
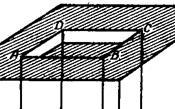 При этом формируется краевая и винтовая дислокация вектор Бюргерса, которой является векторной суммой составляющих дислокации: При этом формируется краевая и винтовая дислокация вектор Бюргерса, которой является векторной суммой составляющих дислокации:
 (1.6) (1.6)
В точке, в которой три дислокации соединяются вместе, их рис.7 векторы Бюргерса связаны соотношением:
 (1.7) (1.7)
Движение дислокации.
Важным свойством дислокаций является способность их к движению под действием механических напряжений. Пусть элементарный отрезок dl смешанной дислокации с вектором Бюргерса b движется в направлении dz. Объем, построенный на этих трех векторах:
dV = (dz×dl)·b, (1.8)
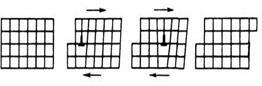
эквивалентен объему материала, перемещающегося в кристалле при движении дислокации. Если V=0, движение дислокации не сопровождается переносом массы или изменением объема кристалла. Это и есть консервативное движение, или скольжение. Для краевых и смешанных дислокаций, у которых вектор Бюргерса b не параллелен линии дислокаций dl, скольжение происходит в плоскости, определяемой векторами b и dl: выражение (1.8) равно нулю, если dz лежит в одной плоскости с векторами b и dl. Очевидно, плоскость скольжения краевой или смешанной дислокации есть та плоскость, в которой лежат дислокация и ее вектор Бюргерса. Краевая дислокация исключительно подвижна в собственной плоскости скольжения. Движение краевой дислокации может быть представлено как последовательное постепенное перемещение атомов, прилегающих по всей длине к дислокационной линии, сопровождающееся перераспределением связей между этими атомами. После каждого такого акта дислокация перемещается на одно межатомное расстояние. При этом напряжение, вызывающее движение дислокаций, значительно меньше, чем напряжение сдвига материала. В результате такого движения дислокация может достигнуть поверхности кристалла и исчезнуть. Таким образом, области кристалла, отделенные плоскостью скольжения, после выхода дислокации окажутся сдвинутыми на одно межатомное расстояние рис.8.
-3-
Консервативное движение дислокаций определяет макроскопическое скольжение в кристалле. Это самый легкий способ перемещения дислокаций в кристаллах, не обладающих жесткими и направленными связями (металлы, ионные кристаллы). Поэтому эти кристаллы легко деформируются путем скольжения. В кристаллах с ковалентными связями (полупроводники) скольжение затруднено и наблюдается лишь при повышенных температурах. Движение смешанной или краевой дислокации во всех плоскостях, кроме плоскости скольжения, должно быть связано с переносом массы, так как dV≠0. Например, краевая дислокация может двигаться в плоскости, несовпадающей с плоскостью скольжения, только если лишняя полуплоскость укорачивается или удлиняется, данный процесс называется переползанием. Процесс переползания дислокации, т. е. движения краевой дислокации не в плоскости скольжения, т.е не консервативное движение, оно связано с массопереносом или с изменением объема кристалла и возможно лишь при повышенных температурах. Переползание дислокации обусловлено диффузионными процессами движения вакансии или внедренных атомов в объеме материала. Переползание краевой дислокации, сопровождается изменением числа точечных дефектов в кристалле рис.9. ,образованием или исчезновением вакансий и межузельных атомов.
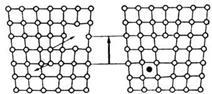
рис.9
Для винтовой дислокации, у которой b||dl выражение (1.8) равно нулю при любом направлении dz, т. е. движение винтовой дислокации всегда консервативно. Иначе говоря, это всегда скольжение, но плоскость скольжения неопределенна; плоскостью скольжения винтовой дислокации может быть любая из плоскостей зоны, осью которой служит линия винтовой дислокации. Диффузионное переползание винтовых дислокаций невозможно.
Движение дислокации обусловлено пластической деформацией кристалла. В свою очередь, причиной деформации являются внешние силы, создающие в кристалле напряжения и вызывающие движение дислокаций.
Плотность дислокации.
Согласно строгому определению, плотность дислокаций — это суммарная протяженность линий дислокаций в единице объема кристалла. Однако с достаточной точностью можно считать, что число линий дислокаций, пересекающих единицу поверхности кристалла, равно плотности дислокаций. Плотность дислокаций — важнейшая техническая характеристика качества кристалла. В кристаллах, выращенных обычными методами кристаллизации из расплава, плотность дислокаций составляет 104
- 106
см-2
. Путем отжига можно понизить эту плотность до 103
- 104
см-2
. В результате пластической деформации плотность дислокаций быстро возрастает на несколько порядков. Наилучшие полупроводниковые кристаллы, полученные путем выращивания, имеют плотность дислокаций 102
- 103
см-2
и даже порядка нескольких единиц на квадратный сантиметр, выращиваются и бездислокационные кристаллы.
Сила, действующая на дислокации.
Если на плоскость скольжения действует сдвиговое напряжение τ, то на единицу длины линии дислокации действует сила
f = τb. (1.9)
Таким образом, в области дислокации имеется локальная концентрация напряжений, тем большая, чем больше вектор Бюргерса дислокации. Представление о дислокациях объясняет особенности пластической деформации кристаллов. Плоскости и направления
-4-
скольжения — это плоскости и направления движения дислокаций. Критическое скалывающее напряжение — это напряжение, которое должна преодолеть дислокация, чтобы прийти в движение. Идеальный кристалл мог бы начать деформироваться только при одновременном разрушении всех связей в какой-либо кристаллографической плоскости. Деформация реального кристалла начинается, когда внешнее напряжение достигает значения, необходимого для начала движения дислокации, т. е. для разрыва одной или немногих атомных связей рядом с дислокацией. Поэтому прочность реальных кристаллов намного меньше, чем теоретическая прочность, вычисляемая в предположении об идеальном, не имеющем дефектов кристалле. Скорость пластической деформации зависит от скорости перемещения единичных дислокаций, от их векторов Бюргерса и плотности дислокаций. Экспериментальные данные показывают, что дислокации могут двигаться с различными скоростями — от 10-7
до 0,1 см/с в зависимости от материала, приложенного напряжения и температуры. Скорость дислокации в кристалле не может быть больше, чем скорость звука, потому что перемещение дислокации — это и есть перемещение волны упругой деформации.
Энергия дислокации.
Энергия дислокации — это дополнительная энергия, затрачиваемая на искажение решетки при образовании дислокации. Эту энергию рассчитывают как работу, которую нужно затратить против сил связи в решетке, что бы осуществить разрыв и сдвинуть две атомные плоскости в решетке друг относительно друга на вектор Бюргерса b, т. е. ввести дислокацию. Упругая энергия дислокации пропорциональна модулю сдвига кристалла и степени искажения решетки, характеризуемой вектором Бюргерса. Величина этой энергии на единицу длины линии дислокации:
U ≈ Gb2, (1.10)
где G — модуль сдвига, b — модуль вектора Бюргерса. Порядок величины U составляет несколько электрон-вольт на атомную плоскость. Дислокации с наименьшими векторами Бюргерса обладают наименьшей энергией; они наиболее устойчивы механически и наиболее подвижны. Дислокации с большими векторами Бюргерса механически неустойчивы и легко распадаются на дислокации с меньшими векторами Бюргерса.
Размножение и скопление дислокации.
Если бы новые Д. не рождались в кристалле, то пластич. деформация прекратилась бы после выхода на поверхность тела всех подвижных Д. При повышении внешних напряжений интенсивность размножения Д. увеличивается. Объяснение данного процесса впервые было предложено Франком и Ридом. Они рассматривали дислокацию призматического типа, образованной путем сдвига части кристалла от ABC к DEF, причем DEF представляет при этих условиях дислокационную линию. Если сдвиговое напряжение приложено к плоскости скольжения ABED и на части дислокационной линии EF действие силы не проявляется, то данная дислокация рассматривается как неподвижная, или сидячая. Но на дислокацию действует сила и она будет продвигаться вперед. Так как дислокация ED закреплена в точке Е, она будет поворачиваться вокруг этой точки, поскольку приложенное напряжение стремится расширить площадь области, охваченной сдвигом рис.10.
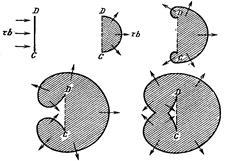 
рис.10
-5-
Если на плоскости дислокации имеется препятствие, то дислокации скапливаются у этого барьера рис.11. Последние дислокации оказывают давления на первые, в результате чего расстояние между ближайшими к препятствию дислокациями оказывается значительно меньшим, чем между последними и возникает равновесное распределение.
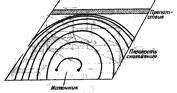
рис.11
Расщепление дислокации в плотно упакованных структурах.
В рассмотренных выше моделях простой кубической решетки смещение на величину одного вектора Бюргерса соответствует той же конфигурации, что и до смешения. Такая дислокация называется совершенной или полной. Если же движение атомов приводит к новому расположению атомов, то дислокация называется несовершенной, или частичной (Дислокация Шокли). Преобладающий в данном кристалле тип дислокации в какой-то степени определяется его структурой, но существует также энергетический критерий, который нужно учитывать. Полные дислокации, вектор Бюргерса которых больше межатомного расстояния, нестабильны и могут расщепляться на две или более частичных, если в результате этого энергия системы понижается.
Правило Франка гласит, что энергия деформации дислокации пропорциональна квадрату вектора Бюргерса, и если сумма квадратов вектора Бюргерса компонент, на которые распадается дислокация, меньше чем квадрат вектора Бюргерса первоначальной дислокации, то происходит расщепление.
Дислокации Франка и дефекты упаковки.
Частичная дислокация Франка образуется в структуре с порядком расположения плотно упакованных плоскостей типа гранецентрированного куба либо путем удаления части одной из плотно упакованных плоскостей, либо при вставлении лишнего участка такой плоскости. В первом случае образуется отрицательная частичная дислокация Франка рис12, во втором положительная, дислокация Франка которая имеет краевой характер. Дислокации Франка не могут перемещаться по плоскости скольжения.
Отрицательная дислокация Франка при удалении слоя А приводит к возникновению следующего дефекта упаковки: АВСВСА, который называется дефектом вычитания. В случае положительной дислокации добавляется слой В: АВСВАВС - дефект внедрения.
В гранецентрированной кубической решетке атомы расположены в порядке АВСАВСАВС, так что каждый четвертый слой находится в такой же позиции, что и первый. Но из-за наличия дислокации возможно АВСАСАВСА, последовательность САСА отвечает гексагональной структуре, такие изменения расположения атомов называется дефектом упаковки. На рис.13 изображено нормальное расположение атомов, а на рис.14 с дефектом упаковки.
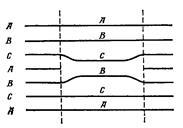 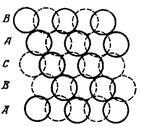 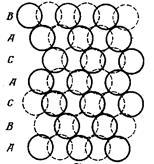
рис.12 рис.13 рис.14
-6-
Дислокации и физические свойства кристаллов.
Д. влияют в первую очередь на механические свойства твёрдых тел, для которых их присутствие часто является определяющим. Д. изменяют оптические свойства кристаллов, на чём основан метод наблюдения изолированных Д. в прозрачных материалах.
Нарушение регулярности кристаллической решётки в ядре Д. приводит к тому, что в местах выхода линий Д. на внешнюю поверхность тела химическая стойкость кристалла ослабляется и специальные реагенты способны разрушать окрестность оси Д. В результате обработки поверхности кристалла таким травителем в местах выхода Д. образуются видимые ямки (дислокации впервые наблюдались именно по ямкам травления). Д. косвенно влияют на свойства кристаллов, зависящие от характера распределения и перемещения в них точечных дефектов (примесей, вакансий, центров окраски и др.). Во-первых, при определ. характере движения Д. испускает или поглощает вакансии, изменяя их общее кол-во в кристалле. Динамическое образование заряженных вакансий в ионных кристаллах и полупроводниках может сопровождаться люминесценцией. Также Д. влияют на скорость диффузионного перемещения точечных дефектов, вдоль оси Д., как правило, больше, чем скорость их диффузии через объём регулярного кристалла(Д. играют роль своеобразных "дренажных труб", по которым точечные дефекты довольно легко могут перемещаться на большие расстояния в кристалле). Взаимодействие Д. с точечными дефектами (примесными атомами и вакансиями) приводит к повышению концентрации последних вблизи оси Д. и образованию вокруг неё так называемых. облаков Котрелла. Сгущение атмосферы Котрелла в перенасыщенных твёрдых растворах может привести к коагуляции примесей на Д. В прозрачных кристаллах это приводит к "декорированию" Д., что делает их визуально наблюдаемыми. Осевшие на Д. примеси блокируют её движение. В распадающихся сплавах Д. взаимодействует с макроскопическими включениями новой фазы.
Зависимость прочности от наличия дислокации.
На рис.15 изображена типичная зависимость механического напряжения от относительного удлинения при растяжении образца. Кривая имеет 3 характерных участка. Участок 0-1 соответствует упругим обратимым деформациям, когда выполняется закон Гука. Участок 1-2 соответствует необратимым пластическим деформациям. Участок 2-3 соответствует разрушению образца.

рис.15
Величину , отвечающую точке 1, называют пределом текучести, а отвечающую точке 2, называют пределом прочности. Попытки рассчитать предел текучести без учета дислокаций приводили к завышенным на 2-4 порядка значениям.
Предел текучести материала сильно зависит от плотности дислокаций в нем. На рис. 16 приведена такая зависимость. Видно, что предел текучести оказывается больше при очень малых значениях плотности дислокаций и, наоборот, при больших плотностях дислокаций. Увеличение при больших связывают с взаимодействием дислокаций друг с другом и с другими дефектами кристаллической решетки.
-7-
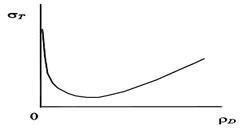
Рис. 16.
Схематическая зависимость предела текучести от плотности дислокаций
Пути увеличения прочности материалов. В настоящее время используют ряд способов увеличения прочности материалов, позволяющие достигать предела прочности порядка 0.01; большинство из них связаны с введением дополнительных препятствий движению дислокаций. Такими препятствиями являются различные дефекты: 1) выделения другой фазы ; 2) точечные дефекты и их скопления; 3) большие количества дислокаций, тормозящие движение дислокаций за счет взаимодействия друг с другом; 4) ближний порядок в расположении атомов.
Во многих сплавах наблюдается явление, называемое ближним порядком, когда атом одного сорта стремится окружить себя преимущественно атомами другого сорта, при этом достигается меньшая энергия сплава. При движении дислокации разрываются более энергетически выгодные, а формируются менее выгодные связи между атомами. На это требуется большая энергия, что приводит к увеличению усилий, необходимых для смещения дислокации и, в конечном счете, к увеличению прочности материала.
Перечисленные способы хотя и значительно увеличивают прочность, но и, как правило, сильно уменьшают пластичность материала. Прочность кристаллов может быть больше и при особо малой плотности дислокаций, когда затруднена деформация кристалла по дислокационному механизму. Снижение температуры также препятствует свободному перемещению дислокаций. При низких температурах прочность растет, а пластичность падает. Металл становится более прочным, но хрупким.
Повышение прочности металлов и сплавов может быть достигнуто двумя путями:
1) Получением металлов с близким к идеальному строением кристаллической решетки, т. е. металлов, в которых отсутствуют дефекты кристаллического строения или же их число крайне мал. 2) Либо, наоборот, увеличением числа структурных несовершенств, препятствующих движению дислокаций (в основе данного метода чаще упрочняют металлы).
 Рост кристаллов. Рост кристаллов.
Д. играют важную роль при росте кристаллов из парообразного и жидкого состояний. Было установлено, что в действительности кристаллы растут гораздо быстрее, чем можно было бы ожидать в случае совершенных кристаллах при малых насыщениях. Трудность в объяснении данного процесса была преодолена путем введение в рассмотрение винтовой дислокации, выходящей на грань кристалла и создающую непрерывную самовозобновляющуюся ступеньку. рис.17
Таким образом кристалл представляет одну сильно закрученную спираль рис.17, где представлена спираль роста в карбиде кремния.
Дислокации и электропроводимость:
Наличие дислокаций в кристалле существенно сказывается не только па механических свойствах, но и на электрических характеристиках материала. В частности Д. может нести или захватывать электрический заряд и обладать намагниченностью, отличной от
-8-
намагниченности кристалла. Наличие Д. повышает электросопротивление проводников и изменяет концентрацию свободных носителей заряда в полупроводниках. Дислокации могут являться источником большого числа носителей заряда, а также центром рекомбинаций и рассеяния носителей.
Так введение дислокаций в кристалл полупроводника из германия(p-Ge), уменьшает количество дырок проводимости уменьшается, и чем больше дислокаций, тем сильнее оно уменьшается. В то же время температурная зависимость меняется незначительно, то есть энергия электронов, захваченных дислокацией, слабо зависит от температуры (рис.18). Возникает кулоновская блокада: если дислокация захватила электрон, то на соседнюю оборванную связь электрону устроиться гораздо труднее, потому что существует кулоновское отталкивание между двумя электронами. При введении дислокаций в кристалл n-Ge количество электронов проводимости наблюдается такая же зависимость как и в кристалле p-Ge. На рис.19 изображен график зависимости концентрации электронов при различном расположении дислокации относительно магнитного потока.
-9-
Заключение
Наличие дислокаций в кристалле существенно сказывается свойствах, характеристиках материала. Без учета этих дефектов невозможно уже представить многие области науки, связанные с кристаллами. Теория дислокации широко применяется нетолько в материаловедении, но и в микроэлектролнике. И наряду с микронеоднородностью распределения примесей существование дислокаций является серьезным фактором, сдерживающим микроминиатюризацию интегральных элементов. Поэтому ведутся исследования по получению малобездислакационных кристаллов и на сегодняйший день удается получить практически бездислокационные кристаллы при выращивании их в условиях, свободных от физических напряжений, и при предельно малых температурных градиентах. В настоящее время в промышленных условиях изготавливаются малодислокационные полупроводниковые кристаллы с плотностью дислокаций порядка 102
см2
.
-10-
Список используемой литературы:
Р.Хоникомб Пластическая деформация металлов. Перевод с английского.
Фридель Дислокации
Рид Дислокации в кристаллах
Осипьян Ю.А. Взаимодействие электронов с дислокациями в кристалле.
-11-
|